复杂多态系统的冗余备份元件优化①

付 林, 史小宏

(上海海事大学 信息工程学院, 上海 201306)

复杂多态系统的冗余备份元件优化①

付 林, 史小宏

(上海海事大学 信息工程学院, 上海 201306)

在复杂的多态系统中, 系统可靠性非常重要, 最常见的是冷热备份模式来实现系统的可靠性. 本文中我们提出了混合冗余备份模式, 计算复杂系统的可靠性和任务成本, 解决复杂系统中的备份元件优化分布和初始化问题. 本文主要是通过离散数学的概率分布计算复杂系统中元件的可靠性和任务成本, 利用量子遗传算法来解决冗余备份元件的优化分布问题. 最后同时通过仿真实验来计算出系统的可靠性和预期的任务成本,以及冗余备分元件的优化分布, 得出了复杂系统可靠性与成本的平衡关系.

冗余备份; 冷热备份; 量子遗传算法; 可靠性; 任务成本

1 引言

传统类型的冗余备份主要是利用元件备份来做系统可靠性保障的[1], 这类备份只是单纯的靠元件的替换来满足可靠性要求, 而你没有考虑成本损耗问题,另外就是冷备份和热备份[2]. 这类备份模式虽然也是利用多余的元件来做备份, 不过考虑到了成本损耗问题, 没有进一步的去探讨元件的优化分对于系统可靠性和成本的影响. 元件处于热冗余备份模式下的时候,当有运行操作的元件故障的时候, 可以快速的替换掉故障元件, 从而提供快速恢复, 为了保证能够随时替换出故障的运行操作元件, 就需要时刻补充处于热备份模式的备用元件, 这就增加了整个系统的成本开支,相比之下, 冷备份模式下的元件, 就不会有这样的消耗, 但是冷备份元件替换故障元件的时候, 需要很长的恢复延迟时. 系统中热备份冗余相关的成本消耗和系统可靠性高于冷备份冗余元件. 因此需要在可靠性和成本之间做一个平衡[3]. 一个好的办法是可以通过在同一个系统中设计两种类型的冗余, 即让一部分备用元件处于热备份模式下, 让大多数备份元件处于冷备份模式下可以减少维护成本, 同时热冗余备份元件又可以保证一定的系统可靠性, 最后对系统的可靠性和成本的需求不同, 冷热备份模式中系统元素的分布和备用元素启动的顺序会严重影响系统的可靠性以及任务的成本[4]. 冷和热备份中元件的分布以及初始化序列的选择可以使得系统满足一定的可靠性同时成本最小化, 在本文中我们将使用可靠性和预期成本算法计算复杂系统的可靠性和预期任务成本, 利用冗余元件来满足系统可靠性的同时, 计算系统的任务成本,同时在文中我们使用量子遗传算法去优化系统中备份元件的初始化顺序, 研究冗余元件在系统中的分布不同对系统的可靠性和成本的影响, 从而在满足一定的可靠性基础上计算系统的可靠行和成本, 并找出对应的备份元素的初始化顺序.

2 元件的混合冗余备份模型

假设系统中有N个元件h( 1),h(2),...,h(N), 假定最开始的H个元件是处于热备份模式下, 因此在任务开始的时候元件h(1),h(2),...,h(H)就开始初始化了, 剩下的N-H个元件h(H+1),...,h(N)处于冷备份模式下,所有处于热备份模式下的元件在任务开始的时候就被初始化了, 当处于操作状态的元件故障后热备份模式下的一个元件就会替换掉故障的元件, 当所有热备份模式下的备用元件都替换完之后, 紧接着就将冷备份模式中的元件初始化, 如果所有元件在任务结束时间之前都故障了, 那么整个系统任务就失败了.

为了计算系统的可靠性我们做出如下假设[5]:

1) 系统中的各个元件是相互独立的

2) 在替故障元件到系统恢复这段时延跟整个任务时间相比可以忽略不计

3) 由于热备份模式下的元件压力跟操作状态下一样, 所以维护成本用操作成本来计算

4) 系统中的元件数量和类型是固定

5) 系统和元件故障是不可修复的

2.1 操作时间段内的故障元件的概率计算

我们假设系统的任务时间是t, 将任务时间t划分成m个相等的时间间隔, 每个时间间隔是Δ=t /m, 元件j在第i时间间隔故障的概率分布函数pj(i)可以通过累计故障分布函数Fj(t)来获得, 其中第i时间间隔为Δi=Δ(i+1)-Δ(i), 对应的累计分布函数为Fj(Δ(i+1))-Fj(Δi)

对于元件故障时间分布满足故障指数为λj的指数分布的时候, 则元件j的故障累积时间分布函数就可以用下面公式表示:

对应的元件j在第i时间间隔故障的概率分布函数pj(i)就可以通过对分布函数求导得到, 如下式:

对应的比例参数αj和形状参数βj的威布尔分布函数和概率密度函数为:

在我们的系统模型中元件的故障时间分布式离散的而不是连续的, 那么整个任务时间段内元件j的离散时间可以Tj就可以用向量Pj=(pj(0),...,pj(m))来表示, 其中pj(i) =Pr{Tj=Δi} 是时间间隔为Δi(0≤i≤m)的故障概率. 因为没有元件的操作时间比总的任务时间t要长, 因此元件j在时间内不出现故障的概率pj(m)=Pr{Tj≥t=Δm}, 就可以表示为

2.2 系统元件的故障时间分布计算

对于任意一组给定的元件序列h( 1),h(2),...,h(N),我假定最开始的H个元件是处于热备份模式下, 因此在任务开始的时候元件h(1),h(2),...,h(H)就开始初始化了, 剩下的N-H个元件处于冷备份模式下. 对于任意一个j＞H处于冷备份的元件在系统中j-1个元件出故障的时候开始初始化,h(j)该元件在系统中初始化的索引序列. 那么系统中第j个在任务开始到时间Xj出现故障就可以表示为向量Qj=(Qj(0),...,Qj(m)), 其中Qj(i)=Pr{Xj=Δi} . 那么元件h(1)在时间任务开始的时候初始化, 就有X1=Th(1)和Q1(i)=ph(1)(0≤i≤m). 所有的热备份下的元件都是在任务开始的时候初始化的, 因此热备份模式下的元件有Xj=max(Xj-1,Th(j)), 进而获得可靠性如下:

对于冷备份下的元件, 要等到热备份下的元件都出现故障后才会去初始化, 因此有Xj=Xj-1+Th(1),进而获得冷备份下元件的可靠性如下:

2.3 可靠性与预期任务成本计算算法

3 量子遗传算法优化元件分布与初始化序列

3.1 量子遗传算法的思想

系统的元件的分布与初始化序列优化问题是一个复杂的组合优化问题[6], 有N*N!个可能的解决方法, 要去详尽的检测每一种可能来确定一个相对最优的方法是不可能, 传统的启发式算法计算量比较复杂并且得到的解的误差比较大[7], 利用遗传算法来搜寻的时候不用去考虑下一步的搜寻方向来找到一个最优的解.

遗传算法来自于生物进化论, 通过模拟自然界的生物进化, 用编码串也就是生物进化里面的“染色体”对问题进行优化. 将问题的所有的解的集合在一起,形成一个种群, 利用选择, 交叉, 变异对种群的解进行优化, 每个染色体都对应有一个解值. 采用用遗传算法解决问题时, 需要确定以下几个要素[8,9]:

1) 通过对染色体上的基因进行编码将问题的解体现出来确定染色体的编码.

2) 将适应度高的个体遗传到下一代群体当中去建立个体的适应度函数.

3) 初始化种群.

4) 对基因进行复制, 交叉, 变异等遗传操作产生下一代群体, 确定遗传算子.

5) 确定群体规模, 终止进化代数, 交叉率pc, 变异概率pm.

量子遗传算法是将量子计算和遗传算法结合起来.对比传统的遗传算法和量子遗传算法, 研究人员发现量子遗传算法能够种群规模很小的情况下, 用很小的代价找出相关问题的最优解[10]. 量子遗传算法采用的编码方式与传统的遗传算法编码方法有很大的不同,量子遗传算法利用量子位染色体编码, 而且利用量子门来完成种群的更新, 从而产生新的最优种群[11], 这里就是找到最优的解集.

3.2 量子遗传算法的优化过程

第一步: 用量子比特表示最小的信息单元. 一个量子比特的状态可表示为在量子遗传算法中第t代染色体种群可以表示为Q(t)=[q1(t),q2(t),...,qn(t)], 其中,

第二步: 量子算子的定义, 选择算子: 采用跟遗传算法类似的轮盘赌来确定遗传算子. 变异算子: 在量子遗传算法中通过量子旋转门的旋转角来表示量子染色体中的变异操作, 下面的式子是本文用到的量子变异算子[12].

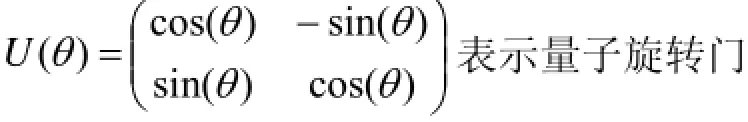
交叉算子: 在量子遗传算法中采用量子的相干性的特性进行全干扰交叉操作[13], 使得种群中的个体都能够参与到进化中而不是局部的进化. 以种群规模为5计算, 染色体的长度为5计算, 用A, B, C, D, E表示交叉后获得的新的染色体如表1所示.

表1 全干扰交叉

所谓的元素分布与优化问题就是找出一组元素初始化列, 使得在满足一定的可靠性级别R*的时候系统的成本最小[14].

对于任何染色体代表的元件的初始化顺序, 我们可以找出处于热备份模式和冷备份模式下的元件, 利用利用上面的求可靠性和任务成本的算法, 我们可以求出系统中元件处于该顺序的时候的可靠性R和预期的任务成本C, 这样的话我们再利用公式(8), 我们可以定义一个值,式中M是一个足够大的整数, 我们可以利用这个公式解决系统的优化问题, 当σ=0的时候, 就可以求出最小任务成本, 当σ比较大而R*=1的时候, 问题就转化为了求系统的最大可靠性问题. 在量子遗传算法的开始的时候用一组0到N的任意数字代表一组解决方法, 随机产生的数字代表了系统中冗余备份元件的初始化顺序, 比如2,3,5,6,1,4这组数字, 2,3,5就代表了热备份元件的初始顺序, 通过交叉和变异过程获得新的的解决方方法, 根据求解的方法来求适应度函数的值, 将得到的初始化顺序代入到2.3节的可靠性和预期任务成本算法中去, 计算这种情况下的可靠性和任务成本,带入到公式(8)中去比较求得适应度值是否满足要求,然后操作量子旋转门, 调整种群的个体, 获得新的个体保留最优解, 之道量子遗传算法跌代到求出一组初始化序列, 并且求得此时的可靠性满足公式(8), 量子遗传算法结束, 记录下得到最优解情况下的备份元件的初始化序列.

4 仿真结果与分析

4.1 模型计算结果与分析

我们可以通过一个例子来验证一下模型, 假设一个复杂系统中含有10个元件, 我们利用威布尔失效时间分布模型来描述系统中元件的故障状态, 并且在表2中给出了威布尔规模参数αj和状态参数βj. 同时在表2中给出了冷备份和热备份模式下的元件启动成本, 假设系统的任务时间是t=400, m=500的时候前五个元件处于热备份模式下, 后五个元件处于冷备份模式下, 这样我们利用上面的算法就可以计算出系统的任务成本C=22656和可靠性R=0.8109.

表2 系统中元件的各种参数

2 100 1.0 2050 5 40 15 3 150 1.1 2150 9 70 13 4 80 1.0 2000 4 50 9 5 110 1.3 2200 6 80 12 6 75 1.0 2050 5 90 10 7 120 1.0 2150 6 70 12 8 130 1.1 2080 9 70 13 9 110 1.0 2150 3 90 9 10 140 1.1 2080 4 60 8

同时为了研究不同任务时间段m对系统可靠性和成本的影响, 假设五个元件处于热备份模式下, 另外五个元件处于冷备份模式下, 我们可以通过图1看出不同任务时间段对可靠性和成本的影响.

图1 可靠性和任务成本任务随时间段m的变化

4.2 元件分布优化与初始化序列结果与分析

我们假设系统中有10个元件, 利用表2中给的参数和模型中提出的可靠性与成本计算算法, 利用量子遗传算法来优化处理, 我们可以得出系统中元件最优元素分布随着遗传代数而变化, 最优解达到一个稳定的趋势如图2所示.

图2 系统中元件的分布随着遗传代数的变化

同时我们可以求出在满足不同的可靠性R*的时候,利用量子遗传算法计算出系统的可靠性和预期任务成本以及系统中元件的初始化序列如表3所示.

表3 对于满足不同的可靠性R*得到的元件序列

最后我们可以得到不同的可靠性与预期任务成本的一个平衡曲线如图3, 根据这个图可以帮助我们来设计系统的混合冗余备份, 可以根据对成本和可靠性需求的要求来分配备份元件.

图3 可靠性和预期任务成本的平衡

5 结语

在本文中我们主要解决的是系统元件不可修复的情况, 通过对系统中冗余备份模式的分析, 提出了我们的算法, 并且通过实例来计算出了混合备份模式下系统的可靠性和预期成本, 在论文的后半部分利用量子遗传算法对系统中元件分布进行处理, 找出了在满足一定可靠性和预期成本的时候系统中元件的一组初始化序列, 通过图三直观的显示了系统可靠性跟预期成本之间的关系, 为系统元件分布和优化提供了依据.

1 祝春标.基于多部件的冗余备份计算机通信系统分析.信息与电脑:理论版,2010(5).

2 葛晶晶.基于Markov过程的网络控制系统冗余技术研究[硕士学位论文].大连:大连理工大学,2014.

3 Levitin G, Xing L, Dai Y. Cold vs. hot standby mission operation cost minimization for 1-out-of-N systems. European Journal of Operational Research, 2014, 234(1): 155–162.

4 黎湘,郁文贤,庄钊文,等.决策层信息融合的神经网络模型与算法研究.电子学报,1997,(9):117–120.

5 吴頔.不可修复如新的多状态串联系统可靠性分析[硕士学位论文].武汉:武汉科技大学,2013.

6 许传玉,朱若男,梁颖红,等.遗传算法在复杂系统可靠性优化中的应用.哈尔滨理工大学学报,2000,5(3):90–93.

7 汪松泉.遗传算法在组合优化中的应用研究[硕士学位论文].合肥:安徽大学,2010.

8 邵军,程华,徐军.遗传算法在结构可靠性优化中的应用.四川建筑科学研究,2001,27(2):4-5.

9郑世珏,陈晓燕,高丽.基于量子遗传算法的传感器节点优化部署方法.计算机工程与设计,2008,29(7):1681–1683.

10 周殊,潘炜,罗斌,等.一种基于粒子群优化方法的改进量子遗传算法及应用.电子学报,2006,34(5):897–901.

11 周传华,钱锋.基于改进量子遗传算法的小波神经网络优化及其软测量应用.华东理工大学学报:自然科学版,2008, 34(6):850–853.

12 陈晓燕.基于量子遗传算法的无线传感器网络节点定位算法研究[硕士学位论文].武汉:华中师范大学,2009.

13 杨玉,戴红伟,李存华.量子干扰交叉遗传算法及其应用研究.2011年江苏省人工智能学术会议,2011.

14 张铁柱,滕春贤,韩志刚.遗传算法在系统可靠性优化中的应用.控制与决策,2002,17(3):378–380.

Optimization of Redundant Backup Components in Complex Polymorphic System

FU Lin, SHI Xiao-Hong
(College of Information Engineering, Shanghai Maritime University, Shanghai 201306, China)

In the complex polymorphic system, system reliability is very important, and the most common mode to realize the system reliability is the cold and hot backup mode. In this paper we propose a hybrid redundant backup mode, to calculate the reliability of complex systems and task cost, and to solve the problems of optimization distribution and initialization of backup components in complex system. With the probability distribution of discrete mathematics, this paper mainly calculates the reliability and task cost of components in complex system. Then, use quantum genetic algorithm to solve the problem of redundancy backup element optimization distribution. Finally, simulation is implemented to calculate the reliability of the system, the expected task cost, and optimization distribution of redundant backup devices. It concludes the balance relationship between reliability and task cost of complex system.

redundancy backup; cold and hot backup; quantum genetic algorithm; reliability; task cost

2016-03-26;收到修改稿时间:2016-05-05

10.15888/j.cnki.csa.005497