土体蠕变作用下高桩码头变形分析方法研究
2016-02-16刘现鹏刘红彪
刘现鹏,韩 阳,刘红彪
(交通运输部天津水运工程科学研究所港口水工建筑技术国家工程实验室水工构造物检测、诊断与加固技术交通行业重点实验室,天津300456)
土体蠕变作用下高桩码头变形分析方法研究
刘现鹏,韩 阳,刘红彪
(交通运输部天津水运工程科学研究所港口水工建筑技术国家工程实验室水工构造物检测、诊断与加固技术交通行业重点实验室,天津300456)
高桩码头使用过程中,土体的弹塑性变形与蠕变变形会引起较大的结构位移,进而影响结构的使用安全。文章采用修正Drucker⁃Prager/Cap模型和Singh⁃Mitchell模型模拟土体本构关系,结合三维精细有限元理论,提出了一种分析土体变形对高桩码头结构影响的数值分析方法,并将其应用于天津港高桩码头的分析计算。结果表明,该方法可以较好地反映土体弹塑性变形与蠕变变形对结构的影响,将为土体变形对高桩码头的影响研究提供一条可行的途径。
高桩码头;土—结构相互作用;土体蠕变;有限单元法;岸坡体系
高桩码头由上部结构和支撑上部结构的桩基组成,相比于其他码头结构有着建造速度快,波浪反射小和稳定性高等优点[1],在工程中有着广泛的应用,尤其适用于软土地基环境。其桩基部分在使用过程中不仅受到堆载、靠泊力以及系缆力等荷载作用,还会受到岸坡土体对结构的挤压力和摩擦力。尤其是在软土地基环境下,这种土—结构相互作用将对结构变形产生较大影响进而影响结构安全性。天津港北港池某杂货码头在码头结构检测中发现该码头出现了大量的后承台靠近挡土墙区域的后承台横梁损伤,损伤多为横梁在桩帽节点处混凝土大面积剥落。根据混凝土结构参数检测和变形监测结果,分析该码头出现的结构损伤系土体蠕变和码头堆载共同作用所致[2]。
蠕变对天津港地区港工建筑物的影响一直是研究热点。天津大学岩土工程研究所闫澍旺等于2003年对天津港南疆港区突堤的蠕变进行了研究,通过建立蠕变模型和有限元计算对结构的变形进行了预测[3]。天津大学与2006年陈滨分析蠕变和差异沉降对桩基与土体相互作用的影响。软土蠕变、后方加载和时间的增长可以增大内力和水平位移,影响码头的正常使用[4]。天津大学王婷婷于2008年建立了滨海软粘土非线性蠕变本构模型。并将该模型应用于筒型基础防波堤的有限元计算中,取得了较好的结果[5]。交通部天津水运工程科学研究所李越松等人于2009年对天津港北疆港区高桩码头桩顶变形进行了结构与土相互作用的蠕变变形计算,结果表明,蠕变是导致桩基侧向变形重要因素[6]。天津大学丁琼对堆载作用下高桩码头进行了研究,结果表明岸坡的蠕变变形将大大增加土体的侧向变形,因而对整个排架桩基的作用效应也更加突出[7]。天津大学董焱赫于2013年对滨海地区土体蠕变模型进行了研究,并将研究成果用于天津港重力式防波堤在循环荷载和土体蠕变作用下的沉降预测,结果表明,长期循环荷载作用下软土的蠕变效应更明显[8]。
综上所述,研究土体—结构的相互作用,探讨岸坡土体蠕变对高桩码头的变形影响,对码头的结构损伤机理分析和修复加固有重要意义。本文基于有限单元法,提出了一种土体蠕变作用下码头结构变形的数值分析方法,并用于天津港高桩码头的变形计算,取得了较好的应用效果。
1土体本构关系模型
1.1剑桥模型与修正剑桥模型
剑桥模型是由英国剑桥大学的Roscoe及其合作者在大量实验测试的基础上于1963年提出一类描述土的非线性行为的本构关系模型[9]。该模型考虑了正常固结土和超固结土试样的排水和不排水试验,提出了土体临界状态的概念。传统剑桥模型采用单一屈服面(临界状态方程),其表达形式为

式中:p为静水压力;q为Mises等效应力;M为比例系数,与土体的有效摩擦角有关:v为比体积;vf为某一卸载曲线卸载到p=1 kPa时对应的比体积;λ为临界状态线斜率。
1965年,Burland对剑桥模型进行了研究,认为剑桥模型在后缘尖端存在不光滑的情况,与土试样试验结果不符,同时这种不光滑很不利于模型的数值分析和计算。经过研究,Burland对剑桥模型进行了改进,提出了修正的剑桥模型[10]。修正剑桥模型将屈服面的后半段(式中第二式)修正为椭圆的形式,表达式为

式中:pc为硬化参数。
Abaqus软件中对经典的修正剑桥模型做了进一步扩展,进一步改进了椭圆部分的表达式,考虑了应力第三不变量的影响,建立了黏土塑性(clay⁃plasticity)模型。该模型的屈服面也是直线屈服面和椭圆屈服面的结合,表达形式如下

式中:M为临界状态线在p-t平面上的斜率;a为椭圆与临界状态线交点所对应的p的大小;β为椭圆率控制参数。
剑桥类模型,包括原始剑桥模型、修正剑桥模型和黏土弹塑性模型,由于其坚实的工程背景,在岩土工程中应用非常广泛,但其中也存在一些问题:首先,剑桥类模型的极限状态线大都是原点指向的,忽略了内聚力的影响;其次,剑桥类模型一般应用于土体材料的静力分析,对于土的蠕变分析等问题,目前尚未有成熟的土体蠕变模型与剑桥类模型相配合;再则,剑桥模型与土体的孔隙等有直接关系,但是直接将土体考虑为孔隙材料将大大增加土体有限元分析的难度,此时再叠加考虑蠕变等非线性因素,极容易引起数值模拟的发散。
1.2修正的Drucker⁃Prager/Cap模型
为了克服剑桥类模型的缺点,特别是要进行土体蠕变行为的准确模拟,同时充分利用前期基于剑桥类模型所整理的试验结果,这里引入修正的Drucker⁃Prager/Cap模型。首先给出这类模型在p-t平面的屈服面,如图1所示。
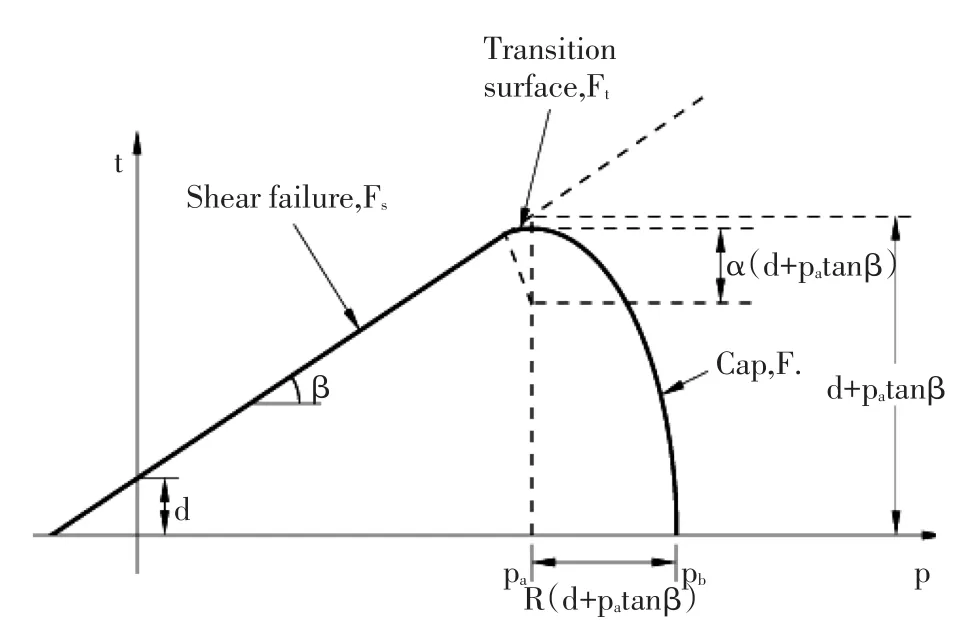
图1 修正的Drucker-Prager/Cap模型的屈服面Fig.1 Yield surface of modified Drucker-Prager/Cap model
其中左侧直线为Drucker⁃Prager屈服面,方程为

可以看出,该方程与剑桥类模型的极限状态面相比,形式十分类似,其斜率可以与剑桥类模型取相同的数值,而内聚力也可以在试验成果中查到。右侧的盖帽(Cap)模型,其表达形式为
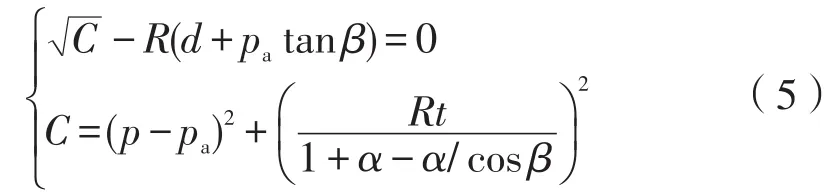
可以看出,其本质也是椭圆,与修正的剑桥模型具有一致性[11],也可以采用基于剑桥模型整理的试验成果加以逼近。修正的Drucker⁃Prager/Cap模型屈服面十分光滑,十分便于数值分析和模拟,实践证明基于此进行的数值模拟稳定性较好。另外,修正的Drucker⁃Prager/Cap模型有成熟的蠕变模型与之相配合,通用有限元软件Abaqus在此模块中提供了几类蠕变模型供数值模拟使用。
1.3蠕变模型
一般认为,材料的蠕变与材料的应力水平和时间有关。Abaqus中提供的与修正的Drucker⁃Prager/Cap模型相配合的蠕变模型分为三类:第一类是时间硬化模型,其表达形式为


这一类模型认为蠕变应变率表达式不含时间,这也与岩土材料的蠕变试验观测不符。第三类是Singh⁃ Mitchell模型,其表达形式为

虽然S⁃M模型也有一些问题,如模型对应的剪应力水平在20%~80%,超出这个范围结果不理想,根据土体蠕变试验结果和现有的软件功能,S⁃M模型不失为本课题中模拟土体长期蠕变的理想选择。
2三维有限元分析模型
目前对高桩码头与土体研究的有限元模型主要有两类,即二维模型和三维模型。二维模型由于计算简单,易于实现,被广泛采用。但是二维模型的缺点也十分明显,某些我们关心的变形模式并不能被准确表示。所以这里采用三维有限元模型。
2.1弹塑性有限元格式
从平衡方程出发,引入弱形式表达,可以建立结构有限元分析的基本表达式。考虑如下平衡方程

其中σij为应力张量,bi为体力向量。考虑应变的定义

平衡方程的变分形式如下

对于弹性材料,其本构关系可以表示为

其中为材料刚度。上式代入式(11),并考虑有限元划分和插值函数构造,可得结构方程

其中u为位移向量,刚度矩阵

外力向量

对于线弹性材料,方程(13)为线性方程,直接求解就可以得到问题的数值解。对于弹塑性材料,其增量形式的本构关系方程为


其中外力向量与式(15)相同,内力向量

由于式(18)中应力是应变的非线性函数,而应变可以由位移插值表示,所以整体上内力向量fin是位移向量u的非线性函数,则方程(17)为以位移为基本未知量的非线性方程,为了对其进行求解,引入Newton⁃Raphson方法进行迭代,迭代格式为

其中弹塑性切线刚度矩阵如式(20)所示
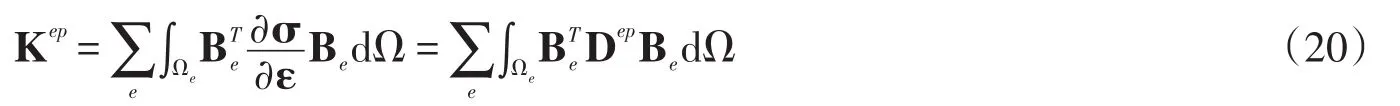
对于材料蠕变问题,材料的弹塑性切线刚度Dep=Dep(t)将与时间显式相关。此时只要在求解过程中考虑应力及刚度与时间的关系,采用与上述相同的迭代格式即可得到问题的数值解。
2.2接触模型
土体变形引起的基桩与上部横梁间相对错动会对结构安全产生很大影响,所以承台与大梁的接触设置需要特别考虑。接触问题是有限元中的一大类问题,其本质是在平衡方程(9)之外引入约束方程,一般采用罚函数法、拉格朗日乘子法或者二者的某种结合。然而,约束方程的引入会改变原始平衡方程的性质,使得最终形成的有限元方程的稳健性减弱,这就是约束条件引入不当经常导致有限元求解失败的原因。所以接触的引入需要十分谨慎,既要具有一定的精度、能够反映工程实际情况,又不能过于复杂以致影响到数值模拟的稳定性和收敛性。
经过研究,选取Abaqus中基于接触面的内聚模型(Surface⁃based cohesive model)作为模拟接触行为的模型,模型的表达式为

式中:t为接触力向量;δ为接触面相对位移;K为接触刚度,Knn为法向刚度,Kss和Ktt为切向刚度。通过定义后3个刚度系数,即可描述接触面的相对运动规律。方程通过罚函数法嵌入到整体结构的分析中。
2.3地应力平衡
在进行包含大体量土体的结构分析时,土体的初始应力场对结果有着很大的影响。因为土体一直是承受着自身重力作用的,所以在自身重力作用所形成的初始应力场作用下,土体的整体竖向位移应该趋近于零。然而在考虑了材料非线性和复杂边坡的情况之后,直接采用预先假定的简单应力分布则不能满足初始位移接近于零,此时则要进行迭代来完成初始应力场的施加。具体步骤如下:
第一,建立模型、材料、分析步;第二,施加自重荷载,完成岩土静力分析步;第三,输出计算结果到odb结果输出文件中;第四,检查土体的位移是否满足要求,如果满足要求,则停止,否则继续进行;第五,将odb文件作为初始应力场,施加到土体上,跳转到第二步。
随着上述过程循环次数的增加,土体的位移可以达到趋于零。
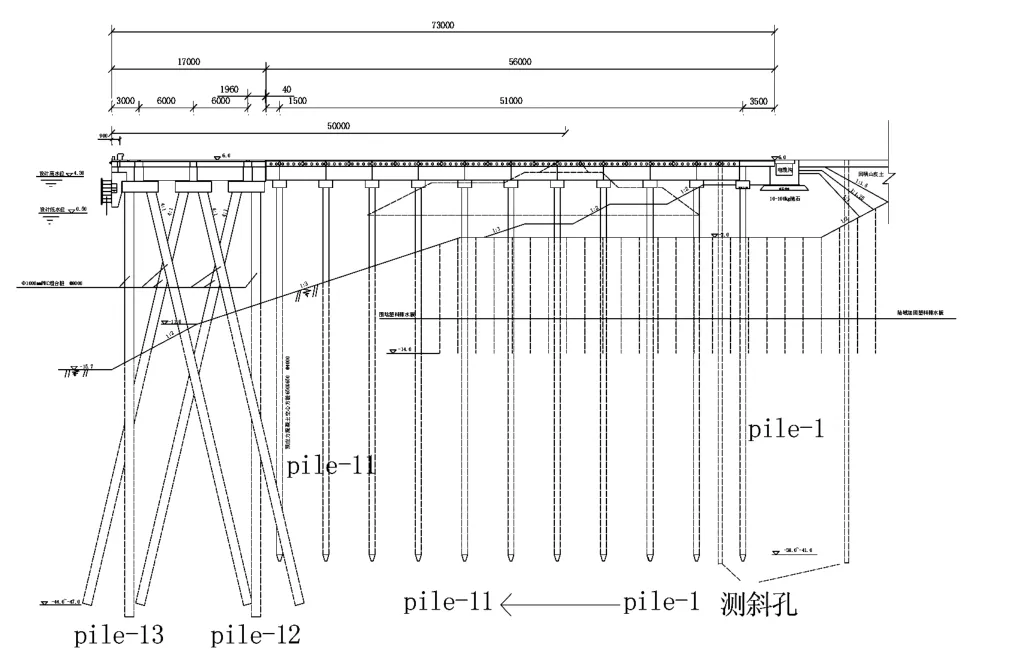
图2 高桩码头结构断面图Fig.2 Sectional view of high pile wharf structure
3计算结果与讨论
天津港是我国的重要港口,近年来随着码头软土地基的蠕变,其高桩码头多处位置出现横梁与基桩之间的错位,并且伴有桩基础的倾斜,严重威胁了码头结构的使用安全。根据近3 a码头的变形观测结果可知,该码头整体的位移趋势是后承台向西南方向位移,累积位移量多在40~70 mm,但码头前承台的位移方向整体偏向西北方向,3 a的累积位移量躲在30~60mm。现场检测发现码头前、后承台伸缩缝已出现混凝土挤压破坏。码头的沉降除了西侧测点在2015年由于管线维修出现了大于10 mm的沉降,其余各测点每年沉降均小于10 mm,累计最大沉降20 mm,主要为挡土墙区域,沉降速度均小0.01~0.04 mm/d,满足相关规范要求。
本文采用结构有限元通用分析程序ABAQUS,建立三维有限元模型对天津港某码头进行计算分析,以期验证上述分析方法的实用性并对该结构加固提供指导。该码头结构剖面如图2所示,将直桩标号为pile⁃1~pile⁃13并根据实际结构建立有限元模型,如图3所示,土体宽度取为24 m,地基土计算深度为-48 m,垂直码头沿线计算方向范围取160 m,码头陆域与后承台交界点为零点,向陆域方向延伸50 m,码头前沿线向海内延伸40 m。荷载考虑为土体与结构自重,同时考虑码头和陆域的均匀堆载60 kPa。

图3 高桩码头结构有限元模型Fig.3 FEM of high pile wharf structure
基桩、桩帽,横梁均为混凝土材料,视为弹性,其弹性模量为30 GPa,泊松比为0.2,密度为2 200 kg/m3。对于桩帽与横梁的接触刚度,垂直接触面方向认为接触刚度很大,取为Knn=3 000 MPa;剪切刚度综合考虑连接等情况,取为Kss=Ktt=20 kPa。
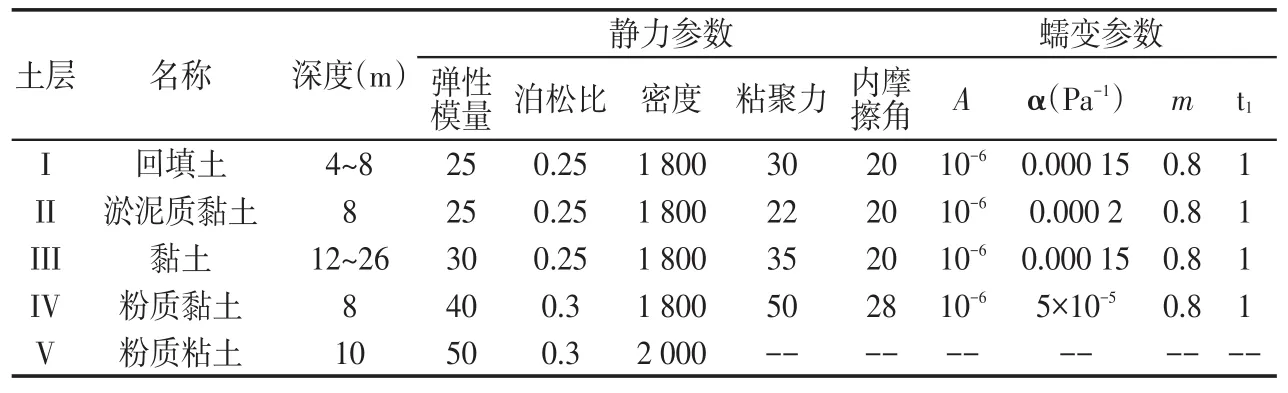
表1 土的材料参数Tab.1 Material parameters of soil
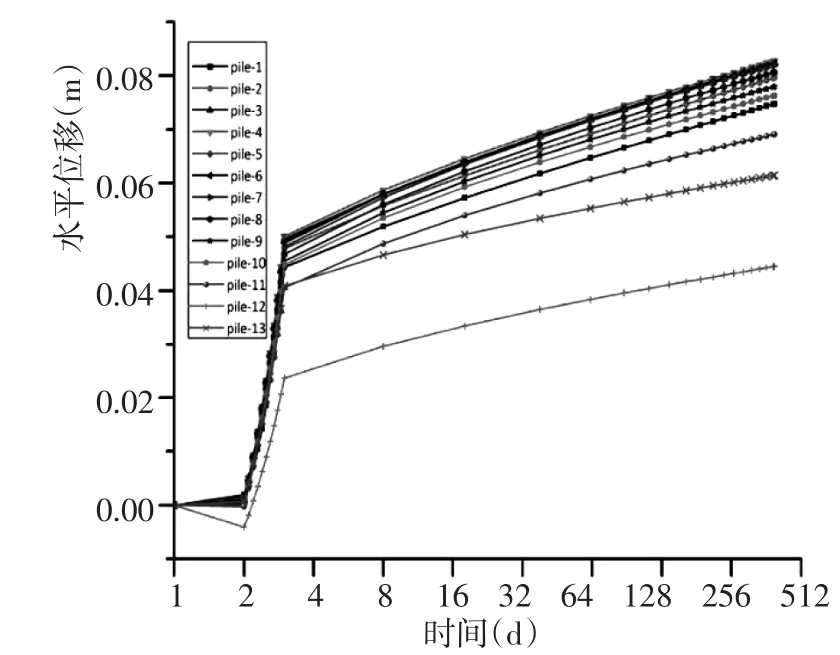
图4 桩顶垂直于岸线方向水平位移随时间变化Fig.4 Horizontal displacement change with time in the direction perpendicular to the shoreline of pile
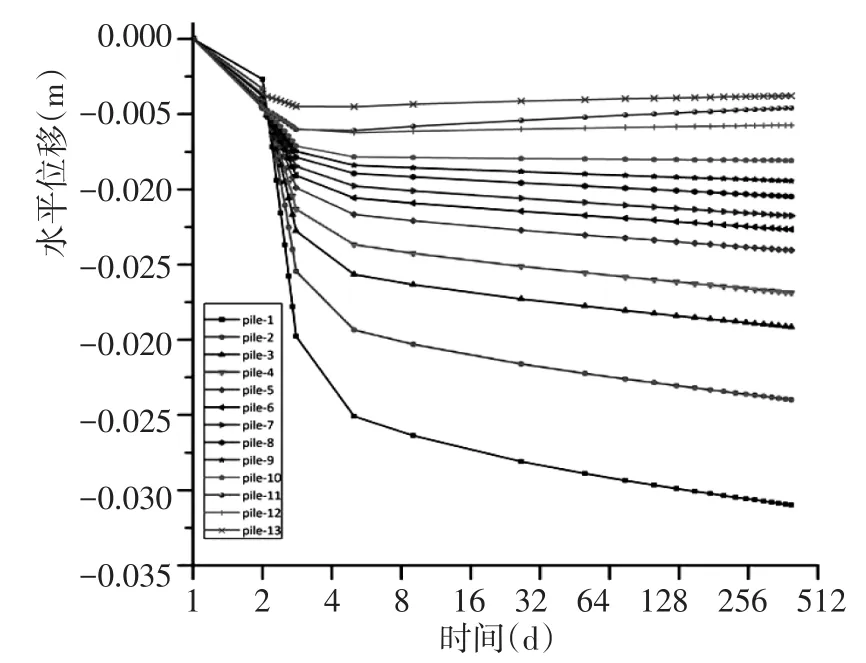
图5 桩顶竖向位移随时间变化Fig.5 Vertical displacement of pile change with time
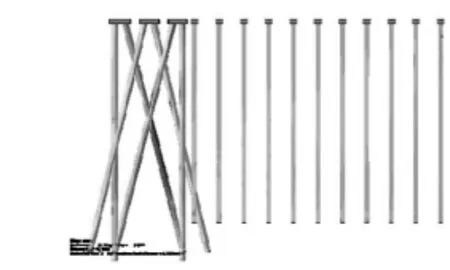
图6 弹塑性变形之后桩身轴向应力云图Fig.6 The cloud of axial stress after plastic deformation of pile

图7 之后桩身轴向应力云图Fig.7 The cloud of axial stress after elastoplastic⁃creep deformation of pile
为了分析和建模的方便,同时又不过多影响模拟的精度,根据地质勘察报告将土层归并为五层。参照试验结果,五层土的材料参数取值如表1。
加载过程中,静力加载共3 d,第一天地应力平衡,第二天结构自重施加,第三天堆载施加,土体同步发生弹塑性变形。第三天之后维持荷载不变,土体发生蠕变变形,直至一年。计算可得一系列结果,桩顶位移如图4、图5所示。
由桩顶位移图可以看出,土体的前期弹塑性变形和后期蠕变变形对桩基顶部位移的影响均较大,且蠕变变形前期较大,后期趋于稳定,相比于接近海域的直桩,接近陆域的直桩受土体蠕变的影响较大。
弹塑性变形后与弹塑性—蠕变变形后的桩身应力云图如图6、图7所示。
由桩身应力云图可以看出,变形后桩身的拉应力水平较高,达到8 MPa,该处易造成PHC桩开裂,桩身的压应力水平在12~15 MPa,在较为合理范围内,不会发生桩身混凝土压碎破坏。
另外,对于排架梁部分,其应力水平总体上不高,但可能会引起局部部位的轻微开裂。接近岸线的两根梁与承台之间发生了明显的错动,蠕变前最大错动4 cm,蠕变后最大错动接近5.5 cm,这个量值的错动在某些情况下可能会影响结构的安全。
分析所得桩顶最大水平位移81 mm与实际观测结果70 mm相近;分析基桩沉降最大值32 mm比实际观测结果20 mm略大;近岸线梁与承台间的错动等现象也发生在实际工程中,可见该数值分析模型与实际结构的变形与损伤具有一定程度的一致性,本文提出的数值分析方法可以较好地反映土体弹塑性变形以及蠕变变形对码头结构的影响。
4结论
本文采用修正的Drucker⁃Prager/Cap模型描述土体的本构关系,并采用Singh⁃Mitchell模型模拟土体蠕变效应,基于三维精细有限元理论,开展了岸坡土体的弹塑性变形与蠕变变形对高桩码头结构影响的数值模型研究,提出了一种模拟长期土体—结构相互作用的分析方法,并将其应用于天津港高桩码头的分析计算。计算结果与实际结构具有一致性,表明本文采用的方法可以较好地反映土体弹塑性变形与蠕变变形对结构的影响。本文也存在一些不足之处和改进方向,由于计算量大,本文未考虑更复杂的工况和混凝土损伤本构模型,未实现码头的损伤现象数值模拟。
[1]邱驹.港工建筑物[M].天津:天津大学出版社,2002.
[2]刘现鹏,韩阳.软基上高桩码头结构节点破坏机理及演化研究[R].天津:交通运输部天津水运工程科学研究所,2015.
[3]闫澍旺,张荣安.天津港南疆突堤蠕变问题的有限元分析[J].港工技术,2003(1):45-47. YAN S W,ZHANG R A.Finite Element Analysis of Creep Deformation of the Breakwater in Nanjiang Area,Tianjin Harbor[J]. Port Engineering Technology,2003(1):45-47.
[4]陈滨.蠕变和差异沉降对桩基影响的数值分析[D].天津:天津大学,2006.
[5]王婷婷.滨海软土流变模型及其在结构物稳定性分析中的应用研究[D].天津:天津大学,2008.
[6]李越松,赵冲久,赵利平,等.天津港岸坡土体蠕变对高桩码头的影响[J].中国港湾建设,2009(4):5-8. LI Y S,ZHAO C J,ZHAO L P,et al.Influence of Bank Soil Creep Deformation on High⁃piled Wharf in Tianjin Port[J].China Har⁃bour Engineering,2009(4):5-8.
[7]丁琼.后方堆载作用下高桩码头变形研究[D].天津:天津大学,2010.
[8]董焱赫.长期循环荷载下饱和软粘土蠕变特性研究[D].天津:天津大学,2013.
[9]Roscoe K H,Schofield A N,Wroth C P.On the Yielding of Soils[J].Geotechnique,1958,8(1):22-53.
[10]Roscoe K H,Burland J B.On the generalized stress⁃strain behavior of wet clay[C]//Engineering Plasticity,HEYMAN J and LECKIE F A(eds).Cambridge,England:Cambridge University Press,1968:535-609.
[11]Hofer D,Kamlah M.Drucker⁃Prager⁃Cap creep modelling of pebble beds in fusion blankets[J].Fusion engineering and design, 2005,73(2):105-117.
[12]李军世,林咏梅.上海淤泥质粉质粘土的Singh⁃Mitchell蠕变模型[J].岩土力学,2000,21(4):363-366.LI J S,LIN Y M.Singh⁃mitchell creep model of Shanghai very soft silt clay[J].Rock and soil mechanics,2000,21(4):363-366.
Research on analysis methods for deformation of high⁃pile wharf under effect of soil creeping
LIU Xian⁃peng,HAN Yang,LIU Hong⁃biao
(TianjinResearchInstituteforWaterTransportEngineering,NationalEngineeringLaboratoryforPortHydraulicConstruction Technology,KeyLaboratoryofHarbor&MarineStructureSafety,MinistryofTransport,Tianjin300456,China)
The elastic⁃plastic deformation and creep deformation of soil will cause large displacement of the high⁃pile wharf structure and influence the structure safety.In this paper,modified Drucker-Prager/Cap model and Singh⁃Mitchell model were used to analyze the high⁃pile wharf under soil deformation.Based on finite element meth⁃od,a method of numerical analysis was proposed to analyze the influence of soil deformation on high⁃pile wharf structure,and it was applied to the analytical calculation of high⁃pile wharf in Tianjin Port.The results show that the method works well on the numerical analysis of Tianjin Port,which offers an alternate way to analyze the wharf under soil deformation.
high⁃pile wharf;soil⁃structure interaction;soil creeping;FEM;bank slope
U 656.1+13
A
1005-8443(2016)04-0432-06
2016-05-13;
2016-07-01
交通运输部建设科技项目(2014-328-224-040,2013-328-224-070);国家自然科学基金(51409134)
刘现鹏(1977-),男,河北省人,高级工程师,主要从事水工构造物检测、诊断与加固技术研究。
Biography:LIU Xian⁃peng(1977-),male,senior engineer.
