半序s－度量空间中积分型压缩映射公共耦合不动点定理

张丹青，柴国庆

（湖北师范大学数学与统计学院，湖北黄石 435002）

半序s－度量空间中积分型压缩映射公共耦合不动点定理

张丹青，柴国庆

（湖北师范大学数学与统计学院，湖北黄石 435002）

给出了s－度量空间中几种形式的公共耦合不动点定理，改进并推广了前人的结果．

s－度量空间；耦合不动点；偏序集；混合单调性；混合g－单调性

0 引言

Banach压缩映象原理［1］被广泛地应用于数学学科及其它领域，成为非线性科学中一个重要工具．近年来，学者们对它进行了各种推广．最近有作者研究了偏序条件下度量空间中的压缩映射不动点定理（见［2－7］），从而开启了广义度量空间中不动点理论的研究．此外，作者们还考虑了各种空间．例如2－度量空间［8］，G－度量空间［8］，D＊－度量空间［10］，锥度量空间［11］，s－度量空间［12］等空间中的不动点定理．

首先介绍一些基本概念和结果，它们在本文中多处用到．

定义1［12］设是X一个非空集合，s∶X3→［0，＋∞）为一个映射．若∀x，y，z，a∈X，满足下列条件：

（P1）∀x，y，z∈X，当x≠y≠z时，则s（x，y，z）＞0；

（P2）s（x，y，z）＝0⇔x＝y＝z；

（P3）s（x，y，z）≤s（x，x，a）＋s（y，y，a）＋s（z，z，a） ∀x，y，z，a∈X，

则s称为s－度量，而称（X，s）为s－度量空间．

引理1［13］在s－度量空间中，有s（x，x，y）＝s（y，y，x）．

定义2［14］设（X，s）是一个s－度量空间，对于∀x∈X，存在x∈X，定义Bs（x，r）是x关于r的开球如下：

定义3［14］设（X，s）是一个s－度量空间，A⊂X．

1）若∀x∈X，∃r＞0，使得Bs（x，y）⊂A，则称A为X中的开集；

2）若∃r＞0，∀x，y∈A，有s（x，x，y）＜r，则称A为s－有界；

3）若s（xn，xn，x）→0（n→∞），则称｛xn｝⊂X收敛于x；

4）若∀ε＞0，∃n0∈ℕ，使得∀n，m＞n0时，s（xn，xn，xm）＜ε，则称｛xn｝⊂X为柯西列；

5）若X中的每个柯西列都收敛，则称（X，s）是完备的；

6）τ是A一个集族，A⊆X，A集合是由所有满足下列条件的x组成：x∈A 当且仅当存在r＞0满足Bs（x，r）⊂A，称τ是X上的拓扑．

引理2［14］设（X，s）是一个s－度量空间．如果当n→∞时，存在序列｛xn｝，｛yn｝满足xn→x，yn→y，则s（xn，xn，yn）→s（x，x，y）．

引理3［15］设（X，s）是一个s－度量空间，则对于任意的x，y，z∈X，有

定义4［16］设（X，≤）是一个半序集．a，b∈X称为可比较的当且仅当a≤b或b≤a成立．

定义5［16］设X是一个非空集合，若下列两个条件成立，则称（X，s，≤）为有序s－度量空间：

1）（X，s）是一个s－度量空间，

2）（X，≤）是一个半序集．

定义6［4］设（X，≤）是一个半序集，H∶X×X→X，称映射H具有混合单调性当且仅当对于任意的a，b∈X，

定义7［17］设（X，≤）是一个半序集，H∶X×X→X，g∶X→X，称映射具有混合g－单调性当且仅当对于任意的a，b∈X，

定义8［14］（a，b）∈X×X称为映射F∶X×X→X和g∶X→X的耦合重合点．如果F（a，b）＝g（a）且F（b，a）＝g（b），如果F（a，b）＝g（a）＝a且F（b，a）＝g（b）＝b时，（a，b）称为耦合不动点．

定义9［18］设X，Y⊂（－∞，＋∞），函数φ∶X→Y称为次可加可积函数当且仅当∀c，d∈X，

定义10［18］（X，s）和（X′，s′）是两个s－度量空间．映射f∶（X，s）→（X′，s′）是一个函数，称f在a∈X连续当且仅当对于任意X中的序列xn，s（xn，xn，a）→0可得到s′（f（xn），f（xn），f（a））→0．f 在X上连续当且仅当对于任意的a∈X都连续．

引理4［18］设｛rn｝n∈ℕ是一个非负序列，满足n→∞时rn→a．则

其中φ∶［0，＋∞）→［0，＋∞）是在［0，＋∞）上的任何有界闭集，且对于任意ε＞

引理5［18］设｛rn｝n∈ℕ是一个非负序列当且仅当limrn＝0，其中φ∶［0，＋∞）n→∞→［0，＋∞）是在［0，＋∞）上的任何有界闭集，且对于任意ε

1 主要结果

定理1 （X，s，≤）是一个半序s－度量空间，H∶X×X→X和g∶X→X是两个映射．其中H满足混合g－单调性．如果存在a0，b0∈X，满足g（a0）≤H（a0，b0），g（b0）≥H（b0，a0），且存在正实数k1和k2满足k1＋k2∈（0，1），满足下列条件

其中a，b，c，p，q，r∈X，ga≥gp≥gc且gb≤gq≤gr或ga≤gp≤gc且gb≥gq≥gr．

φ∶［0，＋∞）→［0，＋∞）是一个非负Lebesgue可积的映射，且满足可列可加性，且对于∀ε＞0，有，满足下列条件：

1）H（X×X）⊂g（X），

2）g（X）是完备的，

3）g是连续的且关于H可交换．

那么H和g存在一个耦合重合点．进一步地，如果gp＝gc且gq＝gr，那么存在a∈X，满足g（a）＝H（a，a）＝a．

证明：设a0，b0满足g（a0）≤H（a0，b0），g（b0）≥H（b0，a0），由于H（X×X）⊂g（X），故存在a1，b1∈g使得g（a1）＝H（a0，b0），g（b1）＝H（b0，a0）．又由于H（X×X）⊂g（X），同样存在a2，b2∈g使得g（a2）＝H（a1，b1），g（b2）＝H（b1，a1）．重复以上过程，可得到X中的两个序列｛an｝，｛bn｝满足

其中n∈ℕ．

下面证明∀n∈ℕ，有

应用归纳法，当n＝0时，由于

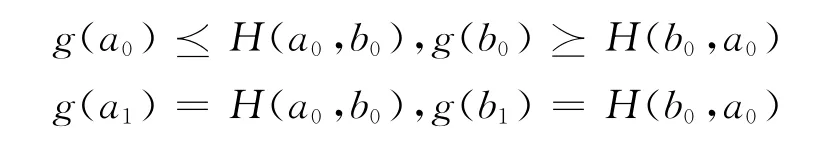
故g（a0）≤g（a1）．现假设存在一个n≥1，使得（3），（4）成立，则由（2）式可得

故∀n∈ℕ，（3）－（4）成立．于是由于g（an＋1）＝H（an，bn），g（bn＋1）＝H（bn，an），故当（an，bn）＝（an＋1，bn＋1），有g（an＋1）＝g（an）＝H（an，bn），g（bn＋1）＝g（bn）＝H（bn，an）

我们断言：H和g存在一个耦合重合点．事实上，假若

即

由于g（an）≤g（an＋1），g（bn）≥g（bn＋1），故由（1）得

当m＝2p时，有

由于k1＋k2＜1，故当n，m→∞时，s（gam，gam，gan）→0．所以｛gan｝是g（X）中的柯西列．类似地，可以证明｛gbn｝是g（X）中的柯西列．因为g（X）是完备的，所以X中存在a，b使得当n→∞时，gan→a，gbn→b．由于g是连续的，故

由于g和H是可交换的，故有

现证，（a，b）是H和g的耦合重合点．事实上由（1），有

由于g是连续的，故当n→∞，有

所以ga＝H（a，b）．类似地，我们可以证明gb＝H（b，a）．

接下来我们证明H（a，a）＝g（a）＝a．由于（a，b）是H和g的耦合重合点，故有g（a）＝H（a，b），g（b）＝H（b，a）．

假设ga≠gb，由（1），我们有

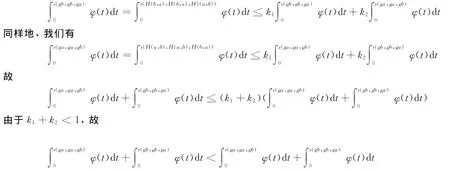
矛盾．故ga＝gb，于是H（a，b）＝ga＝gb＝H（b，a）．

又由于n→∞时，gan＋1＝a，gbn＋1＝b，故

由于g是连续的，当n→∞，有

类似地，我们可以得到

由于k1＋k2＜1，故上式成立当且仅当s（ga，ga，a）＝s（gb，gb，b）＝0．故ga＝a，gb＝b．由此得到ga＝H（a，a）＝a．

应用举例

其中k1

故定理1条件成立．故存在a∈X，ga＝H（a，a）＝a，其中a＝0．

［1］Banach S．Sur les operations dans les enseembles abstraits et leur application our equations intergrals［J］．Fundam Math，1922，3：133～181．

［2］Agarwal R P，EI－Gebeliy M A，Oregan D．Generalized contractions in partially ordered metric spaces［J］．Appl Anal，2008，78（1）：109～116．

［3］Altun I，Simek H．Some fixed point theorems on Ordered metric spaces and application［J］．Fixed Point Theory App，2010，（1）：1～17．

［4］Bhaskar T G，Lakshmikantham V．Fixed point theorems in partially ordered metric spaces and applications［J］．Nonlinear Analysis，2006，65，1379～1393．

［5］Ciric Lj，Mihet D，Saadati R．Monotone generalized contractions in partiality ordered probabilitic metric space［J］．Topology and its Appl，2009，156（17）：2838～2844．

［6］Hadzic O．On common fixed point theorems for weakly contractive mappings in partially ordered sets［J］．Nonlinear Anal，1982，71：7～8．

［7］Harjani J，Sadarani K．Fixed point theorems for weakly contractive mappings in partially ordered sets［J］．Nonlinear Anal，2008，71：3403～3410．

［8］Gahler S．2－metrische Raume und ther topoloische Struktur，Math［J］．Nachr，1963，26：15～148．

［9］Mustafa Z，Sims B．A new approach to generalized metric space［J］．J Nonlinear Convex Anal，2006，7：289～297．

［10］Sedghi S，Shobe N，Zhou H．A common fixed point theorem in L－metric spaces［J］．Chaos Soliton S ＆Fractals，2007，33（2）：358～363．

［11］HUANG L G，ZHNG X．Cone metric spaces and fixed point theorems of contractive mappings ［J］．J Math Anal App，2007，332：1468～1476．

［12］Sedghi S，Shobe N Aliouche．A generalization of fixed point theorem in S－metric spaces［J］．Mat Vesnik，2012，64：258～266．

［13］Sedghi S，Altum I，Salahshour N．Some properties of S－metric space and fixed point results ［J］．Kyungpook Math J，2014，54：113～122．

［14］Sedghi S，Shobe N，Dosenovic T．Fixed point results in S－metric spaces［J］．Nonlinear Functional Analysis and Applications，2015，20（1）：55～67．

［15］Dung N V．On coupled common fixed points for mixed weakly monotone maps in partially ordered S－metric spaces［J］．Fixed Point Theory Appl，2013，2013（1）：1～11．

［16］Hemant K．Coupled common fixed point results ordered G－metric space［J］．Journal of Inequalities and Applications，2012，2012（1）：1～13．

［17］Ciric L j，Lakshmikantham V．Coupled random fixed point theorems for nonlinear contracitons in partially ordered metric spaces［J］．Stoch，Anal，Appl，2009，27（6）：1246～1259．

Common couple fixed point theorems for integral type mappings in ordered s－metric spaces

ZHANG Dan－qing，CHAI Guo－qing

（College of Mathematics and Statistics，Hubei Normal University，Huangshi 435002，China）

Several common couple fixed point results for integral type mappings in ordered s－metric spaces are given，which improve and generalize the previous results in the literature．

s－metric space；coupled point；partially ordered set；mixed monotonity；mixed g－monotonity

G250

：A

1009－2714（2016）04－0051－07

10．3969／j．issn．1009－2714．2016．04．012

2016—05—10

张丹青（1989— ），男，贵州六盘水人，硕士研究生，研究方向为非线性泛函分析．