基于整体分布优化算法的闭塞分区划分优化
2016-02-16王丹彤倪少权张文泉
王丹彤,倪少权,张文泉
(1.西南交通大学 信息科学与技术学院, 成都 611756;2.西南交通大学 交通运输与物流学院,成都 611756)
基于整体分布优化算法的闭塞分区划分优化
王丹彤1,倪少权2,张文泉1
(1.西南交通大学 信息科学与技术学院, 成都 611756;2.西南交通大学 交通运输与物流学院,成都 611756)
本文将整体分布优化算法应用于闭塞分区的划分,设计了适应于闭塞分区划分的优化算法。通过MATLAB编程进行仿真,对整体分布优化算法和粒子群算法进行比较,并对优化结果进行检验,结果表明,整体分布优化算法的优化效果比粒子群算法更优,且优化结果满足实际需求。
闭塞分区;追踪间隔;整体分布优化算法
为保证列车安全和铁路线路必要的通过能力,把铁路线路分成若干个长度不等的段落,每一段线路叫做一个闭塞分区。闭塞分区划分时,要求列车运行兼顾安全、经济与效率,对于改善铁路运营能力具有重要的意义[1]。本文采用整体分布优化算法,能够快速合理地完成闭塞分区的划分。
1 闭塞分区划分优化模型
1.1 模型定义[2~3]
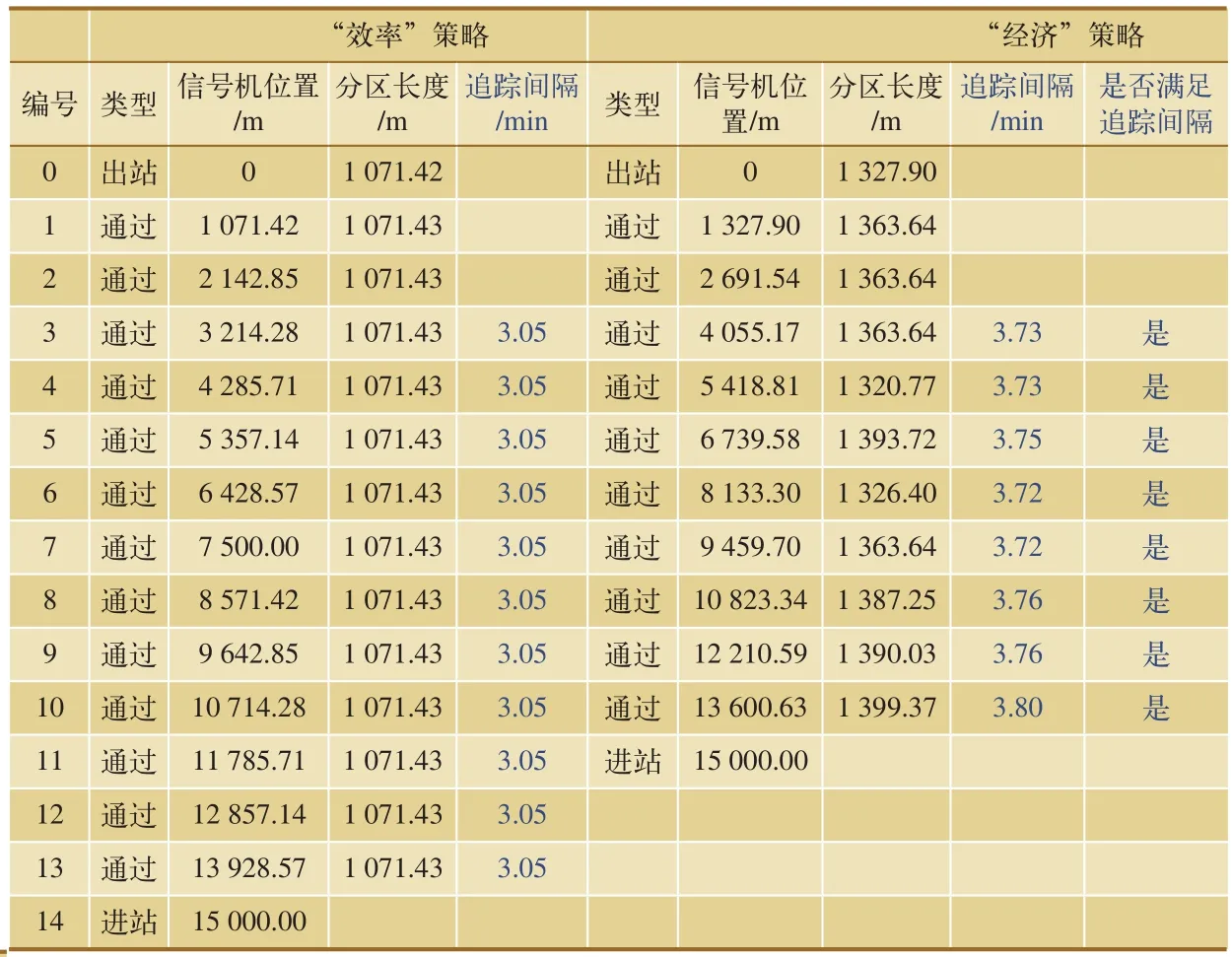
如图1所示,设两站间信号机一共N架,每架信号机的位置坐标为xi(i=1,2,…,N),x0、xN+1分别为两车站间的出站信号机和进站信号机的位置坐标,则闭塞分区长度为li=|xi-xi-1|,(xi-1 图1 闭塞分区模型 1.2 优化目标 闭塞分区的划分是在保证行车安全及具体施工要求的约束条件下,找出划分节点,求得最短追踪间隔。根据划分闭塞分区的侧重点不同,一般有两种划分策略:“效率”策略和“经济”策略。 “效率”策略是指列车制动距离和闭塞分区有效长度满足的情况下,通过最小化追踪间隔时间得到最大的列车通过能力,从而提高自动闭塞分区上的列车运行数目。其目标函数为: “经济”策略是指在列车追踪间隔时间确定的前提下,最小化信号的数目。其目标函数为: 其中,N表示两站间信号机的架数。 1.3 约束条件 闭塞分区实际划分时要考虑多个约束条件,包括列车紧急制动距离、轨道电路长度、区间最小分区数目等。 其中,lmin为工程人员由现场实际情况确定的闭塞分区最短长度,lcircuit为轨道电路极限长度,划分闭塞分区个数n=N+1,H为预先设定的追踪间隔时间。制动距离Sb和附加距离S附长度之和为闭塞分区长度li, maxSb(vi,vi+1,ij)为列车自坡道值ij处从高速度等级vi+1降至相邻低速度等级vi的最大制动距离[3~5]。 1.4 适应度函数 由上可知,闭塞分区的划分有诸多约束条件。将诸多条件以惩罚函数的形式引入,从而构造出无约束的适应度函数。 “效率”策略下的适应度函数为: 其中,C 为常系数,调节适应度的值在一定范围;a 为惩罚因子,取值为100~1 000。 在“经济”策略下,适应度函数为: 其中,λ为惩罚因子,取值为10~20。 2.1 整体分布优化算法简介 粒子群(PSO)算法作为一种有效的优化算法,已经在闭塞分区的划分中得到了应用[2,5]。整体分布优化算法是一种衍生于PSO算法的新优化算法。与PSO算法比较,具有实现简单、收敛速度快、鲁棒性强等特点。具体的计算过程如图2所示[6]。 图2 整体分布优化算法程序流程图 2.2 闭塞分区划分过程 根据整体分布优化算法的计算流程来设计闭塞分区的划分过程,具体过程如下: (1)根据式(3)的约束条件,随机生成闭塞分区个数n。 (2)将区间n等分,得到一组可行解X(i),i=1,2,…,n-1。则线路上第i架信号机位置取值范围为:X(i)-300≤x(i)≤X(i)+300。 (3)随机初始化种群,种群维度为n。找出最优解记为Gbest。 (4)进行迭代,找出本次迭代后种群的最优解Lbest。 (5)Lbest比Gbest更优,则转至(6),否则停滞次数β减1,若β≠0,则转至(6),否则种群直径D←D · α,β←9。 (6)以已经找到的最好个体的坐标作为中心,用柯西分布产生新的种群。且最大迭代次数减1。 (7)判断是否满足迭代终止条件。若最大迭代次数imax=0或D 假设甲乙两站区间待布置,甲站出站信号点坐标为0 km,乙站进站信号点位置坐标为15 km。列车在区间的平均运行速度为100 km/h,列车长度为0.8 km,利用MATLAB编程进行仿真分析。 整体分布优化算法和PSO算法都能够很快收敛,为了更为直观的比较整体分布优化算法和PSO算法,种群数取20,迭代次数取250。在“效率”策略下,分别进行50次仿真,比较两种算法的最优最适应度和平均适应度,平均适应度如图3所示,最优适应度见表1。 图3 平均适应度比较(“效率”策略) 在“经济”策略下,设定最大追踪间隔H=4 min。进行50次仿真,比较两种算法的最优适应度和平均适应度,平均适应度如图4所示,最优适应度见表1。 表1 最优适应度比较 图4 平均适应度比较(“经济”策略) 由图3和图4可知,在“效率”策略和“经济”策略下,整体分布优化算法比PSO算法的平均适应度都要更优。显然,整体分布优化算法较之PSO算法,能找到更优的解,且具有更好的鲁棒性。 由表1可知,在“效率”和“经济”策略下,整体分布优化算法的最优适应度值均小于PSO算法的最优适应度值。 综上所述,整体分布优化算法比PSO算法更优。因此,当整体分布优化算法最优适应度收敛到最小值时,取此时的解作为该策略下的布置方案最为合理,布置结果如表2所示。 表2 整体分布优化算法的布置方案 从表2可以看出,在“效率”策略下,甲乙两站之间架设13架通过信号机,此时的最大追踪间隔时间为 max(I1,I2,…,Ik) =3.05 min;在“经济”策略下,两站之间共架设通过信号机10架,最大追踪间隔 max(I1,I2,…,Ik)=3.80 min 本文将整体分布优化算法应用于闭塞分区的划分,分别在“效率”策略和“经济”策略下比较了整体分布优化算法和PSO算法的适应度值。整体分布优化算法搜索最优解的能力更强,鲁棒性也更优。最后通过实例进行仿真分析,并根据整体分布优化算法的输出结果形成布置方案。 [1]王瑞峰.铁路信号运营基础[M].北京:中国铁道出版社,2008. [2]康 宁,陈永刚,林俊婷,曹 岩.基于免疫粒子群算法的闭塞分区划分优化设计[J].铁道标准设计,2013(11). [3]刘剑锋,毛保华,侯忠生,等.基于遗传算法的区间自动闭塞信号机布置优化方法[J].铁道学报,2006(8). [4]左政伟,王思明.面向闭塞分区划分问题的模拟退火算法研究[J].科学技术与工程,2012(12). [5]林 祁.基于粒子群算法的铁路闭塞分区设计优化研究[D].成都:西南交通大学,2009. [6]余炳辉.整体分布优化算法研究及应用[M].成都:西南交通大学出版社,2012. 责任编辑 陈 蓉 Optimization of railway block range partition based on entire distribution optimization algorithm WANG Dantong1,NI Shaoquan2,ZHANG Wenquan1 In this paper,the entire distribution optimization algorithm was applied to the block range partition,and the optimization algorithm was designed to adapt to the partition.Through MATLAB programming simulation,the entire distribution optimization algorithm and particle swarm optimization algorithm were compared,and the optimization results were tested.The results showed that the optimization effect of the entire distribution optimization algorithm was better than the particle swarm optimization algorithm,and the optimization results could meet the actual needs. block partition;tracking interval;entire distribution optimization algorithm U284.4∶TP39 A 1005-8451(2016)06-0048-04 2015-12-08 中国铁路总公司科技研究计划项目(2014X004-D)。 王丹彤,在读硕士研究生;倪少权,教授。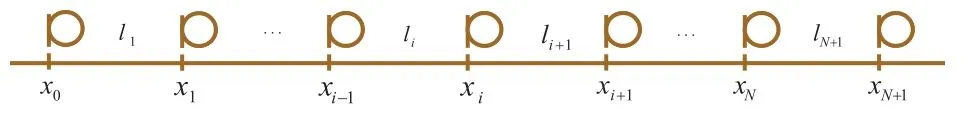
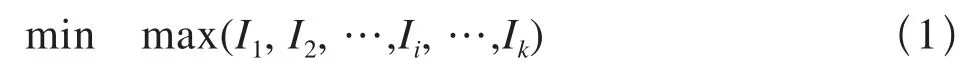


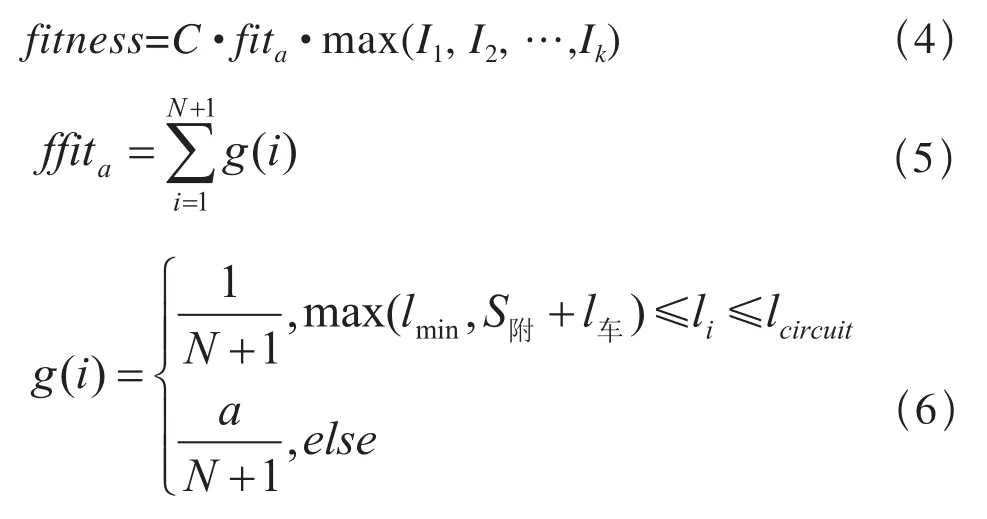
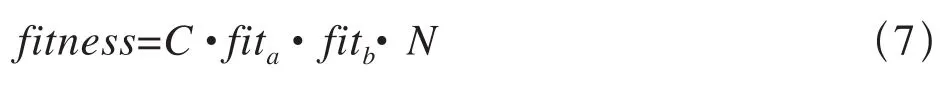
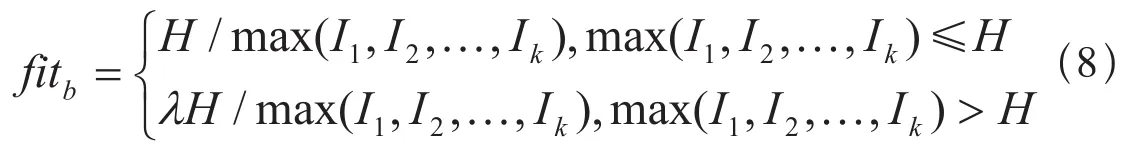
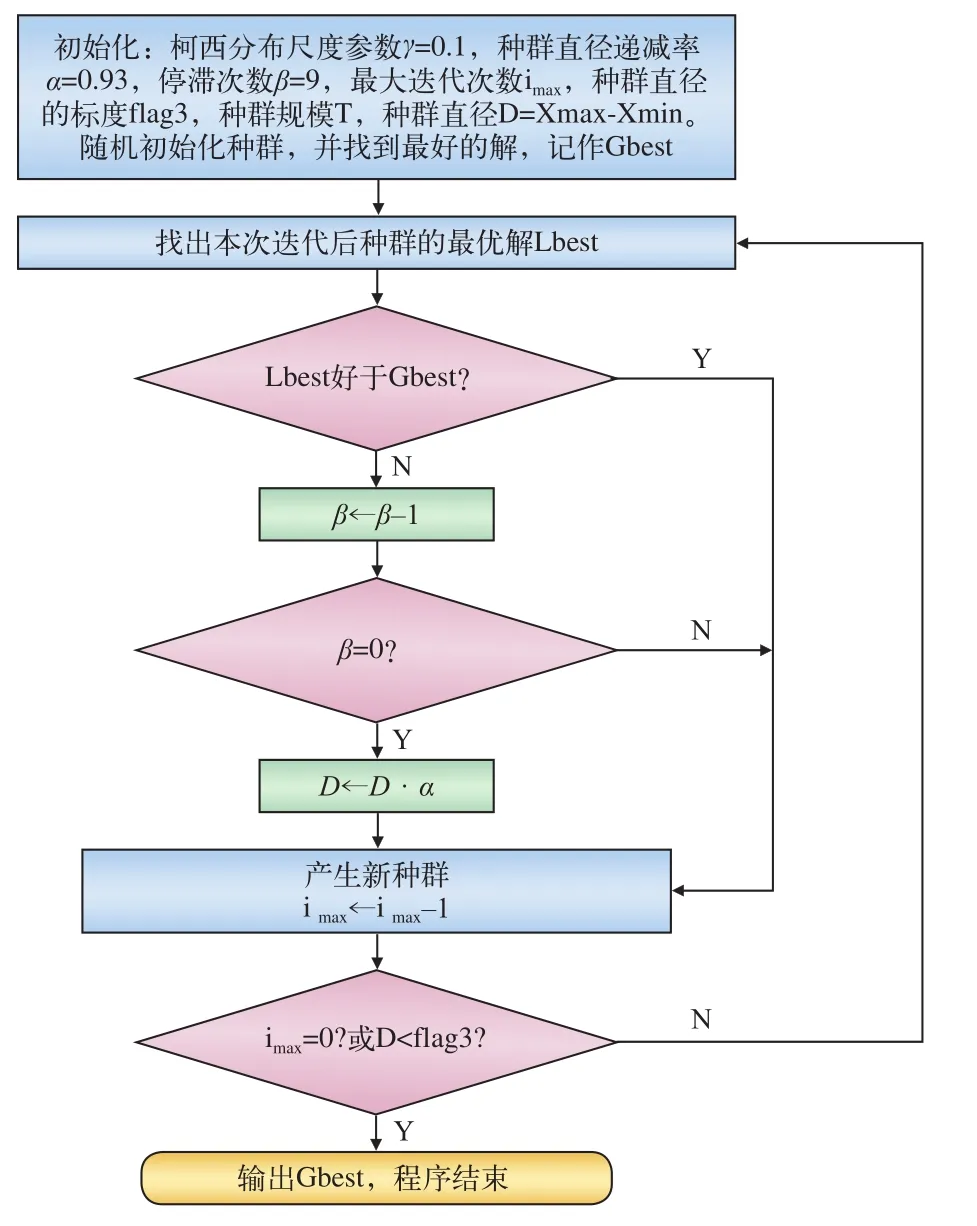
2 整体分布优化算法的优化过程
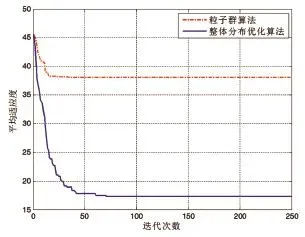
3 仿真分析

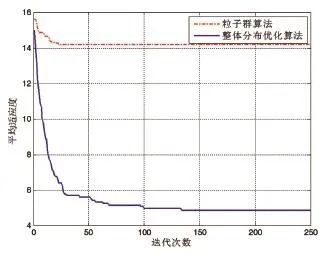
4 结束语
( 1.School of Information Sciences and Technology,Southwest Jiaotong University,Chengdu 611756,China;2.School of Transportation and Logistics,Southwest Jiaotong University,Chengdu 611756,China)
