多药合用药效学协同、相加和拮抗定量计算新方法的建立

袁守军

（军事医学科学院放射与辐射医学研究所药物毒理与肿瘤药理实验室，北京 100850）

多药合用药效学协同、相加和拮抗定量计算新方法的建立

袁守军

（军事医学科学院放射与辐射医学研究所药物毒理与肿瘤药理实验室，北京 100850）

袁守军，博士，研究员，博士生导师，军事医学科学院放射与辐射医学研究所药物毒理与肿瘤药理课题组长。研究方向为肿瘤药理、定量药理、药物相互作用、新药评价、毒代动力学和抗辐射药物等。发表学术论文75篇，其中SCI论文15篇，出版专著《多药合用药效相加的数学规律及协同拮抗的定量计算方法》。完成自然科学基金项目6项、国家重大项目肿瘤药效学平台项目2项及抗癌药物等临床前评价项目愈百项。担任国家和军队新药审评专家、中国定量药理学会常委、军队肿瘤药理专业委员会委员和中国应用药理学会委员等。

许多严重疾病如癌症的病因复杂，属于多靶点疾病，针对多个靶点联合用药比单靶点用药更容易实现治疗目的。药物联用可产生多层面的相互作用，最终表现为药效发生协同、相加或拮抗。对其进行定量评价的前提是获得多药合用组合的预期相加效应值。但长期以来一直缺乏精确计算协同、相加和拮抗的可靠方法，使新复方药物研究等发展受阻。通过等效剂量兑换和引入药理学中的药效的序贯和集合原理，作者发现了多药合用组合预期相加效应的数学规律，简述如下：多药合用剂量组合的预期相加效应值是一个连续的数值范围，即预期相加效应值是药物组合剂量的闭区间数集函数，建立了通用型计算公式。在二维坐标系中显示为一条量效曲带，与多药合用组合的实际量效曲线构成一幅“一条曲带和一条曲线”的图像。组成预期相加量效曲带的量效曲线的数量，随着合用药物数量的增加呈指数性增长。通过计算实际量效曲线和相加量效曲带的交点坐标，能够得出多药合用组合药效发生协同、相加或拮抗的剂量范围；通过比较实际量效曲线中的效应值（或剂量值）与相加量效曲带的偏离状况，能够得出发生协同、相加或拮抗程度的指标，如剂量合用指数和效应合用指数等。该方法能为新复方药物研发、多药联合效应的定量评价和中药复方的效应评价等提供可靠通用的计算方法，简称为“一带一线”法。

多药合用；药物相互作用；定量评价；预期相加效应；量效曲带；协同；相加；拮抗；一带一线法

许多严重疾病的病因复杂，涉及多靶点、多环节，需针对多个环节方能奏效。而研发针对多靶点、多环节的单一结构的化合物新药，几乎是很难完成的任务。从解决问题的可行性和实际效果来看，联合用药或者研发新复方药物，能为疾病治疗和新药研发开辟更宽的路径。

在现代医疗实践中，很少使用单一药物，常需要多药联用，少则2～3种，多则7～8种，甚至10多种。药物联用是对疾病最有效的治疗手段之一。中国传统医学中，多种动植物或矿物药物的联合使用或者组成的固定复方更是常见。

多药联合应用的动因，包括对疾病的治疗，需要针对多个环节或者多个靶点；患者常有多种疾病；疾病除了对因治疗外，尚需对症治疗；药物的适应症和治疗窗口是有限的，且有不同性质和不同程度的副作用。因此，联合用药的目的，是获得最大的治疗效果，最大程度地减轻毒副作用。对于一些严重疾病的治疗，如恶性肿瘤、感染性疾病和心脑血管疾病等，药物联用的治疗效果是非常显著的。

在新药研发中，对各类型新复方药物的研发，实际上是将发挥最优治疗用途的多种药物联合应用，进行最大合理性的固定化。另外，新药研究均包含药物相互作用的内容，并要求在其说明书中标明。对于单一结构新药的研发，药政部门愈发关注与其它药物合用是否增效及安全。

1 药物相互作用的层面

理化性质的相互影响是指药物在配伍和合用时，理化性质方面发生的改变。药政部门对于临床所用药物的配伍禁忌有严格的使用规定，药物配伍禁忌表会不断更新。

机体代谢能力的相互影响是指一种药物暴露于机体负责药物代谢的组织和器官时，可对另外一种药物的体内暴露产生重要影响，进而会引起药效以及毒性的改变。药政部门颁布的药物相互作用影响的指导原则，针对的就是该部分。

药物效应之间的相互影响是指作用机制不同或者相似的药物合用时，药物效应的增强或者减弱。

给药顺序（序贯）的影响是指多药合用时，由于药物起效顺序的不同，所致组织细胞状态发生改变，因而导致药物效应发生改变。其药理学基础为当机体组织细胞的功能状态发生改变时，对药物的反应性也会发生改变。

药政部门对前两者有明确的管理指导规范，对后两者则缺乏具体的指导方法。不论药物相互作用发生于何种层面，均会使药物的效应发生改变，或协同、或相加、或拮抗。在临床实践中，当医生开出多个药物联合应用的处方后，会因药物间的相互作用使患者面临极大的疗效和毒性风险。在新药研发中，多成分复方新药的研发常常受阻，原因在于新药研发者必须证明药物联合使用比单一使用效果好，也就是定量地评价协同、相加和拮抗。因此，定量评价多药合用所致的药效改变，一直是药理毒理学、临床药学和新药研发中的薄弱环节，为医药工作者所关注。

2 协同、相加及拮抗定义的共识和不足

药物联用所致的药效协同、相加和拮抗，其定义多年来一直没有统一。Chou［1］曾撰文，列举了从1874-1995年有关协同和拮抗定义的相关重要论述31篇。直到20世纪90年代才形成共识。协同是实际药效大于预期相加作用，相加是实际药效等于预期相加作用，拮抗是实际药效小于预期相加作用。而不是简单的描述为药物效应增强或者减弱。从药物效应层面上看，协同和拮抗，实际上是药物之间发生了相互作用；相加，则没有发生相互作用，因此，药物相加的定义又扩展为零相互作用［2］。另有一种通俗形象的说法，相加为“1+1=2”，而协同为“1+1>2”，拮抗为“1+1<2”［3］。从剂量角度来看，在某一药效水平下，协同是合用剂量小于预期合用剂量，相加则是合用剂量等于预期合用剂量，拮抗是合用剂量大于预期合用剂量。

多药合用时，药效发生协同还是拮抗，确定预期相加作用是非常关键的，是发现药物联用最优化方案的基础。从数学函数或者量效关系层面去定义预期相加效应，是建立定量计算协同、相加和拮抗的前提。但目前均没有从数学函数或者量效关系的层面，对药物合用的预期相加进行定义。

3 协同、相加及拮抗计算方法的现状

联合用药效应评价的定量计算方法，自1871年Fraser［4］首次用图解法表征2个药物的相互作用起，100多年来有许多学者描述了多种的计算方法，仅Greco等［5］在1篇综述中归纳总结的协同和拮抗的计算方法就有13种之多。近20年来，有关新方法的进展较少。公认的方法仍然是Loewe的等效线相加模型和Bliss的独立模型［5-6］，其他方法多是基于这2种方法的推导和演化，如等效线图法、Bürgi公式法、分数分析法、中位效应法、效应表面模型、金氏公式法和分数乘积法等。综合这些方法和评价指标，也同样没有从数学函数或者量效关系的层面，对药物合用的预期相加进行明确定义或充分证明，属于经验公式或共识性公式，或者仅适用于特定情况，应用范围有限［7-12］，很难经得起数学和药理学的双重推导及检验，全面精确计算多药合用药效变化的相关数据则较为困难。

目前，多药合用的定量评价常常是将药物合用组与药物单用组进行简单比较。如为两药按固定比例的联合应用，用Loewe等［7］效线相加模型或相关模型进行计算；如为质反应数据，则选用Bliss独立模型等方法计算。对于其他类型药物联合方式，较多药物的联合应用，以及新药多成分、复杂复方制剂的研发，则缺乏可靠的药效（毒效）定量计算方法。总体情况较为混乱，同一组数据用不同的计算方法常常会得出不同的结论。以至于有学者认为，“没有具体方法和标准”才是评价计算药物协同、相加和拮抗的方法［2，13-14］。

因此，当多个药物联合应用时，如何确定其药物效应发生协同、相加或拮抗，并对其进行定量计算的、科学严谨的通用方法，长期以来一直没有得到解决，已经成为长期困扰药物学研究领域中的难题，有必要发展一种科学的、严谨的、通用的定量计算方法。

4 多药合用药效预期相加的数学规律

4.1 通用数学方法建立的策略和药物联用时量效关系的数据特点

由于药物种类多样，作用机理各异，因而通用模型的建立，不能将作用机理作为依据，必须以共同的药效为目标，才能使算法具有通用性。另外需将多药合用药效复杂相互作用关系的数据进行归纳和抽象化，使之能够用于逻辑推理和数学运算，使数学原理和药理学规律充分融合。基于此原则，通过观察多药合用时各个药物成员单用和合用量效关系的状况，能够发现一些共同的特点。

特点1：多药联合应用时，不论药物单用组，还是各种药物合用组，均是以药物效应为共同目标中心，作为共同的观察终点。药物目标效应与各自药物组的剂量，能分别构成量效函数关系。各组数据既单独成立又相互影响，类似“大蒜样”的构型。“蒜柱”可看作是药效，各单药和联合用药组构成的量效关系，可看作是“蒜瓣”，围绕着药效（蒜柱），各组之间彼此独立又紧密联系。这样可以药效（蒜柱）为中心，依次展开同等条件下的等效剂量兑换（简称“等效剂量兑换”）。

特点2：药效的物质基础是药物分子与生物大分子的相互作用，如：受体、离子通道、酶、核酸等。药物的量效特征，也体现为药物分子与生物大分子相互作用的特征。药物分子只有结合达到一定的量才可产生药物活性；如果药物分子与生物大分子的结合达到饱和，药效也趋于饱和。因此，药物量效曲线的函数特征是有界函数，即药效强度值是有界的，药物剂量则包括最小起效剂量和最大饱和效应剂量。如果选择的药物剂量窗口足够宽，相邻剂量间距较小，大多数药物的量效关系曲线应为“S”形。

特点3：药物效应具有序贯特征，基础是药效受组织细胞状态的影响。多种药物合用时，会因给药和药效发生顺序（序贯）的不同，造成的药效强度有明显不同，药效序贯特征是药理学的铁律之一。

特点4：药物效应具有集合特征。药效的执行者如：细胞、酶分子、受体、离子通道、血管平滑肌、肌束等均可抽象地概括为药效执行单位。机体有成千上万亿个药效执行单位，全体药效执行单位的活性总和汇集为整体药效。药效集合特征也是药理学的一条铁律。

4.2 多药合用药效预期相加数学规律的描述

题目：药物A和药物B，有共同的目标药效Y，各自的量效关系分别为Y=f（x）和Y=g（x）。药物A的剂量为Am时，药效值为Y=f（Am）；药物B的剂量为Bn时，药效值为Y=g（Bn）。当Am和Bn合用时，预期相加药效值Yexp=？，并非f（Am）+g（Bn）。解答如下：

规律1：两药合用相加效应值可分解为，在一个药物药效水平的基础上，另一个药物遵循自己的量效曲线前行到自身剂量达到的效应值，反过来也成立，即序贯相加规律（图1）。

图1 序贯相加规律示意图.

图1的上图是在药物B的药效g（Bn）水平基础上，药物A沿着自己的量效曲线，前进Am剂量达到的药效值，即Yexp=Y（Am+Bn）；下图是在药物A的药效f（Am）水平基础上，药物B沿着自己的量效曲线，前进Bn剂量达到的药效值，即Yexp=Y（Bn+Am）。由于药物A和药物B作用方式不同，预期相加效应Yexp则存在Y（Am+Bn）≠Y（Bn+Am），预期相加效应序贯相加的公式组（1），如下：

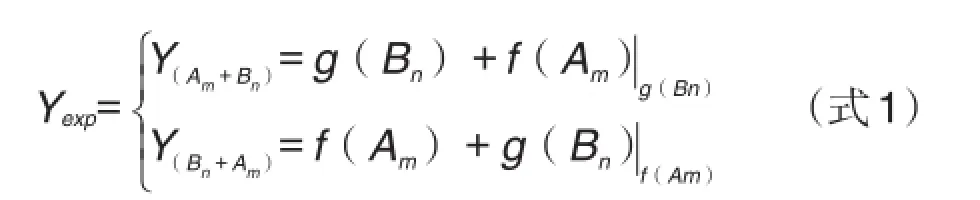
Yexp：预期相加效应（expected additive effect）；g（Bn）：药物B在剂量Bn下的药效；f（Am）|g（Bn）：在药物B的药效g（Bn）水平基础上，药物A沿着自己的量效曲线，前进Am剂量达到的药效增量；f（Am）：药物A在Am下的药效；g（Bn）|f（Am）：在药物A的药效f（Am）水平基础上，药物B沿着自己的量效曲线，前进Bn剂量达到的药效增量。

规律2：将一个药物作为目标药物，另一个药物剂量与目标药物进行等效剂量兑换后，预期相加量效曲线的函数关系与目标药物的函数关系相同，预期相加效应值为等效剂量与目标药物剂量合并的函数值（图2），即计算方法。

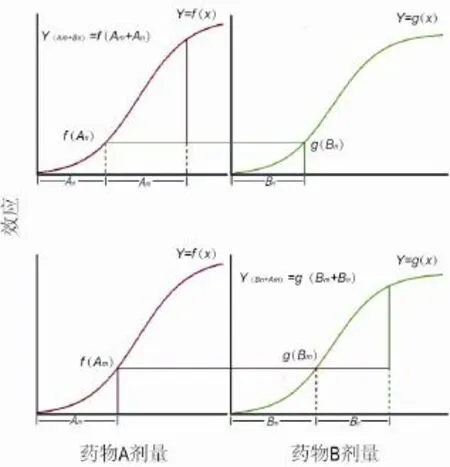
图2 药效序贯相加的计算规律示意图.

图2的上图是以药物A作为目标药物（参比药物），药物Bn等效兑换为An，即g（Bn）=f（An），Yexp=Y（Am+Bn）=f（Am+An），与药物A的函数关系相同，均为“f”。下图是以药物B作为目标药物（参比药物），药物Am等效兑换为Bm，即f（Am）=g（Bm），Yexp=Y（Bn+Am）=g（Bm+Bn），与药物B的函数关系相同，均为“g”。

公式组（式1）进一步扩展为预期相加效应的等效剂量计算公式组（式2），如下：

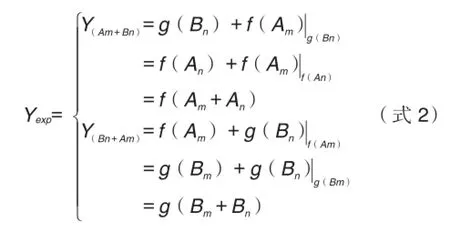
公式组（式2）中Bn和An是等效剂量，即g（Bn）=f（An）；Am和Bm是等效剂量，即f（Am）=g（Bm）。f（Am）|f（An）：在药物A的等效药效f（An）基础上，药物A沿着自己的量效曲线，前进Am剂量达到的药效增量；g（Bn）|g（Bm）：在药物B的等效药效g（Bm）基础上，药物B沿着自己的量效曲线，前进Bn剂量达到的药效增量。

规律3：两药的任一剂量组合（Am和Bn），预期相加效应值是一个连续的范围，边界值为Y（Am+Bn）和Y（Bn+Am），即为一个闭区间数集。在二维坐标图中，药效预期相加的量效关系显示为一条曲带，是一个闭区间数集函数。实际药效的量效关系显示为一条曲线（图3）。

任一剂量组合下（Am，Bn），预期相加效应值是一个连续的范围，在图上显示为一条红色直立线段，如图3中左图。将所有剂量组合下的预期相加效应值范围的线段连接起来，则成为一条曲带，称之为量效曲带，如右图，由2条曲线构成。黑色曲线为合用剂量的实际量效曲线。

预期相加效应的量效曲带构建公式（式3），如下。

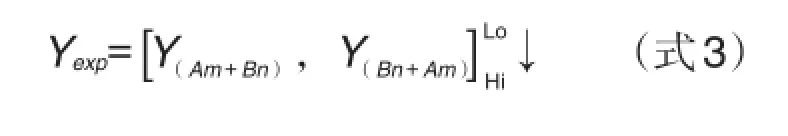
将公式组（式2），代入公式（式3），得出计算预期相加效应的通用展开公式（式4）

预期相加规律的扩展（三药以上合用）：多药合用相加效应值可分解为，在一个药物组合（或一个）预期相加药效水平的基础上，另一个药物（或一组）遵循自己的量效曲线（或量效曲带）前行到自身剂量达到的效应值。三药以上合用预期相加的量效曲带由多条曲线构成。

4.3 协同、相加及拮抗定义的扩展

根据上述对多药合用药效预期相加的数学规律的描述，药物合用预期相加效应的量效关系为量效曲带。可以进一步扩展和明确药效协同、相加和拮抗的定义。协同是实际药效大于预期相加效应范围，相加是实际药效在预期相加效应范围内，拮抗是实际药效小于预期相加效应范围（本文均是按照增函数的形式描述的）。

4.4 合用组效应值，在低于预期相加值，但又高于组合中最高的单药效应值

多药联合应用药物相加效应的规律的发现，实际上解决了合用组效应值大于单药效应值的评价问题。对于合用组效应值，在低于预期相加值，但又高于组合中最高的单药效应值时，本质上是一种拮抗效应，属于合用药效的降低。是否有实际应用意义，需要综合评价。

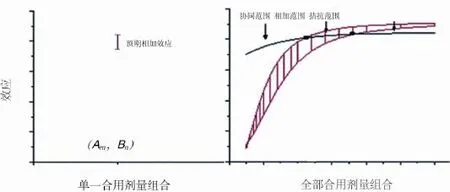
图3 量效曲带构成示意图.

5 两药合用药效预期相加数学规律的推导和求证

5.1 单用药物量效函数关系及剂量相加的特点

任何药物在有足够数量、能够涵盖效应窗口的剂量水平时（x1、x2、x3……xn），检测得出各自剂量水平的药效值（y1、y2、y3……yn），根据剂量值和效应值在二维坐标轴上的分布特征，均能够拟合出充分反映其量效特征的曲线和函数方程，拟合的量效曲线如图4，其量效方程可表示为方程式（式5）。

Y为药物效应，f为函数，X为药物剂量。

图4 单一药物的量效关系曲线图.

量效关系方程式（式5），有以下性质：

性质1：每个药物的量效关系均有其确定的函数和曲线特征。在确定的量效范围内，依据量效方程能推算剂量引起的药效值，即Y=f（X），根据药效值能推算剂量水平，即X=arc f（Y）。

药物剂量产生增量时，药效函数值也会发生改变。从性质1可得出，药物剂量为A1时，药物效应值为f（A1）。药物剂量为A1时，增加（或相加）剂量A2，药物相加效应值为剂量A1和A2之和的函数值，表达式为方程式（式6），如图5所示。

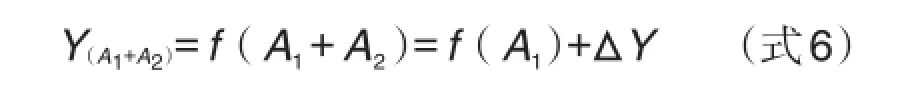
图5 单一药物自身剂量相加的量效曲线图.

从图5的几何分解可以看出，药物剂量增加到A2时，药物效应的增量ΔY，是以A1药效值为起点沿着其量效曲线前行，剂量增加到达A2时获得的增量，可表示为方程式（式7）。

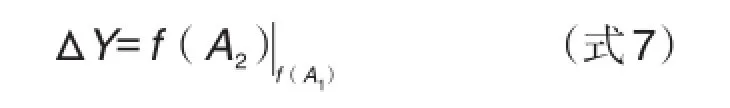
药物剂量A1和A2相加，药物剂量A2可视为剂量A1的增量，由图5可以得出性质2。

性质2：剂量增加所致的药效增量，符合量效函数方程，药效增量的幅度取决于剂量、量效曲线自身的特性和所在量效曲线的位置。

由方程（式7）代入方程（式6），可以得到方程式（式8）。

方程式（式8）可以得出性质3。

性质3：药物剂量A1和A2联合应用，两剂量的相加效应值，可分解为以f（A1）为起点、剂量A2沿着其量效函数曲线前行、达到自身剂量得出的效应值；反过来也成立。

即在相同的函数关系下，A1与A2是依次衔接的、可相加的药物剂量数值，为药物自身剂量相加所致药效相加的定义和计算方法。

5.2 两种不同药物合用时，药效相加的推导

5.2.1 将A1以下各剂量水平，均混合一定比例的赋形剂，命名为A′1系列剂量

加入赋形剂后，剂量增加，但药效值未增加，因而A′1以下剂量的量效曲线右移。药物A′1的量效函数关系，用Y=h（x）表示。图5的量效曲线则改变为图6所示。A′1以下各剂量系列的药物活性成分与A1以下对应各剂量的活性物质含量相等，因而药物效应值是不变的，有f（A1）=h（A′1）。因此，将其代入到方程式（式8），方程式（式9）是成立的。

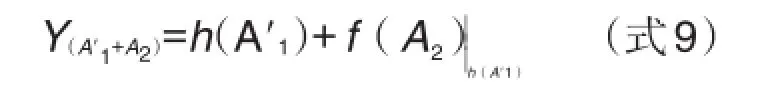
这时，因为A′1和A2的函数关系已经变得的不相同，A′1和A2则不是可依次衔接的、可相加的药物剂量数值，但A′1和A1是等效剂量。

图6 药物A1以下剂量加入赋形剂后，药物A和药物A′1的量效关系曲线.。。。。。。：药物A量效曲线的位置.

5.2.2 另有其他类型药物B，引起药物效应与药物A′1剂量系列相同，量效关系式表示为Y=g（X）

当剂量为B1时与药物A′1的药效相等，则存在g（B1）=h（A′1），将其代入到方程式（式9）；如果两药没有交互作用，仅有药效相加作用时，方程式（式10）是成立的，如图7所示。

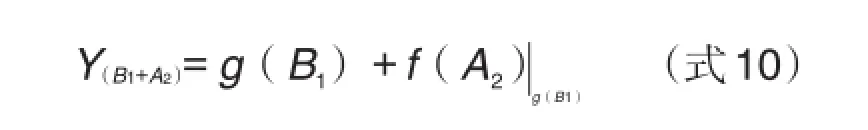
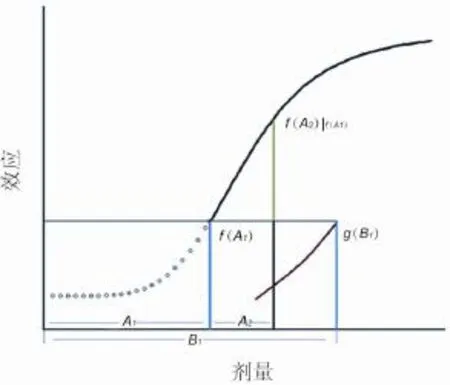
图7 药物A1以下剂量被等效药物B1取代后，药物A和药物B1效应相加的量效关系曲线.

方程式（式10）和图7中，因B1和A2的函数关系不同，B1和A2则成为不可衔接的、不可相加的药物剂量数值，但B1和A1是等效剂量。

5.2.3 性质4的推导

对方程式（式10）进行变量替换，令A2=Am，B1=Bn，可以推导得出性质4。

性质4：两种药物A和B，在任一剂量水平Am和Bn联合应用，两药相加效应值可分解为在Bn的药效水平g（Bn）的基础上，药物A遵循自己的量效曲线前行剂量Am达到的效应值，如图8A，方程式（式11）。或者，在Am的药效水平f（Am）的基础上，药物B遵循自己的量效曲线前行剂量Bn达到的效应值，如图8B，方程式（式12）。

f和g分别为药物A和药物B量效函数。

图8 药物A和药物B在任意剂量水平（Am和Bn）合用时，药效相加效应的量效曲线解析图.

该方法将两药的相加效应分解为一前一后的序贯效应。从解析量效曲线的角度来看，两药相加的药效值的计算，是将一个药物作为另一个药物效应的增量。

将图8A和图8B的2条量效曲线分别拆放到2个坐标图中，就会分别得到如同前面的图2中的上图和图2中的下图。因此，规律1得以证明。

5.2.4 两种不同类型药物合用时，药效相加计算的解决方法

药物A和药物B合用时，可因发生效应的次序（即序贯）不同，所致Y（Am+Bn）≠Y（Bn+Am）。这实际上构成了药物效应因给药序贯不同所致药效差异的数学基础。将Am与Bn变为依次衔接的、可相加的药物剂量数值，是计算两药合用相加效应的关键。从图8或图2可以看出，只有具备药物A和药物B各自的量效曲线函数，通过等效剂量的相互兑换，得到各自可遵循的自身量效函数曲线的起点剂量。

用与g（Bn）等效的f（An）进行兑换，方程式（式11）则变为相同的函数关系，如方程式（式13），An和Am的函数相同，依次相接，可以合并计算如下：

用与f（Am）等效的g（Bm）进行兑换，方程式（式12）则变为相同的函数关系，如方程式（式14），Bm和Bn的函数相同，依次相接，可以合并计算如下：

可以看出，如将其中一个药物设为目标药物（或参比药物），将另一个药物的剂量等效兑换为目标药物的等效剂量，等效剂量与目标药物剂量之和的函数值，即为预期相加效应的数值，故得出以下性质5。

性质5：两药在某一确定剂量合用时，一个药物剂量与目标药物进行等效剂量兑换后，预期相加量效曲线的函数关系与目标药物的函数关系相同；预期相加效应值为等效剂量与目标药物剂量合并的函数值。规律2得以证明。

显然，两药在某一确定剂量水平合用时，就会得出2个预期相加效应值。预期相加效应的量效关系为2个量效函数构成。

按照性质4，两药合用的相加效应可以分解为一个药物发生效应后，另一个药物在前一个药效基础上，沿着遵循自身的量效曲线前行，达到自身剂量所在的效应值。

由于药物的相加效应是零相互作用，因而联用的药物同时暴露于机体组织的每一个药效执行单位时，序贯前后的确定则必然是随机性的。

按照药效集合效应的特征，药物合用相加效应，实际是所有药效执行单位发生相加效应的总和。当所有的药效执行单位面对联用的两药暴露时，一部分执行单位表现的序贯行为Am→Bn，另一部分执行单位则是表现为Bm→An，两部分的比例是随机的，即每一个序贯方式面对的药效执行单位的数量是随机的。因此，预期相加效应值应在这个范围内是连续性的。

关于预期相加效应数值，会有以下性质：

性质6：两药在某一确定剂量合用时（Am和Bn），预期相加效应值是一个范围，即为一个闭区间数集。该数集的两个边界值，分别代表所有的药效执行单位为百分之百的Am→Bn序贯行为的预期相加效应值和百分之百的Bn→Am序贯行为的预期相加效应值，中间的数值范围为随机比例的Am→Bn序贯行为和Bn→Am序贯行为的药效执行单位药效的累积之和。预期相加效应值落在该数集范围内，数据是连续的。以合用组的每个剂量组合点为横坐标，效应值数集为纵坐标可得到的量效函数关系为闭区间数集函数，显示为一条曲带。规律3得以证明，用方程式表示如下：

将方程式（式13）和（式14）代入该方程式（式15），得到通用展开公式（式4）展开得以推导完成，如下：

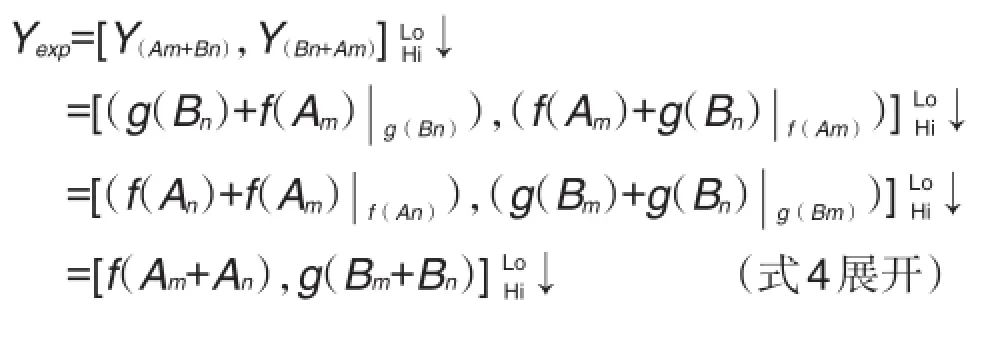
6 三种以上药物合用药效预期相加数学规律的推导和求证

6.1 求证三药合用、预期相加效应的药效值和构成量效曲带的量效曲线

两药合用时，药效相加是在一个药物效应基础上，另一个药物沿着自己的量效曲线达到自身剂量的药效水平；药物序贯不同造成的差异，2条量效曲线构成了相加效应的量效曲带。

三药合用时，基于规律1进行推导，三药合用药效相加是在任意两药相加效应基础上，第三个药物沿着自己的量效曲线达到自身剂量的药效水平，即该组合药物的相加效应与第三个药物的量效曲线进行等效剂量兑换后，该等效剂量与第三个药物剂量合并，遵循第三个药物的量效关系函数得出的函数值（符合规律2），即为三药合用预期相加效应值。

反过来也成立，基于规律1进行推导，在一个药物效应基础上，另外任意相加的2药沿着自身相加效应的量效曲线达到自身剂量的药效水平（符合规律2）。

药物A、药物B和药物C三药合用，任一剂量水平Am，Bn和Co合用剂量。任何一剂量组合则有三种不同的2+1组合，分别为（Am+Bn）+Co，（Am+Co）+Bn和（Bn+Co）+Am。以（Am+Bn）+Co组合方式为例，对其预期相加效应进行一般公式解析，展开式（式16）如下所示。

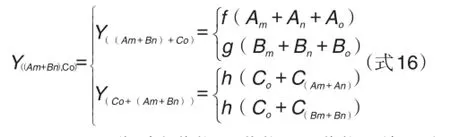
f，g和h分别为药物A、药物B和药物C单用时的量效关系函数式

上述两药合用（Am+Bn）产生相加效应的量效关系为2条相加量效曲线构成的量效曲带，即每个合用剂量值产生的药物预期相加效应值为2个边界数值，即f（Am+An）和g（Bm+Bn）。因此，在两药某一剂量水平相加效应基础上，第三个药物沿着自己的量效曲线达到自身剂量的药效水平时，则为2个药效值，即f（Am+An+Ao）和g（Bm+Bn+Bo）；反过来也成立，即在一个药物某个剂量药效水平时，另外2个药物沿着各自相加效应的量效曲线构成的量效曲带，达到自身剂量的药效水平时，也为2个药效值，即h（Co+C（Am+An））和h（Co+C（Bm+Bn））。每种2+1组合方式的预期相加效应量效曲带有2×1×2=4条曲线构成。

因此，预期相加效应的量效关系，三种药物合用，三种不同的2+1组合，在二维坐标系中，显示为4×3=12条曲线围成的量效曲带，展开式显示如下：

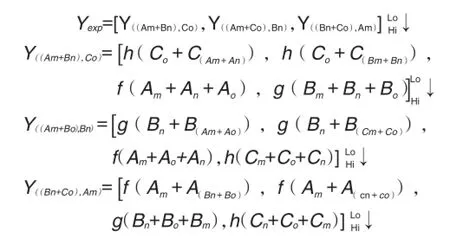
合并以上各个函数方程，可得（式17）：

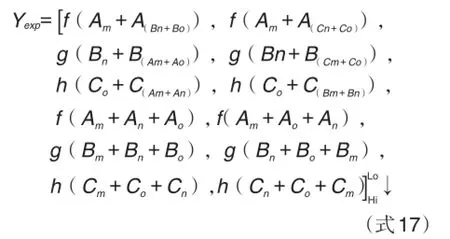
因此，该数集是由12个单元构成，每个合用剂量水平预期相加效应数值的取值范围是由这12个单元数值的最小者和最大者确定的。

6.2 求证四药合用、预期相加效应的药效值和构成量效曲带的量效曲线

6.2.1 三个药物组合+另一个药物（3+1组合）

基于规律1进行推导，在任意三药合用的产生的相加药效基础上，第四个药物沿着自身的量效曲线前行达到自身剂量的药效水平；反过来也成立，在一个药物药效的基础上，任意合用的三个药物沿着自身的相加效应量效曲线构成的量效曲带，达到各自的等效相加剂量时的药效水平。

以药物A、药物B、药物C和药物D四个药物为例，任一剂量联用方式共有4种组合，（Am+Bn+Co）+Dp，（Bn+Co+Dp）+Am，（Co+Dp+Am）+Bn和（Dp+Am+Bn）+Co。每一个三药组合有12条预期相加曲线，序贯方式的不同，则有12×1×2=24条相加曲线，四种组合合计有24×4=96条预期相加曲线。

6.2.2 两个药物组合+另外两个药物组合（2+2组合）

基于规律1进行推导，在任意两药合用产生的相加药效基础上，另外两药合用沿着自身的相加量效曲带前行达到自身的等效相加剂量时的药效水平。四药合用的组合有（Am+Bn）+（Co+Dp），（Am+Co）+（Bn+Dp）和（Am+Dp）+（Bn+Co）。每个两药组合有2条预期相加曲线，序贯方式不同，则有2×2×2=8条相加曲线，三种组合合计有8×3=24条预期相加曲线。

四种药物合用时，预期相加效应的量效曲带则有96+24=120条预期相加效应曲线构成。

因此，该数集是由120个单元构成，每个合用剂量水平预期相加效应数值的取值范围是由这120个单元数值的最小者和最大者确定的。

6.3 求证五药以上合用、预期相加效应的药效值和构成量效曲带的量效曲线

6.3.1 四个药物组合+一个药物

基于规律1进行推导，药物A、药物B、药物C、药物D和药物E五个药物，共有5种4+1组合，包括（A+B+C+D）+E，（B+C+D+E）+A，（C+D+E+A）+B，（D+E+A+B）+C和（E+A+B+C）+D。按照以上方法计算，每种120×1×2=240条，5种组合共240×5= 1200条预期相加曲线。

6.3.2 三个药物组合+两个药物组合

基于规律1进行推导，共有10种3+2组合，包括（A+B+C）+（D+E），（A+B+D）+（C+E），（A+B+E）+（C+D），（A+C+D）+（B+E），（A+C+E）+（B+D），（A+D+E）+（B+C），（B+C+D）+（A+E），（B+C+E）+（A+D），（B+D+E）+（A+C）和（C+D+E）+（A+B）。

每个三药组合有12条预期相加曲线，每个两药组合有2条相加曲线，结合序贯不同，每个3+2组合有12×2×2=48条预期相加曲线。10个组合合计为48×10=480条相加曲线。

五种药物合用时，预期相加效应的量效曲带则有1200+480=1680条预期相加效应曲线构成。

因此，该数集是由1680个单元构成，每个合用剂量水平预期相加效应数值的取值范围是由这1680个单元数值的最小者和最大者确定的。

6.3.3 六药合用

六药合用预期相加效应的量效曲带的计算，按照上述方法以此类推，6个5+1组合，（1680×1×2）× 6=20 160；15种4+2组合，（120×2×2）×15=7200；10种3+3组合，（12×12×2）×10=2880；合计20 160+7200+2880=30240条预期相加曲线。

6.3.4 七药合用

七药合用，预期相加效应的量效曲带的计算，按照上述方法以此类推，7个6+1组合，（30240×1× 2）×7=423360；21个5+2组合，（1680×2×2）×21= 141120；35个4+3组合，（120×12×2）×35= 100800。合计423360+141120+100800=665280条预期相加曲线。

6.3.5 八药以上合用

八药以上合用，预期相加效应的量效曲带的计算，按照上述方法以此类推，数量呈指数性增长。

6.4 三种以上药物合用预期相加效应的总结

归纳上述三药以上合用时预期相加效应的数学规律，在两药合用规律基础上的扩展应用，可将规律1的扩展为，在一个药物剂量组合预期相加效应的基础上，另一个剂量（或剂量组合）沿着自身量效曲线（或者量效曲带）达到各自剂量时的效应值。预期相加效应的量效曲带由每个合用剂量组合产生的多个单元数值的最小者和最大者构成。

7 多药合用药效协同、相加和拮抗的定量计算指标

7.1 协同、相加和拮抗的剂量范围

实际量效曲线位于相加量效曲带上方的区段为协同剂量范围，与相加效应曲带重合的区段为相加剂量范围，位于相加量效曲带下方的区段为拮抗剂量范围。通过图形测定，或者计算合用剂量实际量效曲线方程和合用剂量预期相加量效曲带方程组成的方程组，定量计算得出药物合用产生协同、相加和拮抗的剂量范围。

7.2 基于剂量的合用指数（combination index based on dose，CId）

在某一确定的剂量水平下，实际药效值（Yobs）分别与相加药效值范围两个边界值（Yexp-min和Yexp-max，即预期相加效应值范围内的最小值和最大值）进行比较，分别得到CId1和CId2（式18）。

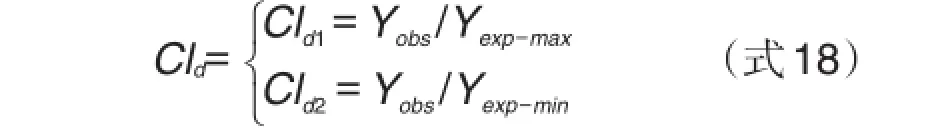
判断标准为协同：CId1>1，CId2>1；相加：CId1≤1，CId2≥1；拮抗：CId1<1，CId2<1。

7.3 基于药效的合用指数（combination index based on effect，CIe）

在某一确定效应下（如ED50和ED90），实际合用剂量（actual dose，D）分别与预期相加药效剂量（expected doses，Dexp）范围的2个边界值（Dexp-min和Dexp-max）进行比较，分别得到CIe1和CIe2（式19）。

判断标准为协同：CIe1<1，CIe2<1；相加：CIe1≤1，CIe2≥1；拮抗：CIe1>1，CIe2>1。

7.4 说明

CId和CIe的结论是一致的，可选择其一进行计算。两药合用时，预期相加效应范围的边界值分别为f（Am+An）和g（Bm+Bn）；三药以上合用时，则有较多个预期相加效应值，需要排序比较，找出最小值（Yexp-min）和最大值（Yexp-max）作为边界值。

8 特殊情况的应对方法

上述的数学推导和求证过程，均按照多药合用剂量在各单药共同的量效范围内进行，描述的函数形式均为增函数。但在实际应用过程中还会遇到一些特殊状况，表现为预期相加的量效关系为1条曲线，均需按照上述数学原则处理即可，简述如下：

8.1 药物A有活性，药物B无活性，药物A与药物B联用后，药物A量效曲线发生改变

将药物A作为目标药物，药物B的效应值为零（或者药物B最大药效低于药物A的量效范围），药物联合应用的预期相加效应仅为1条曲线方程，与药物A单药的量效曲线一致（即量效曲带仅有源自药物A量效方程的数据）。合用组实际效应值高于预期相加效应值为协同（CId>1），等于预期相加效应值为相加（CId=1），小于预期相加效应值为拮抗（CId<1）。

8.2 药物A和药物B均无活性，药物A与药物B联用后有活性

药物A和药物B的单药无效，即量效曲线均为Y=0，因此，两药联合应用预期相加效应曲线为Y=0。药物合用实际量效关系曲线方程Y=ƒ（X）>0与预期相加效应曲线方程Y=0的比较，CId数值为无穷大（+∞），药物A和药物B在其剂量范围内合用，恒为协同效应。

8.3 预期相加效应的量效曲带缩并成一条曲线

量效曲带缩并成1条曲线，如为两药合用，此时则是Y（Am+Bn）=Y（Bn+Am）。每个合用剂量组合的预期相加效应则为1个数值点。合用组实际效应点高于该曲线时（CId>1），则为协同；与该曲线重合时（CId=1），则为相加效应；低于该曲线时（CId<1），则为拮抗。此种情况下，可推导出Loewe的等效线模型法（x/DA+y/DB=1，证明过程略）。

8.4 仅有一个单药的量效曲线

仅有一个单药的量效曲线时，如果合用的药物有药效（且无法获得单用药的量效曲线时），这样仅能获得量效曲带中的1条预期相加的量效曲线。因不能判断该曲线处于预期相加效应量效曲带中的位置，合用组实际效应点高于该曲线时（CId>1），则为相加+协同；与该曲线重合时（CId=1），则为相加效应；低于该曲线时（CId<1），则为相加+拮抗。

8.5 给药方式为序贯给药

仅选取与给药序贯方式一致的预期相加效应的量效曲线，进行协同、相加或拮抗的定量计算，但需注意序贯给药的时间间隔作为区分要素。

基于上述，多药合用预期相加的量效关系，在二维坐标图中有时会出现预期相加的量效曲带连接1条预期相加的量效曲线。

9 讨论和评价

关于药物的联合应用，历史非常悠久。从传统中药联合用药的历史来看，商汤时代古人就发现了药物配伍的奥妙；从黄帝内经开始，中医用药就告别了单枪匹马时代。在一些中医著作中收录的各类固定配伍方子的数量占有相当大的比例，很多都是几十味药组成的大方子。组方遵循的联合用药指导线，则有君臣佐使、七情和合、十八反、十九畏等，这些作为指导中医用药的理论已有上千年历史。

对联合用药的定量计算方法，则是1871年Fraser首次用图解法表征两个药物的相互作用；1926年Loewe将其规范，并用等效线法表征两药的相互作用关系，已经有100多年。人们在此基础上发展了几十种计算方法。有许多学者在发展新的计算方法方面进行了尝试和挑战，国外学者如Chou［15-16］，Berenbaum［14］，Greco等［5］，Lee等［17-18］和Tallarita［19］等，国内学者如孙瑞元和金正均等［3，20］。

为何还是有一些学者认为，这些方法经常相互矛盾，同一组数据用不同的方法处理，常会得出不同的结论。为何还是有学者认为，没有方法就是唯一的方法。有些干脆抛开这些计算方法，采用直接进行简单药效比较的方法。

人们对于自然科学的了解和学习大多从数学开始，近代科学正是在追寻自然界的数学规律中取得长足进步的，许多重大突破都是基于数学的发展。马克思曾说过，一种科学，只有在成功地运用数学时，才算达到了真正完善的地步。数学方法成功地融入或运用于一种科学的标志，必须具有以下基本特征：高度的抽象性、严密的逻辑性、应用的广泛性和描述的精确性［21］。

药理学发展之初，就融入了数学方法。在定量单药的药效、毒性、体内外动力学过程以及阐明药物作用机制等方面均形成了一系列成熟的理论、方法和模型，促进了药理学的发展、进步和成熟。但在多个药物合用、相互作用进行定量评价方面，长期以来是处于繁杂混乱状态的，总有一些找不到北的感觉。

数学起源于远古时代，物物交换发展了的结绳计数和划痕计数，土地丈量促进了几何的发展。后来出现了数轴、实数的概念和加减的运算法则。大家都知道，任意2个实数a和b，是可以相加的，a+b的和一定是实数，其结果是沿着数轴线的叠加，如1+1=2和50+60=110等，每个实数所在的数轴都是一样的。加法运算法则有交换律a+b=b+a，也有结合律a+（b+c）=（a+b）+c等。对于产生药效的多个药物合用，人们常常习惯于用简单的加法运算法则思考问题，很自然地认为药效值为1的两个药物合用，药物相加效应值为“1+1=2”，协同是“1+1>2”，拮抗是“1+1<2”。但是，如果一个药物的效应值为50%的抑制率，另一个药物的效应值为60%的抑制率，如果认为两药合用的结果是110%的抑制率，则是非常不合适的。任何数学大厦都是建立在最基本的、如同“1+1=2”之类的基石之上的。药物合用效应定量评价的混乱现状，很可能是最基本的、如同“1+1=2”之类的基石出现了问题。

通过前述的推导演算可以看出，药物合用所致的药效相加是有其特有的内在规律的，它遵循的是药物量效关系曲线，遵循的是药物反应性的基本规律，遵循的是药物效应的集合规律。每一个药物的作用方式、量效曲线是不一样的；每个药物的效应是药物作用于每一个药效执行单位，每个执行单位活性之和构成了总的药效。由于药物合用组合的不同和给药顺序（序贯）的不同，因而导致药物效应相加数值是不一样的，数值的大小取决于在量效曲线的位置。

正如上述判断抑制率为50%（药物A）和抑制率为60%（药物B）的两药合用时的抑制率为110%，显然是不合适的。同样，作用方式不同、药效为1的两种药物合用时，认为“1+1=2”的结论也是非常不妥的。按照前述的预期相加的数学规律1～3的描述，多药合用药效相加的结果，不是一个单个的效应值，而是一个数据集合，相加效应测定值则是落在该数据集合的范围内。同样，在某一确定的效应下，属于预期相加作用的剂量也是一个剂量范围，而不是一个单一的剂量值。

这样就会清楚以往前辈学者们困惑的原因。以往学者们建立的这些计算方法，多数均采用了等效剂量的处理方法。但在进行等效剂量处理后，预期药效相加值出现的不一致的现象，无法作出进一步的解释，因而在数学推导上成为了一道不可逾越的障碍，也就无法进一步地推导得出经过等效剂量处理后的数学规律。也只能在特定条件下，如一个药物是另外一个药物的稀释物时，得出的合用量效曲线分析，能够经得起严格的数学推导。如果将这种在特定条件下、产生的特解数学公式外推，在面对复杂的、作用方式迥异的药物合用，进行相互作用的定量分析时，必然会得出令人困惑的结论。

造成这种结果的原因，是前辈学者们在进行数学推导时没有关注药理学中的2条铁律。一条铁律是药物效应受机体组织状态的影响，该铁律外推到多药的相互作用，则体现为药物序贯特性。另一条铁律是药效的集合特性。这种序贯特性和集合特性，以及药物相加的零相互作用特性，决定了多药合用时每一个药效执行单位面临的多药暴露的序贯方式是一个随机现象，因而预期相加效应不是一个确定的数值，而是一个范围，在这个范围内数据是连续的。

因此，作者所建立的方法，首先通过归纳出药物相互作用时多药合用量效关系数据的4个特点，以此为基础，将共同的药效作为评价目标，这样就能实现高度的概括和抽象，经得起数学和药理学严密的逻辑推导；其数学表达式是由一般数学函数推导得出，如Y=f（X）和Y=g（X）等，该方法具有通用性的特征，能够对多个以上药物合用或不同方式合用的预期相加效应的计算实现外推，因而具有应用的广泛性；通过比较预期相加量效关系曲带和实际量效曲线，则能够实现协同、相加、拮抗及其程度的精确计算，达到了描述的精确性。

基本结论就是多药合用预期相加效应的量效关系是一个闭区间数集函数，在二维坐标系中表现为一条量效曲带。基本计算步骤包括：①拟合单药各自的量效曲线和量效方程；②依次序贯对各合用剂量水平进行等效剂量兑换，计算预期相加的函数值；③重构预期相加量效曲带的量效曲线和拟合曲线方程；④比较预期相加效应量效曲带和实际量效曲线的位置关系，计算相关指标，包括协同剂量范围、相加剂量范围和拮抗剂量范围，剂量合用指数和效应合用指数等，各种情况下的计算实例、处置技巧和相关数学推导等参见［22］。本文仅提供一个简单实例，来说明计算步骤，见补充材料。

该方法又称为基于自身剂量增量相加的序贯兑换及量效曲带重构法（The sequential dose exchange based on self-increment-addition and remodel of dose-effect belt，Dose Exchange& Belt）。因为多药合用预期相加效应在二维坐标图上显示为一条曲带，合用组的实际量效关系为一条曲线，而呈现“一条带和一条线”现象，可形象地称为“一带一线法”（one belt and one line method）。

10 结语

本方法的建立是数学量效关系函数与药理学特征的合理契合和推导，表现为4个方面：①对各单药量效关系曲线的几何解析，将不同药物效应相加解析为一个（或一组）药物效应与另一个（或一组）药效增量的顺序相加，契合了药物序贯特征的药理学规律，同时也解释了药物相加效应的值域范围和闭区间边界；②与药物集合效应特征的契合，解释了值域区间内数据的连续性；③等效剂量兑换后，药物相加效应的函数规律，可解释能够实现对多种药物合用产生协同、相加和拮抗定量计算的合理性。三者结合起来，则能完美实现多种药物联合应用效应改变的定量计算。④由此外推，多药合用相加效应的计算，对于作用方式不同，药效为1和药效为2的药物来说，1+1≠2、1+2≠3、1+2≠2+1是常态，而1+1=2、1+2=3和1+2=2+1是特例。即在药物联用领域，遵循的是如同1+1≠2、1+2≠2+1的思维模式，有别于传统的、如同1+1=2的思维模式。

药物效应评价的基本原则是随机、对照、均衡和重复。本方法对预期相加量效曲带的计算，本质上是药物联用时，基于单用药的量效关系计算推导出的联合用药对照组的量效关系，是一种预期的量效关系。

补充材料——两药合用的计算实例

本计算实例，仅描述计算方法的实施步骤。研究背景、立题依据、实验操作步骤等，未做详细描述。多药合用药效计算方法，还有多方面令人关注的问题，如拟合函数方程的选择、如何有效合理地进行曲线拟合、判断拟合量效曲线方程的合理性、如何选择联用各药物的剂量配比、如何将统计分析纳入到分析之中、计算结果与实际意义相关性的判读等，此处均未讨论和评价。

题目：硝羟基喹啉（nitroxoline，NX）为抗感染药，近年发现具有靶向抗癌活性，CFDA已批准进入临床试验。紫杉醇（taxol，TX）是常用抗癌药物。以NX/TX联合应用，MTT法检测抑制人肝癌细胞HepG2生长。计算NX和TX按固定比例合用时，药效协同、相加及拮抗的相关指标。

计算步骤

步骤1制作各单药和合用组各剂量水平的量效关系表，拟合各自的量效关系曲线方程

NX和TX各自单药的量效关系数据、NX+TX按固定比例合用（1∶1，mg·L-1+μg·L-1）的量效关系数据（表1）。

绘制药物NX和药物TX单用的量效曲线图，以合用组中药物NX为自变量绘制合用组的量效曲线图（图1）。

用Logistic模型法拟合得出的曲线和量效方程，有较好的拟优合度，故可选定作为本实验的曲线拟合方程。拟合出各自单药的量效关系方程，分别为：

单用药物 NX：Y=（4.3188-94.209）/{1+（X/1.9981）^3.0815}+94.209，函数记为Y=f（X）（式1）

表1 硝羟基喹啉（nitroxoline，NX）和紫杉醇（taxol，TX）单用及合用的量效关系数据

图1 NX和TX单用及合用的量效关系曲线拟合图.

单用药TX：Y=（0.8779-92.1626）/{1+（X/ 2.8494）^1.7569}+92.1626，函数记为Y=g（X）（式2）

合用组中以NX为自变量的量效关系方程为：

步骤2等效剂量序贯兑换，计算合用条件下构成预期相加药效的各个量效关系数值

将NX和TX分别作为目标药物，序贯进行等效剂量兑换后合并剂量值（表2）。

表2内容，展示的是实际药物合用各浓度点的等效浓度值、预期相加效应值和实际观察的药效值，计算得出了剂量合用指数（CId1和CId2），可以看出药物合用低浓度的4个合用组合的实际药效与预期相加量效范围进行比较，高浓度的2个合用组合的实际药效与预期量效单值进行比较。NX+TX合用的0.5+0.5（mg·L-1+μg·L-1）和16+16（mg·L-1+μg·L-1）合用组为协同，其余各合用组为拮抗。

步骤3重构预期相加效应的量效曲带、拟合量效曲线和曲线方程

预期相加效应的量效曲带，本质上根据单用药的量效关系方程计算推导出的联合用药对照组的量效关系，是一种预期的量效关系，能够计算出所有剂量组合的预期相加效应范围。

根据计算需求，可用实际合用剂量进行计算；或者为提高预期相加效应曲带的拟合精度，可在每个合用剂量组合之间插入数个中间剂量值，进行计算。然后基于单用药的量效关系方程，计算每个剂量点的预期相加量效关系曲带的边界值f（Am+An）和g（Bm+Bn）。本组数据每个剂量间隔设置了3～4个插值，如0.5+0.5与1+1之间，增加了0.6+0.6，0.7+0.7，0.8+0.8，0.9+ 0.9等，按照表2的计算方式进行计算（表3）。

以合用组的NX各剂量水平为横坐标，分别以各预期相加效应值f（Am+An）和g（Bm+Bn）为纵坐标作图，构成预期等效相加效应的量效曲带。同时按照方程式（式3）Y=（15.8595-94.9017）/{1+（X/ 1.7190）^2.4490}+94.9017，在该图上作出合用组实际效应的量效曲线，如图2。

图2 NX和TX固定比例（1∶1，mg·L-1+ μg·L-1）的两药合用的预期相加量效曲带和实际效应量效曲线图.

将合用组中NX剂量与NX为目标药的预期相加效应值f（Am+An）进行量效方程拟合，合用组中NX剂量与TX为目标药的预期相加效应值g（Bm+Bn）进行量效方程拟合，得到围成预期相加效应量效曲带的2条曲线方程，分别为：

表2 NX和TX分别作为目标药序贯等效剂量兑换后，预期相加效应值和CId

表3 NX和TX按固定比例合用，计算不同合用剂量水平构成的量效曲带的预期相加效应值

以NX为目标药：

以TX为目标药：

步骤4比较合用组预期相加效应量效曲带和实际量效曲线的位置关系，计算相关指标

1 目测结果

从图2可以看出，在合用浓度点0.5+0.5（mg·L-1+ μg·L-1）到6+6（mg·L-1+μg·L-1）范围内，预期相加效应呈现为量效曲带。0.5+0.5（mg·L-1+μg·L-1）位于量效曲带上方，呈现协同效应；合用剂量点1+1，2+2和4+4（mg·L-1+μg·L-1）位于量效曲带下方，呈现拮抗效应。

合用剂量点6+6（mg·L-1+μg·L-1）到16+16（mg·L-1+μg·L-1）范围内，预期相加效应的量效关系，仅为一条预期相加效应曲线。合用剂量点8+8（mg·L-1+μg·L-1）位于量效曲线下方，为拮抗；16+16（mg·L-1+μg·L-1）位于量效曲线上方，为协同。

2 计算协同、相加和拮抗的剂量范围

将上面两个方程式，分别与实际效应的量效方程构成方程组，求解：

方程组1：

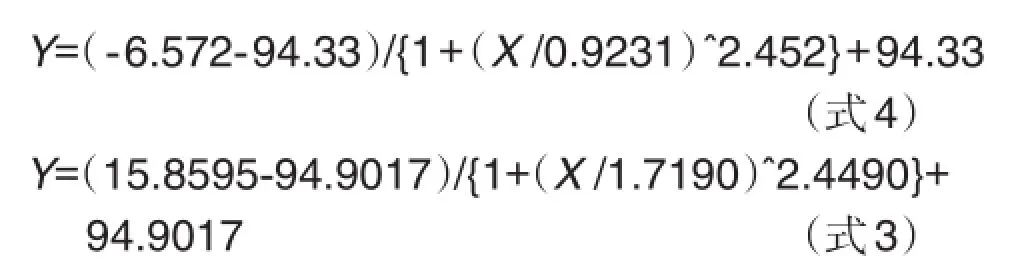
方程组2：

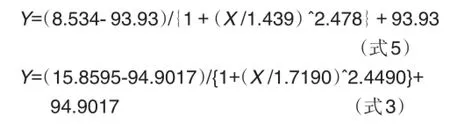
解方程组1，得出：

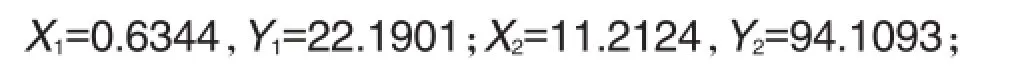
解方程组2，得出：

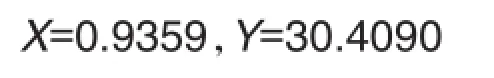
NX和TX在共同的效应范围内，预期相加为一条量效曲带，得出相加效应的NX浓度范围的边界值是0.6344和0.9359 mg·L-1。NX和TX在共同的效应范围之外，预期相加效应量效关系是一条曲线，即有一个相加NX浓度效应点11.2124 mg·L-1。根据NX与TX的组合比例关系，很容易得到伴随的TX相加效应的浓度。结果如下：

协同效应剂量范围（NX+TX）：

相加效应剂量范围（NX+TX）：

拮抗效应剂量范围（NX+TX）：

合用组实际效应量效曲线中属于相加效应的范围是：22.1901%～30.4090%，94.1093%。

3 计算CId

从表2可以看出，在合用浓度点0.5+0.5（mg·L-1+ μg·L-1）：预期相加效应值分别为14.1820和11.5444，实际观测值为19.7。CId1为19.7/14.1820=1.3891>1，CId2为19.7/11.5444=1.7065>1，协同。

其余各合用浓度点的计算方法相同，结果见表2。

4 计算CIe

可选定任一药效水平，如ED50。在图2的纵坐标为50%处，作一平行于横轴的直线，分别与等效量效曲带和实际量效曲线交点于A，B和C点，分别得到横坐标点为1.0196，1.4059和1.5370，如图3。因此，在药效ED50处，预期相加效应的剂量范围点（NX+TX）为1.0196+1.0196（mg·L-1+μg·L-1）和1.4059+1.4059（mg·L-1+μg·L-1），实际效应的剂量点（NX+TX）为1.5370+1.5370（mg·L-1+μg·L-1），位于量效曲带的下方。

图3 合用组预期相加量效曲带、实际量效曲线在ED50处的交点图.

计算CIe1和CIe2，分别为CIe1=1.5370/1.4059= 1.0932>1，CIe2=1.5370/1.0196=1.5074>1，提示为拮抗。

计算步骤结束。

［1］Chou TC.Theoretical basis，experimental design，and computerized simulation of synergism and antagonism in drug combination studies［J］.Phar⁃macol Rev，2006，58（3）：621-681.

［2］Berenbaum MC.What is synergy？［J］.Pharmacol Rev，1989，41（2）：93-141.

［3］Zheng QS，Li JC，The dynamics of drug interaction［M］∥Sun RY，Zheng QS.The New Theory on Math⁃ematicd Pharmacology（数学药理学新论）Beijing：People′s Medical Publishing House，2004：131-184.

［4］Fraser TR.An experimental research on the antag⁃onism between the action of physostigma and atro⁃pia［J］.Proc R Soc Edin，1871；7：506-511.

［5］Greco R，Bravo G，Parsons C.The search for synergy：a critical review from a response surface perspective［J］.Pharmacol Rev，1995，47（2）：331-385.

［6］Xu DZ.Evaluation in drugs combination［J］.Prog Physiol Sci（生理科学进展），1992，23（3）：248-253.

［7］Loewe S，Muischnek H.Über kobinationswirkugenⅠ.Hilfsmittel der fragestellung［J］.Arch Exp Path Pharmak，1926；114：313-326.

［8］Loewe S.Die quantativen probleme der pharmakologie［J］.Ergeb Der Physiol，1928，27（1）：47-187.

［9］Loewe S.Antagonisms and antagonists［J］.Phar⁃macol Rev，1957，9（2）：237-242.

［10］ Tallarida J.Quantitative methods for assessing drug synergism［J］.Genes Cancer，2011，2（11）：1003-1008.

［11］ Tallarida J.An overview of drug combination analysis with isobolograms［J］.J Pharmacol Exp Ther，2006，319（1）：1-7.

［12］ Bliss CI.The toxicity of poisons applied jointly［J］.Ann Appl Biol，1939，26（3）：585-615.

［13］Geary N.Understanding synergy［J］.Am J Physiol Endocrinol Metab，2013，304（3）：E237-E253.

［14］Berenbaum C.The expected effect of a combina⁃tion of agents：the general solution［J］.J Theor Biol，1985，114（3）：413-431.

［15］Chou TC，Talalay P.Analysis of combined drug effects：a new look at a very old problem［J］.Trends Pharmacol Sci，1983，4（11）：450-454.

［16］Chou TC.Drug combination studies and their synergy quantification using the Chou-Talalay method［J］.Cancer Res，2010，70（2）：440-446.

［17］Lee JJ，Kong M.Confidence intervals of interac⁃tion index for assessing multiple drug interaction［J］.Stat Biopharm Res，2009，1（1）：4-17.

［18］Lee JJ，Lin HY，Liu DD，Kong M.Emaxmodel and interaction index for assessing drug interaction in combination studies［J］.Front Biosci（Elite Ed），2010，2（5）：582-601.

［19］ Tallarida J.The interaction index：a measure of drug synergism［J］.Pain，2002，98（1/2）：163-168.

［20］Jin ZJ.Addition in drug combination［J］.Acta Phar⁃macol Sin（中国药理学报），1980，1（2）：70-76.

［21］Zhang GQ.Talking about mathematics profession［J］.Shuxue Tongbao（数学通报），2009，48（7）：1-7，36.

［22］Yuan SJ.The Mathematical Laws of the Expected Additive Effect in Multi-drug Combination and the UniversalMethodforQuantitativelyCalculating Synergism and Antagonism（多药合用药效相加的数学规律及协同拮抗的定量计算方法）［M］.Nanjijng：Phoenix Science Press，2016：53-105.

Establishment of new method for quantitatively calculating synergistic,additive and antagonistic effect in multipledrug combination

YUAN Shou-jun
（Laboratory of Toxicology and Tumour Pharmacology,Institute of Radiation Medicine,Academy of Military Medical Sciences,Beijing 100850,China）

Given the complexity of diseases and etiology of multiple targets and links，therapies with multi-drug combination towards multiple targets are better options for treating serious diseases，such as cancer，than a single-target medicine.Multi-drug combination may cause interactions at different levels，but the efficacy of these drugs manifests itself as synergism，addition or antagonism.Because there is no reliable quantitative method for synergism，addition and antagonism that can simultaneously withstand double test of mathematics and pharmacology，the development of novel drug combinations has come to a standstill.By exchanging the equivalent doses and introducing two basic principles that have been long neglected in the pharmacological field（the sequential principle for multi-drug use and the collective property of efficacy）into the geometrical analysis of the dose-effect relationships，the author has found the mathematical laws for the expected additive effect in multi-target drug combina⁃tion，and worked out a universal formula.The dose-effect relationship of the expected addition is a number set function of multi-drug combination doses with a closed interval，which performs as a belt in a two-dimensional coordinate，while the actual observed one presents as a curve.The number of curves that constitute the belt increases exponentially whith the incnease of combined drugs.By solv⁃ing the equation groups composed of the belt and the curve，related parameters in multi-drug combina⁃tion can be precisely calculated，such as dose ranges of synergism，addition and antagonism，as well as combination indexes based on dose and one based on efficacy，which will also provide a quantita⁃tive analysis method for interactions between various factors in biological systems.

multiple-drug combination;drug interaction;quantitative evaluation;expected additive effect;dose-effect belt;synergism;addition;antagonism;one belt and one line method

YUAN Shou-jun，E-mail：ysj_yuan@139.com

R969.2

A

1000-3002-（2016）12-1316-17

10.3867/j.issn.1000-3002.2016.12.011

2016-11-23接受日期：2016-12-15）

（本文编辑：齐春会）

袁守军，E-mail:ysj_yuan@139.com