船用光学陀螺动态随机误差特性分析方法

魏建仓，郭岳山，刘东娜

（天津深之蓝海洋设备科技有限公司，天津300457）

船用光学陀螺动态随机误差特性分析方法

魏建仓，郭岳山，刘东娜

（天津深之蓝海洋设备科技有限公司，天津300457）

惯性技术是舰船自主获取运动方位、姿态信息的重要方法之一，而激光和光纤陀螺已成为惯性导航、制导和动态精确测量的核心元器件，研究其随机误差特性对于提高舰船作战和测量具有非常重要的意义。介绍了光学陀螺随机误差特性和基于统计特性的随机误差分析方法，为更有效地测试和分析时变噪声环境下的陀螺特性，采用Allan方差（Avar）和动态Allan方差（DAVAR）来识别和分析陀螺输出数据。对比分析了纯白噪声特性和光纤陀螺实验数据中随机噪声类型和水平的辨识结果。结果表明，DAVAR能对光学陀螺长时间运行下的时变噪声特性进行有效识别和分析，准确地反映陀螺的动态特性。

惯性导航系统；光学陀螺；随机误差特性；方差分析；DAVAR

激光陀螺（RLG）和光纤陀螺（FOG）统称为光学陀螺，基本工作原理相似，均利用Sagnac效应测量载体的旋转角速度。不同之处主要表现在FOG利用了线圈替代了环形激光器。

随着导航技术的快速发展，作为核心元器件，光学陀螺仪在船舶惯导、制导领域得到了普遍应用。其精度基本决定了惯性导航系统（INS）的精度［1］，因此研究其随机误差具有非常重要的意义。

舰船运行的主要特点是航行时间长，因而INS和陀螺仪长期处在工作状态。陀螺仪的随机漂移会造成发散的角度误差，且时间越长，发散程度越严重。因此在船用光学陀螺仪的研制和使用过程中，必须对其性能进行测试、分析和评估，然后通过适当的手段进行误差补偿［2］提高精度。相比于其他用途的陀螺仪，船用陀螺仪的设计和使用更需重视随机误差的影响。

现有的对陀螺随机漂移进行描述的方法包括RMS（均方根）和N秒平均法，且均已得到广泛应用，但其与相关时间结合时并不能完全预测系统的性能。在统计学意义上，均值和方差能够描述绝大多数情况下频率稳定性的内在变化，但当采集数据包含多种非白的噪声时，方差并不收敛，因此产生了新的方法体系——Allan方差（Avar），其最初的主要用途是表征晶振的频率稳定度。后来，其用来评估和测量光纤陀螺的随机噪声特性［3-4］。但是，Avar以及其改进方案［5］只能对平稳信号进行分析，对实际的陀螺输出，由于长时间工作过程中会受到各项外界环境的影响，如温度、振动等干扰的影响，并不能保证陀螺仪输出信号的平稳性。

为此，本文采用了一种基于DAVAR的方法［6］来表征船用光学陀螺的动态随机误差特性。该方法能够完全兼容Avar，在保持其优势的基础上，能有效描述噪声在变化过程中的特性。顺利解决了Avar所面临的困难，能够有效地对随时间变化的各随机噪声项进行详细的量化。这对于实际应用中的船用光学陀螺仪的设计生产和实际使用具有重要意义。

1 陀螺随机噪声

光学陀螺在长时间使用过程中存在众多外界环境的干扰，如光强以及热效应等，均会导致其输出中会包含各种各样的随机噪声（误差）项。在对光学陀螺进行噪声特性分析时，很难建立噪声准确的物理-数学模型，而功率谱密度函数（Power Spectrum Density，PSD）可从另一方面定义噪声。这些噪声主要包括量化噪声（Quantization，Q）［7］、角度随机游走（Angle Random Walk，ARW）、零偏不稳定性（Bias Instability，BI）、速率随机游走（Rate Random Walk，RRW）、速率斜坡（Rate Ramp，RR）。另外，其还包括占比较小的正弦类型噪声和其他噪声项［8］，一般分析过程中可忽略。

Avar不仅可以从时域上描述信号的独特特征，而且在频域上，其与双边PSD之间存在一种特定的定量关系。因此，其不但可以定性地分析光学陀螺仪输出中的噪声类型，更能够准确量化各噪声的实际水平。两者之间的关系可表示为

式中：Sω(f)为随机过程的双边PSD。式（1）可以理解为将随机过程通过一个滤波器后，Avar与输出功率成正比，该滤波器的传递函数为sin4(πfτ)(πfτ)2，τ为相关时间，其决定了滤波器的带通，可以调节τ用来对不同类型的随机过程进行检测。

首先，假设各噪声在统计学意义上互不相关，且主要分布于不同的频段上，按照两者之间的内在关系［9］，将Avar表示为

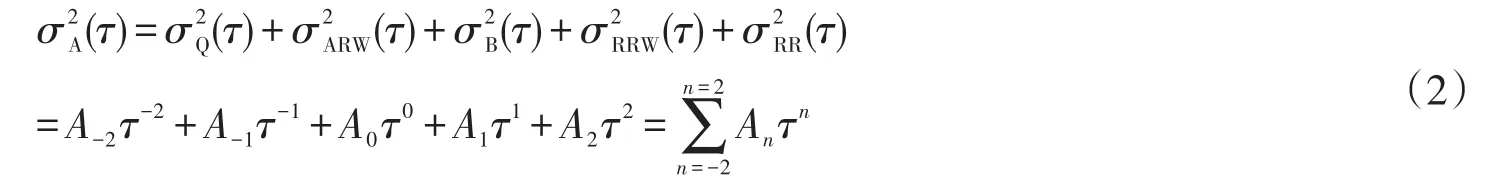
式中：An为所拟合的各项噪声的系数。一般采用双对数图（loglog）来表示τ和方差，最为典型的结果如图1所示。在整个相关时间上，不同的斜率的变化说明不同的噪声起主要作用。在图1中5种噪声所一一对应的斜率分别为-1～+1。

拟合随机噪声系数的方法分为：在线法［10］和后处理法，均通过最小二乘算法或者加权最小二乘法求取，如

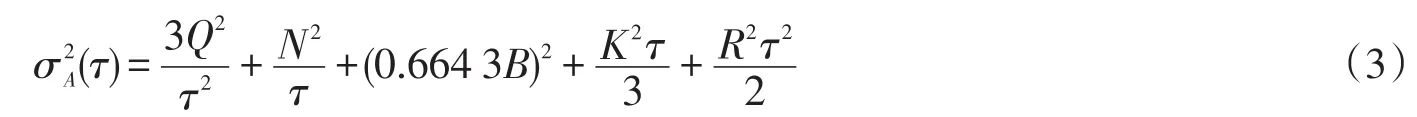
进而获得各噪声的拟合系数。表1为各噪声对应的τ值、单位和拟合参数的计算方法。

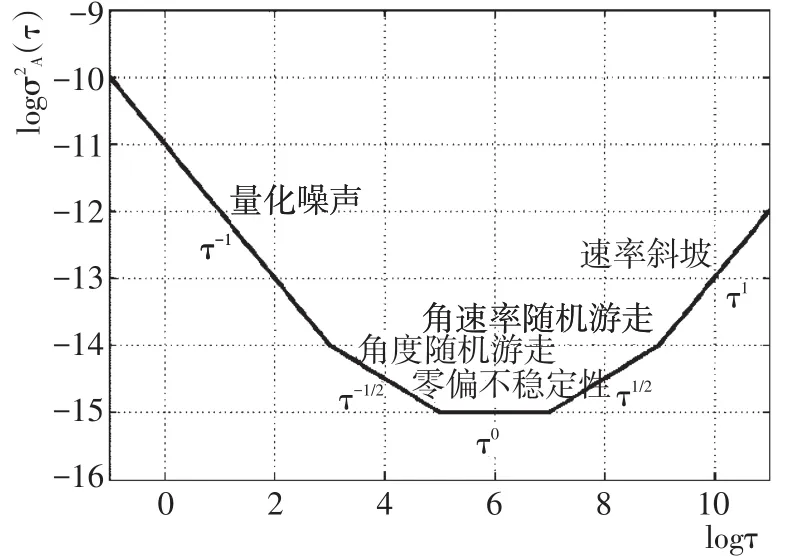
图1 τ与噪声的双对数图Fig.1 log-log plot ofτand noises

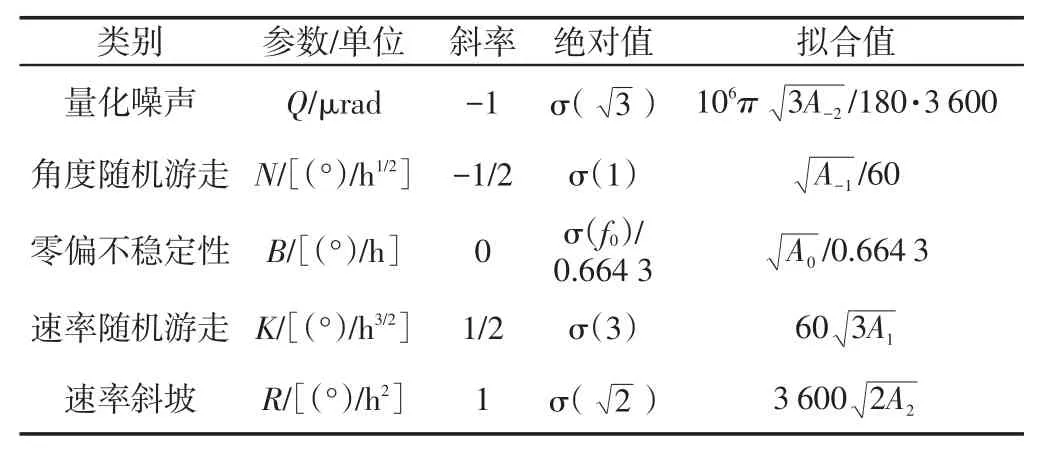
表1 最小二乘法得到的噪声系数Tab.1 Coefficient values obtained by LSM

2 Avar及其改进

1966年，David W Allan首次提出了Allan方差，其主要思想是利用差分，即数据的一次差分来研究晶振的频率稳定性。陀螺仪的输出和随机过程类似，因此完全可以采用Avar对陀螺仪输出数据进行分析，并对误差建模和滤波效果进行有效评价。

2.1 Avar的定义

利用给定的采样周期τ0，首先对原始输出信号进行采样，得样本{ωi,i=1,2,…,Nω}；然后，进行簇采样或抽样，即以τ=mτ0,m=1,2,…,Nω2为数据间隔进行分组，最大组数K=Nωm（整数）。因此，对于每一组m个数的数组，可计算其均值为

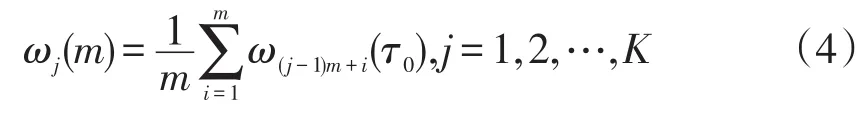
从时域上，可以将Avar定义为

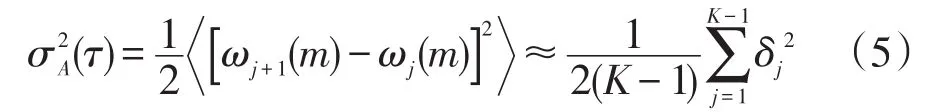
式中：δj=ωj+1(m)-ωj(m)为相邻两个数组均值之差；表示总体的均值，通过改变τ的值，即可得到对应的Avar。为了方便起见，采用其估计值形式，即

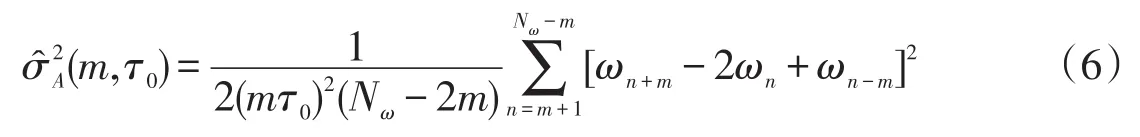
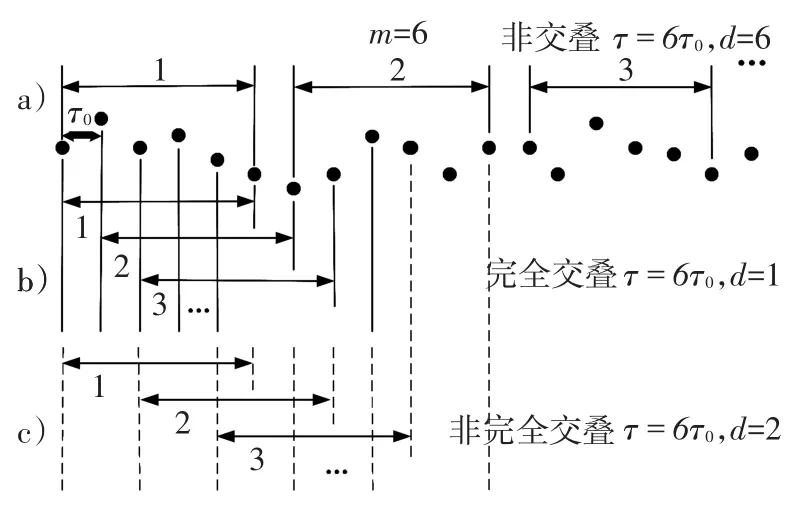
图2 3种不同的簇采样过程Fig.2 Three kinds of different cluster sampling process

2.2 Avar的改进

经典的Avar和2种改进后的Avar［11］的簇采样（抽样）过程如图2所示。

（1）统一形式。

2.1节所描述的Avar的采样方式完全适用于光学陀螺仪角速率输出数据的分析，即以dτ0为采样间隔进行采样，得到样本ω后，分别进行簇采样和均值求取，即得到

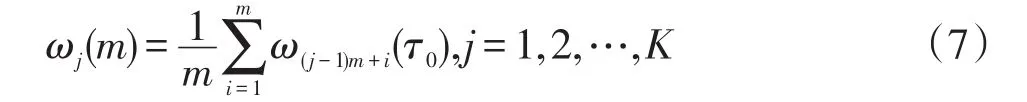
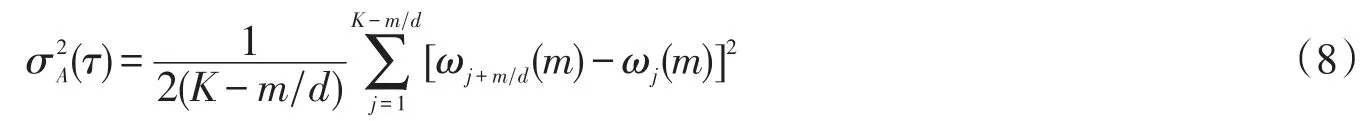
式中：若d=m，则K=Nωm。此时其退化为形如式（5）的经典Avar形式，其簇采样过程如图2（b）所描述，也称其为非交叠的Avar。

然而在时域内进行频率稳定性分析时，面临着如何将平均时间最大化以减小实际测量的时间消耗代价，并提高置信度，这是共性问题。换而言之，在确定的时间间隔内进行有效的数据采集，如何最大限度地发挥处所采集数据的作用是亟需解决的问题。传统的Avar随着分组数的减小，方差估计的置信度越来越差，因此，在实际中通常会采用不同的簇采样方法对结果进行修正。

（2）完全交叠的Avar。

若d=1，则K=Nω-m+1。相应地有

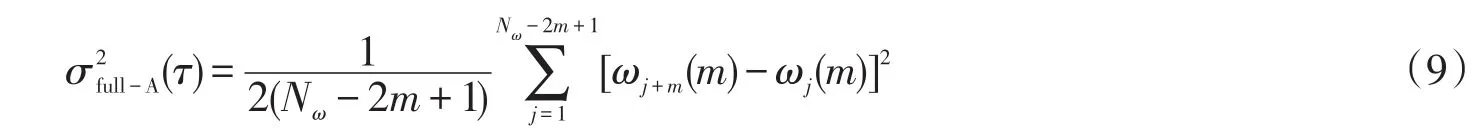
式中：σ2full-A(τ)为完全交叠的Avar，图2（b）所示为其实际的采样过程。显然，其性能优于经典的Avar，实现也最简单，计算代价也最小，因此得到了最为广泛的应用。

（3）非完全交叠的Avar。

若1＜d＜m，且m为d的整数倍，则式（8）为非完全交叠的Avar，图2（c）所示为其采样过程。图中m=6，d=2。

在进行频率稳定度估计时，估计值的置信度是必须给出的。由于Avar的估计值是基于有限长度数据的，因此对于有效组数为K的信号，置信度随着K的增加而提高。同时，对于Avar，估计的百分比误差为

采用修正后的Avar能够有效地提高置信度，且在置信区间计算时，采用χ2（卡方）分布函数。

3 动态Allan方差（DAVAR）

DAVAR的核心思想是：利用窗函数选择不同时间段内的时域数据，然后分别计算Avar，并将结果以三维形式给出。因此，DAVAR不仅兼容了Avar信息，同时还融合了时间信息。假设信号x(t)具有时变的性质，利用DAVAR分析该信号时，即可突破Avar只对于总体时间上的结果进行表征的限制，得到该统计特性随着时间的变化而改变的趋势。

DAVAR的计算过程，可按步骤分为：

（1）首先，选定第一个时间分析点t=t1；

（2）以L为长度，中心点为t1的窗口对信号ω进行有效截断；

（3）按照Avar的计算方法，对截断后得到的Nω个样本数据求取(t1,τ)；

（4）选择第二个时间分析点，如t=t2（t2的选择应使所截断的数据与t1点的截断数据产生一定的交叠），然后不断重复步骤（2）和（3），直至待分析的数据完全结束。

至此，若采用离散形式表达，DAVAR可表示为

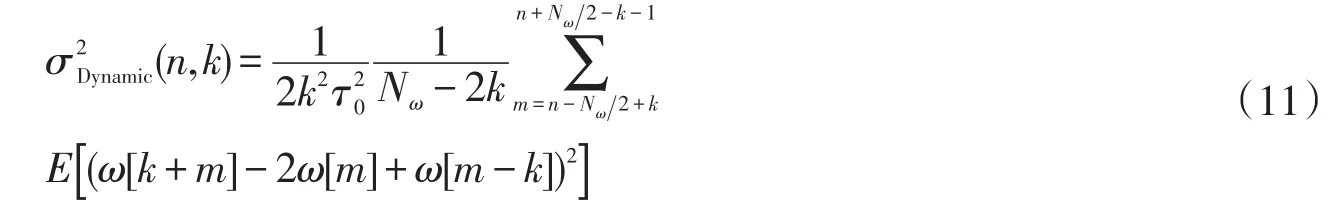
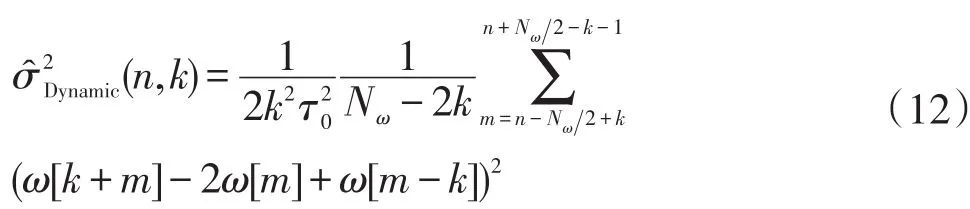
DAVAR方法比Avar能更全面地描述和量化光学陀螺的动态随机误差特性，尤其是在评价高精度陀螺的场合，其更有效。

可以看到，窗函数是实现Avar向DAVAR的过渡过程中的关键因素。事实上，各种窗函数在不同频段上性能也存在差异，例如，矩形窗对中低频的噪声分析能够满足其频率分辨率较高的独特要求；但是，Hanning窗能够对高频段的噪声有着较高精度的估计。由于单一的窗函数一般意义上无法完全保证所有类型的噪声辨识精度，因此在实际的应用过程中，采用哪一种或者是哪几种窗函数还需要进一步的理论分析和实验验证。

4 实验结果及讨论

分别通过仿真和光纤陀螺实际数据验证新方法的优越性。

（1）仿真验证。通过改变白噪声的方差或标准差，得到方差时变的噪声，然后在整个数据段上计算并比较Avar和DAVAR的结果。这里值得注意的是：选择DAVAR的窗函数时，选择宽度为201的矩形窗（窗函数宽度选择为奇数，以便数据进行拓展），分析时间段间隔数选定为20，之所以选择矩形窗是因为，根据先验知识可以了解到对于低频的噪声信息更需关注。结果如图3～图5所示。

从图3、图5中可见，在分析方差时变噪声时，Avar仅能够表征真各数据段上所有时域数据的结果；而DAVAR却能在整个时域上识别出各噪声的变化情况。实际上，在载体动态不大的情况下，即陀螺仪输出的噪声变化情况较小时，两者的效果相当，即DAVAR其优越性无法完全体现；但当动态变化较大时，Avar无法表征噪声的各种变化情况，此时DAVAR将完全展示其优越性。

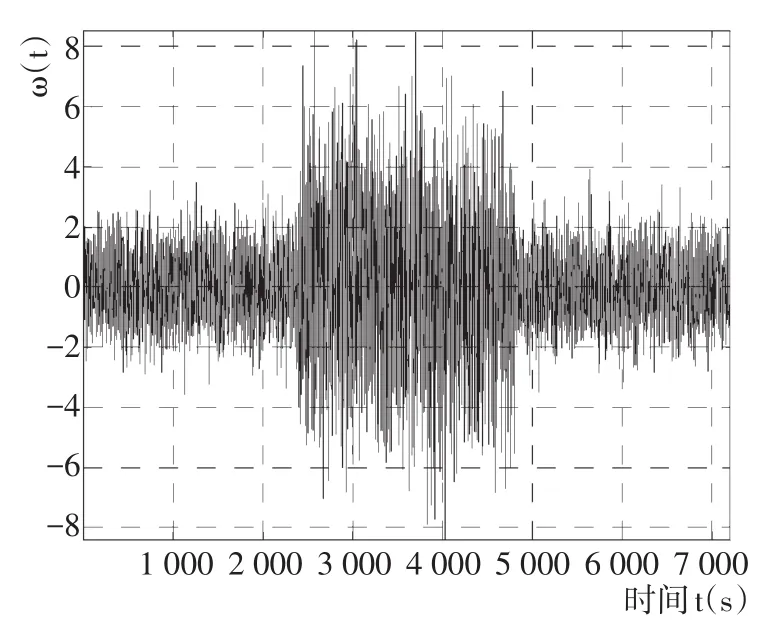
图3 方差时变噪声Fig.3 Noise with the time⁃varying variance

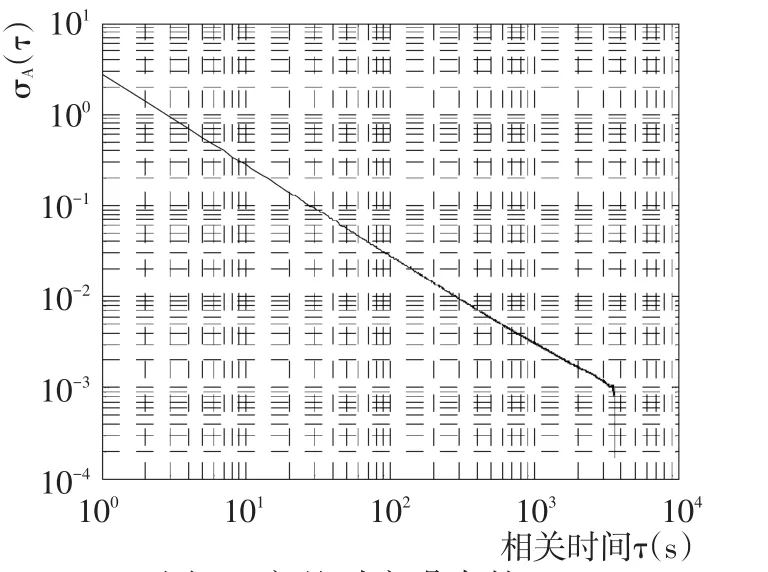
图4 方差时变噪声的AvarFig.4 Avar of noise with time⁃varying variance

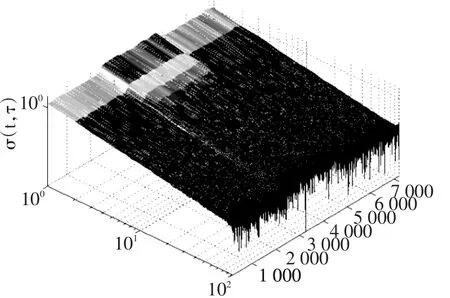
图5 方差时变噪声的DAVAR方差Fig.5 DAVAR result of noise with time⁃varying variance

（2）光学陀螺数据验证。

以光纤陀螺输出数据为例进行验证。分别利用2种方法辨识出光纤陀螺的误差类型，并计算得到相应的随机噪声参数，图6为光纤陀螺的实测输出和Avar。表2为所得到的各噪声拟合系数。

利用DAVAR对光纤陀螺输出数据的分析结果如图7所示，同样地以双对数结果呈显示。可见，陀螺所处的动态依旧较小，噪声变化也保持在较小的状态，但依然可清晰地看出方差在时域上的变化情况，而Avar是完全无法表征这部分变化情况的，其只能给出各噪声系数在所有时域数据上的统计的值。最后，通过分析可知该型号的陀螺仪的输出误差主要表现为量化噪声、速率斜坡和角度随机游走项，因此在实际的设计生产和使用过程中如果采用适当的手段降低这些噪声的影响，能够为提高陀螺仪精度提供重要指导。

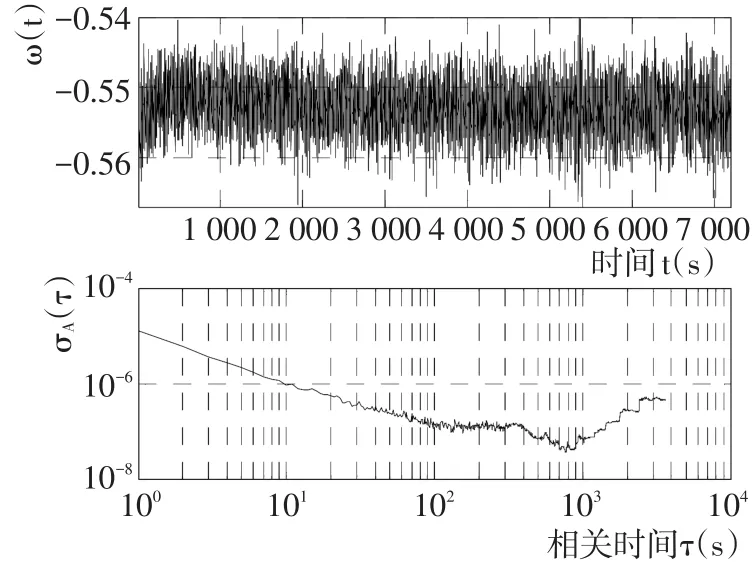
图6 光纤陀螺输出信号Fig.6 Output signal of the FOG

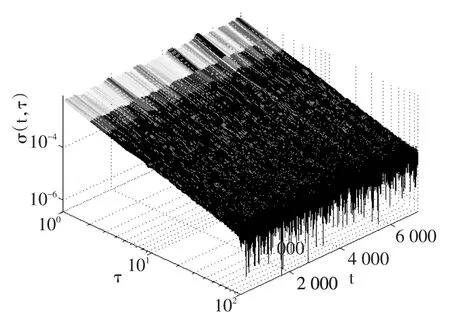
图7 光纤陀螺输出的DAVAR（双对数）Fig.7 DAVAR result of FOG′s output（loglog）

表2 各种类型噪声系数Tab.2 Noise coefficients of the FOG

5 结论

对于船用高精度的INS，光学陀螺的随机误差严重影响着该系统精度的提升。而经典的Avar并不能完全处理和分析陀螺仪随机误差动态过程，因而，本文采用DAVAR方法来分析光学陀螺动态过程中的光学陀螺仪输出的随机噪声。实验结果表明，DAVAR方法能够有效处理Avar不能够解决的噪声动态变化的问题缺陷，其不仅能够从时域上准确地识别出随机噪声的类型，并量化各噪声的实际水平，且同样能够对陀螺仪进行动态评估、对随机建模仿真和滤波效果进行一定的评价。这对于船用导航系统中陀螺仪的设计生产和性能评价具有重要的指导意义。

［1］査峰，高敬东，许江宁，等.光学陀螺捷联惯导系统发展与展望［J］.激光与光电子学进展，2011，7（1）：172-177. ZHA F，GAO J D，XU J N，et al.Overview on strapdown Inertial System consisted by Optical Gyros［J］.Laser&Optoelectronics Process，2011，7（1）：172-177.

［2］白俊卿，张科，卫育新.光纤陀螺随机漂移建模与分析［J］.中国惯性技术学报，2012，20（5）：621-264. BAI J Q，ZHANG K，WEI Y X.Modeling and analysis of Fiber Optic Gyroscope random drifts［J］.Journal of Chinese Inertial Technology，2012，20（5）：621-264.

［3］IEEE STD.IEEE standard specification format guide and test procedure for single⁃axis interferometric fiber optic gyros［R］.New York：The Institute of Electrical and Electronics Engineers，1998.

［4］Richard J V，Ahmed S Z.Statistical modeling of rate Gyros［J］.IEEE Transactions on Instrumentation and Measurement，2012，61（3）：673-684.

［5］汤霞清，程旭维，高军强.光学陀螺随机误差特性的混合理论方差方法分析［J］.兵工学报，2015，36（9）：1 688-1 695. TANG X Q，CHENG X W，GAO J Q.Hybrid theoretical variance analysis for random error properties of Optic Gyroscope［J］.Ac⁃taArmamentarii，2015，36（9）：1 688-1 695.

［6］Lorenzo G，Patrizia T.The dynamic Allan variance［J］.IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Con⁃trol，2009，56（3）：450-464.

［7］Savage P G.Analytical modeling of sensor quantization in strapdown Inertial Navigation error equations［J］.Journal of Guidance，Control，and Dynamics，2002，25（5）：833-842.

［8］Han S L，Wang J L.Quantization and colored noises error modeling for Inertial sensors for GPS/INS integration［J］.IEEE SensorsJournal，2011，11（6）：1 493-1 503.

［9］El⁃Sheimy N，Hou H Y，Niu X J.Analysis and modeling of Inertial sensors using Allan variance［J］.IEEE Transactions on Instru⁃mentation and Measurement，2008，57（1）：140-149.

［10］Miao Z Y，Shen F，Xu D J，et al.Online estimation method of Allan variance coefficients for MEMS IMU［J］.Journal of Instru⁃ment，2014：09001.

［11］Li J T，Fang J C.Sliding average Allan variance for Inertial sensor stochastic error analysis［J］.IEEE Transactions on Instrumen⁃tation and Measurement，2013，62（12）：3 291-3 300.

Dynamic analysis of random error properties for marine optic gyroscope

WEI Jian⁃cang,GUO Yue⁃shan,LIU Dong⁃na
（Tianjin Deepfar Ocean Technology Co.,Ltd.,Tianjin 300457,China）

The inertial technology is the unique effective methods to autonomously acquire marine position and attitude information,while the Ring Laser(RL)and Fiber Optic Gyroscope(FOG)were the key components of inertial navigation,guidance,and dynamic precise measurement systems,as study of random errors analysis can im⁃prove the accuracy of Marine′s weapon significantly.The error properties of Optic Gyroscope(OG)and variance analysis methods have been introduced and reviewed in detail.For testing and analyzing the stochastic error proper⁃ties,and quantifying the noises amplitude under dynamic environment more effectively,Allan variance and dynam⁃ic Allan variance(DAVAR)strategy were adopted,respectively.Comparing with each other,identifying the noise types,and quantifying noise of white noises with time⁃varying variances and gyroscope′s real outputs,experimental results show that DAVAR can distinguish and quantify time⁃varying noises in long⁃term run,and reflect the gyro⁃scope dynamic more accurately.

inertial navigation system;optic gyroscope;random error properties;variance analysis;DAVAR

V 249.32+5

A

1005-8443（2016）06-0657-06

2016-04-28；

2016-05-12

魏建仓（1981-），男，河北省廊坊人，高级工程师，主要从事水下机器人动力结构研究工作。

Biography：WEI Jian⁃cang（1981-），male，senior engineer.