波流耦合作用下海洋柔性立管防弯器动力响应数值分析

揭晓侠，李家旺，朱克强

（宁波大学海运学院，宁波315211）

波流耦合作用下海洋柔性立管防弯器动力响应数值分析

揭晓侠，李家旺，朱克强

（宁波大学海运学院，宁波315211）

基于三维动态时域分析软件OrcaFlex建立防弯器与立管耦合响应模型，对柔性立管防弯器在波流耦合作用下的动力响应进行了参数敏感性分析，结合分析结果对柔性立管防弯器系统进行优化布局，并分析了流向变化和浪向变化对弯矩的影响。结果表明，靠近立管与浮体或水下设备固结点的曲率和弯矩大，随着远离固结点，曲率和弯矩呈递减趋势。海流方向变化对立管和防弯器曲率和弯矩的影响较浪向变化更大。底部立管和防弯器弯矩高于顶部，需格外注意。防弯器曲率与立管曲率基本一致，但弯矩高出很多，达到了防弯器保护立管承载过度屈曲的目的。

柔性立管；防弯器；OrcaFlex；波流耦合作用；动力响应；曲率；弯矩

随着陆地资源的枯竭，人类逐渐向海洋进军获取能源，为了获取海洋尤其深海蕴藏的丰富油气资源，海上油气开采装备取得了较大的发展。其中针对深水环境中，浮式生产系统（Floating Production Storage and Offloading）应用最为广泛。该系统通常的做法是通过海洋柔性立管把上端的浮式生产设施与下端的海底设备相连进而实现油气的开采控制。考虑到立管与浮体及海底连接处都是刚性连接，而立管在海水中受到流的作用会不断扭动，所以连接点会受到较大的弯矩，弯矩如果超出立管的屈曲强度，立管就失效了。所以需要在连接点处加上附件即防弯器（bending stiffener）进行保护。典型的防弯器如图1所示，其主体部分呈圆锥状。

图1 防弯器简图和实物Fig.1 Bend stiffener diagram and entity

防弯器是套在管或缆上的一个由聚合物材料制造的锥形构件，具有良好的弹性和变形能力，在海洋工程中作为防止柔性管线过度弯曲的主要保护构件［1］。弯曲限制器由于占用空间小、安装方便并且对管或缆的保护效果好，在海洋工程中得到快速发展和广泛使用。

孙凯等［1］建立了海洋柔性立管防弯器三维有限元模型，研究材料非线性对防弯器性能的影响。孙崎等［2］采用进化策略的优化方法对防弯器的结构进行优化设计，并与不同优化方法的计算结果进行对比，表明该方法优化效果明显。席勇辉等［3］采用梁单元建立防弯器等效平面模型并进行数值分析，给出防弯器和管缆在位分析的高效计算方法。Droby⁃shevski［4］研究了弹性杆非线性弯曲的特性，并给出理论分析方法进行防弯器的设计，最后通过实际例子证实了该理论的可行性。Bazan［5］等使用细长梁程序和进化策略的多目标算法，给出防弯器的最优设计方法，该方法结果与有限元法类似，但计算量明显减少，数值例子则表明了该方法的有效性和鲁棒性。Zhang［6］等对柔性立管的弯曲特性进行了理论和数值研究，通过与相关实验数据的对比，验证了研究有效性。

国内外关于防弯器的研究大多数集中在防弯器的结构优化，对于防弯器和立管整体受到水上浮体和波浪以及海流的作用而产生的力学响应研究比较少。本文基于大型水动力学软件OrcaFlex上建立防弯器与柔性立管的耦合响应的模型，通过加载浪和流等外部环境载荷，实现了全时域仿真计算分析。

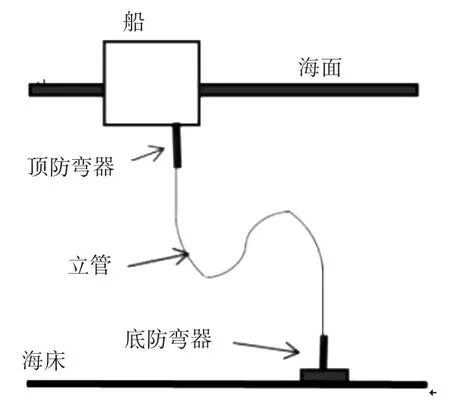
图2 防弯器模型Fig.2 Bend stiffener model

1 理论基础

OrcaFlex软件利用扩展的莫里森方程来计算管道、缆绳和浮体的水动力载荷。莫里森方程最初是莫里森和同事在20世纪50年代针对竖直圆柱体计算波浪载荷时提出的，莫里森方程假设结构物的存在不影响波浪特性。波浪载荷可以描述为波浪流体加速度产生的惯性力和粘性产生的摩擦力之和。运动的结构物也可以使用莫里森方程计算载荷，需要考虑相对速度。

扩展的莫里森方程如下

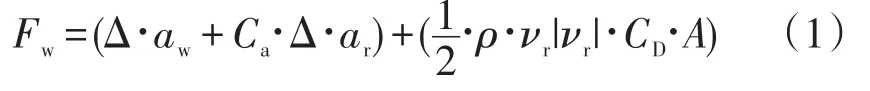
式中：Fw为波浪载荷；Δ为结构物的排水质量；aw为水质点相对于地球的加速度；Ca为结构物的附加质量系数；aw为水质点相对于结构物的加速度；ρ为水的密度；νr为水质点相对于结构物的速度；CD为结构物的拖曳力系数；A为拖曳力面积。

公式中第一个括号表示惯性力，第二个括号是拖曳力。惯性力由两部分组成，第一部分与水质点相对于地球的加速度成正比，另一部分与水质点相对于结构物的加速度成正比，即附加质量力。

2 计算模型

图2所示为柔性立管陡峭型波浪布置，立管拱起区段由连续浮子提供浮力，在OrcaFlex中用

“Line with Floats”模式来建立浮子模型。为简便计，海床模型采用线性海床模型。浮体采用船模型，船舶方向为90°，因此正视图中呈现的是船舶的横截面。与海床连接的是管汇，在立管与船舶和管汇固结点处加装防弯器。

系统各部分结构对应的参数如下，防弯器主要参数如表1所示，水面上浮体为船，其主要参数如表2所示，柔性立管基本参数如表3所示。

表1 防弯器主要参数Tab.1 Major parameter of bend stiffener

表2 浮体主要参数Tab.2 Major parameter of ship

表3 立管主要参数Tab.3 Major parameter of riser

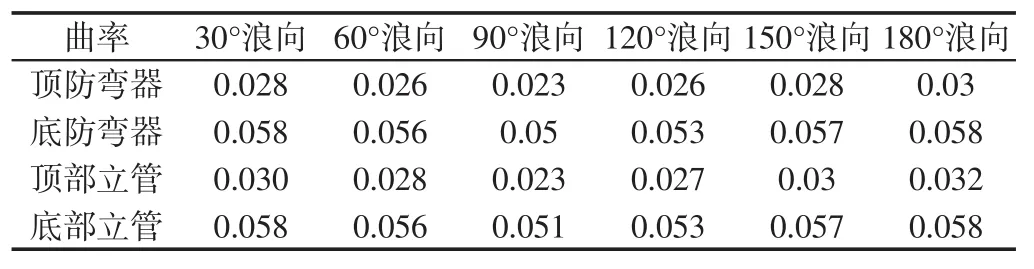
表4 不同浪向下立管和防弯器曲率Tab.4 Curvature of bend stiffener and riser under different wave directions rad/m

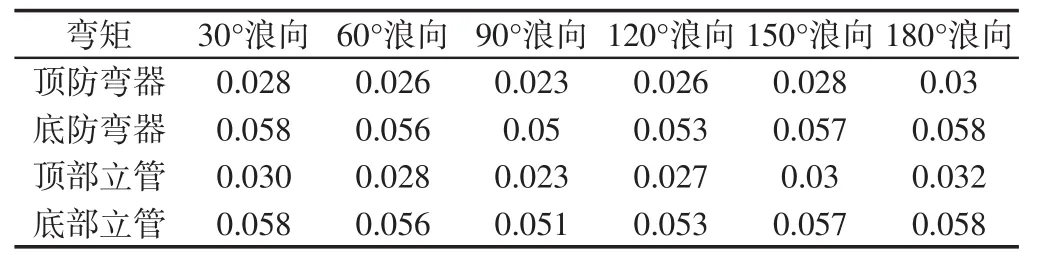
表5 不同浪向下立管防弯器弯矩Tab.5 Bend moment of riser and bend stiffener under different wave directions kN·m

3 算例分析

立管防弯器系统在水中会受到波浪和水流的耦合作用。方位不同的浪向对船舶的作用存在差异，因而会对与船舶固结立管造成不同程度影响。海流的方位对立管的响应也存在影响。以下将根据具体算例对其进行研究。

3.1 浪向变化的影响

为了寻求最优化系统布局，通过变化浪向，得到各部分在不同的浪向条件下的最大曲率和最大弯矩，如表4、表5所示。采用控制变量法［7］，参考南海某海域夏季水文环境，由于该海域波浪随季节呈现一定的统计规律，为简便计，取波高2 m，周期16 s，得到上防弯器、下防弯器和立管的最大曲率和最大弯矩。

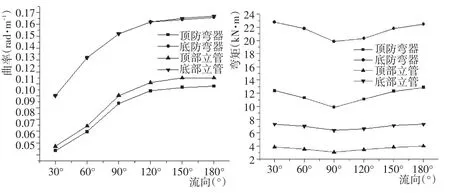
图3 不同浪向下立管和防弯器曲率弯矩变化Fig.3 Variation of curvature and bend moment of riser and bend stiffener under different wave directions

根据表4和表5得出图3，该图清楚地表明立管和防弯器最大曲率和最大弯矩随着浪向的变化而变化。

由图3可知：顶端及底部防弯器和其所包裹的立管的曲率基本一致，而底部曲率高于顶部曲率。顶部和底部防弯器弯矩均高出立管弯矩很多，底部立管和防弯器弯矩均大于顶部。曲率和弯矩均出现先减小后增加的变化趋势，在波浪方向为90°时候达到最小。根据计算，波浪方向的改变对顶部防弯器、底部防弯器、顶部立管和底部立管曲率的最大影响分别达到21.7%、16%、25.2%、17.6%；对顶部防弯器、底部防弯器、顶部立管和底部立管弯矩的最大影响分别达到25.3%、14.7%、 25.2%、14.7%。

3.2 流向变化的影响

参考南海某海域夏季水文环境，取流速为1.5 m/s。改变流向，得到上防弯器、下防弯器和立管的最大曲率和最大弯矩，如表6、表7所示。

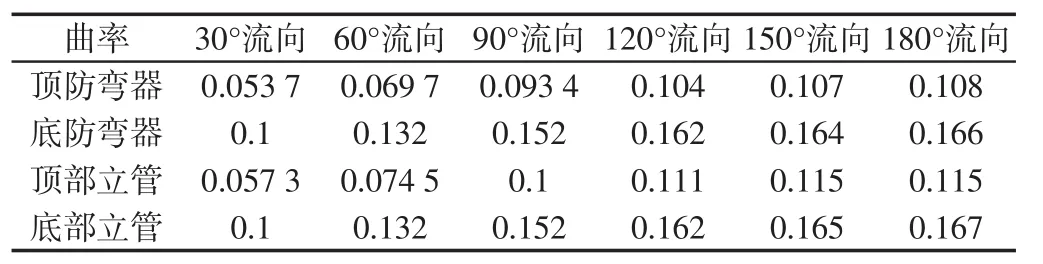
表6 不同流向下立管和防弯器曲率Tab.6 Curvature of riser and bend stiffener under different current directions rad/m

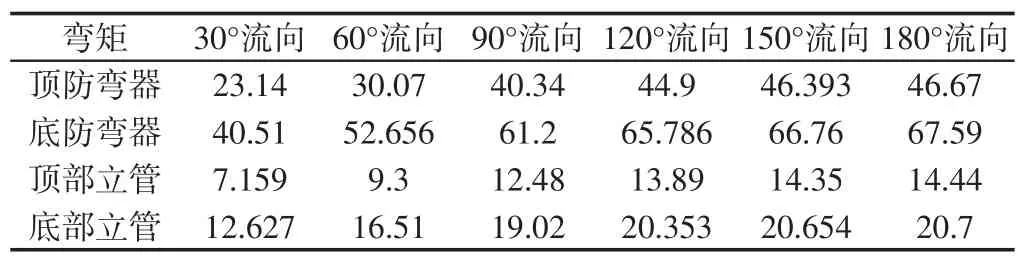
表7 不同流向下立管和防弯器弯矩Tab.7 Bend moment of riser and bend stiffener under different current directions kN·m

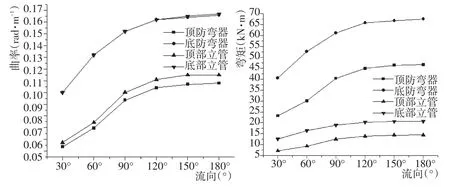
图4 不同流向下立管和防弯器曲率弯矩变化Fig.4 Variation of curvature and bend moment of riser and bend stiffener under different current directions

表8 不同浪向流向立管和防弯器曲率Tab.8 Curvature of riser and bend stiffener under different wave directions rad/s

根据表6和表7得出图4，图4清楚地表明立管和防弯器最大曲率和最大弯矩随着流向的变化而变化。

由此可知，立管和防弯器的曲率和弯矩都随着海流方向单调递增。顶部和底部立管和防弯器的曲率大致相等，而底部曲率高于顶部曲率。防弯器弯矩高出立管弯矩很多。在海流方向到达180°时，曲率和弯矩均同时达到最大。据计算，海流方向的改变对顶部防弯器、底部防弯器、顶部立管和底部立管曲率的最大影响分别达到101%、66%、100%、67%；对顶部防弯器、底部防弯器、顶部立管和底部立管弯矩的最大影响分别达到101.7%、66.8%、101.7%、63.9%。

3.3 波流耦合作用的影响

为了分析波流耦合作用，分别取浪向180°，流向180°；浪向90°，流向30°。各部分最大曲率和最大弯矩如表8、表9所示。

由表可知，浪向180°、流向180°比浪向90°、流向30°的顶部防弯器、底部防弯器、顶部立管、底部立管的最大曲率分别高出68.4%、102%、68.3%、106%。最大弯矩则分别高出68.4%、114%、68.2%、106%。

表9 不同浪向流向立管和防弯器弯矩Tab.9 Bend moment of riser and bend stiffener under different current directions kN·m

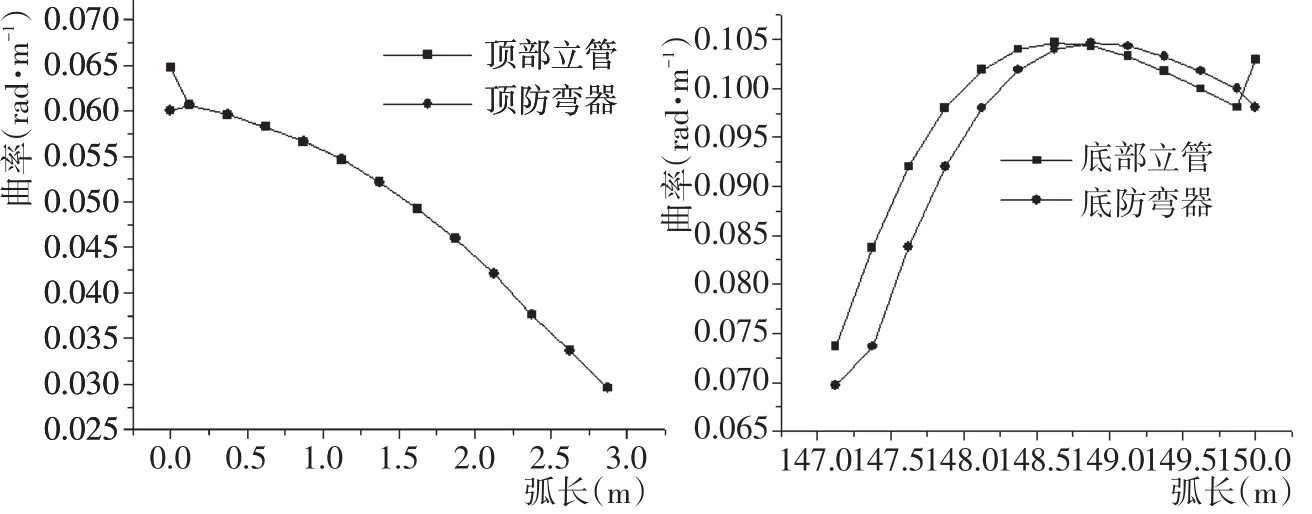
图5 立管和防弯器曲率随弧长变化Fig.5 Curvature variation of riser and bend stiffener along arc length

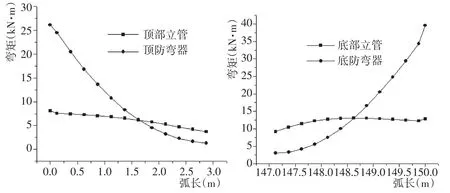
图6 立管和防弯器弯矩随弧长变化Fig.6 Bend moment variation of riser and bend stiffener along arc length

设定浪向90°，流向30°，得到立管和防弯器上曲率和弯矩随弧长的变化曲线，如图5、图6所示。

由图可知，在顶部立管和防弯器，越靠近立管与浮体固结点的曲率越大。对于底部立管和防弯器，越靠近立管与海底设备固结点曲率越大。曲率越大，则弯矩越大，可以从图6得到验证。

4 结论

本研究基于OrcaFlex建立了柔性立管与防弯器的动力耦合响应模型，对模型在不同的环境载荷作用下的动力响应进行了参数敏感性分析，主要分析结论如下：

（1）防弯器和立管曲率基本保持一致，且底部数值高于顶部数值。防弯器弯矩高出立管很多，达到防弯器减小立管弯矩的目的。

（2）靠近立管与浮体或水下设备固结点的曲率和弯矩大，随着远离固结点，曲率和弯矩呈递减趋势。通过波流耦合作用下全时域仿真，浪向90°，流向30°，立管和防弯器曲率和弯矩最小。

（3）立管和防弯器曲率和弯矩随着浪向递增而呈先递减后递增的变化趋势，随着流向单调递增变化。海流方向变化对立管和防弯器曲率和弯矩的影响较浪向更大。浪向180°，流向180°比浪向90°，流向30°的顶部防弯器、底部防弯器、顶部立管、底部立管的最大曲率分别高出68.4%、102%、68.3%、106%。最大弯矩则分别高出68.4%、114%、68.2%、106%。

［1］孙凯，岳前进，阎军，等.基于材料非线性的海洋柔性立管防弯器有限元分析［J］.计算机辅助工程，2014（6）：66-69. SUN K，YUE Q J，YAN J，et al.Finite element analysis on bending stiffener of flexible marine riser based on material non⁃lineari⁃ty［J］.Computer Aided Engineering，2014（6）：66-69.

［2］张崎，姬鸾，黄一，等.基于进化策略的柔性立管防弯器优化设计［J］.华中科技大学学报：自然科学版，2014（6）：48-51.ZHANG Q，JI L，HUANG Y，et al.Optimization design of bend stiffener based on evolution strategy principle［J］.Huazhong Univ.of Sci.&Tech.：Natural Science Edition，2014（6）：48-51.

［3］席勇辉，阎军，杨志勋，等.基于异形梁模型的海洋柔性管缆防弯器数值模拟［J］.计算机辅助工程，2014（3）：60-64. XI Y H，YAN J，YANG Z X，et al.Numerical simulation on bending stiffener of flexible marine pipe/cable based on special beam model［J］.Computer Aided Engineering，2014（3）：60-64.

［4］Drobyshevski Y.Investigation into non⁃linear bending of elastic bars with application to design of bend stiffeners［J］.Marine Struc⁃tures，2013（31）：102-130.

［5］Bazán F A V，Lima E C P D，Siqueira M Q D，et al.A methodology for structural analysis and optimization of riser connection joints［J］.Applied Ocean Research，2011，33（4）：344-365.

［6］Zhang M，Chen X，Fu S，et al.Theoretical and numerical analysis of bending behavior of unbonded flexible risers［J］.Marine Structures，2015，44：311-325.

［7］梁辉，林影炼，方伟，等.水下脐带缆终端安装多浮体运动响应的数值模拟［J］.机械与电子，2015（10）：17-19. LIANG H，LIN Y L，FANG W，et al.Multi⁃body Response Analysis of Subsea Umbilical Termination Assembly Installation［J］. Machinery&Electronics，2015（10）：17-19.

Mathematical analysis for dynamic response of bending stiffener of ocean flexible subjected to coupled effects of waves and currents

JIE Xiao⁃xia,LI Jia⁃wang,ZHU Ke⁃qiang
（Faculty of Maritime and Transportation,Ningbo University,Ningbo 315211,China）

In this paper,the model of response of bending stiffener coupled with riser was built based on Or⁃caFlex,a three⁃dimensional dynamic time domain analysis software.Considering the coupled response of waves and currents,parameter sensitive analysis was made for dynamic response of the system of riser and bend stiffener.Be⁃sides,based on the above analysis results,layout of the system of the riser and bend stiffener was optimized,and the effect of the variety of wave direction and current direction on bend moment was analyzed.Simulation results indi⁃cate that the curvature and bend moment are larger on section closed to joints than on others,and will decrease along the direction which is apart from joints.The effect of the variety of current direction on curvature and bend moment of riser and bending stiffener is larger than that of wave direction.Curvature and bend moment downside is larger than that of upside.Bend stiffener is almost the same with riser on curvature,but larger on bend moment, which achieves the goal of protecting riser from excessive bending for load bearing.

flexible riser;bending stiffener;OrcaFlex;the coupled effect of waves and currents;dynamic re⁃sponse;curvature;bend moment

P 731.2;O 242.1

A

1005-8443（2016）06-0630-05

2016-04-04；

2016-05-03

国家自然科学基金资助项目（11272160）；国家自然科学基金青年项目（51309133）

揭晓侠（1990-），男，江西省玉山人，硕士研究生，主要从事海洋工程挠性管线结构动态响应研究。

Biography：JIE Xiao⁃xia（1990-），male，master student.