电推进系统Xe物理特性计算方法

陈涛,刘国西,宋飞,武葱茏

北京控制工程研究所,北京100190

电推进系统Xe物理特性计算方法

陈涛＊,刘国西,宋飞,武葱茏

北京控制工程研究所,北京100190

空间电推进系统的工质为Xe,其工作温度范围为-30～45℃,该范围覆盖Xe的临界点。在临界点附近,Xe可能呈现出多种形态,且对温度和压力变化十分敏感,采用传统状态方程在上述范围内计算其物理参数偏差最大可达30%。为解决这一问题,以CH4作为参考流体,建立了一种基于对比态原理的Xe物理特性计算方法。该方法能够对包括气相、液相、超临界区域的所有状态Xe物理性质进行准确计算。试验研究与国外数据对比的结果表明,在整个压力-温度范围内,计算误差小于0.5%。

电推进;Xe;超临界;对比态原理;物理特性;状态方程

电推进技术是一种利用电能加速推进工质,从而实现高比冲的先进航天器推进技术,由于其高比冲的优势,在先进国家的大型卫星平台及微小卫星平台上得到日渐广泛的应用[1-8]。

Xe作为电推进系统的工质,具有分子量大、熔点高、沸点高及临界点高等特点。考虑到系统的稳态工作、充气加压等过程,其工作温度范围为-30～45℃,压力范围为1～30 MPa。整个工作范围覆盖氙的临界点。在临界点附近,Xe状态对温度和压力变化十分敏感,分子间的作用力不可忽略,表现出强烈的真实流体特性。除此之外,在上述范围内,Xe可能呈现出液态、气态、气液混合态以及超临界态等多种形态。

目前,比较常用的描述真实流体性质的状态方程可以分为两大类:解析形式和非解析形式。解析形式的状态方程主要特点是当温度T、压强p给定时,体积V可以解析地求出,即方程中V的次数不超过4次,例如Redlich-Kwong方程[9]、Peng-Robinson方程[10]、Soave-Redlich-Kwong(SRK)方程[9]等;非解析形式的状态方程由于V次数较高,只能采用数值方法进行求解,例如Benedict-Webb-Rubin(BWR)/Modified Benedict-Webb-Rubin(MBWR)方程、Wagner方程等。

通过比较发现,以上几种传统状态方程无法同时准确计算各种形态下氙单质的p-V-T关系,计算偏差最大可达30%,精度无法满足应用需求。而精确获得上述关系对于Xe的充气加压、发射场加注及在轨监测都极为重要[11-12]。

因此,深入了解Xe物理特性,对电推进系统设计具有重要意义[13]。目前,国内外没有公开发表的计算方法。为了解决这一问题,本文主要针对电推进系统工质Xe的物理特性开展理论分析及计算方法研究。

1 理论模型及计算方法

典型物质的三维热力学曲面如图1所示[9]。按照流体所处的不同状态可以分为固相、液相、气相三种不同相存在。在工程应用中,常常需要对不同状态下物质的物理特性进行计算。

在大量的实际应用中,研究人员提出了各种各样的状态方程来描述p-V-T之间的关系。状态方程中最简单、最常见的是理想气体状态方程,主要适用于气体密度较低(即压力不太高、温度不太低)分子间相互作用可以忽略不计的情形。当压力较高或温度接近饱和气体温度时,分子间的作用力不可忽略,为了能描述真实工质的热物理属性,必须采用在低温和高压下都能对真实流体性质进行刻画的状态方程。

由于传统真实流体模型在高压区、液态区和临界点附近计算结果偏差较大,本研究中采用对比态原理结合BWR方程[14]来计算Xe的p-V-T关系。

1.1 对比态原理

对比态原理(Corresponding State Principle, CSP)是指:对所有物质来说,其状态变量经过恰当的无量纲化处理后,都遵从普遍的变化规律。例如,对p、V、T都以临界点参数进行归一化处理后(即pr=p/pc,Tr=T/Tc,Vr= V/Vc),pr-Vr-Tr关系对于所有同类极性物质都一样。

对比态原理是目前应用最广泛的物性估算方法。也就是说,在获得参考流体的物性试验数据后,就可以采用对应的对比态理论来计算目标流体的物性。对于具有不同分子结构而显现出不同极性的流体,按照对比态理论中使用参数的个数,可以分为2参数CSP、3参数CSP和4参数CSP。不同的模型适用于不同的物质类型。

由于Xe属于单原子球形分子,本文选取同极性的具有球形分子结构的CH4作为参考流体,采用2参数对比态原理结合BWR方程来计算Xe的物理特性。

2参数CSP是指,仅用两个特征性质来使状态条件无量纲化(不需引入新的无量纲特征参数),其特征参数为Tc和pc或者Tc和Vc。只有单原子物质如Ar、Kr、Xe或简单流体才精确地遵循2参数对比态原理,其他物质都有一些偏离。

1.2 BWR状态方程

BWR方程[14]能同时对气相、液相区域的物性进行准确的估算。方程将温度多项式与密度的幂级数和指数相结合,其具体表达形式为

其中,15个系数An的具体形式如表1所示,除了参数r外,与温度有关的函数共涉及32个拟合参数。

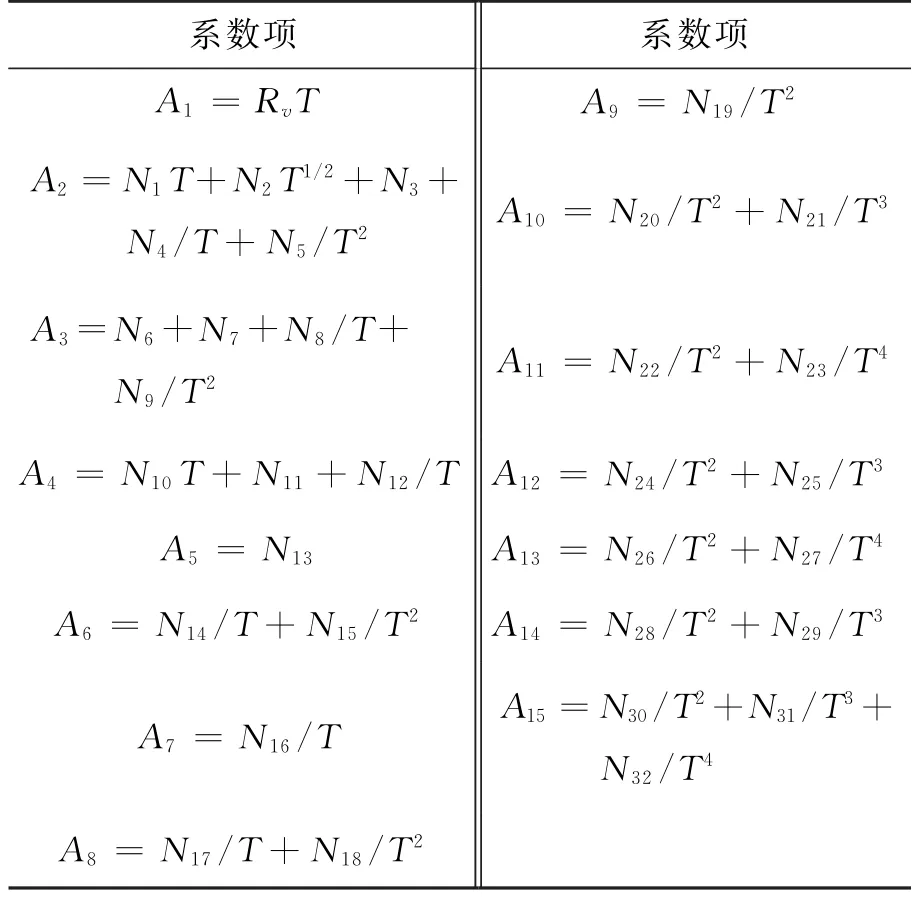
表1 BWR方程中系数项Table 1 Coefficient items in BWR equation

BWR方程中共有32个拟合参数,文献基于CH4大范围的试验数据给出了BWR模型中对应的32个参数取值,见表2。文献[15]指出,采用该组参数取值对CH4物性进行计算,最大误差不超过0.45%。

1.3 气液状态辨识方法

由于计算过程中涉及气、液、气液混合等多种状态,为了对流体状态进行辨识,本文基于美国国家标准技术研究院(NIST)数据库中CH4的饱和点数据,来获得CH4饱和状态下压力和温度的对应关系。拟合得到的气化线为

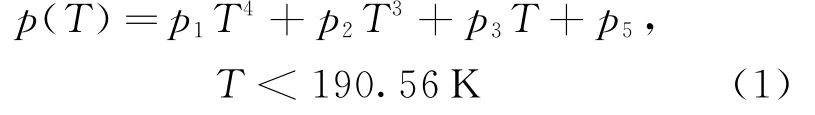
式中:p1=1.383×10-8,p2=-3.04×10-6,p3=0.0002654,p4=-0.01427,p5=0.4669。对于给定的温度,可以得到该点下的饱和蒸气压。若流体压力高于该数值,则流体处于液态,反之处于气态。

在此基础上,Xe的气液状态辨识通过式(1)结合对比态理论实现。

1.4 模型求解流程

采用对比态原理对Xe密度进行求解时,首先根据Xe的温度、压力参数,无量纲化处理后,采用对比态理论获得参考流体CH4对应的参数,在此基础上,反求BWR方程得到CH4的密度,再根据对比态理论求得Xe的状态参数。

2 试验系统及试验方案

为了对理论模型的正确性进行验证,同时获得Xe第一手试验数据,开展Xe物理特性试验研究。

2.1 系统组成

Xe物理特性试验设备组成及工作原理如图2所示,设备主要包括高纯置换气体、气体净化器、回收气瓶、Xe运输罐、称重装置、高低温箱、真空泵、高压气瓶、高精度测量与控制系统。其中高压气瓶是本试验中的主要试验装置,通过充入不同质量的Xe实现不同密度条件下的参数测量;高精度测量系统用于监测Xe运输罐质量,高低温箱中Xe的质量、记录压力容器内温度、压力变化数据采集频率不低于50 Hz;高低温箱用于控制试验中高压气瓶所需恒定温度,恒温精度不低于0.5℃。

试验介质选用高纯Xe,纯度≥99.995%。

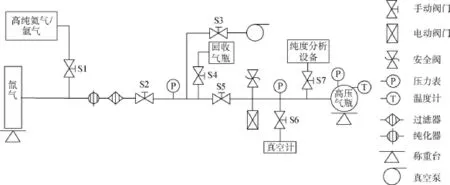
图2 Xe物理特性设备原理Fig.2 Schematic of the xenon physical property experiment equipment

2.2 试验方法

首先对高压气瓶容积进行标定。获得其精确容积之后,采用定容法测定Xe的p-V-T关系。在依次完成抽真空、置换、高纯置换之后,对高压气瓶吸入一定量的高纯度Xe,后启动高低温箱对高压气瓶进行升温、降温的过程,依次进行该密度下Xe压力随温度的变化规律测量;之后对高压气瓶再充入定量Xe,再重复上述降温回温过程,实现另一密度条件下的数据测量。以此类推,依次完成0.2 kg/L、0.4 kg/L、0.6 kg/L、0.8 kg/L、1.0 kg/L、1.2 kg/L、1.4 kg/L和1.6 kg/L密度条件下的数据测量。

3 计算结果及试验对比分析

根据BWR模型和对比态理论开展Xe物理特性计算,并与NIST数据[16]及试验结果进行对比以验证计算方法的正确性。

Xe的临界点参数如表3所示。当温度高于Tc时,Xe只处于气体状态。当温度压力都高于临界点参数时,此时称为超临界状态。这一状态下,流体的密度表现得像液态,但输运特性表现得像气态。

参考流体CH4的临界点参数见表3。

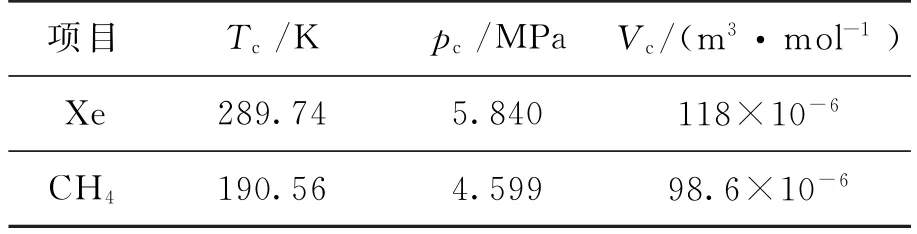
表3 Xe及参考流体CH4的临界点参数Table 3 Critical point parameters of Xe and CH4

3.1 饱和液线及饱和气线

当流体从液态变为气态时,会经历如下几个状态:液态、饱和液体态、气液混合态、饱和蒸气态和气态。采用对比态原理计算得到的Xe气化线如图3所示,计算温度范围为170～289.74 K,覆盖从三相点到临界点所有工况。可以看到Xe在饱和态或者气液混合态压力随温度的变化关系。对应的饱和气线和饱和液线分别如图4和图5所示。结果表明,采用本文提出的方法与NIST数据符合较好,饱和线上密度计算最大误差小于0.1%,能较好地分辨Xe给定压力和温度下的物理状态。

3.2 热力学曲线

为了验证程序在大范围内计算结果的有效性,对横跨液相、气液混合、气相区的温度和压力组合进行密度计算,来获得Xe的热力学曲线,并与NIST数据[16]进行对比。温度计算范围170～600 K,压力计算范围1～30 MPa,计算结果如图6所示。可以看到,计算结果与NIST数据完全吻合,能准确辨识流体状态。证明计算结果准确可信,可以用于给定温度T、压力p条件下电推进系统工质Xe的密度计算。

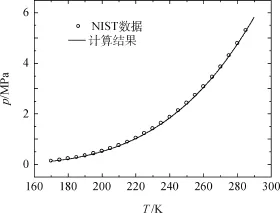
图3 Xe的气化线Fig.3 Evaporating line of xenon

图4 饱和液线Fig.4 Saturation liquid line of xenon

图5 饱和气线Fig.5 Saturation gas line of xenon

图6 1～30 MPa范围内Xe的T-ρ关系Fig.6T-ρrelationship in 1～30 MPa for Xe

对于工程应用中的典型密度值,将计算数据(ρth为理论计算结果)汇总,并与试验结果进行对比,如图7所示,平均误差小于0.5%。可以看出,各密度条件下,计算结果与试验数据符合良好,证明了计算方法可以完全满足电推进系统设计需求。

图7 计算数据与试验数据对比Fig.7 Comparison between calculation and the experiment

由图7中可以看到,在不同密度条件下,当温度逐步降低时,压力都呈下降趋势。同时,高压气瓶中Xe密度在临界密度(ρc=1.1029 kg/L)附近和远离临界点时,两者的变化趋势存在显著不同。例如,ρ=2.0 kg/L时,图7中p-T关系存在明显的转折点,真实流体的特性表现明显;而ρ=1.0 kg/L,压力随温度变化平缓,曲线较为光滑。

结合Xe三相图在密度压力平面的投影,即图8中的ρ-P图可以发现,在不同密度条件下,随着温度(或压力)的降低,Xe经历的相变并不相同。当密度大于临界密度1.102 9 kg/L时,Xe从40℃降低到-30℃过程中,会经历从超临界态变为液态,再到气液混合态的情形;而当密度小于1.102 9 kg/L时,会经历从超临界态变为气态,再到气液混合态的情形。这是图7中p-T关系在不同密度条件下变化趋势存在区别的原因。

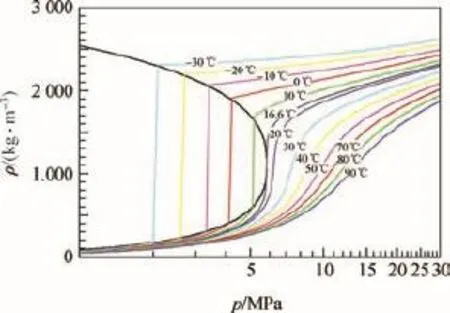
图8 Xeρ-p关系Fig.8 Relationship betweenρ-pfor Xe

4 结束语

本文对电推进系统工质Xe的物理特性进行了理论分析,建立了对应的真实流体状态方程,通过开展试验研究、并国外NIST数据库对比分析,结果表明:

1)建立的计算方法原理简单,计算方便,基于现有数据,无需提供额外参数。

2)在整个压力-温度范围内,该方法能够准确对气相、液相、超临界区域的Xe物理性质进行计算,误差小于0.5%,能够完全满足电推进贮供系统设计的应用需求。

3)研究过程中采用试验方法合理有效,能用于Xe高精度物性测量。

4)由于临界温度较高,在电推进系统的使用温度范围内,氙的真实流体的特性表现明显,在不同密度条件下,p-T关系存在典型的差异。

References)

[1] ZHANG T P,WANG L,WU X M.Electric propulsion development for DFH-4SP satellite platform[C]∥Proceedings of 65th IAC,Toronto,Canada,IAC-14-C4.4.2,2014.

[2] VALERIE C T,JOSEPH M M,GBROWN J M.The dawn spacecraft[J].Space Sci.Rev.,2011,163(1): 175-249.

[3] ADAM S,ALEC D G,PETER Y P.Performance of a helicon Hall thruster operating with xenon,argon and nitrogen[J].Journal of Propulsion and Power, 2014,30(3):664-671.

[4] HANI K,WEN S H,THOMAS H.Overview of the development of the solar electric propulsion technology demonstration mission 12.5-kW Hall thruster[C]∥50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland,OH,AIAA 2014-3898,2014.

[5] DAN L,RAANAN E,GAL A.CAM200 Hall thrusterdevelopment overview[C]∥Proceedings of 66th IAC, Jerusalem,Israel,IAC-15-C4.4.4,2015.

[6] CHIEN K R.L-3 communications ETI electric propulsion overview[C]∥The 29th International Electric PropulsionConference,Princeton University,October 31-November 4,IEPC2005-315,2005.

[7] SEMENKIN A V.Overview of electric propulsion activity in Russia[C]∥The 30th International Electric Propulsion Conference,Florence,Italy,September 17-20,IEPC 2007-275,2007.

[8] KOPPEL C R,MARCHANDISE F,PRIOUL M.The SMART-1 electric propulsion subsystem around the Moon:in flight experience[C]∥41st AIAA/ASME/ SAE/ASEE Joint Propulsion Conference&Exhibit,Joint Propulsion Conference,Tucson,Arizona,July 10-13, AIAA 2005-3671,2005.

[9] BRUCE E P,JOHN M P,JOHN P O.Properties of gases and liquids[M].New York:McGraw-Hill, 2001:111-163.

[10] PENG D Y,ROBINSON B D.A new two constant equation of state[J].Industry Engineering Chemical Fundamentals,1976,15(1):59-64.

[11] JOHN W D,JOSEPH C,ANTHONY D.Advanced Xenon feed system(AXFS)development and hot-fire testing[C]∥45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference&Exhibit,Denver,Colorado, August 2-5,2009,AIAA 2009-4910.

[12] GANAPATHI G B,ENGELBRECHT C S.Performance of the xenon feed system on Deep Space One[J].Journal of Spacecraft and Rockets,2000,37(3):392-298.

[13] OSBORN M F,NETWALL C J.Higher performance xenon flow system(XFS)optimized for low mass, volume and cost[C]∥45th AIAA Joint Propulsion Conference,Denver,Colorado,August 2-5,2009: AIAA 2009-4909.

[14] JACOBSEN R T,STEWART R B.Thermodynamic properties of nitrogen including liquid and vapor phases from 63 K to 2 000 K with pressure to 10000 bar[J]. Journal of Physical and Chemical Reference Data,1973, 2(4):757.

[15] ZONG N.Modeling and simulation of cryogenic fluid injection and mixing dynamics under supercritical conditions[D].Pennsylvania:The Pennsylvania State University,2005.

[16] NIST.NIST standard reference database[EB/OL].http:∥webbok.nist.gov.

(编辑:车晓玲)

A theoretical method for xenon's physical property used in electrical propulsion system

CHEN Tao*,LIU Guoxi,SONG Fei,WU Conglong
Beijing Institute of Control Engineering,Beijing 100190,China

The possible operation temperature of propellant xenon in electrical propulsion system is between-30℃and 45℃,which covers the xenon's critical temperature.At the critical temperature,xenon's state is sensitive to the operating pressure and the ambient temperature.The propellant may exhibit different forms.These characteristics make the traditional equation of state ineffective to calculate thep-V-Trelationship in the above temperature range(max error may rise to 30%).To solve this problem,a new calculation method based on the corresponding state principle was put forward for physical property estimation.The theoretical outcomes were compared with experiment data and available database.The results show that among the whole temperature and pressure range,the method is capable to predict the xenon's physical property in gas,liquid,supercritical state with an error less than 0.5%.

electrical propulsion;xenon;supercritical;corresponding state principle; physical properties;equation of state

V43

:A

10.3780/j.issn.1000-758X.2016.0018

2015-11-09;

:2015-12-25;录用日期:2016-01-18;< class="emphasis_bold">网络出版时间

时间:2016-02-24 13:42:48

http:∥www.cnki.net/kcms/detail/11.1859.V.20160224.1342.015.html

*

:陈涛(1986-),男,博士,工程师,364993478@163.com,主要研究方向为电推进系统设计

陈涛,刘国西,宋飞,等.电推进系统Xe物理特性计算方法[J].中国空间科学技术,2016,36(1):113-119.

CHEN T,LIU G X,SONG F,et al.A theoretical method for xenon′s physical property used in electrical propulsion system[J].Chinese Space Science and Technology,2016,36(1):113-119(in Chinese).

http:∥zgkj.cast.cn