一种基于MDDs的可达状态的算法研究

段珊，王金娟

（湖南涉外经济学院信息科学与工程学部，长沙 410025）

一种基于MDDs的可达状态的算法研究

段珊，王金娟

（湖南涉外经济学院信息科学与工程学部，长沙 410025）

以固定点为数学基础，多值决策图（Multi-Valued Decision Diagrams，MDDs）为存储结构来实现系统可达状态空间建立的饱和算法在异步系统的模型中显示其良好的空间和时间效应。对该算法的理论和实现方法进行详细的阐述和分析，提出通过对当前事件中的扩展链的预先判断，修改原饱和算法来实现取消无扩展链的事件的函数递归调用、新节点的内存空间的申请与回收，达到提高算法的时间和空间效率；并从理论推理和实验上进行验证。

可达状态；固定点；饱和算法；MDDs

0 引言

可达状态空间的计算与存储是形式化验证工具必需面对的关键性问题，例如模型检测器，它需要穷尽系统的所有可达状态来实现系统性质的确认。随着所研究系统的复杂化，如何构建和存储巨大的状态空间是当前数字系统一个瓶颈。以BDD[1]为代表的符号技术使符号模型检测[2]技术在同步系统中运用取得了较大的成功。但在异步系统中，由于事件行为交替执行的不确定性，它依然不得不面临空间状态的爆炸问题。

Ciardo和Andrew在SMART[3]（Stochastic Model checking Analyzer for Reliability and Timing）这个模型检测工具中采用了一种基于MDDs[4]存储结构，利用不动点理论计算可达状态的饱和算法[5-6]。该算法针对分布式异步系统的特性，通过对其高层模型的逻辑结构在MDD结构上的映射关系的定义，采用有效的迭代策略实现了可达状态空间的存储与建立。实验证明通过在一些高层次的系统模型，例如Petri网[7]，MARKOV链[8]的运用，显示了该算法比其他通用的可达状态算法（BFS和DFS）在时间上和空间上的高效[9]。本文对该算法的原理与实现进行阐述，提出了基于当前事件的扩展链的预先判断的新饱和算法，并通过理论推理和实验进行了论证。

1 系统状态模型的描述

●s：系统的初始状态。

N为各事件的迁移函数的逻辑和，即N（i）=∪а∈εNα（i），Nα：与事件α关联的迁移函数，α∈ε，ε表示系统有限的事件集合。Nα（i）为系统状态i在α事件发生时系统迁移到的状态。如果Nα（i）≠Φ表明事件α在状态i可被激活；若Nα（i）=i，表明事件α不影响状态i。

1.1 状态的符号表示与操作

饱和算法采用MDDs来实现可达状态空间的建立和存储。MDDs由一个根节点，一个或多个非终节点，两个0和1的终节点构成。与BDD不同的是，它的每个节点可以有多个取值，每个节点可以有多条引出边。与BDD相比，MDD更能直接、紧凑的描述一个由K个子系统组成的异步系统的状态。K个子系统用K个变量表示，分布在K到1层，子系统的状态值即变量的取值，系统状态的K元组（iK，…，i1）直接对应MDD的K层到1层任意路径上的变量取值。

系统的节点采用＜k，p＞形式表示，k表示节点所在的层，p为该节点在本层的唯一标识。K层只包含一个根节点，K-1到1层包含一或多个非终节点。0层有两个终节点＜0，0＞和＜0，1＞。

每个非终节点＜k，p＞可以有|?k|条引出边指向k-1或下层的节点。若有一条边，边上的值为i，i∈Sk，指向节点〈k-1，q＞，则写成＜k，p＞[i]=q。与BDD不同，MDD允许存在冗余节点，也就是他们的所有边指向同一节点，但不能存在复制节点（若同一层中节点＜k，p＞、＜k，q＞，对任意的i∈Sk，有＜k，p＞[i]=＜k，q＞[i]。这样的节点称为复制节点）。

图1为一具有四个子系统模型状态的MDD表示。

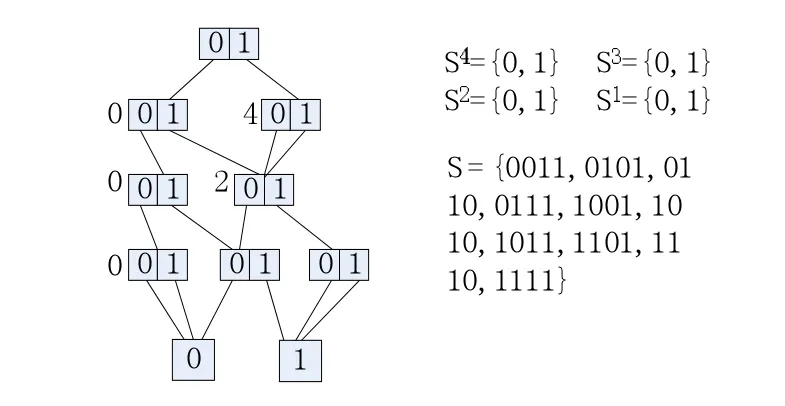
图1 一个四个变量的MDD和它表示的状态

同OBDD类似，MDD所表示的状态操作可以直接由MDD的操作简单来实现[11]，并操作是饱和算法中最常用的MDD操作，同BDD的并操作类似。

1.2 迁移函数的符号表示

基于事件的异步系统中，迁移函数反映着事件的行为。当事件α对每个子模块的作用相互独立时，事件α的迁移函数可以写成子模块的Kronecker积的形式。即Na=X…X，其中称为事件α在子模块k上的迁移函数。

迁移函数可以采用MDD描述，也可以采用矩阵MxDs（Matrix Diagrams）表示[12]。同BDD描述迁移关系类似，MDD需要用双倍数的层变量表示迁移关系。MxDs与MDDs结构类似，每一层对应一个|Sk|*|Sk|的0，1矩阵描述该层的状态变迁，行表示当前状态值，列表示下一状态值，若行列对应的迁移存在，该位置引出值为1的边指向下一层的迁移函数矩阵；如某层不存在状态变迁，该层的迁移函数I，上层的引出边可以跳过该层直接指向下层。MxDs能很好描述满足Kronecker积的事件迁移函数。迁移函数N1（001）={101}，N2（011）={111}，N3（021）={121}，N4（101）={200，201}，N5（111）={210，211}，N6（121）={220，221}。

图2 MxDs和MDDs表示迁移函数

2 饱和算法

饱和算法以固定点的数学理论为基础，基于MDDs结构模型的节点迭代算法。从初始状态的MDD出发，按一定的顺序迭代使用事件的迁移函数扩展状态来实现可达状态空间建立，直到不再增加新的状态。

饱和算法是以事件的迁移函数满足Kronecker积为条件的，对系统中不满足该条件的事件，可以通过合理的分解、合并来达到这一要求[12]。另外为了减少饱和算法迭代次数，往往依据事件对层的依赖关系对事件进行分类，为此提出一些相关概念。

对所有i∈Sk，若（i）=i，则α不依赖k层，=I。若存在i，j∈Sk，（i）≠j，α依赖k层，≠I。

εk={α∈ε:First（α）=k}最高依赖层为k的事件集合；

N*≤K:top（α）≤k的事件的迁移函数。

2.1 饱和算法实现

定义1饱和节点，一个MDD节点B＜k，p＞在k层是饱和的，当且仅当对所有α∈{α：top（α）≤k}事件的执行不会为该节点增加任何新状态，B（＜k，p＞）=（B（＜k，p＞）成立。

推论1：若B＜k，p＞节点是饱和的，则这从＜k，p＞点所能到达的节点都是饱和的。

推论2：若B＜k，p＞，B＜k，q＞两节点是饱和的，则B＜k，p＞∪B＜k，q＞是饱和的。

为了减少节点饱和中的递归次数，尽可能先饱和下层节点。饱和算法的基本方法自下而上依次饱和节点。

①建立一个L层的MDD，表示系统的初始状态s。

②将第一层的节点饱和化，执行ε1事件的变迁函数（i）扩展节点；

③将第二层的节点饱和化，执行ε2中事件的变迁函数（i）扩展节点；如果在第一层创建了新的节点，同时将它饱和化；

④将第三层的节点饱和化，执行ε3中事件的变迁函数（i）扩展节点；，如果在第二层、第一层创建了新的节点，同时将它们饱和化；

⑤将L层根节点饱和化，通过执行εL中事件的变迁函数（i）扩展节点；，若在第L-1，L-2，…层创建了新节点，同时将它们饱和化。

为了简单起见，本文中只对单个节点的饱和算法进行了描述，并不对整个系统状态节点生成进行描述。

算法主要由两个函数来实现，Saturate（＜k，p＞）使用α∈εk事件来饱和B＜k.，r＞节点时，先通过调用Recfire函数递归调用完成下层节点在α事件下的扩展饱和，然后再返回该层实施该层的节点饱和。

为降低算法复杂度，算法中定义一些相关的hash表对饱和算法中的运算结果和中间过程进行记录。唯一表UT[k]，存放k层唯一节点，对于已饱和化的k层节点，先检查UT[K]表，若该节点已存在，则删除新饱和化的节点，返回表中的原节点，否则新节点插入UT[K]表；k层的并运算表UC[K]，存放＜k，p＞、＜k，q＞并运算后的返回结果＜k，s＞，即B（k，s）=B（k，p）∪B（k，q）；FC [k]记录k层的已扩展的节点，＜k.q＞在α事件的作用下建立新的并饱和化的节点＜k，s＞后（注意First（α）＞k，并且B（k，s）=（Nα（B（＜k，p＞）））），要将条目（FC[k]，{q，e}，s）插入FC[k]中。以便下次需要扩展时，不需要重复计算，根据从该条目直接返回结果。

2.2 新饱和算法

饱和算法的时间和空间效率取决于符号状态产生的迭代次数。迭代的次数与当前状态、事件迁移函数密切相关。实际系统中引发当前状态变迁的事件往往是少数，事件对节点进行状态扩展饱和之前，判断该事件中是否存在扩展链，减少无扩展链的迭代是提高饱和算法效率的方向之一。

定义2可扩展状态，节点＜k，p＞中存在状态i，＜k，p＞[i]≠0，且[i，j]≠Ф，则称i为α事件的可扩展状态。

＜k|p＞[i]称为当前结点，由当前节点中的可扩展状态指向的下层节点为下层的当前节点。

定义4扩展链，若α事件在所有k层（last（α）≤k≤top（α））的当前节点中存在α事件的可扩展状态，则α事件中存在扩展链。

扩展链的依据是事件的迁移函数满足Kronecker积为条件。

只有α事件中存在当前状态的扩展链，才能实现当前状态的扩展饱和。原饱和算法是通过Recfire函数的递归调用来实现对下层当前节点的扩展。在递推过程中若遇到某层当前节点为非扩展状态，即刻依次返回到最初调用点。最坏的情况是递推深入到k=last（α）层时，当前节点中不存在α事件的可扩展状态，则必须从该层开始逐层向上返回退出，显然此时前面的调用都是无效调用，创建的新节点也需依次回收。

为了减少这种无效的迭代调用，本文提出在用α事件对当前节点B＜k，p＞扩展饱和之前，先确认它是否存在扩展链。若是，则调用Recfire函数的依次进入当前节点下层，进行扩展。若不是，则不进入。进入Recfire函数后，要穷尽该当前节点中所有可扩展状态，并对下层的不同节点的分支扩展链进行判断和提取，若不存在及时退出，存在则继续进入不同分支，以便在返回时穷尽所有可能饱和所有节点。根据这样的思想在Saturate和Recfire函数中引入了一个新的函数Even_Enable，并对这两个函数实现做相应的修改。

Even_Enable函数描述了α事件在＜k|p＞节点是否存在扩展链的判断算法。其基本思想从＜k|p＞节点开始对当前节点的可扩展状态进行搜索，若存在则直接进入该当前节点的各下层当前节点进行搜索，重复这个过程，直到到返回false或者1；查找扩展链时只要找到当前节点的一个扩展状态后就进入当前节点的下层，若当前分支节点无扩展状态，则进入当前节点的另外一节点，进入另一分支继续寻找。

如果能进入k=last（α）-1层，则当前节点＜k|p＞存在扩展链，返回1，否则就会在穷尽了某层的当前结点的所有分支后返回false，＜k|p＞节点无扩展链。

扩展链的提前判断，减少Recfire无效调用的次数和内存空间的申请与回收，从而提高时间、空间效率。

//Ecng当前分支扩展链标识；

Saturate函数的修改，实现了无扩展链事件的及时退出；Recfire函数的修改保证了对下层扩展链分支进行及时判断和提取，若不存在分支链，退出分支扩展链，否则同时进入不同的分支链，既消除了无扩展链分支的进入也保证了尽可能饱和所有下层节点。

2.3 算法验证

下面实例直观的呈现了利用新饱和算法实现可达状态的MDDs的建立过程。实例初始状态为（0，0，0，0），各事件对状态的影响及迁移函数见下表。

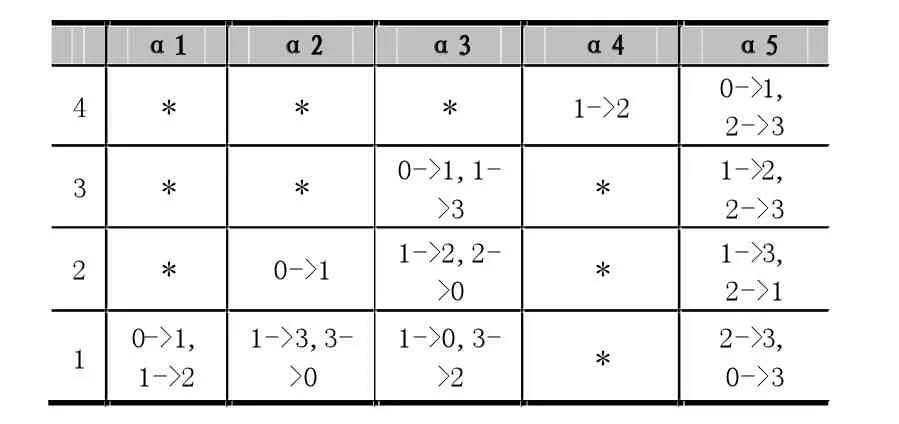
表1 事件迁移表

“*”表示该层不受事件的影响，迁移函数的表示见图3。

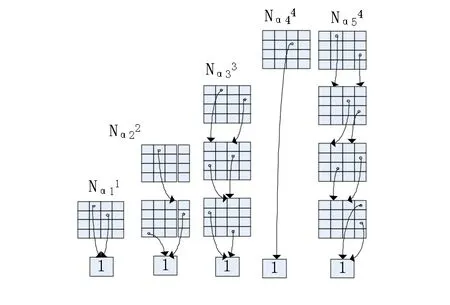
图3 迁移函数的MxDs表示

图4用图示的方法直观的展示了新饱和算法完成可达状态空间的建立过程。

①系统的迁移函数的MxDs如图3。初始状态（0，0，0，0）的MDD表示如图4-a。

②依据饱和算法首先从从底部的节点＜1，1＞开始，该节点中存在可扩展状态0，事件α1存在有效扩展链，直接调用Recfire函数扩展了当前节点＜1，1＞，增加了两个状态1，2。见图（4-b）;

③饱和＜2，1＞节点，该节点中存在α2的可扩展状态0，Evalid（1，＜2，1＞[0]，Nα21）返回1，α2中存在扩展链。Saturate函数调用Recfire（α2，1，＜2，1＞[0]）在下层创建新的节点＜1，2＞，第一层的当前节点＜2，1＞[0]存在α2的可扩展状态1，Recfire自身调用Recfire（α2，0，＜1，1＞[1]），因k=0＜last（α），从本层结束递推并开始向上返回，返回中完成本层新建节点＜1，2＞的状态3添加和饱和。并将已饱和的节点在FC[1]表中进行记录。见图4-c。

④Saturate（3，1＞，该节点中存在α3的可扩展状态0，Saturate调用Evalid（2，＜3，1＞[0]，Nα32）函数，返回值1，判断α3中存在扩展链，调用Recfire进入下层节点的扩展和饱和。依次在第一层、第二层建立了新的节点＜1，3＞、＜2，2＞，并将它们饱和，在FC[1]、FC[2]表中进行记录。返回到节点＜3，1＞后，节点新状态1成为α3的可扩展状态，Saturate再次调用Evalid（2，＜3，1＞[0]，Nα32）函数，返回值0，表明当前状态下，α3不存在扩展链，返回。重复④直到没有新的节点产生。见图4-d。

⑤同样方法用α4，α5对节点＜4.1＞进行饱和，最终的状态空间的MDDS如图4-e。

图4 饱和算法执行

最后的可达状态空间{0000，0001，0002，0013，0122，1213，2213}

上述饱和过程采用了新饱和算法，在Saturate函数还没调用Recfire函数之前，一次性的利用Evalid函数来判断当前事件中是否存在扩展链。若有，则调用Recfire函数进入下层当前节点的做进一步分支扩展链判断。否则及时退出。

用C语言对新算法和原算法进行了编程实现，并在多个典型事例上运行，统计了两种算法中调用Recfire函数的次数。

表2列出了几个实例运行中的Recfire函数的调用情况，一般来说系统中的层变量越多，当前无扩展链情况越多，新算法的优越性越明显。

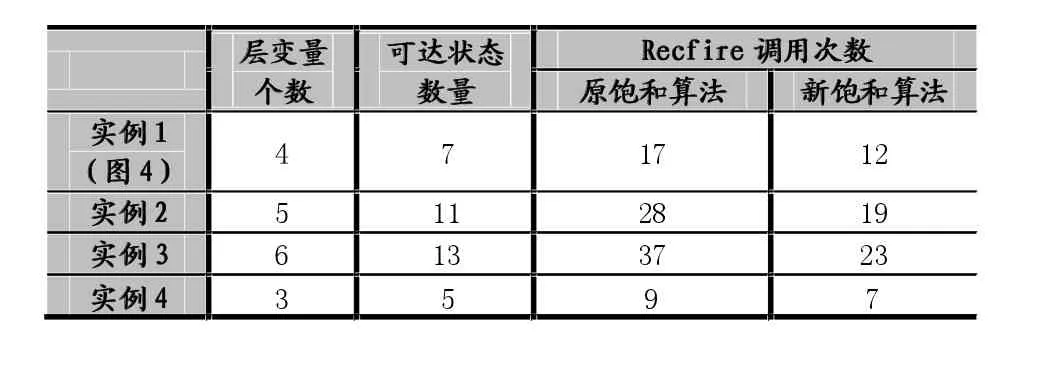
表2 实例运行结果

3 结语

Ciardo、Andrew提出的以固定点为依据、基于MDD结构的饱和算法在异步系统模型例如Petri Net、Markov链等中显示它较好的空间和时间特性。本文详细的阐述了饱和算法理论依据、实现方法；提出了通过对当前事件的扩展链进行预先判断，只有在当前事件中存在扩展链时才用Recfire函数来继续下层节点分支扩展链的提取判断，以便回归时进行扩展、饱和；取消无扩展链的事件的Refire函数的递归调用、新节点的内存空间的申请与回收，理论推理分析和实验证明了新饱和算法的有效性。

[1]R.E.Bryant.Graph-Based Algorithms for Boolean Function Manipulation.IEEE Trans.Comp.，35（8）:677-691，Aug.1986.

[2]J.R.Burch，E.M.Clarke，D.E.Long.Symbolic Model Checking with Partitioned Transition Relations.In A.Halaas and P.B.Denyer，Editors，Int.Conference on Very Large Scale Integration，pages 49-58，Edinburgh，Scotland，Aug.1991.IFIP Transactions，North--Holland.

[3]G.Ciardo，R.L.Jones，A.S.Miner，R.Siminiceaunu.Logical and Stochastic Modeling with SMART.In Proc.Modelling Techniques and Tools for Computer Performance Evaluation，LNCS 2794，pages 78-97，Urbana，IL，USA，Sept.2003.Springer-Verlag.

[4]T.Kam，T.Villa，R.Brayton，A.Sangiovanni-Vincentelli.Multi-Valued Decision Diagrams:Theory and Applications.Multiple-Valued Logic，4（1-2）:9-62，1998.

[5]Ciardo，G.，Marmorstein，R.，&Siminiceanu，R..The Saturation Algorithm for Symbolic State-Space Exploration.International Journal on Software Tools for Technology Transfer，8（1），4-25，2006.

[6]Andrew S.Miner.Saturation for a General Class of Models.IEEE Trans.Softw.Eng.，32（8）:559-570，August 2006.

[7]吴哲辉.Petri网导论.北京：机械工业出版社，2006.4

[8]Min Wan，Gianfranco Ciardo，Andrew S.Miner.Approximate Steady-State Analysis of Large Markov Models Based on the Structure of Their Decision Diagram Encoding.Perf.Eval.，68（5）:463-486，2011.

[9]G.Ciardo，R.L.Jones，A.S.Miner，R.Siminiceanu.Logical and Stochastic Modeling with SMART.Perf.Eval.，63:578-608，2006.

[10]P.Buchholz，G.Ciardo，S.Donatelli，P.Kemper.Complexity of Memory-Efficient Kronecker Operations with Applications to the Solution of Markov Models.IN-FORMS J.Comp.，12（3）:203-222，2000.

[11]T.Kam，T.Villa，R.Brayton，A.Sangiovanni-Vincentelli.Multi-Valued Decision Diagrams:Theory and Applications.Multiple-Valued Logic，4（1-2）:9-62，1998.

[12]Andrew S.Miner.Implicit GSPN Reachability Set Generation Using Decision Diagrams.Perf.Eval.，56（1-4）:145-165，March 2004.

Research on the Algorithm for Reachable State Based on MDDs

DUAN Shan，WANG Jin-juan

（Hunan International Economics University，Changsha 410205）

On the mathematical basis of fixed point,MDDs are good for storage structure to realize the computation of reachable state space;the saturation algorithm shows its good in space and time effect in asynchronous system.Presents the theory and implementation method of the algorithm in detail and analysis,and puts forward a method that prejudge extension chain of the current event,modifies the original saturate event to call for recursive function to realize the expansion of the lower nodes and saturation algorithm to cancel the calling for function,applying and recycle of new node for memory without extension chain,so as to improve the efficiency of the algorithm of time and space.The new method is proved from the theoretical analysis and experiment.

Reachable State Space;Fixed Point;Saturation Algorithm;MDDs

1007-1423（2016）35-0043-07

10.3969/j.issn.1007-1423.2016.35.009

2016-11-22

2016-12-05

段珊，硕士，研究方向为形式化验证、高性能计算

王金娟（1981-），女，湖南长沙人，硕士，系统分析师，研究方向为软件工程技术与应用