例谈学生数学解题中的思维品质

□陈朝阳

（杭州市余杭区教育局教研室，浙江杭州 311100）

例谈学生数学解题中的思维品质

□陈朝阳

（杭州市余杭区教育局教研室，浙江杭州 311100）

通过数学解题的具体案例，从学生的思维品质视角深入分析，剖析学生思维深刻性、灵活性、独创性、批判性、敏捷性的本质，引发教师对学生思维品质培育的关注与思考.

思维品质；深刻性；灵活性；独创性；批判性；敏捷性

思维品质反映了每个个体智力或思维水平的差异，主要包括深刻性、灵活性、独创性、批判性、敏捷性等.优秀的思维品质来源于优秀的逻辑思维能力.数学解题除了检测学生的数学知识与方法掌握的程度与水平，也检测学生思维品质的层次与特征，从数学解题中来剖析学生的思维品质，可以更加深刻地揭示数学思维本质特征[1].在数学教学与辅导中，不断地发现学生在数学解题中的一些现象，这些现象从人的思维角度去认识，可以把握问题的本质，关注并改善教学中的重要环节，有利于提升对数学教学的认识.

一、仔细审题：读出问题背后本质，体现思维的深刻性

例1.已知数列{an}满足：则a1a2a3…a17a18=_______；设bn=（-1）nan，数列{bn}前n项的和为Sn，则S2016=_______.

心理特征：“一步登天”急功近利思想对学生的深刻影响.

心理特征：三步就想找到答案——仍是急功近利思想对学生的深刻影响.

心理特征：审题不细作怪，思维定式影响.

追根求源：数学思维的深刻性是指思维活动的抽象程度和逻辑水平，涉及思维活动的广度、深度和难度.学生面对感性材料（题设条件），去粗取精、去伪存真，由此及彼、由表及里，进而抓住事物的本质与内在联系，认识事物的规律性.个体在这个过程中，表现出深刻性的差异.思维的深刻性集中表现为在智力活动中深入思考问题，善于概括归类，逻辑抽象性强，善于抓住事物的本质和规律，开展系统的理解活动，善于预见事物的发展进程.超常智力的人抽象概括能力高，低常智力的人往往只是停留在直观水平上[2]19.数列中递推思想是非常重要的，它反映了数列的本质特征，由特殊起步，一步一步地向着本质属性走去，为什么学生不重视递推思想方法呢？因为低思维层次的学生，只会代公式计算，不知道或不理解项与项之间的联系的重要性.

二、解法探索：寻找内部结构关系，体现思维的灵活性

现象1：对于第（1）题，有学生考虑函数定义域[-1，1]，将端点值代入得到值域为把给定函数认定为单调函数.

心理特征：心理潜意识是求值域必须考虑定义域，但当遇到无理式时不知如何处理，于是就代入求值.

现象2：建立在错误观点下的推理，有学生认为“2x-1是奇函数”，“2x+1是奇函数”，然后利用“奇÷奇=偶”判断为偶函数.

心理特征：在错误心理暗示下的学习心理活动导致判断出错，是数学解题中最常见的现象.

现象3：建立在特殊值代入的推理，虽然由x=0得y=2得到一个点（0，2）与答案吻合，但推理无数学基础，展现出一种盲目的思维.

心理特征：在面对一个无知概念时的特殊值处理，是数学逻辑思维能力弱者常用的方法.

追根求源：灵活性是指思维活动的灵活程度.它的特点包括：一是思维起点灵活，即从不同角度、方向、方面，能用多种方法来解决问题；二是思维过程灵活，从分析到综合，从综合到分析，全面而灵活地作“综合的分析”；三是概括—迁移能力强，运用规律的自觉性高；四是善于组合分析，伸缩性大；五是思维的结果往往是多种合理而灵活的结论，不仅仅有量的区别，而且有质的区别[2]25-27.灵活性反映了智力的“迁移”，如我们平时说的，“举一反三”、“运用自如”等.灵活性强的人，智力方向灵活，善于从不同的角度与方面起步思考问题，能较全面地分析、思考问题，解决问题.审题是解题的基础，而观察又是审题的必要前提.

一是观察题设中主要条件有没有代数结构？代数结构有几何意义吗？[3]如上述第（1）题表示上半圆，函数表达式结构与斜率公式结构一致，所以代数结构的几何意义就是上半圆上的点与定点（2，1）连线斜率的范围.

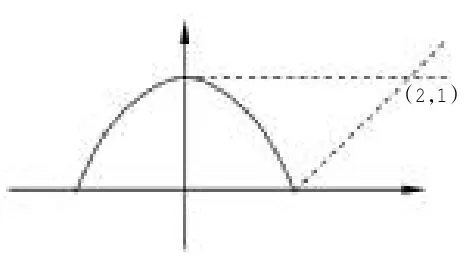
二是看问题前后条件之间是否有某种联系，寻找到这一关联就找到问题的答案，如第（2）题，“为奇函数”，所以，此函数的对称中心是原点，后者的对称中心就是（0，2）.

三、途径合理：养育良性运算习惯，体现思维的独创性

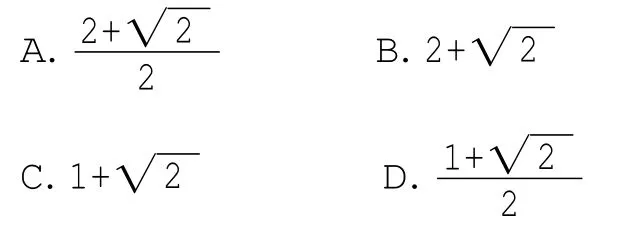
例3.若抛物线y2=2px（p＞0）的焦点为F，其准线经过双曲线的左焦点，点M为这两条曲线的交点，且|MF|=p，则双曲线的离心率为（ ）

追根求源：独创性即思维活动的创造性.在实践中，除善于发现问题、思考问题外，更重要的是要创造性地解决问题.独创性源于主体对知识经验或思维材料高度概括后集中而系统的迁移，进行新颖的组合分析，找出新异的层次和交结点.概括性越高，知识系统性越强，伸缩性越大，迁移性越灵活，注意力越集中，则独创性就越突出.

（1）每个人都有自己的运算习惯，但如果运算习惯是不良的，在各种数学测试时，运算要花费大量时间.

（2）数学运算是数学思维的核心部分，具有独创性的运算次序就是要寻找最简、最优的符合运算规则的思维，这一方面，在基础数学教育中存在问题很多，值得进一步深入研究.

四、过程监控：甄别推敲步步为营，体现思维的批判性

例 4.设实数 x1，x2，…，x100满足：|x1|=9，|xn|=|xn-1+1|，n=2，3，4，…100，则x1+x2+…+x100的最小值是___________.

现象1：|x1|=9，|x2|=8，…，|x9|=1，|x10|=0，|x11|= 1，|x12|=0，把求x1+x2+…+x100理解为求|x1|+|x2|+…+|x100|，然后填写90.

心理特征：问题没有审好，就急于下笔；在消极思维定式的引导下犯错.

现象2：认为x1=-9，x2=-8，…，x9=-1，x10= 0，x11=1，x12=2，…认为最小值是-9×100+

心理特征：当面对一组数呈现一个等差数列规律时，就在思维定式的误导下，走入歧途.

解析：在递推过程中，步步寻找最小者，|x1|=9，x1=±9，取x1=-9，同理x2=-8，…，x9=-1，x10=0；|x11|=1，|x11|=±1，取x11=-1，代入可得x12= 0，发现周期性，x13=-1，x14=0，于是x1+x2+…+x100=

追根求源：批判性是思维活动中独立发现和批判的程度.这是思维过程中一个很重要的品质.思维的批判性品质，来自于对思维活动各个环节、各个方面进行调整、校正的自我意识.它具有分析性、策略性、全面性、独立性和正确性等五个特点.正是有了批判性，人类才能够对思维本身加以自我认识，也就是人类不仅能够认识客体，而且也能够认识主体，并且在改造客观世界的过程中改造主观世界.现象1的学生没有理解题意就急于做题，不仅没有独立发现的思维特征，也不具备批判性的思维意识.现象2的学生没有坚持到底，进入x11时出错，主要是思维定势作怪.事实上，本题的最后数据构成前10项为等差数列，后90项为周期数列.

五、改变视角：同一问题不同方法，体现思维的敏捷性

例5.在棱长为1的正方体ABCD-A1B1C1D1中，点P是正方体棱上一点（不包括棱的端点），且，则满足条件的点P的个数为____.

解析1：画出正方体图.

正方体共有12条棱，其他6条棱上是否有满足条件的点呢？

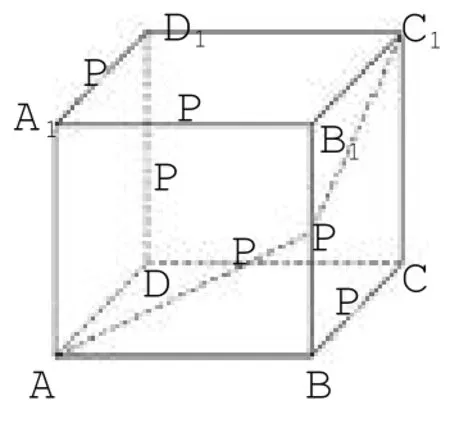
假设满足条件 P在CC1，使 CP=x，则，解得故在其他六条棱上也存在满足条件的点，故共有12个满足条件的点.

追根求源：敏捷性是指思维活动的速度，它反映了智力的敏锐程度.有了思维敏捷性，在处理问题和解决问题的过程中，能够适应变化的情况来积极地思维，周密地考虑，正确地判断和迅速地做出结论.比如，智力超常的人，在思考问题时敏捷，反应速度快；智力低常的人，往往迟钝，反应缓慢；智力正常的人则处于普通的速度.

问题的两种不同的思考，反映着学生思维的敏捷程度不同，解析1建立在对数字的敏感性，，这正是棱的中点满足的数量关系.此思路容易认为此问题的答案为6.

因此，在解题过程中与学生一起研究、探索、发现、解决由一种性质所引申出来的变式，给学生充分表现自己、发挥想象力的机会，使其在解题中感到无穷乐趣，从而有意想不到的创造性表现[4].所以说为了使学生在学习数学有关知识后，能进行数学教学问题的“再创造”，教师选择和设计一些问题的引申与推广渗入课堂教学中，可激发学生的探求欲望，对学生的创造性思维能力的培养有着特殊的功能.

［1］任樟辉.数学思维论［M］.南宁：广西教育出版社，1996：16.

［2］吕凤祥.中学数学解题方法［M］.哈尔滨：哈尔滨工业大学出版社，2003.

［3］陈朝阳.挖掘代数结构 渗透数学思想——2014年浙江省高考文科第16题解法探究［J］.中学数学，2015（2）：93.

［4］陈朝阳.问题串与解法串个性化结构设计的思考［J］.中学教研（数学），2015（5）：9.