从感性到理性 凸显数学的实验味——以数学实验“数格点算面积”教学设计为例

□杨丽娟

（昆山市葛江中学，江苏昆山 215300）

从感性到理性 凸显数学的实验味
——以数学实验“数格点算面积”教学设计为例

□杨丽娟

（昆山市葛江中学，江苏昆山 215300）

结合苏科版数学教材八年级下册实验课《数格点 算面积》的课堂教学，通过探究格点多边形的面积S与多边形边上的格点数L及它内部的格点数N之间的数量关系，对如何帮助学生理解数学，凸显数学的实验味有如下理解：通过实验操作，获得感性经验；验证实验结果，培养推理能力；表述实验结论，提升数学理解；获得实验感悟，实现课堂价值.

数学实验；感性经验；推理能力；数学理解；课堂价值

《义务教育数学课程标准（2011年版）》指出：“学生学习应当是一个生动活泼的、主动和富有个性的过程.认真听讲、积极思考、动手实践、自主探索、合作交流等，都是学习数学的重要方式.学生应当有足够的时间和空间经历观察、实验、猜测、计算、推理、验证等活动过程.”[1]所谓数学实验是指为研究与获得某种数学理论、验证某种数学猜想、解决某种数学问题，运用一定的物质手段，在特定的实验条件下进行的一种数学探索活动.与物理、化学实验相比，思维量大是数学实验的显著特征.数学实验教学就是恰当运用数学实验，通过实践操作、探索交流，从而发现规律、提出猜想、验证猜想的数学活动.

2016年5月苏州市初中数学实验教学研讨活动在苏州市工业园区星海实验中学开展，笔者观摩了研究课《数格点 算面积》，这是苏科版八年级下册安排的实验15，本节课主要探究格点多边形的面积S与多边形边上的格点数L及它内部的格点数N之间的数量关系，通过画图、列表、分析数据、寻找规律，发现皮克定理.结合《数格点 算面积》的课堂教学，对如何帮助学生理解数学，体现数学的实验味有以下的一些感悟.

一、通过实验操作 获得感性经验

数学实验是通过动手动脑“做”数学的一种学习活动，是学生运用有关工具（如纸张、剪刀、模型、测量工具、作图工具以及计算机等），在数学思维活动的参与下进行的一种以学生人人参与的实际操作为特征的数学验证或探究活动[2].感性经验是通过感觉器官对客观事物现象及外部联系的认识经验，数学实验以“做”为支架，通过实际操作获得亲身体验，积累感性经验.

（一）巧设问题情境 说明实验操作的必要性

问题情境是常用的营造良好课堂氛围的有效手段，教学中以学生已有的生活经验为基础创设问题情境，准确获取数学信息，借助实验操作解决问题，以此提高学生对知识探索的欲望，培养学生用数学思想解决问题的能力.

本课设计的问题情境：兄弟分地.

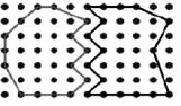
图1

如图1，哥哥说：“我的地一圈只有15棵树，而弟弟的地一圈有17棵树，弟弟的面积大！”弟弟说：“我的地里只有16棵树，而哥哥的地里有17棵树，哥哥的面积大！”到底谁的话有道理？

分析：在这个问题情境中，分出来的两块地就是两个格点多边形，地的面积即格点多边形的面积S，圈上的树即多边形边上的格点数L，地里的树即多边形内部的格点数N.学生要判断兄弟俩所说的话正确与否，就需要探究S、L、N之间的关系，需要通过实验操作来验证.

（二）开展系列探究活动 循序渐进获得感性经验

在平时的学习中，学生习惯研究两个变量之间的关系，现在要探究S、L、N三个变量之间的关系，对学生是一种新体验，为此设计了四个探究活动.

活动一：探究当格点多边形内部的格点数N=0时，格点多边形的面积S与边上的格点数L之间的数量关系.

如图2，①②③都是N=0的格点多边形，课堂上师生合作探究，通过画图、列表、分析数据，发现当N=0时，

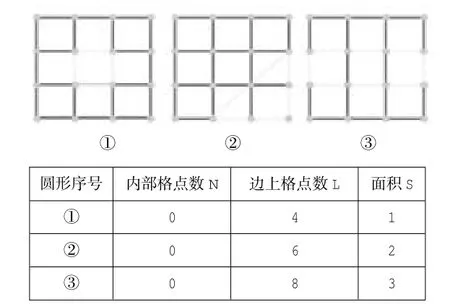
图2

活动二：探究当格点多边形内部的格点数N=1时，格点多边形的面积S与边上的格点数L之间的数量关系.

活动三：探究当格点多边形内部的格点数N=2时，格点多边形的面积S与边上的格点数L之间的数量关系.

活动四：探究当格点多边形内部的格点数N=3时，格点多边形的面积S与边上的格点数L之间的数量关系.

说明：活动二、三、四采用学生分组探究，通过分配实验任务，让所有学生参与进来，模仿N=0的探究过程进行操作，最后汇总探究结果：当N=1时，；当N=2时，1；当N=3时，，由此得到S、L、N之间的关系

分析：设计系列探究活动，让学生充分体验“控制变量法”的运用，学生通过动手操作、观察类比、分析归纳、猜想、合作交流，经历从特殊到一般的过程，循序渐进地获得了感性经验.“控制变量法”是解决多变量问题的一种思维方法,采用“控制变量法”探究问题，分析实验数据时，要分清哪些因素是自变量，哪些因素是因变量，注意两个变量之间的因果关系.

二、验证实验结果 培养推理能力

著名数学家波利亚曾说过：“在数学领域中，猜想是合理的，是值得尊重的，是负责任的态度.在有些情况下，猜想比教会证明更重要，有了猜想，更能激发学生的探索欲望.”[3]但只有猜想而无法验证是空想，因此由探究活动得到S、L、N之间的关系还需验证这个实验结果，体现数学的严谨性.

（一）直接观察

在数学教学中，学生观察的对象是图形、数量关系、逻辑过程等.这里我们利用图2所列表格，抓住变量S与L之间的变化，发现S=

（二）描点连线

因为当N=0时，N是确定的，变量只有S与L，两个变量可以联系我们学过的函数图象来研究，将有序实数对（L，S）作为点的坐标，在平面直角坐标系中描出，发现所描的点都在一直线上，由此猜想S是L的一次函数.

（三）计算验证

在猜想获知S是L的一次函数后，设S= kL+b（k≠0），把有序实数对（4，1）、（6，2）代入，求得，即.然后把有序实数对（8，3）代入验证关系式正确.

分析：对于动手操作、猜想获得的数学结论不可替代推理论证，必须利用“数学工具”再进行逻辑验证.我们通过观察发现，利用描点连线发现是一直线，最终采用计算得以验证，在此过程中培养学生严谨的数学推理能力.

三、表述实验结论 提升数学理解

数学实验探究的最终任务，除了对探究过程中所收集的数据进行分析和处理，从而得出某些规律、找到某种关系外，准确表述实验结论，是实验探究的一个重要环节.

本节课，教师最后引导学生通过数学实验得到S、L、N之间的关系：，用语言表述为：如果格点多边形的面积为S，多边形内部格点数为N，它边上的格点数为L，那么S与N、L之间存在如下的数量关系：1.这个公式被称为“皮克定理”，是奥地利数学家皮克在1899年发现并进行证明的.该定理被誉为有史以来“最重要100个数学定理”之一.

数学理解是对于具体数学问题的解决而言，包括明白问题的条件与结论，弄清由条件到结论每一步骤的依据，领悟体现步骤与过程的思想方法，用获得的结论或方法解决其他问题，并作变通与推广.数学是文字兼数字与符号的结构体系，提高对数学语言的理解可以培养对“数与符号”的理解，在数学试验中，强调用语言表述实验结论，可以提高学生的概括能力，最终提升学生的数学理解.

四、获得实验感悟 实现课堂价值

《数格点 算面积》这节课学生通过特定的数学实验，直观地了解“皮克定理”，最后师生利用“皮克定理”解决情境引入中兄弟分地的问题，从而加深“皮克定理”的应用背景，化枯燥为有趣，增加了学生学习数学的兴趣，也为本节数学实验课画上完美句号.观摩这节数学实验课，有太多的实验感悟，虽然课堂上教师没有时间让学生倾诉，但如何借助数学实验课实现课堂价值留给我们诸多的思考.

（一）育人价值——学生知情和谐发展

借助数学实验，教师有目的有计划地引导学生主动地进行认识活动，循序渐进地掌握数学基本知识和基本技能，促进学生知情和谐发展：实验过程中，学生会遇到挫折和失败，可以培养学生克服困难的信心；用小组合作的方式进行实验，可以培养学生团队合作精神和人际交往能力；通过数学实验，学生亲身体验数学、理解数学，可以使学生由接受性学习转变为探索性学习，增强学生学习数学的主动性.

（二）教学价值——教学过程完整体现

教学过程是一种特殊的认知过程，是学生学习知识和修养道德的统一过程.数学实验课教学，学生在教师的引导下，从问题情境出发，设计合理的实验步骤，通过一系列探索性研究，发现数学规律，提出猜想并进行证明或验证，最后运用获得的结论解决数学问题，正是数学教学过程的完整体现.

（三）课程价值——课程资源深度挖掘

《基础教育课程改革纲要》指出：要重视教学在课程资源的开发与利用中的积极作用.数学课程资源是指依据数学课程标准所开发的各种教学材料以及数学课程可以利用的各种教学资源、工具和场所，因此数学实验在课程资源的开发利用过程中起着不可忽视的作用.数学实验教学中，运用有关工具，在特定的实验条件下进行数学活动，通过探究活动发现数据的变化、探索数学规律、进行推理验证、解决数学问题，就是对课程资源进行选择、组合、加工，是课程资源的深度挖掘.

（四）师培价值——教师水平有效提升

数学实验教学加大了教学目标的范围与深度，是新课程改革的体现.数学实验教学让教师重新审视传统的教育教学模式，积极探索各种有效的教学补充形式，使教学水平和教学效果不断提升.（1）提升教师教学理念，关注学生数学核心素养的培养.通过数学实验教学的研究，使教师意识到培养学生数学核心素养比培养成绩更重要，由以往关注学生解题能力升华为培养学生综合能力.（2）改善教师教学方法，重视学生的感受和体验.通过数学实验教学，教师更加尊重学生的个体差异，根据学生的认知特点和经验基础，探索初中数学实验课教学模式，学会展示知识发生发展的过程，有助于形成开放性和自主性的数学教学方式.

［1］中华人民共和国教育部.义务教育数学课程标准（2011年版）［S］.北京：北京师范大学出版社，2012：2.

［2］董林伟.数学实验：促进初中生数学学习的一种有效方式［J］.中国数学教育，2012（9）：2.

［3］王晓静.让“数学猜想”贯穿数学学习的生命线［J］.数学学习与研究，2012（5）：70.