火炮身管传热数值模拟及温度分布规律

徐 达， 罗 业， 范文博

(装甲兵工程学院兵器工程系， 北京 100072)

火炮身管传热数值模拟及温度分布规律

徐 达， 罗 业， 范文博

(装甲兵工程学院兵器工程系， 北京 100072)

为研究小口径火炮身管在不同射击条件下的温度分布特性，建立了膛内运动及后效时期火药燃气的温度方程，确定了传热初始条件；分析了内弹道时期身管膛壁对流换热系数，明确了传热边界；依据传热学理论，建立了火炮身管的传热学模型，并采用有限差分方法对模型进行了求解。最后，以某30mm小口径镀铬身管为例分析了单发及连发射击条件下温度场的分布及其变化规律，同时得到铬层附近温度梯度不显著的结论，为下一步开展小口径火炮身管寿命问题的研究奠定了基础。

火炮身管； 传热； 数值模拟； 温度分布； 铬层

火炮是以发射药为能源发射弹丸的身管射击武器[1]。在射击过程中，造成内膛形状和尺寸发生变化的因素有热、化学和机械3种，实践[2-4]证明：膛内热作用对炮膛烧蚀磨损的影响最大。膛内传热会造成膛面的烧蚀、身管的软化及热变形，对弹丸射击初速、射击精度、射击频率及身管强度等都将产生显著影响[5-7]。基于烧蚀磨损的火炮身管失效理论[8-12]认为：火药燃气的热作用是造成内膛烧蚀磨损、弹道性能丧失和身管寿命终止的主要因素。因此，对身管进行传热分析是揭示身管烧蚀磨损机理、计算烧蚀磨损量和研究身管寿命问题的前提；而对于内膛镀铬身管，由于铬层与基体钢的热导率不同，分析其交界面处的传热规律对分析铬层脱落及破坏机理具有重要意义。笔者以30mm小口径火炮镀铬身管为例，结合传热学理论对身管的传热过程进行数值模拟，并分析不同射击条件下温度场分布及其变化规律。

1 身管传热模型

火炮射击过程在极短的时间内完成，具有瞬时性和非定常特性。高温、高压和高气流速度的特点使得燃气密度、压力、温度、流速及膛壁温度等内膛参数呈动态及非线性，且均为时间及位置的函数。理论上火炮身管的热传导是一个二维不稳定的传热过程，朱文芳等[13]研究表明：温度沿径向变化较快，且沿径向方向的温度梯度一般是轴向方向的1 000倍以上，即热传导是弹丸行程的弱函数。因此，实际中常忽略热量沿轴向的传递过程，将问题简化为一维径向不稳定传热问题。在火炮射击过程中，沿身管径向方向的传热过程如下：射击时通过膛内火药燃气的强制对流作用，火药燃烧释放的热量穿过热边界层逐渐传递到身管，通过热传导不断将热量传递到外壁，外壁温度逐渐升高；之后，通过自然对流的方式，热量逐渐被环境气流带走。身管传热物理模型如图1所示，其中：T0、T1、Tw、Tv分别为环境气流温度、燃气气流温度、膛壁温度及身管外壁温度；h1、h2分别为燃气气流、环境气流与膛壁的对流换热系数。

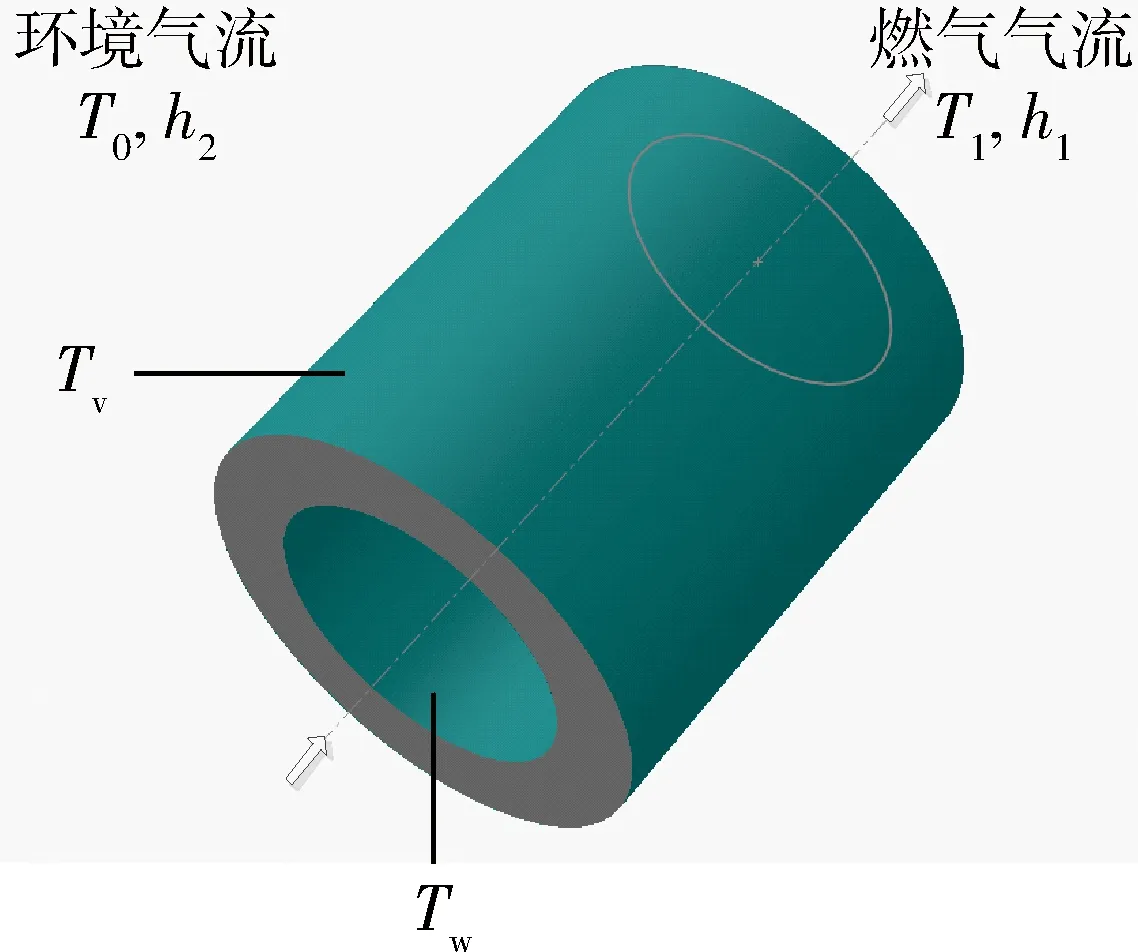
图1 身管传热物理模型

1.1 身管传热控制方程

对身管传热过程进行如下假设[14]：1)身管热传导是一个一维径向不稳定传热问题；2)身管材料为常物性，即比热容、传导率及密度等参数是定值；3)身管内温度场具有角度和轴向对称性；4)忽略弹丸对身管的摩擦及热效应；5)身管与周围环境只存在对流换热，忽略辐射传热；6)忽略身管附加件对传热的影响；7)环境气流与身管外表面各点的传热系数取相同值。

根据以上假设，身管传热问题得到了简化。根据传热学理论，可得到柱坐标系下不稳定一维径向传热问题的控制微分方程：

(1)

式中：t为时间；a为身管材料导温系数；r为身管内某点的半径，r0≤r≤R，其中r0、R分别为身管内外壁半径。

1.2 身管传热边界

身管传热边界是在身管与周围气流热交换过程的基础上确定的，内壁传热边界根据膛内火药燃气与膛壁强制对流过程进行确定，外壁传热边界根据外壁与环境气流的自然对流过程进行确定。

1.2.1 内壁传热边界

火药燃气在身管内为不稳定的湍流流动过程，假设高温燃气气流沿轴向平行入射到膛内，则沿轴向方向可分为热入口区和充分发展区2部分。由于燃气流体温度大于内膛表面的温度，因此会在热入口区形成热边界层；在热载荷的持续作用下，热边界层不断发展，最后达到热充分发展状态。身管中热边界层的发展如图2所示。

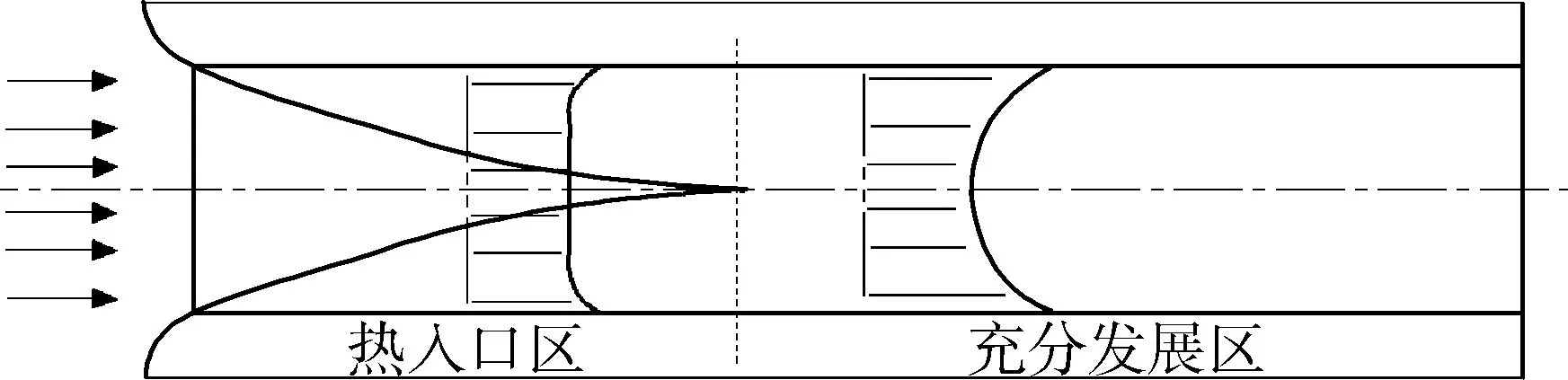
图2 身管中热边界层的发展

根据假设条件，忽略辐射传热的影响，得到内壁传热边界条件为

(2)

式中：λ为身管材料导热系数；Tg为膛壁燃气温度。

1.2.2 外壁传热边界

根据假设条件可知：身管外壁及射击间隔期的身管内壁通过自然对流的方式与环境气流进行热量交换。因此，身管外壁传热边界条件为

(3)

1.3 传热初始条件

火炮首发射击时，传热初始条件为射击前周围环境的温度，即T=T0；连发射击之后，传热初始条件发生变化，不再是周围环境的温度，而是前一发弹丸射击结束时的身管径向温度，即T=f(r)。

2 传热方程与传热简化模型

2.1 建立传热方程

膛内运动时期火药燃气的温度方程为

T=(fωψ-θφmv2/2)/(ωψR)，

(4)

后效时期火药燃气的温度方程为

T/T0=[1∓u(k-1)/(2c0)]2,

(5)

式中：f为火药力；ω为火药质量；ψ为火药已燃率；m为弹丸质量；v为弹丸速度；φ为次要功计算系数；θ=k-1，其中k为绝热指数；R为气体常数；u为火药气体速度；c0为未扰动区音速。

采用四阶龙格-库塔算法求解方程(4)、(5)，可得到2个时期火药燃气的温度分布规律。基于此，根据给定的初始条件及设定的身管传热边界求解传热控制方程，即可得到身管的传热分析结果。在设定身管传热边界时，h1是进行火炮身管温度场分析的前提，为此，根据马蒙托夫假定，建立内弹道时期身管膛壁对流换热系数的过程如下：

假定在其他参量不发生变化的条件下，质量为mq的火药燃气在与膛壁有热量交换的τ时间内与膛壁撞击所传递的热量为

Q=CV(T-Tw)mq,

(6)

式中：CV为火药气体的定容比热容。因此，可得到火药燃气与膛壁的热量传递速率为

Q/τ=CV(T-Tw)mq/τ,

(7)

又

mq=wr·F·ρ·τ，

(8)

式中：wr为火药燃气沿身管径向方向对膛壁的平均撞击速度；F为某一瞬时与火药燃气接触的膛壁面积；ρ为火药燃气密度。

因此，可得

Q/τ=CV ρwr(T-Tw)F，

(9)

可见：火药燃气在单位时间内传递给膛壁的热量与CV、ρ、wr、F及温差T-Tw成正比。结合牛顿冷却公式，可取h1=CV ρwr，于是式(9)可改写为

Q/τ=h1(T-Tw)F,

(10)

对于30mm自动炮，h1可简化为

(11)

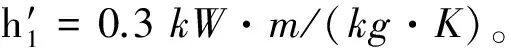
在射击间隔时期，膛内对流换热系数的计算采用与身管外壁相同的分析方法；在后效期阶段，膛内对流换热系数取弹丸内弹道结束时刻所对应的火药燃气的对流换热系数与射击间隔时期膛内对流换热系数的平均值。

2.2 求解传热方程

沿径向将身管及时间t进行离散化处理，采用有限差分方法求解内节点和边界节点的差分方程。

内节点温度方程：

Tj+1i′=F0[1+Δr/(2ri′)]Tji′+1+(1-2F0)Tji′+

F0[1-Δr/(2ri′)]Tji′-1。

(12)

式中：Δr为径向等分间隔；F0=aΔt/(Δr)2，为身管材料的傅里叶数,其中Δt为时间间隔；ri′为由内到外的第i′个节点半径；Tji′为第j个时间节点时位于第i′个径向节点处的温度。

膛壁温度方程：

2aΔtTj1/(Δr)2+[2aΔt/(Δr)2]×

(13)

外壁温度方程：

[2aΔt/(Δr)2]Tjm-1。

(14)

综上所述，身管热分析流程如图3所示。

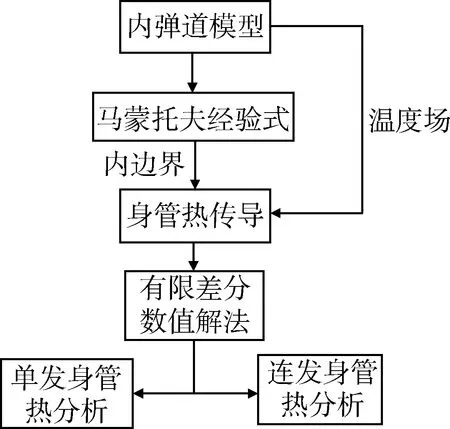
图3 身管热分析流程

2.3 传热简化模型

小口径火炮的射击规范要求每个点射5～7发，本文选取单点射7发进行连发射击时的热分析。此外，由于膛线起始部的膛压和温度都很高，换热也很剧烈，对内膛的烧蚀磨损作用最强，因此本文选取膛线起始部的结果进行分析。

为便于分析沿身管径向方向的温度场分布情况，在膛线起始截面上对身管沿径向取A、B、C、D、E五个节点,其中：A在身管膛壁上；B在铬层与钢基体的交界面上，距内壁0.05mm；E在身管外壁上，距内壁19.5mm；C和D为B和E之间的点，分别距膛壁6.83mm和13.17mm。身管径向节点分布如图4所示。身管热分析时的初始参数如表1所示。

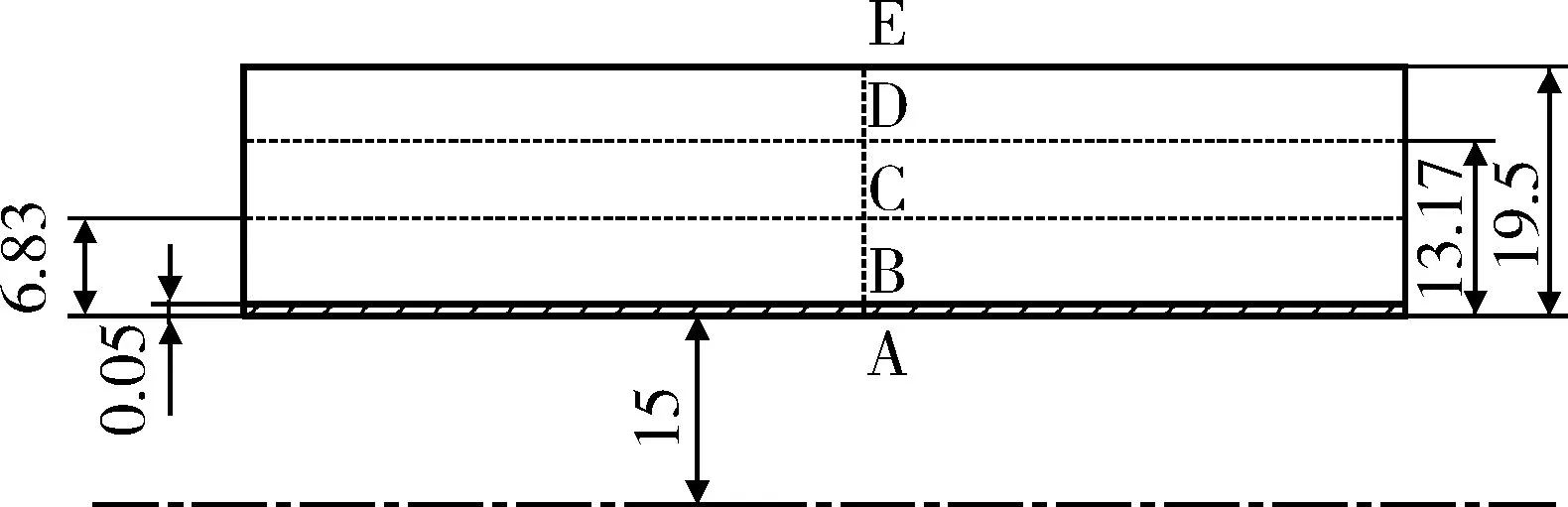
图4 身管径向节点分布

表1 身管热分析时的初始参数

3 身管温度场数值模拟

3.1 单发射击温度场

单发射击身管温度分布三维图及膛壁温度变化规律如图5所示。可以看出：在火药燃气高的对流换热系数与温度的综合影响下，身管从火药燃气中获得的热量很多，使得膛壁在极短时间内达到高温，身管内壁在极短时间内上升到最高温度，接近1 200K。

单发射击膛壁温度最大时刻身管温度沿径向分布如图6所示。可以看出：在膛壁温度最大时刻，膛壁从火药燃气中获得的热量聚集在内膛表面，而在身管传导热阻的影响下，热量不能及时沿径向传导，使得沿径向方向产生很大温度梯度，仅在距膛壁2.5mm(对应r=17.5mm)左右降至环境温度。

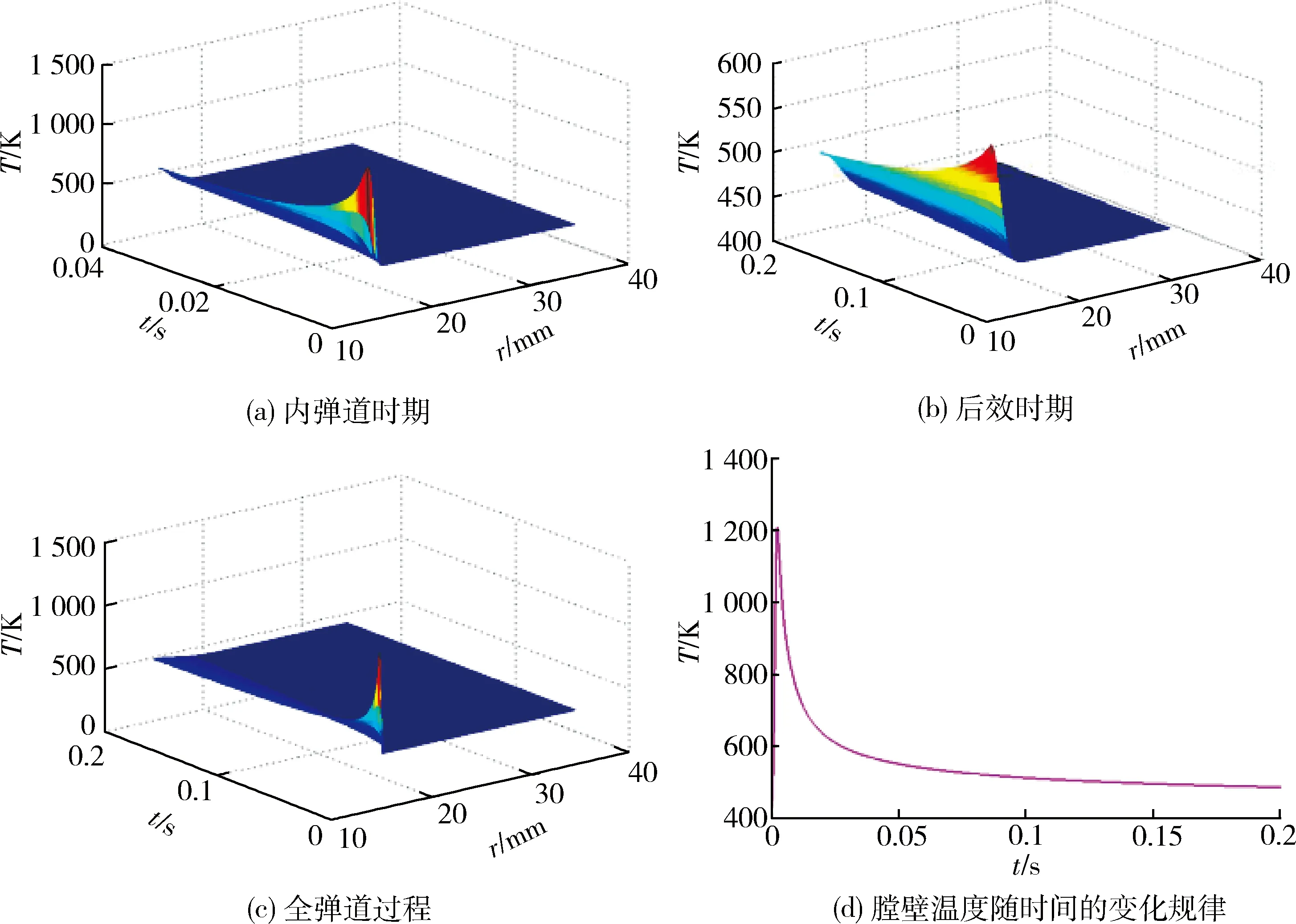
图5 单发射击身管温度分布三维图及膛壁温度变化规律

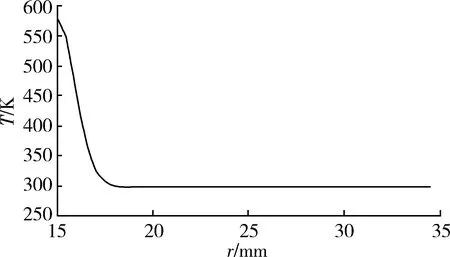
图6 单发射击膛壁温度最大时刻身管温度沿径向分布

3.2 连发射击温度场

30mm小口径自动炮的战技指标规定射速不低于300发/min，即0.2s/发。图7为连发射击时身管温度变化三维图，图8为连发射击时身管内壁及铬层交界面温度变化，图9为连发射击径向各点(B、C、D、E)的温度变化规律。

由图7、8可知：连发射击时身管内壁的温度呈现周期性的升降，每发射击时内壁温度变化形式与单发射击时基本相同，由于射击间隔时间很短，热量不能及时传递出去，在连发射击过程中逐渐累积，使膛壁峰值温度逐发上升，同时射击间隔期回落的最低温度也相应升高。由图9可知：一方面，身管内的节点B也呈现相同的温度分布规律，其波动幅度较内壁小，节点C、D、E温度也呈现逐发上升的趋势，但由于距内壁较远，温度的脉冲特性不明显，基本呈线性的平缓增长趋势；另一方面，随着射弹量的增加，身管各节点的峰值温度和回落最低温度的增加幅度都逐渐减小，随着热量逐渐向外传递，节点C、D、E温度也相应增加，使得身管内、外壁的温差逐渐降低。此外，由图8可知：铬层交界面与身管内壁相比，除上升阶段的峰值较小外，二者回落阶段的变化趋势基本一致。

图10为不同时刻身管温度沿径向的分布，各条曲线分别对应第1、3、5、7发射击后效期结束的时刻。可以看出：不同时刻沿身管内壁的温度分布呈现相同的形式，受身管热阻的影响，聚集在内壁表面的热量由内至外缓慢渗透，节点对温度的敏感性随半径增大而逐渐减弱，表现为内节点的温度变化缓慢，温升幅度较小；由于铬层很薄，仅有50μm，且铬材料的热传导率比身管材料高，因此在铬层与钢基体交界面附近温度梯度不明显。

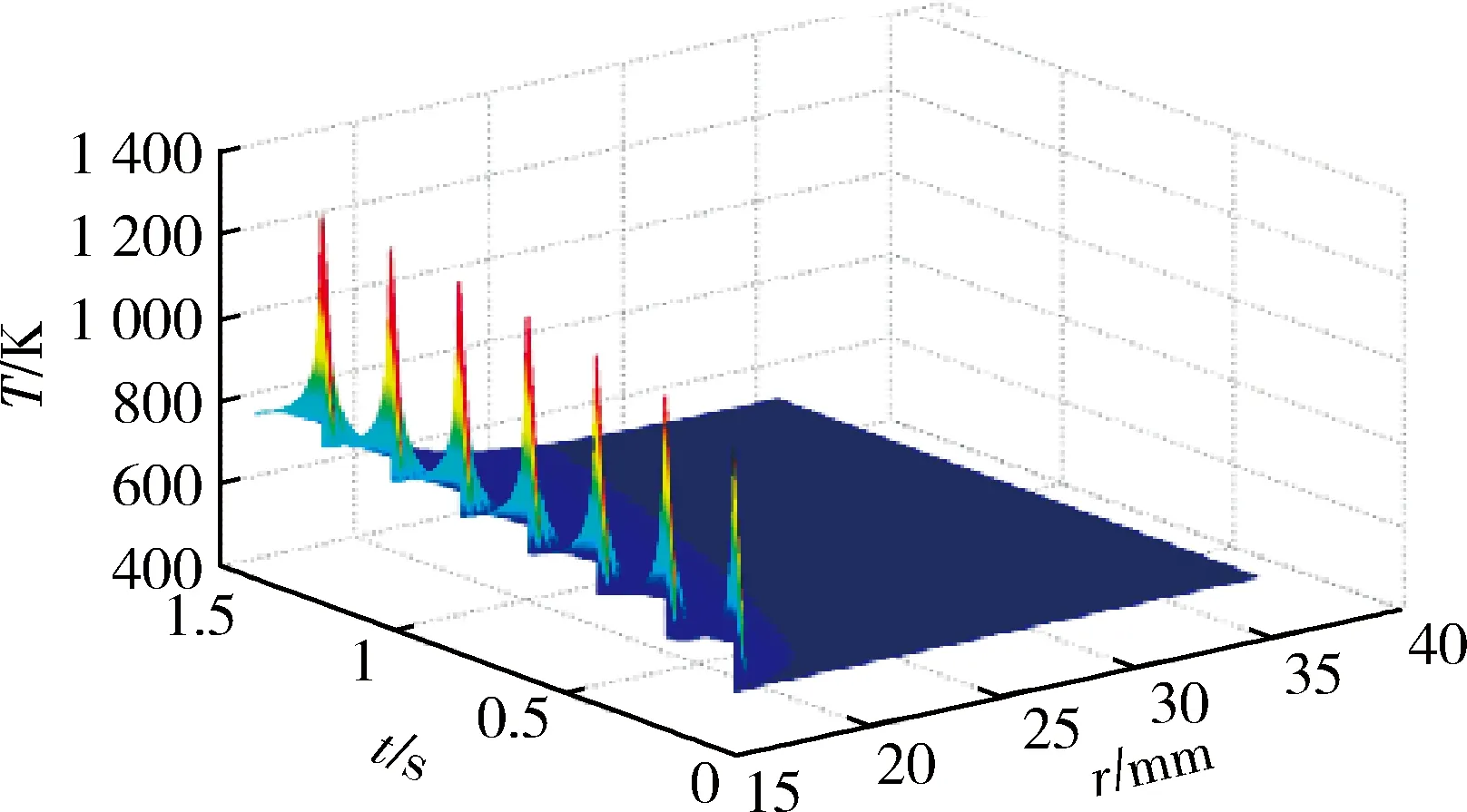
图7 连发射击时身管温度变化三维图

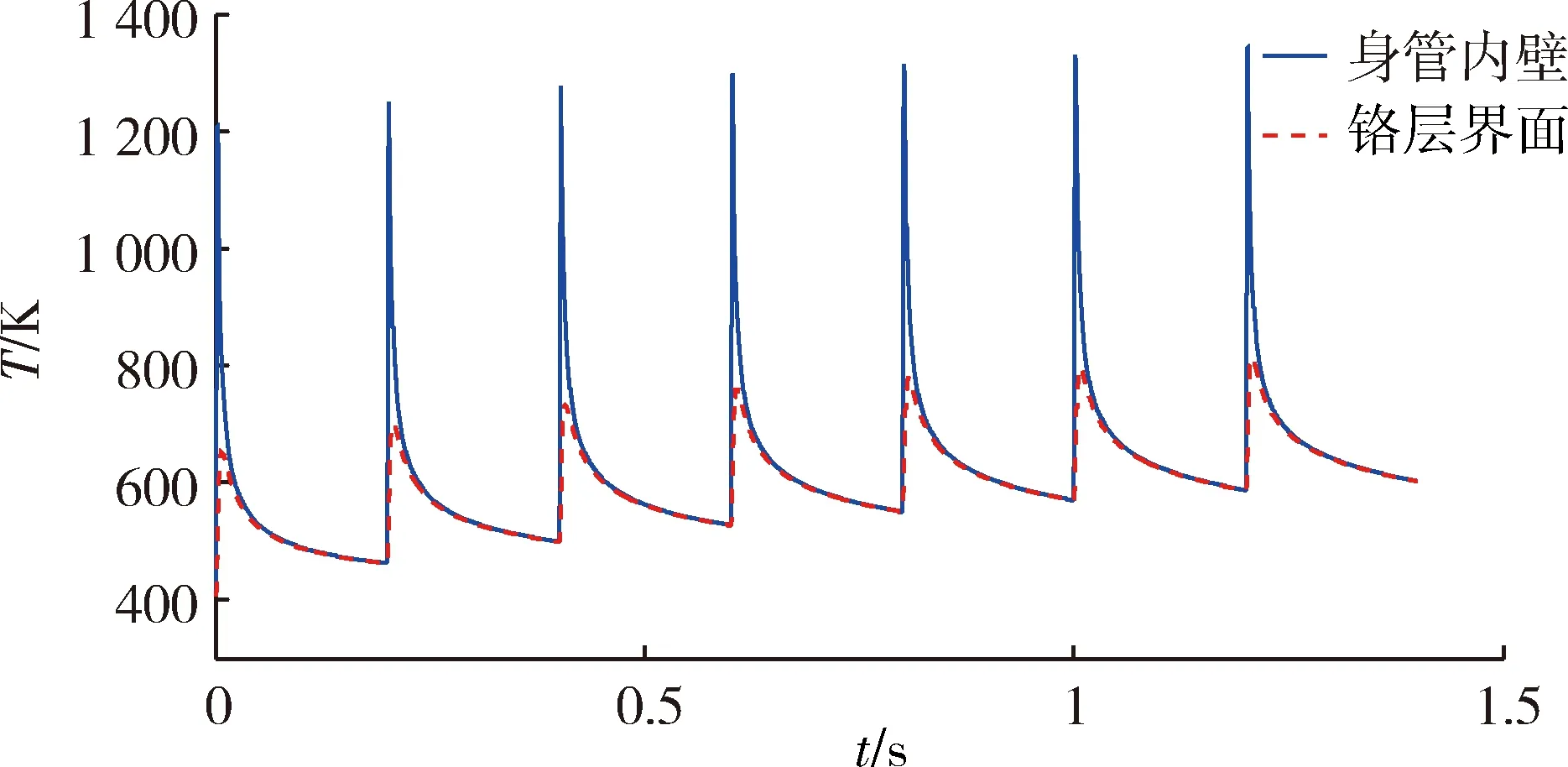
图8 连发射击时身管内壁及铬层交界面温度变化

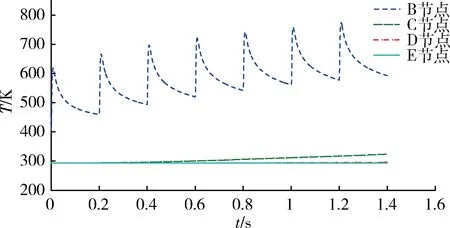
图9 连发射击径向各点温度变化规律

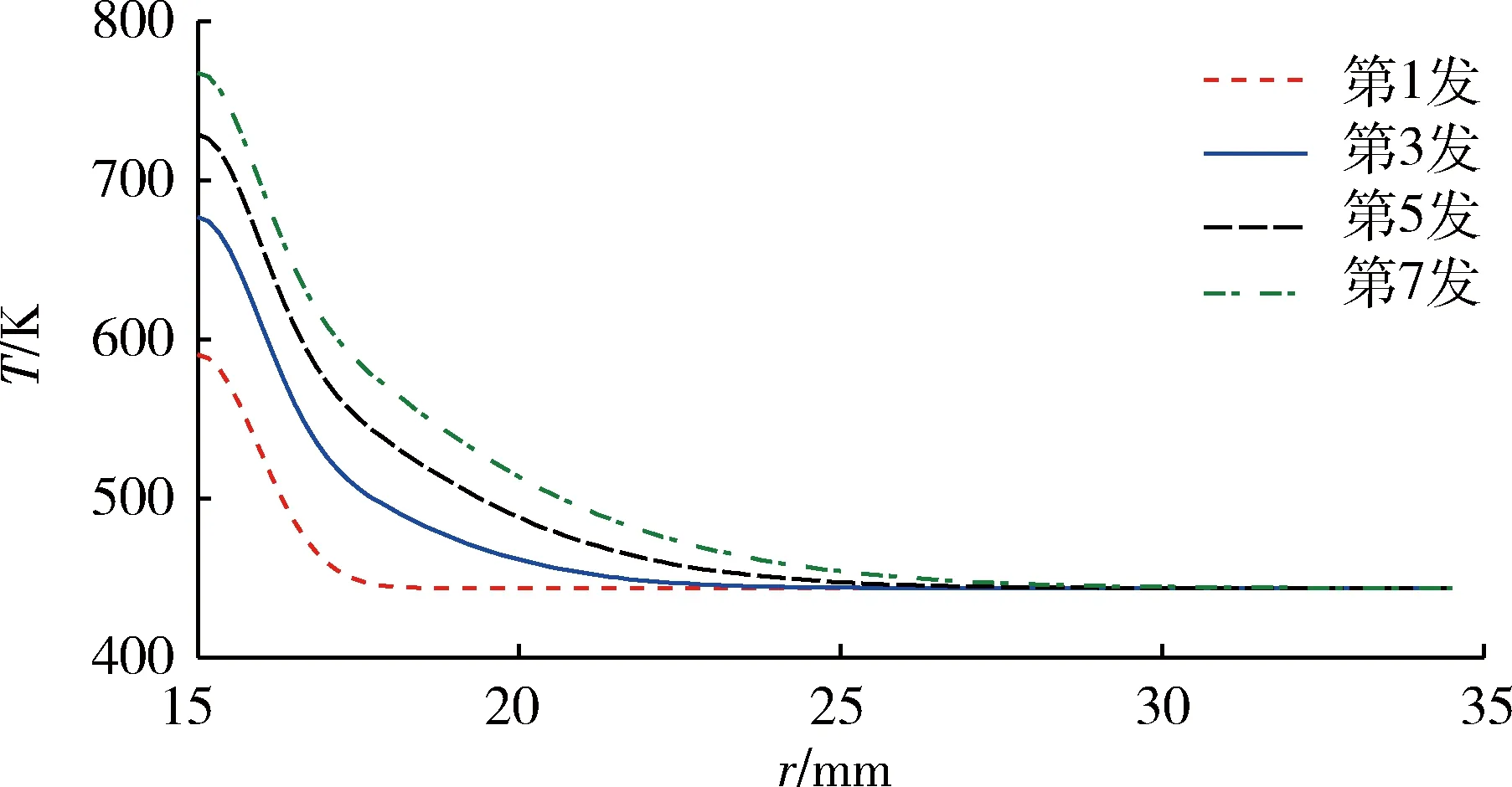
图10 不同时刻身管温度沿径向分布

4 结论

以30mm小口径火炮身管为例，分析了单发及连发射击条件下温度场分布及其变化规律，研究结果为分析内膛烧蚀机理、计算烧蚀磨损量，进而预测身管寿命奠定了基础。下一步将在此基础上，研究内膛烧蚀磨损量与膛壁温度的相关关系，并计算单发及连发射击条件下内膛的烧蚀磨损量。

[1] 谈乐斌，张相炎，管红根.火炮概论[M].北京：北京理工大学出版社，2014:40-45.

[2] 吴斌,夏伟,汤勇.射击过程中热影响及身管热控制措施综述[J].兵工学报,2003,24(4):525-529.

[3] 武锋,郑祖华,吴圣川.大口径火炮多发连射身管热力耦合分析[J].中国机械工程,2012,23(9):1056-1059.

[4] 杨艳峰,郑坚,狄长春，等.基于ANSYS火炮身管传热仿真[J].火力与指挥控制,2013,38(8):134-136,140.

[5]Gao R P,Ye S.Improved Adaptive Pruning Algorithm for Least Squares Support Vector Regression[J].Systems Engineering and Electronics,2012,23(3):438-444.

[6]Chen M M.Projectile Balloting Attributable to Gun Tube Curvature[J].Shock and Vibration,2010,17(1):39-53.

[7] 孔国杰,张培林,钱林方.一种新的火炮剩余寿命评定方法[J].弹道学报,2010,22(3):21-25.

[8] 陈永才,宋道志.国内外火炮身管延寿技术研究进展[J].兵工学报,2006,27(2):330-334.

[9] 张国平,王茂林,杨东.某火炮身管寿命问题探讨[J].火炮发射与控制学报,2013(3):1-5.

[10] 林少森,闰军,俞卫博,等.身管烧蚀及缓蚀剂作用机理研究现状[J].火炮发射与控制学报,2016(1): 92-96.

[11] 李明涛,崔万善,姚哲.基于内表面熔化层理论的身管寿命预测方法[J].火炮发射与控制学报,2009(2):5-8.

[12] 孟翔飞.武器身管寿命预测模型及内膛参数综合检测系统研究[D].南京:南京理工大学,2013.

[13] 朱文芳，王育维，魏建国，等.某火炮多发连续射击炮管传热计算分析[J].火炮发射与控制学报，2010(6):74-78.

[14] 欧阳青.火炮身管烧蚀磨损与寿命问题研究[D].南京:南京理工大学,2013.

(责任编辑:尚彩娟)

Numerical Simulation of Heat Transfer and Temperature Distribution of Artillery Barrel

XU Da, LUO Ye, FAN Wen-bo

(Department of Arms Engineering, Academy of Armored Force Engineering, Beijing 100072, China)

To study the temperature distribution characteristics of small caliber barrel under different shooting conditions, firstly, the propellant gas temperature equations during the interior ballistic period and the aftereffect period are established, the initial conditions of heat transfer are determined; then the heat transfer coefficient of bore-surface during the interior ballistic period is analyzed, and heat transfer boundary is clarified; after that, the heat transfer model of artillery barrel is established based on the theory of heat transfer, and the model is resolved by the finite difference method; finally, taking the 30 mm barrel with chrome plating as an example, the temperature field distribution and variation law under the single and repeating firing conditions are analyzed, and the conclusion is drawn that the temperature gradient near the chromium layer is not notable, which lays the foundation for the future research on the life of small caliber barrel.

artillery barrel; heat transfer; numerical simulation; temperature distribution; chromium layer

2016-07-14

军队科研计划项目

徐 达(1969-)，男，教授，博士。

TJ012.1+3

：ADOI：10.3969/j.issn.1672-1497.2016.06.010

1672-1497(2016)06-0050-05