基于概率盒理论的滚动轴承故障信号建模方法

杜 奕， 丁家满， 刘力强

(1.昆明理工大学 城市学院，昆明 650051； 2. 昆明理工大学 信息工程与自动化学院，昆明 650500)



基于概率盒理论的滚动轴承故障信号建模方法

杜 奕1， 丁家满2， 刘力强1

(1.昆明理工大学 城市学院，昆明 650051； 2. 昆明理工大学 信息工程与自动化学院，昆明 650500)

为了解决机械故障诊断存在特征提取带来的信息丢失问题和多段平均丢弃数据不确定性的问题，提出了一种基于概率盒理论的机械故障信号建模方法。以滚动轴承故障信号为研究对象，分析原始信号的概率分布类型，获得概率分布类型参数的不确定性区间，提出基于确定概率分布类型的概率盒建模方法。针对故障信号概率分布类型难确定问题，提取原始信号的特征，利用特征信号的有序性，提出基于特征提取的概率盒建模方法，以歪度和峭度特征为例，对比两种特征概率盒的异同点。基于概率盒定义，将原始数据的不确定性直接映射到概率盒的上下界，提出无需验证数据概率分布类型的原始数据概率盒直接建模方法。通过滚动轴承实测数据，对比三种方法的有效性及适用性，与传统特征提取方法对比，证明了方法的有效性。

滚动轴承；故障诊断；不确定性；概率盒理论；DS结构体

机械故障诊断的一个关键步骤是对采集到的数据进行特征提取，再对特征进行分析与处理，以实现故障诊断与模式识别。赵志宏等[1]提出一种基于多小波系数的机械故障特征提取方法，对机械振动信号提取了多小波系数的最大值、最小值、均值等统计特征。向丹等[2]提取了振动信号的EMD能量熵和EMD奇异熵作为时频分布统计特征进行了设备的故障诊断。任立通等3]提出基于随机共振预处理的故障特征提取方法，分别提取基于时域、频域及时频域分析的故障特征集用于故障诊断。唐贵基等[4]利用局部均值分解算法对故障信号进行自适应分解，利用峭度准则及切片双谱分析，提取了故障特征频率信息。隋文涛[5]提出一种基于平稳小波变换的降噪方法以提取不同尺度上故障信号的小波分解系数的峭度特征。对原始信号的特征提取能将故障信息凸显出来，但也这不可避免带来两个问题：① 对原始信号的特征提取带来特征之外信息的丢失；② 多段平均的结果忽略了多段信号带来的采样不确定性和信号随时间而变化的波动量。

本文将概率盒理论(probability boxes，p-boxes)引入到机械故障诊断中，以解决上述两个问题。p-boxes思想的提出最初在于用“区间”表达纯粹“认知不确定性”，经历过与模糊理论[6]、DS证据理论[7]、基于传统概率论的布尔逻辑推理[8]、稀疏样本的Kolmogorov方法[9]等的交叉研究，其理论既融入了贝叶斯推理、证据理论等随机类算法，同时也融入了如神经网络[10]、专家系统、模糊集理论[11]等人工智能算法。随着2003年美国Sandia国家实验室与美国能源部合作的不确定性研究报告[12]的发布，概率盒在理论方面进入一个相对成熟的阶段。概率盒理论的应用先后涉及到故障系统失效概率评估[13]、振动系统动态响应不确定性评估[14]、缺乏实验数据条件下的汽车变速箱可靠性设计[15]、火箭边缘外壳结构有限元建模及参数优化[16]、阻尼振荡器中多参数不确定性关联[17]、机械可靠性系统架构与评估[18]、测量系统的误差累计表达与评估[19]、考虑气候变化下的百年后海平面估计[20]等。因为其在不确定性问题的表达与处理方面的巨大优势，概率盒理论的研究及应用领域也在不断扩大。

本文以滚动轴承故障信号为具体研究对象，提出一种基于概率盒理论的机械故障信号建模方法。利用对原始数据的概率盒建模来避免因特征提取带来的信息丢失，利用概率盒的内外包络功能来避免因多段平均处理而忽略掉的不确定性信息。在分析采样数据的概率分布类型基础上，提出基于概率分布类型的参数估计概率盒建模方法。针对原始信号难确定概率分布类型的问题，提出基于故障特征的概率盒建模方法和完全无需对原始数据进行概率分布类型确定的原始数据概率盒直接建模方法。后者提高了建模方法的适用性，并具有向其他故障建模推广的能力。最后与传统的特征提取方法对比证明了建模方法的有效性。

1 概率盒及DS结构体

1.1 概率盒(p-boxes)的描述

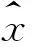
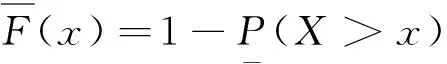
(1)

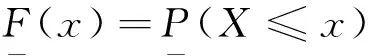
(2)

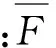
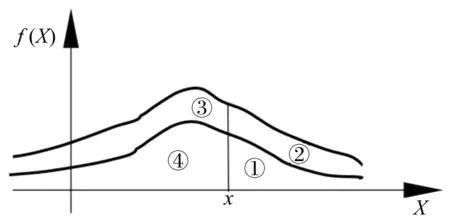
图1 p-box定义示意图Fig.1 Schematic diagram of p-box definition

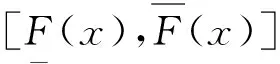
(3)

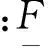
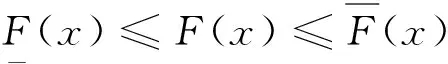
(4)

1.2 DS结构体(DSS)的描述

DS证据理论在概率盒理论的发展中起到了至关重要的影响，p-boxes的重要组成单元是DS结构体(Dempster Shafer Structure，DSS)。P-boxes和DS理论都包含以下基本概念：

1) 基本概率分配(Basic Probability Assignment，BPA)，用mass函数表达，简称为m函数，也称为概率片。mass函数满足以下条件：

m(Ø)=0

(5)

m(ai)=pi

(6)

式中:pi>0，且∑pi=1，i=1,2,...,n。

2) 置信函数和似然函数。

置信函数Bel：将所有集合b⊂R的子集ai的概率片值累加的结果。

(7)

似然函数Pls：将所有与集合b⊂R有交集的子集ai的概率片值累加的结果。

(8)

置信函数和似然函数满足以下条件：

Bel(b)≤Pls(b)

(9)

与DS理论不同的是，DSS的焦元不再是某个假设事件，而是具体到一个带有不确定性的闭区间。这种特殊化的处理简化了DS证据理论的公式，并由此得到了DS结构体(DSS)。具体定义如下：DSS是由多个焦元组成的集合，其中每个焦元包含一个闭区间及发生在该闭区间的BPA。DSS表达式为：{([x1,y1],m1),([x2,y2],m2),…,([xn,yn],mn),}

其中，每个焦元([xi,yi],mi)满足以下条件：

xi≤yi

(10)

∑mi=1

(11)

式中:i=1,2,…,n，如果存在xi=xj，应确保yi≠yj。

DSS对DS证据理论的特殊化处理使其适用范围由对事件发生的假设决策处理转移到对原始数据的不确定性问题的区间表达，从信息融合的三层架构(数据层、特征层及决策层)角度分析，DSS更偏向于数据层的处理，并在原始数据的不确定性表达方面体现出强大的优势。

1.3 P-boxes与DSS的关系

P-boxes与DSS之间可以相互转化，但彼此间不是一一对应的映射关系。多个满足一定相同条件的DSS可以映射到同一个p-box，这意味着DSS向p-box转化中存在着信息丢失；同一个p-box在不同条件下也可以转化为不同重采样率的DSS。

假设某个DSS定义如下：

{([x1,y1],m1),([x2,y2],m2),…,([xn,yn],mn),}

将该DSS转化为p-box的过程表达如下：

鄂麦398系是湖北省农业科学院粮食作物研究所从杂交组合皖1216/25871//扬麦 13经10年10个世代系谱法选育而成的高产多抗小麦新品种。

(12)

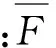
(13)

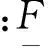
P-boxes和DSS总体可以理解为整体与局部的关系。如图2所示，每两条灰色细水平线间所夹的子空间对应于DSS的某个焦元([xi,yi],mi)，子空间的水平方向对应[xi,yi] ，高度对应mi，子空间累加后得到的左右边界分别对应于p-box的上下边界。

黑色粗直线包含的就是概率盒，两灰色细直线包含的矩形即是DSS的焦元，横坐标表示区间，矩形的高表示焦元的mass值。

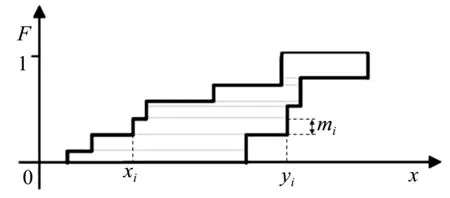
图2 DSS转化为p-box示意Fig.2 Schematic diagram of DSS into p-box

当p-box由两条连续的CDF组成时，为了实现对p-box的卷积运算，需要对其离散化，以得到不同采样频率下的DSS。如图3所示。

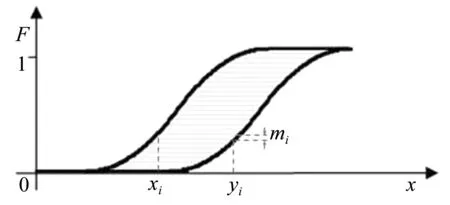
图3 p-box转化为DSS示意Fig.3 Schematic diagram of p-box into DSS

已知构成p-box的两条CDF，通过等信度离散化得到由多条细线组成的DSS，表示如下：

{([x1,y1],m1),([x2,y2],m2),…,([xn,yn],mn),}

式中:：m1=m2=…=mn=1/n，n为重采样率。

2 振动信号的提取

图4 实验装置实拍图Fig.4 Picture of experimental apparatus

实验轴承为NU205圆柱滚子轴承，在外圈和内圈上分别切割出长宽深为15 mm×0.5 mm×0.5 mm的线割槽，用来模拟外圈、内圈局部损伤故障；在其中一个滚动体上切割出宽深为0.5 mm×0.5 mm的线割槽，用来模拟滚动体局部损伤故障，故障轴承实体如图5所示。

图5 故障轴承实体图Fig.5 Pictures of fault bearings

电机转速为800 r/min，采样频率为10 240 Hz，由理论公式得到的滚动轴承故障特征频率如表1所示。

表1 滚动轴承故障特征频率( Hz)

实验轴承加速度信号的时域波形和功率谱如图6所示。

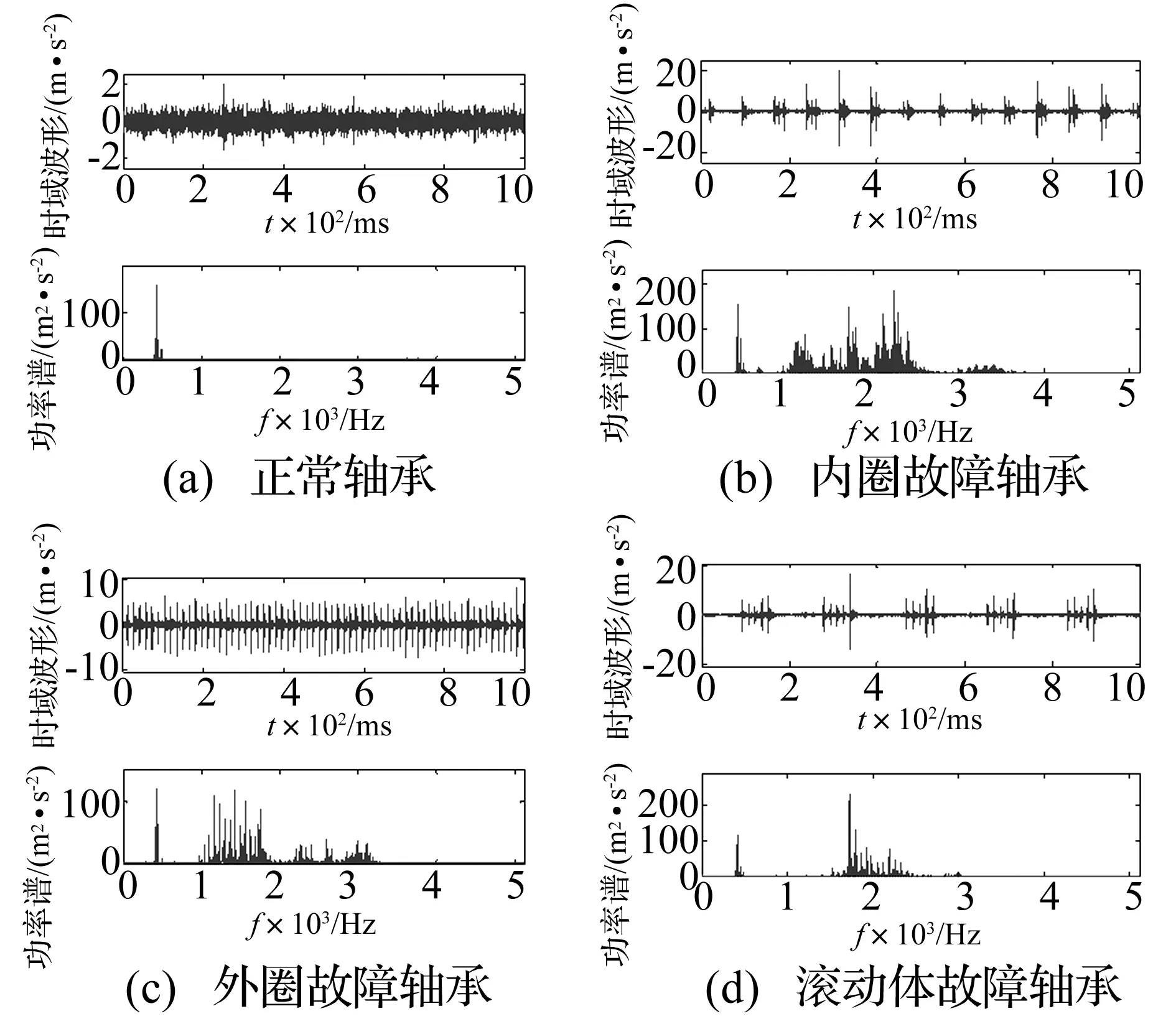
图6 实验轴承加速度信号的时域波形和功率谱Fig.6 Time domain waveform and power spectrum of experimental bearing acceleration signals

3 故障信号的概率盒建模方法

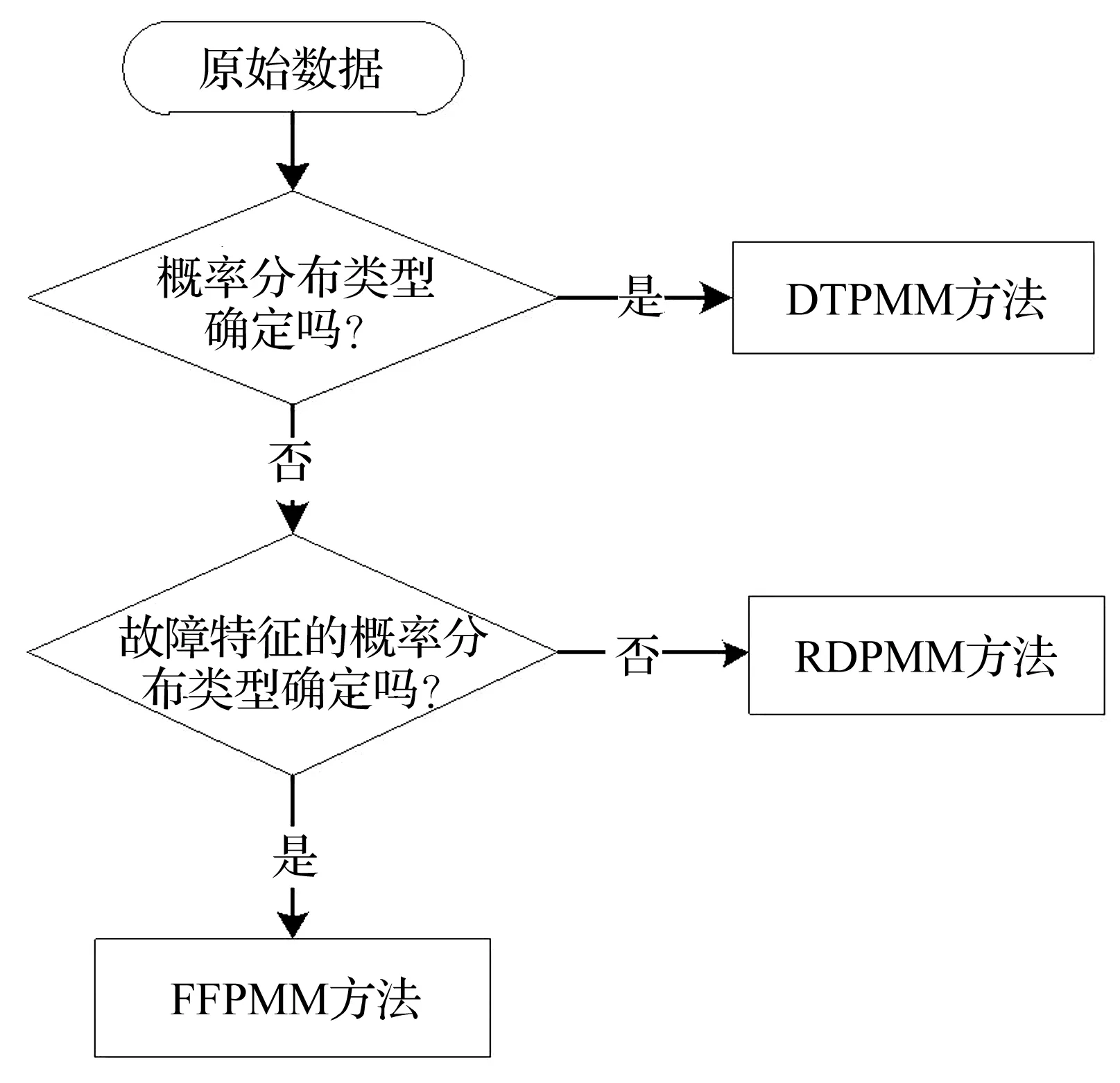
图7 本文三种建模方法的关系Fig.7 Relationship among modeling methods

概率盒建模方法有：专家估计方法、卷积建模方法、鲁棒贝叶斯方法、约束规范方法和实验测量方法等[1]。所有概率盒建模方法都应具有一个共同属性，即需要将不确定数限制在概率盒内，并在有限信息量的前提下达到最优，并都能体现出样本不确定性。每种建模方法都有其适用范围及优势和缺陷。单独的应用某种方法并不能解决滚动轴承故障信号具体问题。笔者在分析对比了不同轴承故障的概率特性的基础上，分别提出三种概率盒建模方法。关系如图7所示。当采集的原始数据服从某种概率分布类型时，采用基于概率分布类型的概率盒建模方法(The p-boxes modeling method based on distribution type，DTPMM)。当出现机械故障时，采集的故障信号可能不满足现有的任何概率分布类型时，DTPMM不再适用。为此本文提出故障轴承的特征概率盒建模方法(The p-boxes modeling method based on fault feature，FFPMM)。当故障特征的概率分布类型无法确定时，FFPMM不再适用。本文提出实验数据概率盒直接建模方法(The p-boxes modeling method based on raw data，RDPMM)。RDPMM方法因为无需对验证数据的概率分布类型，因此适用范围更广。

3.1 DTPMM建模方法

DTPMM建模方法基本思路如下：分析实验采集的原始数据，判断数据集服从哪一种概率分布类型，如：正态分布对应的是均值参数μ和方差参数σ，指数分布对应的是指数参数λ等。分别获取这些参数的不确定性区间，建立单一DSS，选择离散率，实现DSS的离散化，带入概率分布函数CDF，获取p-boxes。

以原始数据服从正态分布为例，获得概率盒的建模算法描述如下：根据采样频率将数据分为若干组，每组数据包含10 240个数据；获得每组数据的均值和方差；获得均值的DSS，形式为[μmin，μmax，1]，其中μmin和μmax分别表示均值的最小值和最大值；获得方差的DSS，形式为[σmin，σmax，1]；对DSS进行离散化；将离散化的DSS上界和下界分别累和得到概率盒的上界和下界。

3.2 FFPMM建模方法

当出现故障时，采集的原始信号的概率统计特性趋于复杂，甚至有可能不再服从现有的任何概率分布类型，上述DTPMM建模方法不再适用。对原始信号的故障特征提取虽然会导致特征意外信息的部分丢失，但故障特征能更加直观的反映故障本质，是对原始信号的弥补与支撑。为此，本文提出一种基于特征提取的概率盒建模方法。在特征选择方面，与有量纲特征相比，无量纲特征更能满足提取特征的“快速反映状态变化”和“对机器工况不敏感”的特性。歪度和峭度分别对应着随机变量的三阶矩和四阶矩：

歪度：

(14)

峭度：

(15)

采用歪度和峭度为概率盒的特征，建立故障特征概率盒有利于对比两者间的异同点。歪度特征的概率盒建模的具体算法描述如下：根据采样频率将数据分为若干组，每组数据包含10 240个数据；获得每组数据的歪度；对歪度数据进行正态分布概率类型验证；确定歪度数据的均值和方差的DSS；对DSS进行离散化；将离散化的DSS上界和下界分别累和得到概率盒的上界和下界。峭度概率盒建模算法类似。FFPMM算法充分利用了DTPMM算法的建模思路，不同的是概率分布类型的验证对象不是原始测量数据，而是对原始数据特征提取后的特征数据。

3.3 RDPMM建模方法

从原始数据可以提取丰富的各类特征，每种特征建立的概率盒从形式和紧致性上比较也各不相同，这为概率盒的融合提供了大量的融合源。但与此同时也带来了两个问题。

(1) 必须验证特征数据是否服从某一特定的概率分布类型，如果无法找到其服从现有的任何一种概率分布类型，则需找到其他解决方法。

(2) 特征提取就意味着放弃了原始数据的其他丰富的概率统计信息。

为此，本文在概率盒的实验测量建模方法[7]的基础上，从概率盒的定义出发，提出一种直接从实验原始数据中建立概率盒的方法，该方法避免了特征提取，也避免了对原始数据的概率分布类型的检验。RDPMM建模方法的具体算法表述如下：将原始数据按采样频率转化为m行n列的数组，其中m为采样次数，n为采样频率，截除多余数据；将每次采样数据按从小到大的次序排列，得到新的数组；从m次采样数据中找到每列中的最小值和最大值，分别得到一个最小值和最大值的行向量；分别累加最小值行向量和最大值行向量得到概率盒的下界和上界。

4 实验结果与分析

以第2部分的实验数据为例验证以上三种概率盒建模方法。通常，多数故障发生的概率服从威布尔分布、对数正态分布、指数分布等典型分布类型，但实验采集的是振动加速度振幅信号而非故障发生的概率。图8(a)是对正常轴承采集信号的正态分布验证结果，定性观察其基本服从正态分布，并通过Kolmogorov-Smirnov 正态性检验方法得到样本集与标准正态分布比对结果吻合度为91.23%。

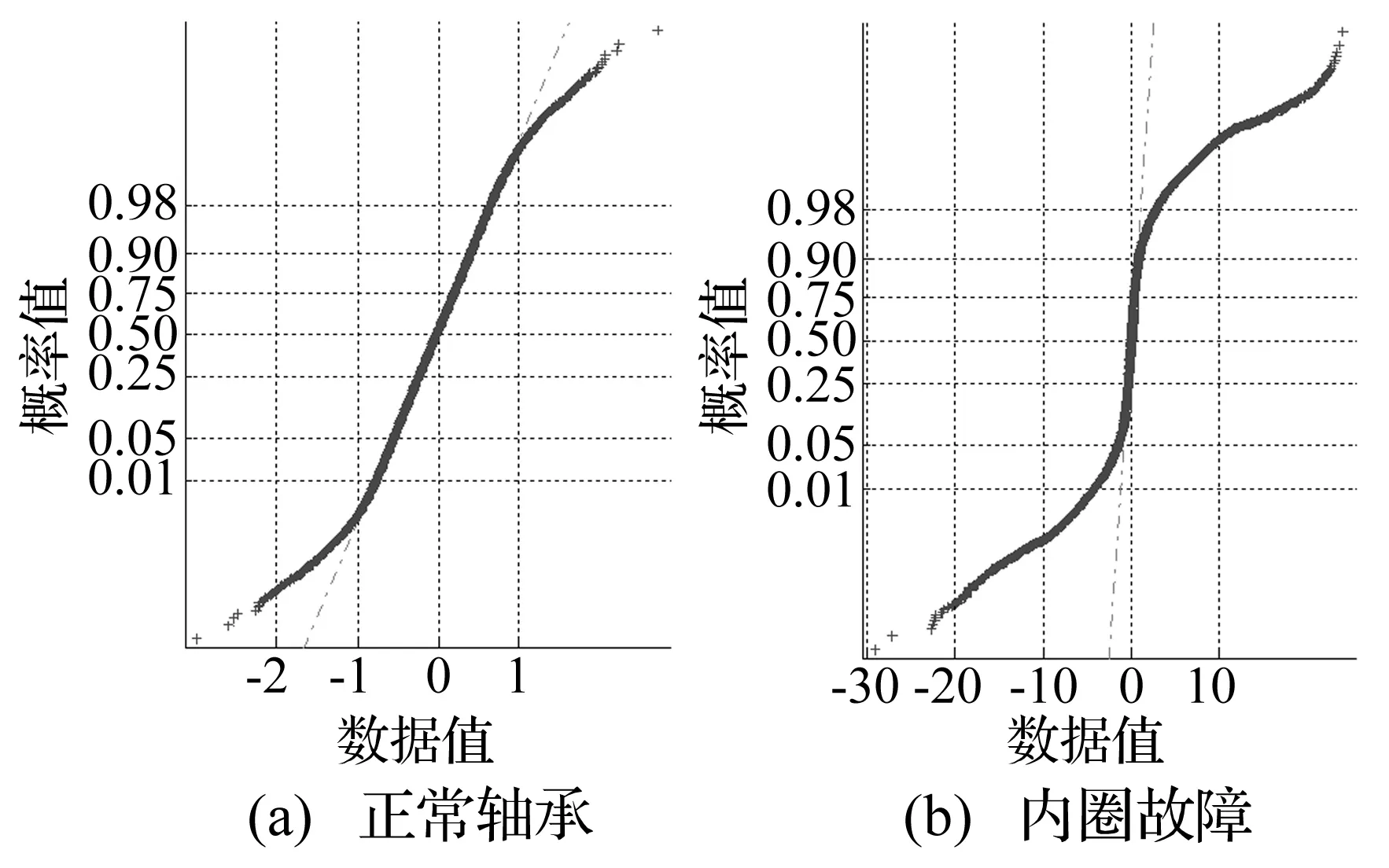
图8 实验数据的正态分布验证结果Fig.8 Normal distribution Verification results of experiment data

利用DDPMM建模方法得到的正常轴承概率盒结果如图9所示。与传统的Monte Carlo方法形成单一CDF不同，数据的不确定性被包含在p-box中。

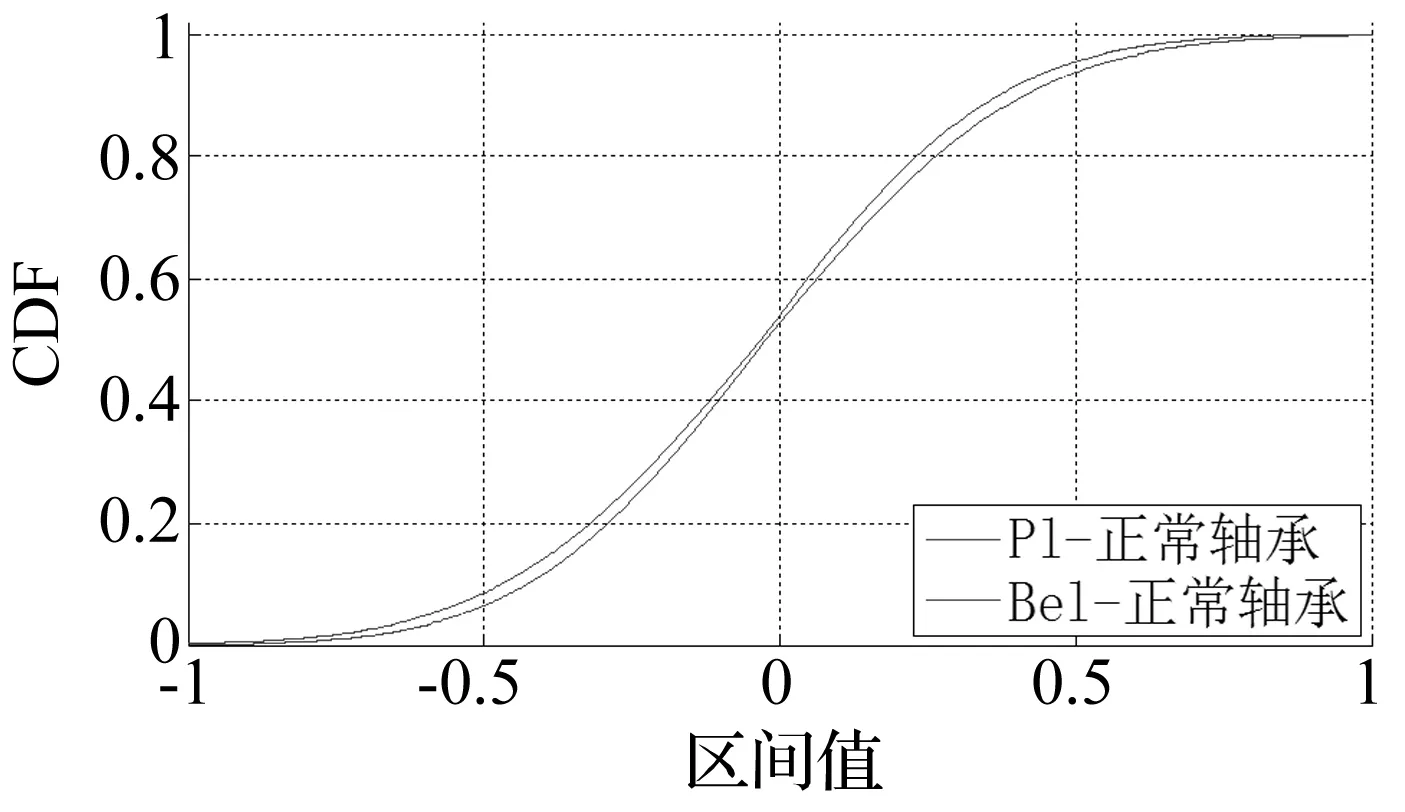
图9 正常轴承的正态分布概率盒结果Fig.9 Normal distribution p-boxes of normal bearing

对内圈故障、外圈故障及滚动体故障信号进行概率分布类型验证，结果发现，其既不服从正态分布类型，也不服从现有的任何一种概率分布类型，因此DDPMM建模方法不再适用。

图10给出的是内圈故障轴承的歪度数据的正态分布验证，基本服从正态分布。利用Kolmogorov-Smirnov 正态性检验方法进行定量验证的吻合度结果为89.87%。与图7(a)相比，吻合度略有下降，这是由于特征提取带来的特征样本数的骤减，随着原始采样数据量的增加是可以改善的。本文也对其他故障信号的歪度和峭度数据做了正态分布验证，结果类似。

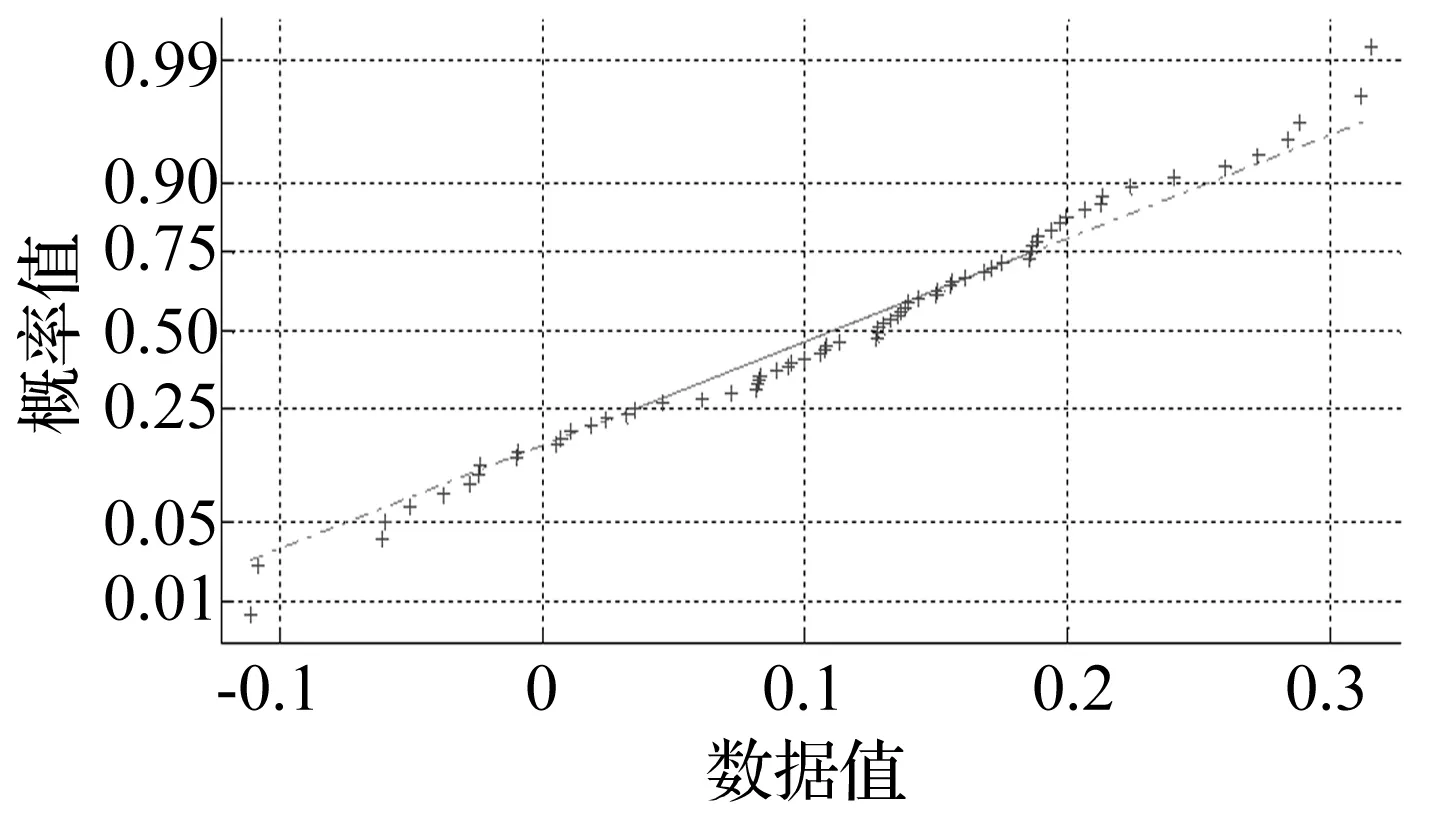
图10 歪度数据的正态分布验证结果Fig.10 Normal distribution p-boxes of skewness data

根据FFPMM算法得到的四种不同轴承加速度信号的歪度特征概率盒结果如图11所示。图中，横坐标表示概率分布的分位点，纵坐标表示累积概率分布。“PL”和“Bel”分别表示概率盒的置信上界和下界。为了数据显示的清晰，概率盒在横坐标上截去了[-1,1]以外的数据。实线、短虚线、点划线和长虚线分别代表正常、内圈故障、外圈故障和滚动体故障概率盒。

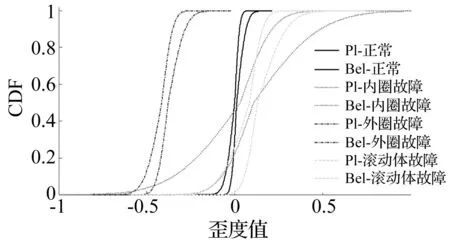
图11 歪度特征概率盒结果Fig.11 P-box results of skewness characteristics

峭度特征概率盒如图12所示。为了数据显示的清晰，在X轴方向截去了[0,80]以外的数据。

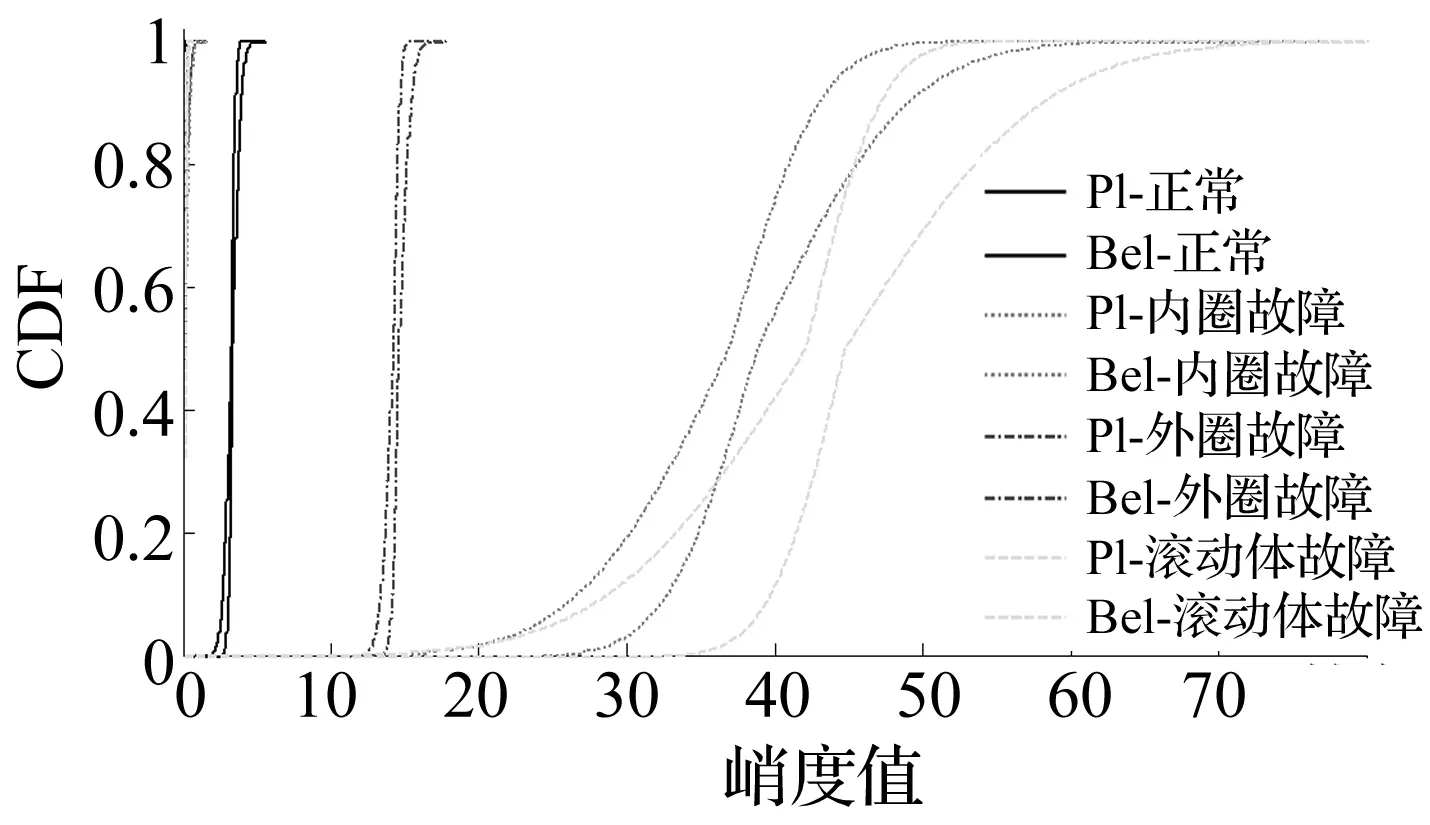
图12 峭度特征概率盒结果Fig.12 P-box results of kurtosis characteristics

对比图11和图12可以得到峭度和歪度概率盒的异同点，结论如下：歪度概率盒的紧致性较峭度概率盒强，即随着随机变量的概率统计阶矩的增加，概率盒区间包含的不确定也在增加。峭度概率盒的重叠程度没有歪度概率盒的大，更有利于模式识别。对比峭度概率盒和歪度概率盒，可以看出各有优缺点，这也为滚动轴承概率盒的特征选择提供了指导原则。

根据RDPMM算法，得到的四种不同轴承加速度信号的原始数据概率盒直接建模结果如图13所示。

图13 实验数据概率盒直接建模结果Fig.13 Direct p-box modeling results of experimental data

分析该图可以得到以下几点结论：

(1) 用实验数据直接建模得到的概率盒的边界是最窄的，即紧致性最高。这是因为从原始数据直接建模的过程不存在特征提取过程就不存在原始数据信息丢失问题，但也正是因为这个原因导致了处理数据量的增加，需要付出更多的运算成本和时间。

(2) 四种不同故障状态下的轴承概率盒之间几乎没有重叠现象，这一点也归功于概率盒紧致性的提高。与正态分布概率盒结果，峭度、歪度概率盒结果相比，RDPMM建模方法是最有利于模式识别的。

以正常轴承的拾取信号为例，表2给出四种不同建模方法的定量描述。其中y1和y2分别从不同的角度表达概率盒的累积统计量，累积统计量表达了概率盒的紧致性，该值越小，表示概率盒所包含的不确定区间越小，公式如下：

(16)

(17)

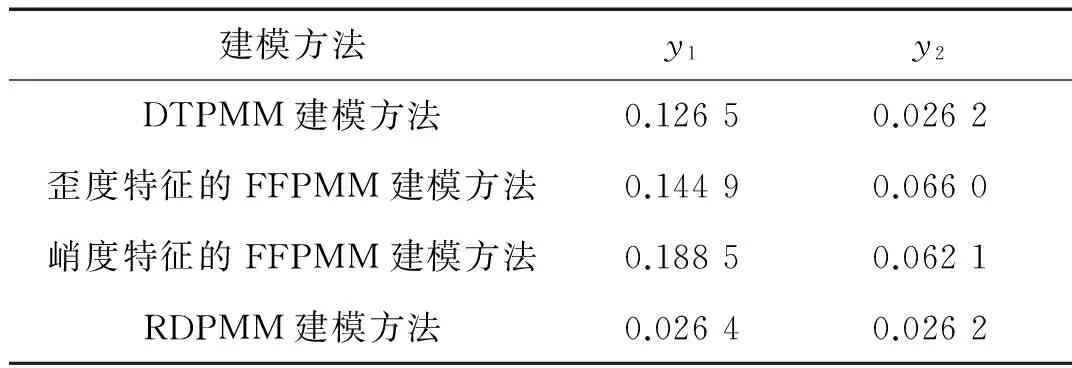
表2 正常轴承信号的四种建模方法对比结果

从表2数据可以看出， 紧致性最高的是RDPMM建模方法，其次分别是：DTPMM建模方法、歪度特征FFPMM建模方法和峭度特征FFPMM建模方法。

利用概率盒建模方法将原始振动信号的不确定性包含在概率盒中，从概率盒的图形中应该可以提取出能反映出故障特征的信息以用于模式识别。为此取概率盒图形最宽度的腰围值为特征之一，通过对实验数据的分析，发现正常状态下该值稳定在一定的范围内，故障时该值呈现出不同的波动范围。本文共从概率盒图形中提取包含式(16)和式(17)在内的6个统计特征。再以传统的无量纲特征：波形指标、脉冲指标、峰值指标、裕度指标、歪度指标和峭度指标为6个特征向量，以SVM为模式识别工具，以相同的SVM参数设置进行对比。每类轴承有120组实验数据，4类轴承，共计480组数据，其中2/3用于测试，剩余1/3用于识别，得到的正确识别率统计结果如表3所示。结果表明，本文方法的总正确识别率优于传统特征提取方法。

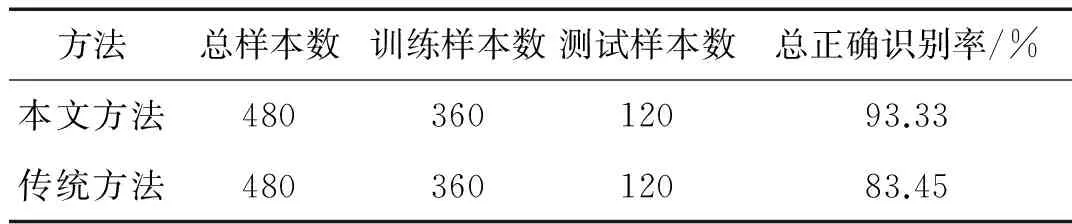
表3 本文方法与传统方法比较结果

5 结 论

(1) 提出了一种基于概率盒理论的滚动轴承故障信号的建模方法。该方法利用了概率盒在处理不确定性问题上的优势，对原始采集信号的不确定性实现了外包络，避免了特征提取带来的信息丢失现象。

(2) 针对实验数据有固定概率分布类型情况，提出的正态分布概率盒建模方法。当无固定概率分布类型时，提出故障特征概率盒建模方法作为补充方法，根据概率盒定义提出原始数据的概率盒直接建模方法，后者无需验证数据的概率分布类型，适用范围广。

(3) 以SVM为模式识别方法，对比了传统特征提取与概率盒建模方法对正确识别率的影响，结果表明，算法有效可行。

[1] 赵志宏,杨绍普,刘永强. 多小波系数特征提取方法在故障诊断中的应用[J]. 振动、测试与诊断，2015,35(2):276-280.

ZHAO Zhihong, YANG Shaopu, LIU Yongqiang．Multi-wavelet coefficient feature extraction method in fault diagnosis[J]．Journal of Vibration, Measurement & Diagnosis, 2015, 35(2):276-280.

[2] 向丹, 葛爽. 基于样本熵和流形学习的故障特征提取方法[J]. 航空动力学报，2014, 29(7):1535-1542

XIANG Dan, GE Shuang. Method of fault feature extraction based on EMD sample entropy and manifold learning [J]. Journal of Aerospace Power, 2014, 29(7): 1535-1542.

[3] 任立通，胡金海，谢寿生,等. 基于随机共振预处理的振动故障特征提取研究[J]. 振动与冲击，2014，33(2):141-146.

REN Litong, HU Jinhai, XIE Shousheng, et al. Vibration fault feature extraction based on stochastic resonance pretreatment[J]. Journal of Vibration and Shock, 2014，33(2):141-146.

[4] 唐贵基，王晓龙．基于局部均值分解和切片双谱的滚动轴承故障诊断研究[J]. 振动与冲击,2013,32(24):83-88.

TANG GuiJi, WANG Xiaolong. Fault diagnosis of roller bearings based on local mean decomposition and slice bispectrun[J]. Journal of Vibration and Shock,2013,32(24): 83-88.

[5] 隋文涛, 张丹. 平稳小波变换在轴承振动信号去噪中的应用[J]. 轴承, 2012(1):38-40

SUI Wentao, ZHANG Dan. Application of stationary wavelet transform in de-nosing of bearing vibration signal[J]. Bearing, 2012(1):38-40.

[6] KAUFMANN A, GUPTA M M. Introduction to Fuzzy Arithmetic: Theory and Applications[M]. New York : Van Nostrand Reinhold, 1985.

[7] SHAFER G. TheCombination of Evidence[J]. International Journal of Intelligent Systems, 1986(3): 155-179.

[8] HAILPERIN T. Boole’s Logic and Probability[M]. North-Holland, Amsterdam, 1986.

[9] FRANK M J, NELSEN R B,SCHWEIZER B. Best-possible bounds for the distribution of a sum-a problem of Kolmogorov[J]. Probability Theory and Related Fields,1987,74:199-211.

[10] SAVIC R. Neural generation of uncertainty reliability functions bounded by belief and plausibility frontiers[C]//European Conference on Safety and Reliability,2005,1757-1762.

[11] WALKER N. A first course in fuzzy logic[M]. Boca Raton, Florida: CRC Press, 2006.

[12] FERSON S, KREINOVICH V, GINZBURG L, et al. Constructing probability boxes and dempster-shafer structures[R].California：Sandia National Laboratories, 2003.

[13] BOUNDING B. The times to failure of 2-components systems [J]. IEEE Transaction on Reliability, 2004, 53(4):542-550.

[14] TONON F. Using random set theory to propagate epistemic uncertainty through a mechanical system [J]. Reliability Engineering and System Safety, 2004, 85:169-181.

[15] SAVIC L. Fault tree analysis in an early design stage using the Dempster-Shafer theory of evidence [J]. Risk, Reliability and Societal Safety,2007, 1(3): 99-105.

[16] OBERGUGGENBERGER M, KING J, SCHMELZER B. Imprecise probability methods for sensitivity analysis in engineering [C]//In 5th International Symposium on Imprecise Probability: Theories and Applications, Prague, Czech Republic, 2007, 6: 1130-1138.

[17] CHOJNACKI D D. Unifying practical uncertainty representations-I: Generalized p-boxes [J]. International Journal of Approximate Reasoning, 2008, 49(3): 649-663.

[18] CRESPO L G, KENNY S P, GIESY D P. Reliability analysis of polynomial systems subject to p-box uncertainties[J]. Mechanical Systems and Signal Processing, 2012, 9: 111-124.

[19] TROFFAES M C M, MIRANDA E, DESTERCKE S. On the connection between probability boxes and possibility measures Original Research Article [J]. Information Sciences, 2013, 224 (3): 88-108.

[20] BEN ABDALLAH N, MOUHOUS-VOYNEAU N, DENOEUX T. Combining statistical and expert evidence using belief functions: Application to centennial sea level estimation taking into account climate change [J]. International Journal of Approximate Reasoning, 2014, 55(1): 341-354.

Rolling bearing fault signal modeling methods based on probability box theory

DU Yi1, DING Jiaman2, LIU liqiang1

(1. City College，Kunming University of Science and Technology，Kunming 650051, China；2. College of Information Engineering and Automation，Kunming University of Science and Technology，Kunming 650500, China)

Feature extraction may lead to information loss and multi-segment-average may lead to data discarding and uncertainties in machinery fault diagnosis. In order to solve these problems, a new modeling method for mechanical fault signals based on the probability box (p-box) theory was proposed. Fault signals of rolling bearings were taken as the study object. Firstly, the original signals’ probability distribution types were analyzed. The uncertainty intervals of the probability distribution’s parameters were calculated. The p-box modeling method based on the normal distribution was proposed. Secondly, in order to overcome the identification difficulty of fault signal data’s probability distribution type, the original signals’ features were extracted. Using the ordered character of the feature signals, a p-box modeling method based on feature extraction was proposed. The similarities and differences between the skewness p-box and the kurtosis p-box were contrasted. Thirdly, based on the p-box’s definition, the original data uncertainties were projected into the p-box’s bounds a more effective p-box modeling method directly based on the original data was proposed, it did not need data’s probability distribution identification. The effectiveness and applicability of the three methods were compared using rolling bearings’ measuring data, the three methods’ validity was verified compared with the conventional feature extraction method.

rolling bearing; fault diagnosis; uncertainty; probability box theory; DS structure

国家自然科学基金(51365020;51467007)

2015-05-29 修改稿收到日期：2015-10-14

杜奕 男，博士，副教授，1977年生

丁家满 男，硕士，副教授，1974年生

TP391;TH165.3;TH133.33

A

10.13465/j.cnki.jvs.2016.19.006