随机LFM脉冲信号合成距离像方法

2016-02-08陈行勇

中国电子科学研究院学报 2016年6期

关键词：傅里叶调频多普勒

陈行勇

(91404部队，秦皇岛 066001)

基础理论

随机LFM脉冲信号合成距离像方法

陈行勇

(91404部队，秦皇岛 066001)

随机信号成像雷达结合了宽带成像和随机信号雷达技术，具有十分优良的低截获概率和抗射频干扰等特性。针对随机脉冲信号雷达合成距离像问题，给出了随机LFM脉冲信号一般模型，推导了基于随机LFM脉冲信号的合成距离像方法，分析了随机二相、脉位、脉宽、重频、调频极性等随机调制对合成距离像的影响，并从距离像移位和幅度失真等方面，分析了运动目标多普勒效应对合成距离像的影响，证明了随机LFM脉冲信号可以用于雷达合成距离像，最后对信号模型的雷达合成距离像性能、多普勒效应进行了仿真计算，验证了理论分析。

线性调频；随机信号雷达；高分辨距离像；多普勒效应；傅里叶变换

0 引言

随机信号雷达使用微波随机信号或低频随机信号，与使用确定信号雷达相比，在目标发现能力、测量参数的精确度、鉴别力、抗干扰能力及电磁兼容能力等方面具有优越性[1]。自20世纪60年代以来，国内外研究者就一直在研究随机信号雷达理论及其实现[2]。2007年，Axelsson提出一种新的随机频率步进雷达体制[3]，该体制兼具步进频率雷达和噪声雷达的特点，可以降低系统瞬时带宽和数据采样率，且易于实现。在Axelsson研究基础上，文献[4]分析了随机频率步进信号的模糊函数统计特性、抗干扰性和Range-Doppler SAR成像方法。文献[5]基于步进频率和随机噪声技术设计了一种新的超宽带雷达信号。文献[6]使用伯努利映射(Bernoulli Mapping)决定发射信号频率序列，提出了一种基于混沌的随机频率步进雷达信号。以上研究表明，利用匹配滤波技术，随机频率步进信号可用于雷达成像，同时又有常规频率步进信号所不具有的抗干扰性能。

线性调频脉冲压缩雷达信号具有良好的作用距离、距离分辨力和抗干扰能力，通过其频谱分析方法合成距离像是雷达目标识别的重要手段[7, 8]，因而在现代雷达中广泛使用。本文给出了随机LFM脉冲信号一般模型，推导了基于随机LFM脉冲信号合成高分辨距离像的方法，分析了多普勒效应导致的距离像移位和幅度失真，分析了随机二相、脉位、脉宽、重频、调频极性等随机调制对随机LFM脉冲信号合成距离像的影响，最后进行了仿真计算。

1 随机LFM脉冲信号一般模型

线性调频信号具有系统易于实现，功耗低，复杂度低等特点，并且是一种大时宽带宽信号，可利用目标回波中的频率对应目标的径向距离变化，从而通过频谱分析的办法来得到目标沿径向分布的一维距离像[9]，被广泛应用在雷达和通信系统中。

基于以上分析，本文提出的随机LFM脉冲信号一般模型如图1所示。信号的基本形式为线性调频脉冲信号，脉冲相位、调频极性、脉宽和重频都为随机值。

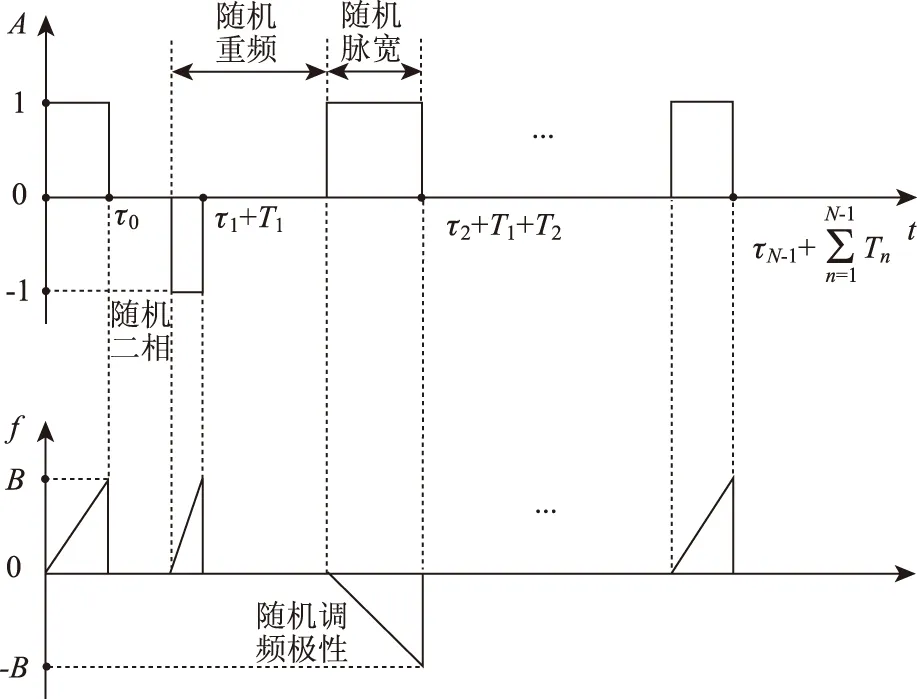
图1 随机LFM脉冲信号一般模型

如图1所示，设N为脉冲个数，i=0,1,…N-1，i+1为脉冲序号。以第一个脉冲起始时刻为0时刻，rect(t)为矩形函数，则t时刻随机LFM脉冲信号一般模型的第i+1个脉冲发射信号表达式为

(2)

其中A为脉冲幅度，f0为发射载频的基频分量，当i=0,1,…N-1时，τi>0为第i+1个脉冲随机宽度，Ti为第i+1个脉冲随机重复周期，且对于i1≠i2，τi1和τi2以及Ti1和Ti2相互独立，常量B为单个脉冲信号带宽，ki=B/τi为第i+1个chirp信号的随机调频斜率，bi∈{1,-1}和di∈{1,-1}为二元随机序列。当di=1时，线性调频信号采用上调频，则调频率为正；当di=-1时，线性调频信号采用下调频，则调频率为负。

2 随机LFM脉冲信号合成距离像方法

2.1 合成距离像方法

根据散射点模型理论，设目标散射点为理想的几何点，可以近似等效为N个等间隔Δr的散射中心构成的一离散线性系统的冲激响应，记为h(n)(n=0,1,2,…，N-1)，合成距离像的原理就是由回波信号恢复h(n)。

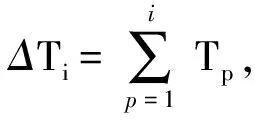
(2)

其中c为光速，设第1个散射中心点处有一理想参考点，第i+1个脉冲照射该理想参考点的归一化回波信号为

(3)

将每个脉冲的目标回波信号与以上对应脉冲的参考信号混频输出得归一化中频信号[9, 10]

(4)

设m=0,1,…,N-1,将上式幅度因子归一化，并在一个脉冲扫频周期内的ΔTi+mτi/N时刻采样，得采样序列

H[i,m]=sRI(i,ΔTi+mτi/N)=

(5)

由于扫频时间较短，假设目标各散射中心径向速度相同，即vn=v，则上式变为

(6)

φ(i,m)=φ0+φ1·m+φ2·m2

(7)

2ndikivΔrΔTi+2dikiR0vΔTi)

(8)

(9)

(10)

一般情况下，v≪c，(6)式中的1+2v/c≈1。根据奈奎斯特采样定理，若选择调频率和脉冲宽度，使得目标距离像恰好不出现混叠[9, 10]，则Δr=c/(2B)=c/(2kiτi)，代入(6)式可得

(11)

若目标各散射中心无径向运动，则v=0，上式变为

(12)

由此可得

H[i,m]=

(3)

(14)

上两式中，DFT[·]和IDFT[·]分别为对m或n的离散傅里叶变换和逆离散傅里叶变换。由(14)式可知，目标距离像可由单个脉冲回波中频信号采样的逆离散傅里叶变换或傅里叶变换取模获得。

若Q为大于等于1的整数，在一个脉冲扫频周期内的ΔTi+mτi/QN时刻采样得采样序列，由(6)式可得

(15)

h′(n)为h(n)从N到QN-1补零构成的延长序列。由上式可知，依据每个脉冲di取值的不同，计算离散傅里叶变换或逆离散傅里叶变换，可得距离像尾端补零序列。

2.2 随机调制影响分析

假设目标各散射中心无径向运动，下面分析信号的随机调制对合成距离像的影响。

2.2.1 随机二相

由式(14)可知，对采样信号计算DFT或IDFT后取模，可消除随机二相对高分辨距离像的影响。

2.2.2 随机脉宽

由于对回波信号每个脉冲采样点数相同，脉宽宽度就决定了采样率，因此要求随机脉冲宽度不能太小，否则数字信号处理硬件不能满足要求。根据(4)式，对第i+1个脉冲采样率为N/τi，假设要求最大采样率不能大于fs，则最小脉冲宽度τmin应满足N/τmin≤fs，即τmin≥N/fs。

2.2.3 随机重频

由式(9)可知，随机重频1/Ti通过(c+2vi)ΔTi项影响一次相位项因子。对于高速运动目标，在一个脉冲周期串内，若脉冲重复周期较大(随机重频较小)，则通过多个脉冲积累，将造成合成距离像移位，定量分析见3.3多普勒效应分析。

2.2.4 随机线性调频极性

由式(14)可知，随机线性调频极性决定对信号采样所进行的是傅里叶变换还是逆傅里叶变换，对合成距离像无影响。

2.3 多普勒效应分析

2.3.1 常数项

常数项φ0不包含离散傅里叶变换频域因子m，相当于对h(n)的相位加权，对h(n)的位置和幅度无影响，对采样点列求DFT或IDFT后取模可消除常数项对一维距离像影响。

2.3.2 一次相位因子

一次相位因子φ1的作用相当于频域移位采样，使回波脉冲采样求DFT或IDFT后得到的h(n)循环移位L单元，对一维距离像形状无影响。由式(9)可知，除目标速度和距离外，多普勒效应引起的距离像移位主要受随机调频极性、随机脉宽和随机重频的影响。距离像移位点数L由下式计算

L=⎣N·(φ1-⎣φ1」)」

(16)

其中，⎣·」表示向下取整运算，上式也即走动的距离单元数的计算公式。

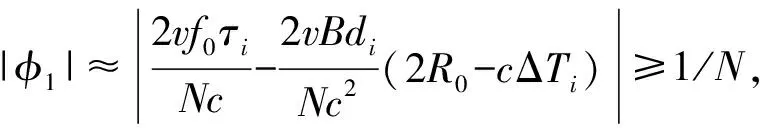
(17)

2.3.3 二次相位因子

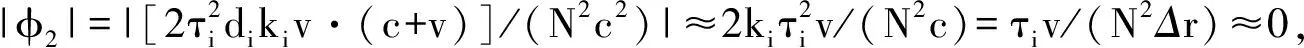
v≤vb=N2πΔr/[2τi(N-1)2]

(18)

由此可知，脉冲宽度随机变化的范围不能太大，否则当目标运动时的多普勒效应可能产生较大的二次相位偏移，从而使距离像失真。

3 仿真计算

设bi∈{1,-1}和di∈{1,-1}为二元随机序列，τa=1 μs，Ta=10 μs，τi=(1+αδi)·τa，Ti=(1+βμi)·Ta，其中i为脉冲序号，δi和μi为[0,1]上的均匀分布，α∈[0,1],β∈[0,1]。取α=0.2，β=0.3。设随机LFM脉冲信号参数为：N=128，发射频率f0=10 GHz，chirp子脉冲带宽B=kiτi=500 MHz，共享信号一个脉冲串共发射128个脉冲。由以上参数可得距离分辨率为Δr=c/(2B)=0.3 m。以待成像目标与雷达最近端的分辨单元为坐标原点，设目标有5个强散射点，且5个强散射点距离原点距离分别为13Δr、32Δr、55Δr、64Δr和97Δr，其归一化散射强度之比为1∶8∶3∶6∶4，第一个分辨单元距离雷达的径向距离为20 km。

设d1=1，τ1=1 μs,ΔT1=10 μs，由(17)式和(18)式计算得va=20900 m/s，vb=478450 m/s。不考虑噪声影响和采样的幅度损失，以下分析信杂比和目标运动速度对合成距离像的影响。

3.1 合成距离像仿真

假设目标静止，雷达接收信号的信杂比为SCR，对一个脉冲串内的第一个脉冲回波信号进行处理，获取的目标距离像，图2给出了v=0时不同信杂比下合成距离像。

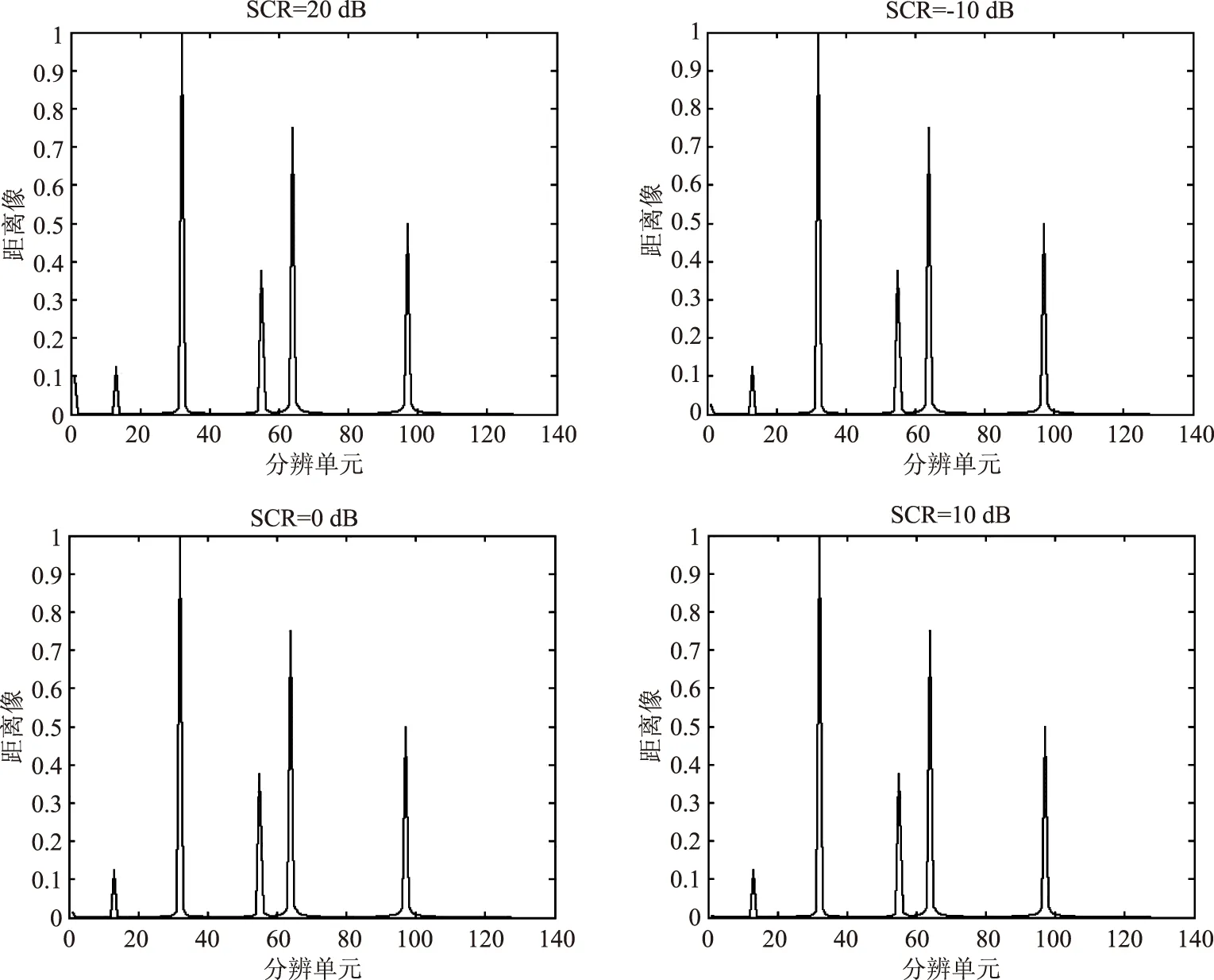
图2 不同信杂比条件下随机LFM脉冲信号合成距离像

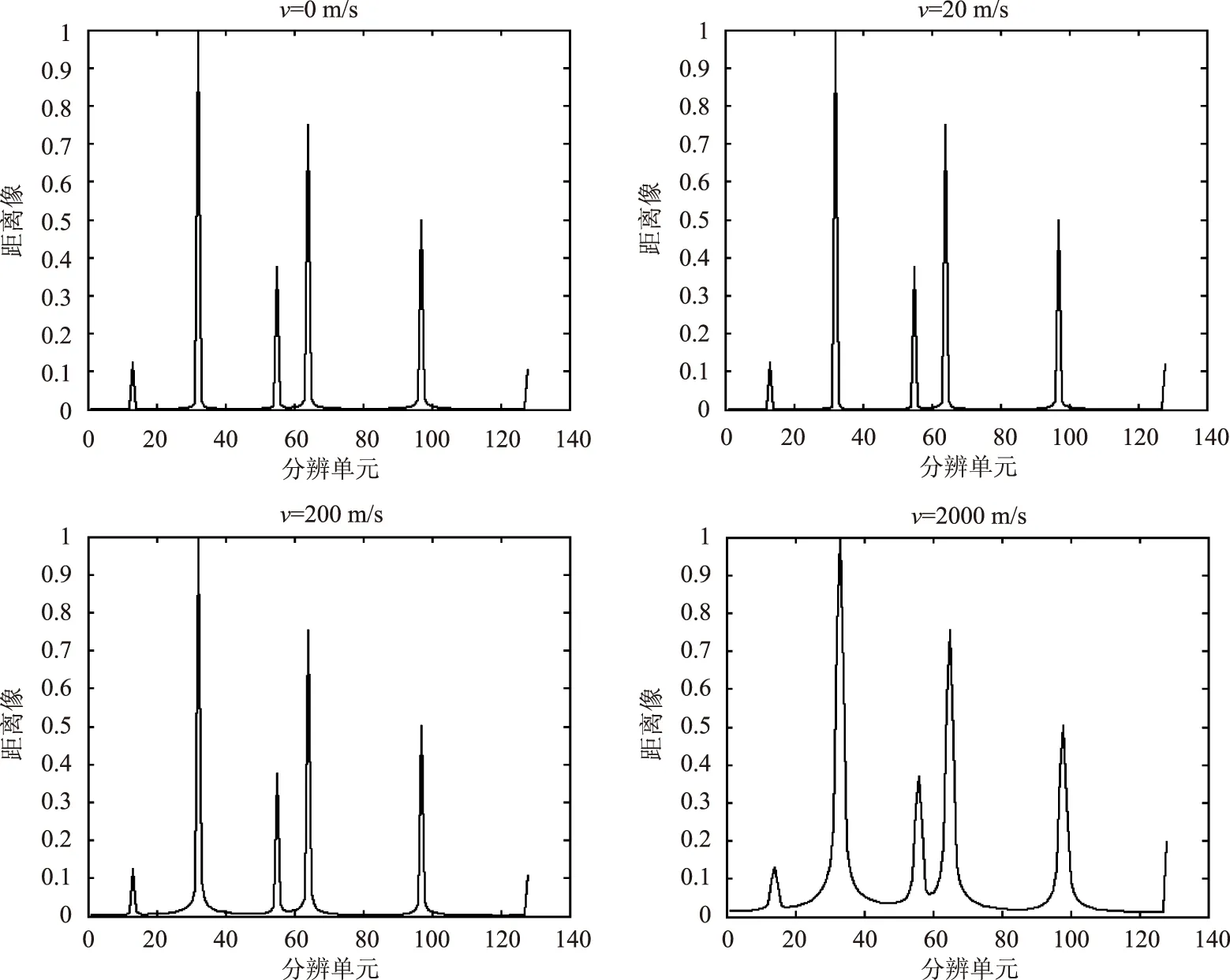
图3 不同目标径向速度条件下随机LFM脉冲信号合成距离像

由图2可知，随机二项、随机脉宽、随机重频和随机线性调频极性对静止目标距离像基本没有影响，与确定的线性调频信号获取距离像结果一致。如图所示，在SCR=-20 dB时，合成距离像会在目标起始点h(0)处产生“假像”，但对其他强散射点影响较小。经分析，这是由于matlab仿真软件产生的高斯白噪声杂波非理想的全频谱模型，其杂波能量主要集中在零频和低频附近，导致在h(0)处产生“假像”，实际工程不会出现此问题。

3.2 多普勒效应仿真

若目标运动，对一个脉冲串内所有脉冲获取的目标距离像取平均得最终一维距离像，分析多普勒效应对随机LFM脉冲信号合成距离像的影响。图3给出了SCR=20 dB时不同目标速度下合成距离像。

由图3可知，对一般的运动目标，其速度一般远小于va和vb，对距离像移位和幅度几乎无影响，只有当目标速度增大至2000 m/s时，目标距离像才会产生较小畸变，但5个强散射点依然可以明显分辨。

4 结语

随机脉冲信号除了可用于雷达探测与目标识别外，也用于雷达与干扰一体化共用信号设计，因而，随机信号波形设计是综合射频系统的关键技术之一。本文主要研究了随机LFM脉冲信号的一般模型，证明了该信号可以用于获取目标的高分辨距离像。理论上雷达成像和雷达干扰对信号的规则性和随机性的要求存在冲突，对信号的随机性应综合考虑，使得雷达成像和雷达干扰性能达到平衡或有所侧重。

[1] 刘国岁, 顾红, 苏卫民. 随机信号雷达[M]. 北京: 国防工业出版社, 2005.

[2] Liu G S, Gu H, Su W M. Development of random signal radar[J]. IEEE Transactions on Aerospace and Electronic Systems. 1999, 35(3):770-777.

[3] Axelsson Sune R J. Analysis of Random Step Frequency Radar and Comparison With Experiments[J]. IEEE Transactions on GeoScience and Remote Sensing. 2007, 45(4):890- 904.

[4] 彭岁阳, 张军, 沈振康. 随机频率步进雷达成像分析[J]. 国防科技大学学报. 2011, 33(1):59-64.

[5] Gu X, Zhang Y H, Zhang X K. Stepped Frequency Random Noise UWB Radar Signal[C]. The 3rd International Asia-Pacific Conference on Synthetic Aperture Radar. Seoul: IEEE, 2011. 1-4.

[6] Zhang Y, Hu W, Wang L, et.al. A Novel Random Stepped Frequency Radar Using Chaos[C]. 2014 IEEE Radar Conference. Cincinnati: IEEE, 2014,662-665.

[7] 陈行勇. 微动目标雷达特征提取技术研究[D]. 长沙: 国防科学技术大学博士学位论文,2006.

[8] 郭尊华, 李达, 张伯彦. 雷达高距离分辨率一维像目标识别[J]. 系统工程与电子技术. 2013, 35(1):53-60.

[9] 黄德双. 高分辨雷达智能信号处理技术[M]. 北京: 机械工业出版社, 2001.

[10]许小剑, 黄培康. 雷达系统及其信息处理[M]. 北京: 电子工业出版社, 2010.

关于《中国电子科学研究院学报》启用在线采编系统的通知

尊敬的作者：

您好,为了更好地服务于广大作者、审稿专家和读者,方便查询论文信息、投稿、询稿及审稿,提高杂志工作效率,《中国电子科学研究院学报》编辑部引进了期刊在线采编系统,目前已经正式开通，请您登陆如下网址，并注册进行投稿。在线采编系统启用后，我们将不再接收电子邮件投稿，造成不便，敬请谅解。

《中国电子科学研究院学报》在线采编系统网址：http://kjpl.cbpt.cnki.net。

在使用中如果有任何问题，请您及时与编辑部联系，联系电话：010-68893411

邮箱：dkyxuebao@vip.126.com

《中国电子科学研究院学报》编辑部

2016年4月20日

A Method of Synthesizing Range Profile with a Random LFM Pulse Signal

CHEN Hang-yong

(PLA Unite 91404, Qing huangdao, Hebei, 066001, China)

Radom signal imaging radar combines the technologies of wide-band imaging and random signal radar, which brought about such superiorities as very good low probability of interception and radio-frequency anti-interfere. As for the problem of synthesizing range profile with random pulse signal radar, a general model of random LFM pulse sharing signal is built. Then, a method of synthesizing range profile is derived with random LFM pulse signal, and the effect on synthesizing range profile is analyzed which caused by random modulations, including random binary phase, random pulse position, random pulse width and random pulse repetition frequency and random polarity linear frequency modulations. Doppler Effect on synthesizing range profile of moving target is analyzed, including range profile shift and amplitude distortion. Some simulations on radar imaging performance and Doppler Effect are provided for verified the theoretic analysis.

Linear Frequency Modulation；random signal radar；high resolution range profile；Doppler effect；Fourier Transform

10.3969/j.issn.1673-5692.2016.06.014

2016-06-01

2016-09-06

：A

1673-5692(2016)06-636-06