基于动态子结构法的复合材料加筋板的振动特性

钱若力，王瑞鹏，李顶河

（中国民航大学航空工程学院，天津 300300）

基于动态子结构法的复合材料加筋板的振动特性

钱若力，王瑞鹏，李顶河

（中国民航大学航空工程学院，天津 300300）

采用动态子结构法中的固定模态综合法研究复合材料加筋板的振动特性。首先，基于逐层/实体元方法建立板和加强筋两个子结构的控制方程。然后，在固定界面下建立子结构的模态空间并将其控制方程转换成模态空间下的控制方程。最后，根据板和加强筋相互连接区域的内力平衡和位移协调条件，建立固定界面模态下的总体控制方程。通过数值算例将本文方法与MSC软件分析结果进行对比，从而论证该方法的正确性。此外，还对复合材料加筋板进行自由振动分析，研究结果对于分析加筋板结构具有一定的指导意义。

动态子结构法；固定界面模态综合法；加筋板；自由振动；复合材料

在工程应用领域，有限元法在结构性能分析方面具有很强的通用性，但对于比较复杂且细致的大型结构，在进行有限元划分时，需对结构进行较为稠密的网格离散，此时对结构进行分析所需计算量大，尤其是求解频率和振型的特征值问题，因此有必要引入动态子结构法（DSM，dynamic substructure method），以降低结构分析时所需庞大的计算量。该方法是对大型复杂结构系统进行动力分析的有效方法，且已成为一种常规方法[1-2]。

动态子结构法具有大幅降低计算成本的优势，因此在航空运载器、核反应装置、地面建筑以及复杂机械设备等设计和分析方面得到广泛应用[3]。按照子结构低阶模态参数的不同，动态子结构法可分为自由界面、固定界面和混合界面等3类模态综合法。固定界面模态综合法在用子结构中低阶模态信息表示高阶模态信息时，不存在因刚体模态所导致的奇异刚度阵求逆问题，计算过程简单，应用较广泛[4]。Hurty[5]首先提出模态坐标和模态综合的概念，然后基于动力学原理建立固定界面模态综合法。Craig等[6]进一步改进，提出常用的固定界面模态综合法，即Craig-Bampton固定界面模态综合法。宋景涛[7-8]研究了舵机基座系统的子结构建模方法，运用ANSYS提供的固定界面模态综合法对舵机基座系统建模，并求出结构的固定频率，并且和有限元方法分析结果相比较，研究结果表明：固定界面模态综合法与常规有限元法分析出来的结果非常吻合，同时还提高前后处理的效率。王菲[9]采用约束模态综合法分析土-高层框架结构，并与有限元软件的仿真结果对比，发现两者得到的前8阶频率值非常接近，约束模态综合法可达到有限元软件的求解精度，表明该方法适用于土-高层框架结构的模态分析。王燕华[10]采用动态子结构法分析异形桥梁的自由振动特性，并将界面位移综合法、模态综合法与ANSYS有限元仿真结果分别进行对比，结果表明：界面位移综合法分析自由振动特性时，随着模态阶数递增，其分析与仿真结果的偏离越大。对于模态综合法，固定界面模态综合法的求解精度非常好，低阶模态频率值及振型几乎接近真实值，随着模态阶数的递增，误差增大，但可通过增加选取的主模态阶数来控制高阶误差。自由界面模态综合法的求解精度同样非常好，但在分析过程中需对各个子结构作特殊处理，且其坐标变换过程比较复杂。因此采用固定界面模态综合法不仅可保证求解精度，而且操作过程相对简单，是比较适合的方法。

加筋板结构在航空航天、海洋船舶、土木工程等领域应用广泛，其振动特性对结构有至关重要的影响，如设计人员需要在船舶设计阶段对船体振动响应作出准确预报，同时满足频率储备要求，以达到实际应用要求[11-12]。但实际应用中的加筋板结构多为大型结构，考虑到固有模态综合法适用于大型复杂结构分析，能够保证计算精度、操作简单，故选择该方法对加筋板结构进行振动特性分析。在分析结构之前，将结构按照一定的原则分成若干个子结构，接着分析这些子结构的动力特性，保留其低阶主要的模态信息，然后根据子结构相互连接区域的协调关系，组装成总体控制方程，从而可分析整个结构的振动特性。

1 固定界面模态综合法

在固定界面模态综合法中，首先将整体结构分为若干个子结构。对于加筋板结构，将其划分为板和加强筋两个子结构，如图1所示。

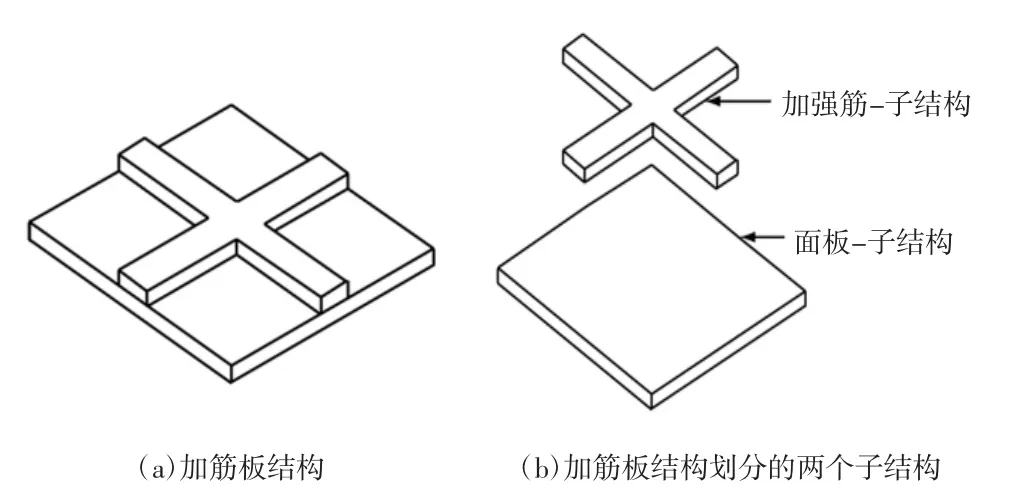
图1 加筋板结构及其划分的子结构Fig.1 Stiffened plate structure and its substructure

加筋板结构采用逐层/实体元[13]建模分析。分析过程中，板采用逐层法建立其控制方程，加强筋采用三维实体有限元法建立其控制方程，分别对两个子结构分析如下：

首先，分析加强筋结构。基于三维实体有限元法，利用六面体实体单元离散加强筋结构，建立运动方程

其中：Ms、Ks和Fs分别为加强筋的质量矩阵、刚度矩阵和载荷向量；和Us分别为节点的加速度矩阵和位移矩阵。将加强筋所有节点位移的位移自由度分成两类：板和加强筋接触部位的节点划分为外部自由度；非接触部位的节点称之为内部自由度。依据这样的划分，加强筋的控制方程可重新整理为

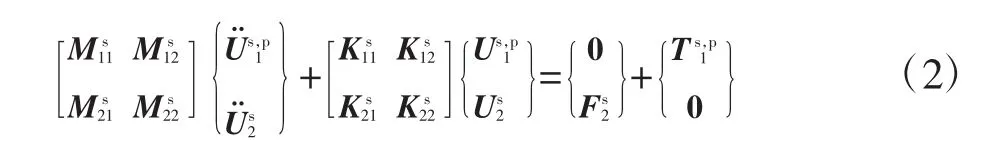
其中：上标s、p分别代表加强筋和板，下标1和2分别代表外部自由度和内部自由度；分别代表加强筋的外部加速度向量和内部加速度向量和分别代表加强筋的外部位移向量和内部位移向量和分别是加强筋的外载荷向量和板与加强筋相互作用力向量。令接触界面固定，即由式（2）可得固定界面子结构的自由振动方程为

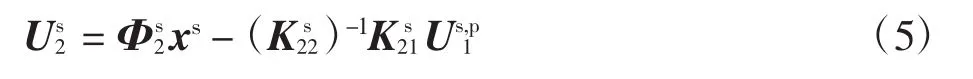
式（5）可扩展为

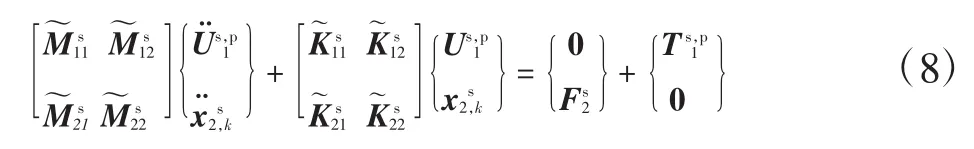
式（8）为固定界面模态下的结构自由振动方程，具体形式如下：

质量矩阵的表达式为

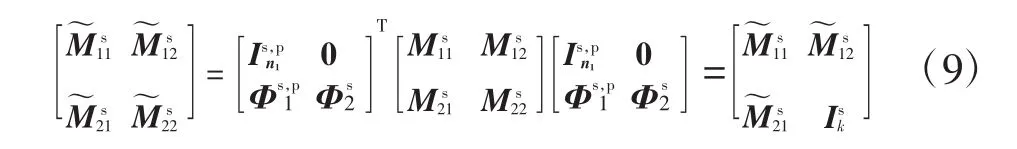
刚度矩阵的表达式为

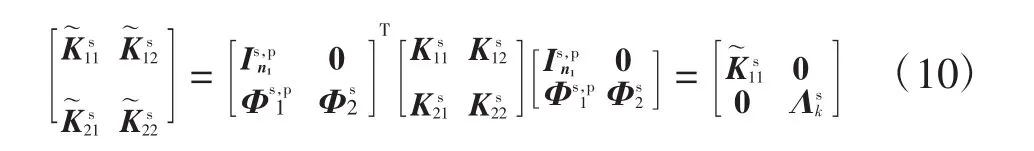
在此基础上，将式（9）、式（10）代入式（8）中，得到模态坐标空间下加强筋的自由振动方程为

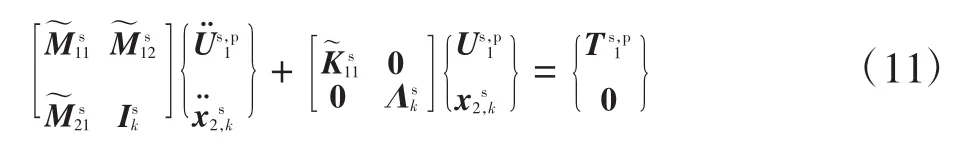
然后，采用逐层法分析板结构，建立运动方程。逐层法是先假设位移模式，厚度方向上的位移插值点位于层合板壳的表面和层间界面上，用拉格朗日插值函数将假设位移模式离散为平面位移和厚度方向位移

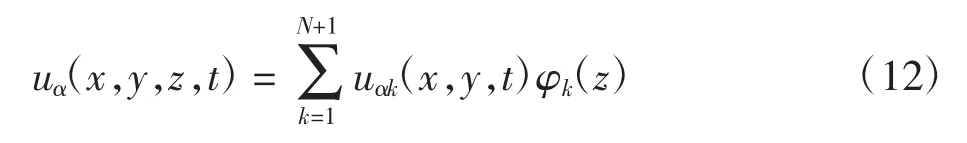
其中：α表示x、y和z方向上的位移分量；φk为厚度方向上的一维拉格朗日插值函数；N为数学层数量；uαk为位移函数在厚度方向上的节点值；k为厚度方向上插值点的编号。根据Hamilton原理得到板逐层理论的运动方程，接着采用形函数再次对平面位移进行数值离散，板逐层理论的运动方程进一步分析，最终得到板的逐层理论运动方程的有限元列式，即板逐层理论的控制方程，其形式为

其中：Mp、Kp和Fp分别是板的质量矩阵、刚度矩阵和载荷向量为结点的加速度矩阵和位移矩阵。

在得到板的控制方程后，对其控制方程进行重新整理，将板所有节点位移的自由度分成两类：板和加强筋接触部位的节点划分为外部自由度；非接触部位的节点划分为内部自由度。依据这样的划分，重新整理板的控制方程。进一步将控制方程转换为固定界面模态下的控制方程，该过程与加强筋的类似。从而得到板的固定界面模态下的自由振动方程为

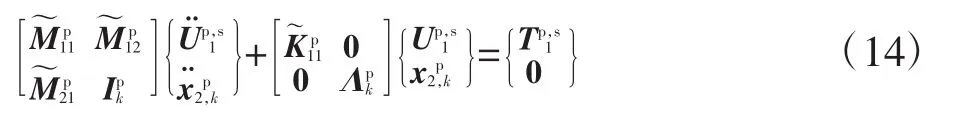
最后，将加强筋和板在固定界面模态下的控制方程拼装在一起。根据所得到的加强筋和板的控制方程以及接触部位的位移连续条件及内力平衡条件，即将式（11）第一行和式（14）第一行相加，得

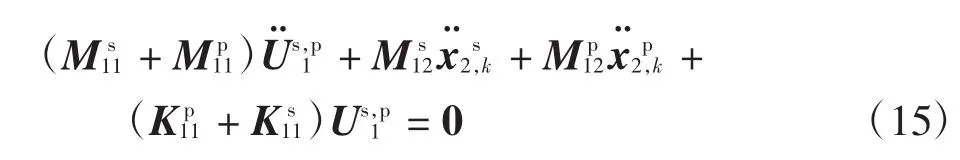
将式（11）第二行、式（14）第二行和式（15）联立，得到整体结构系统的自由运动方程为

其中，整体结构的结点位移为

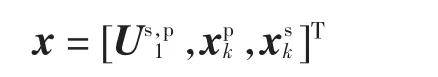
质量矩阵为

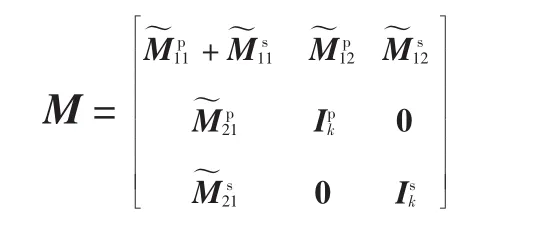
刚度矩阵为

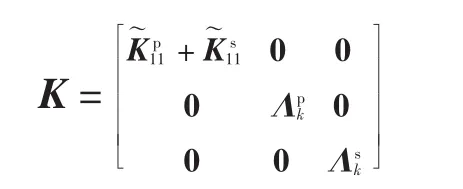
根据式（16）可对加筋板结构进行自由振动分析，得到结构的固有频率和振型，其中振型为固定界面模态下的振型，需要经过如下转换

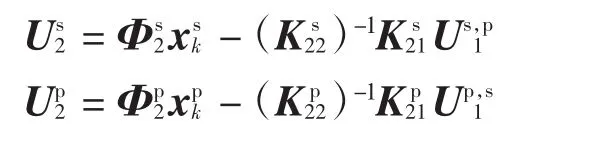
2 数值算例

2.1 各向同性板的加筋板结构

本文利用固定界面模态综合法对加筋板结构进行自由振动特性分析。将该方法写成Matlab程序，并得出结构的固有频率。

加筋板结构采用逐层/实体元建模分析：加强筋采用三维有限元法建模，板采用逐层法建模，建立各自的控制方程。界面固定情况下分别取板和加强筋的前10、20和30阶模态组成模态集，将板和加强筋的控制方程转换为各自模态集下的控制方程，在基于板和加强筋连接处的内力平衡和位移协调，进一步拼装成结构在模态集下的总体控制方程。

本算例中，加筋板结构对边固支，结构的几何尺寸和有限元网格划分如图2所示。板和加强筋的材料参数相同：E=6.8×104Pa，μ=0.3，ρ=2.7×103kg/m3。为验证模态综合法的结果，基于有限元分析软件MSC. Patran建立加筋板结构的有限元模型，并利用Nastran软件求解，板采用四结点Quad4单元离散，加强筋采用八结点六面体单元离散。将固定界面模态综合法和有限元软件分析结果对比，其结果如表1和图3所示。

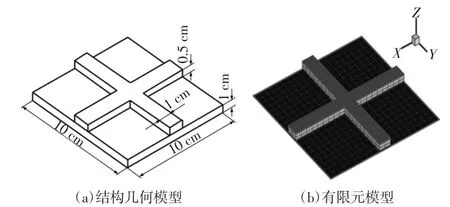
图2 结构几何模型和有限元模型Fig.2 Structural geometry and finite element model

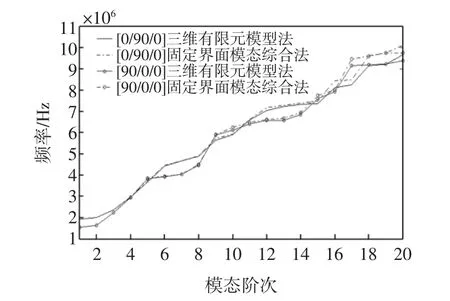
图3 k=10时固定界面模态综合法与三维有限元模型的前20阶固有频率Fig.3 First twenty natural frequencies obtained by DSM and MSC at k=10

从表1可看出，k=10时在前8阶频率中，固定界面模态综合法与三维有限元模型分析结果接近，其相对误差不超过1%，当k=20和k=30时，本文方法的分析结果精度更高，说明当所取模态个数增加时，分析结果会更加准确。同时，随着频率阶次增加，分析结果精度降低，尤其从第9阶频率开始，固定界面模态综合法分析结果的相对误差有变大的趋势。

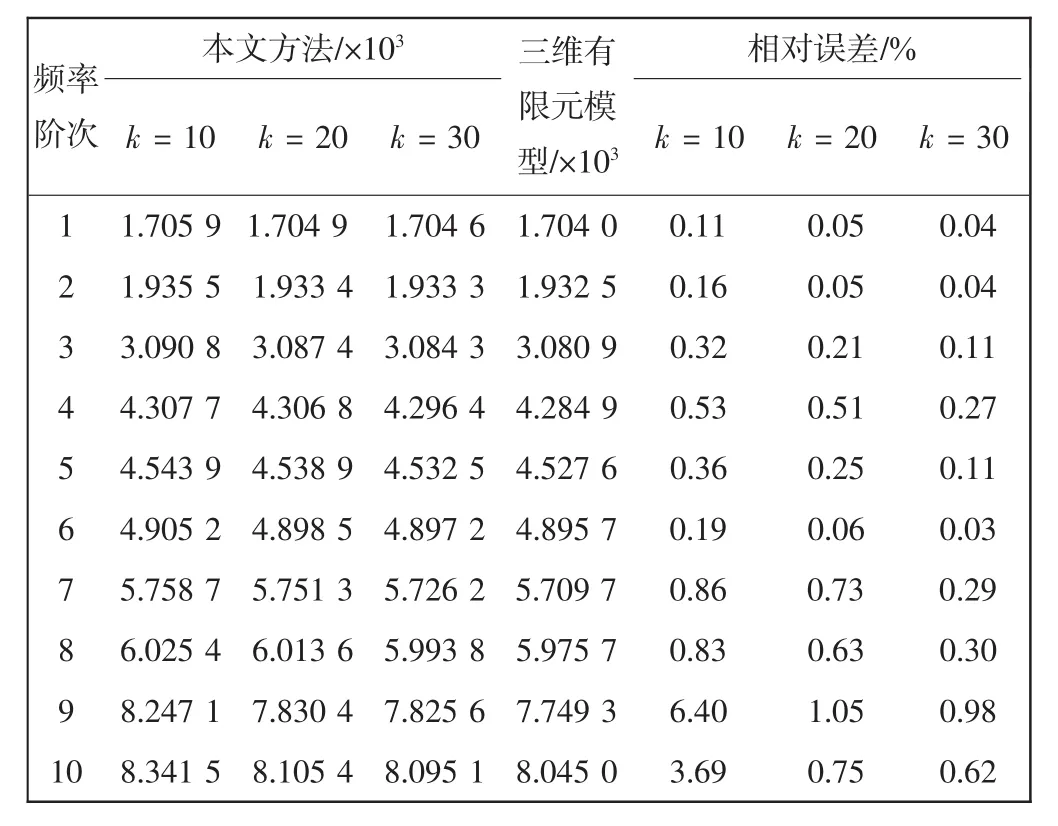
表1 固定界面模态综合法与三维有限元模型的前10阶固有频率Tab.1 First ten natural frequencies obtained by DSM and MSC

2.2 各向异性板的加筋板结构

本算例中，板为层合板结构，加筋板结构的边界条件、几何尺寸和有限元网格与上例相同。板采用各向异性材料，其材料参数如表2所示。板采用[0/90/0]和[90/0/0]铺设方式的复合材料，用固定界面模态综合法分析加筋板结构的自由振动特性。在界面固定情况下分别取板和加强筋的前k=10、k=20和k=30阶模态组成模态集，其分析结果如表3所示。

表2 板和加强筋材料参数Tab.2 Material parameters of plate and stiffener

从表3和图3可以看出，加筋板结构在对边固支情况下，对于[0/90/0]和[90/0/0]铺设方式，固定界面模态综合法与三维有限元模型法的前10阶固有频率都比较吻合；k=20和k=30，即选取的模态个数增加时，本文方法结果的精度进一步提高；随着频率阶次增加，本文方法分析结果与三维有限元模型法的结果差异有变大的趋势。此外，不同的铺设方式对结构的频率有较小影响，使频率在一定范围内波动，但变化趋势一致。总体上，固定界面模态综合法在分析复合材料结构的低阶频率时同样具有较高的精度。

然后对比本文方法与三维有限元模型法所得总体控制方程的自由度，如表4所示。在表4中，板的节点数为441个，加强筋的节点数为351个，板与加强筋相互连接区域的节点是117个，选取前10阶模态组成模态集，即k=10。

从表4可以发现，固定界面模态综合法在分析结构的自由振动特性时，相比于三维有限元模型法确实能够减少总体控制方程的自由度，降低算法对内存需求。在划分子结构时，应注意子结构间的节点尽可能少，这样有益于降低总体控制方程的自由度。需明确的是，本文方法虽然降低了总体控制方程的阶数，但是计算量并没有显著减少，主要原因是增加子结构动力特性分析及原物理坐标下与固定界面模态空间下控制方程的转换过程。当分析比较复杂的结构时，本文方法得到的总体控制方程阶数相对于三维有限元模型法来说会明显降低，这会大大减少自由振动特性分析时计算机使用内存，同时也说明动态子结构法在分析大型复杂结构方面具有独特优势。

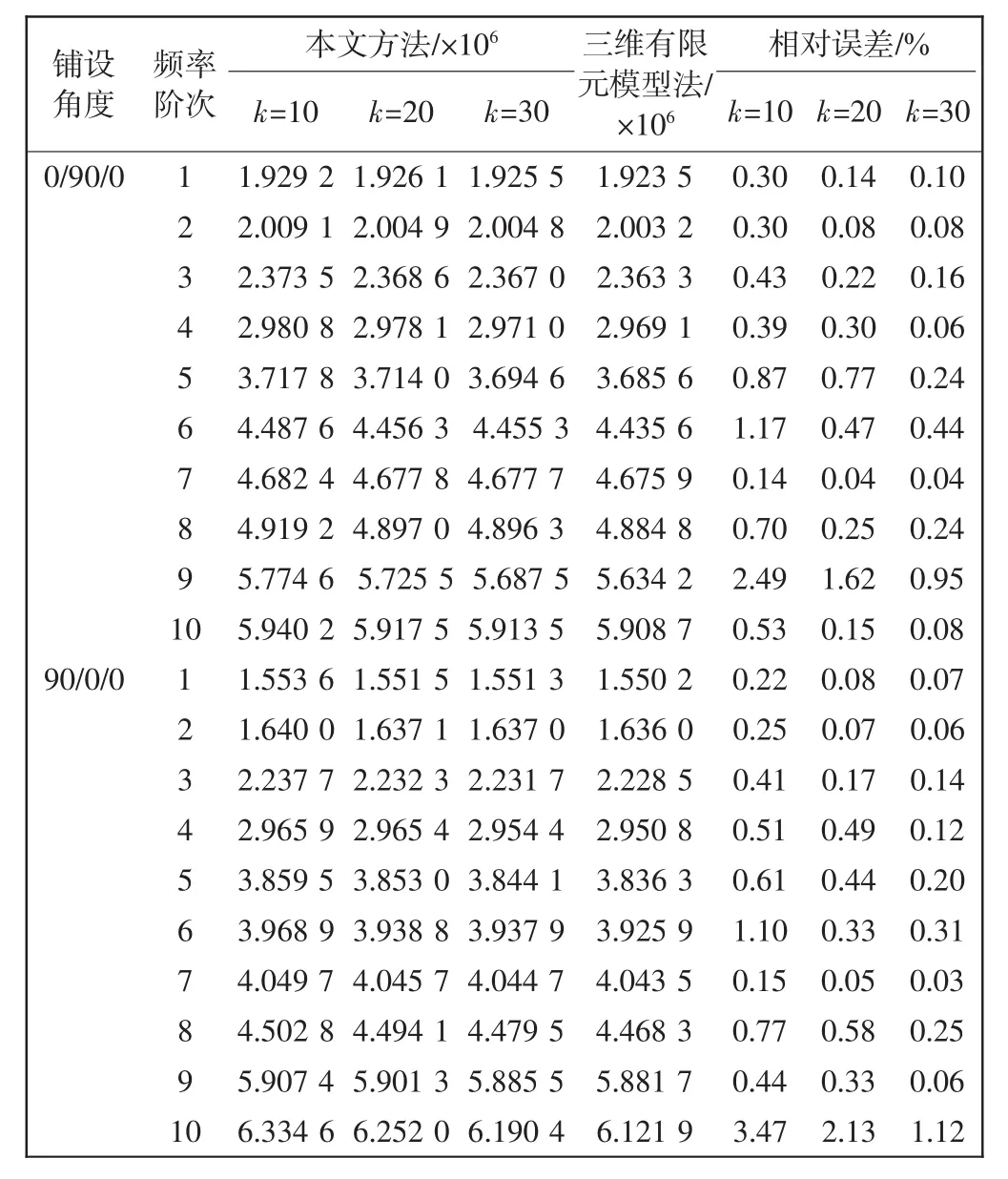
表3 固定界面模态综合法与三维有限元模型前10阶固有频率Tab.3 First ten natural frequencies obtained by DSM and MSC

表4 固定界面模态法与三维有限元总控制方程自由度Fig.4 Freedoms degrees of governing equations obtained by DSM and MSC

3 结语

本文分析加筋板结构在对边固支条件下的振动特性，采用固定界面模态综合法，将整个结构划分为两个子结构，将其控制方程转换为各自模态集下的控制方程，结合连接界面的内力平衡和位移协调，组成加筋板结构的总体控制方程，进而分析结构的固有频率，并与三维有限元法结果相比，证明固定界面模态综合法在分析低阶频率时确实有较高精度。在此基础上，分析采用复合材料板加筋板结构的振动特性，得出以下结论：

1）固定界面模态综合法与有限元法的前10阶固有频率都比较吻合，精度比较高；选取的模态个数增加时，本文方法分析结果的精度进一步提高；随着阶次增加，其分析结果与三维有限元法的分析结果相差越来越大；

2）不同的铺设方式对结构的频率有较小影响，使得频率在一定范围内波动，但变化趋势一致；

3）固定界面模态综合法能够降低计算量。在子结构划分过程中，应尽量选择较少联系界面，这样可降低总体控制方程的阶数。

[1]张 雄,刘 岩.计算动力学[M].北京:清华大学出版社,2007.

[2]王永岩.动态子结构方法理论及应用[M].北京:科学出版社,1999.

[3]郑刚铁,刘明辉.子结构模态综合的研究进展与应用[C]//第十届全国振动理论及应用学术会议论文集(2011)下册.南京:南京航空航天大学,2011.

[4]王 缅,郑钢铁.一种改进的固定界面模态综合法[J].宇航学报,2012, 33(3):291-297.

[5]HURLY W C.Dynamic analysis of structural systems using component modes[J].AIAA Journal,1965,3(4):678-685.

[6]CRAIG R R,BAMPTON M C C.Coupling of substructures for dynamic analysis[J].AIAA Journal,1968,6(7):1313-1319.

[7]宋景涛.舵机-基座动力模型建立及动态子结构分析[D].上海:同济大学,2008.

[8]宋景涛,方明霞.模态综合法在ANSYS中的应用[J].计算机辅助工程,2007,16(3):145-148.

[9]王 菲.地基土-高层建筑相互作用的动态子结构法[D].天津:天津大学,2010.

[10]王燕华.基于动态子结构法的异形桥梁动力特性研究[D].长春:吉林大学,2014.

[11]黄海燕,王德禹.加筋板结构的自由振动分析[J].船舶工程,2008, 30(6):1-3,18.

[12]石 鹏.曲型加筋板、壳结构的建模方法与分析研究[D].北京:北京理工大学,2015.

[13]LI DINGHE,QING GUANGHUI,LIU YAN.A layerwise/solid-element method for the composite stiffened laminated cylindrical shell structures [J].Composite Structures,2013,98:215-227.

（责任编辑：党亚茹）

Free vibration analysis of stiffened composite plate structure based on dynamic substructure method

QIAN Ruoli,WANG Ruipeng,LI Dinghe
（College of Aeronautical Engineering,CAUC,Tianjin 300300,China）

Fixed-interface modal synthesis technique based on dynamic substructure method is used to analyze free vibration performance of stiffened plate structure.First of all,governing equations of plate and stiffeners are established based on layerwise/solid element.And then,substructures’modal space is established and governing equations are converted into equations under modal space.Finally,basing on governing equations of plate and stiffeners, the finial governing equation of stiffened plate is assembled by using compatibility conditions,which is used to ensure the compatibility of displacements at the interface between plate and stiffeners.Numercal results of the proposed method are compared with those obtained from finite element software MSC,and good agreements are achieved.In addition,a series of numerical analyses are conducted to further explore free vibration analysis of composite stiffened plate structure.Conclusion derived from this study is expected to be useful for stiffened plate structure aralysis.

dynamic substructure method;fixed-interface modal synthesis technique;stiffened plate;free vibration;composite material

TB332

：A

：1674－5590（2016）06－0038－05

2016-03-01；

：2016-03-31

国家自然科学基金青年基金（11502286）；中国民航大学“蓝天青年学者”培养计划（205003110307）；中国民航大学科研基金项目（2011kyE03）

钱若力（1959—），男，天津人，副教授，博士，研究方向为复合材料结构分析.