均衡问题的一种改进不精确次梯度算法

党亚峥, 沈 忱, 刘雯雯

(上海理工大学 管理学院,上海 200093)

均衡问题的一种改进不精确次梯度算法

党亚峥, 沈 忱, 刘雯雯

(上海理工大学 管理学院,上海 200093)

针对采用精确次梯度算法求解均衡问题中的稳固非扩张算子的不动点集问题(EP(f,Fix(T)))时计算复杂且收敛性较差这一情况,提出了一种改进的不精确次梯度算法.首先,由事先选择的参数确定一个凸集;其次,通过不精确次梯度投影算法构造中间迭代点;最后,将当前迭代点和中间迭代点的线性组合在稳固非扩张算子的映射作为下一次迭代点.在合适条件下验证了算法的全局收敛性.

均衡问题; 次梯度; 稳固非扩张映射; 全局收敛

1 问题描述

稳固非扩张算子的不动点集上的均衡问题[1](EP(f,Fix(T)))即找一个点

(1)

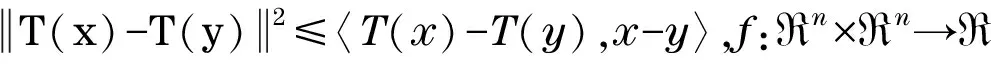
EP(f,Fix(T))问题是非空闭凸约束集中有关均衡问题的特殊类型,主要包括:最优化问题、纳什均衡问题、互补问题、不动点问题、变分问题及向量极小化问题等,其在码分多址联系方式(CDMA)[2]的系统能量控制问题和库洛特-纳什寡头市场均衡模型[3]中也有应用.文献[4-9]中提出了许多解决这类问题的迭代算法.近年来出现了很多求解问题(1)的改进次梯度投影算法[10-15].本文提出了求解稳固非扩张映射不动点集中均衡问题的一种新的有效的全局收敛算法.通过选择合适的正则参数,保证算法产生的序列全局收敛到EP(f,Fix(T))问题中的一个解.相对而言,本文提出的算法只需在每次迭代中作一次不精确的投影,比较容易实施.

2 预备知识

定义1 如果算子T满足

(2)

则称算子T非扩张.

PC表示从Rn到Rn上非空闭凸子集C的投影,则有

(3)

易知PC(x) 有如下性质:

〈x-PCx,z-PCx〉≤0, ∀z∈C,x∈Rn

(4)

故PC非扩张.

定义2 双函数f:C×C→R∪{+∞}.

a. 如果对每个x,y∈C,有

f(x,y)+f(y,x)≤0,则称f在子集C上是单调的.

b. 对于每个x,y∈C,有

f(x,y)≥0 ⟹f(y,x)≤0,则称f在子集C上是伪单调的.

定义3 双函数f在点x∈C处的ε次微分∂εf(x,·)(x)定义为

设E为巴拿赫空间,S是定义在E中的一个非空凸子集,E满足Opial性质[16],如果存在任意的序列{xk}都属于E,xk→x*,则

(5)

现使用引理1和引理2对算法进行收敛性分析.

引理2 非负实数θ,β满足不等式θ2-βθ≤0,则

(6)

证明 考虑二次函数s(θ)=θ2-βθ,当s(θ)≤0时,有

用β乘上面的不等式,即可得

证毕.

在收敛性分析中,假定式(1)的解集包含其对偶问题的解集,即

当x*∈Fix(T)时,有

(7)

这个问题的解集可以表示为Sd(f,Fix(T)).

函数f表示C上的伪单调双函数(如果x,y∈C和f(x,y)≥0,则可知f(y,x)≤0),有S(f,C)⊆Sd(f,C).这个结论对单调双函数也有效,即f(x,y)+f(y,x)≤0.

3 不精确次梯度算法及其全局收敛性

3.1 不精确次梯度算法

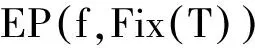
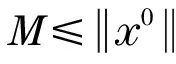
(8)

(9)

步骤2 计算

(10)

令k:=k+1,转步骤1.

(11)

3.2 收敛性分析

引理3 对任意k,下列不等式成立:

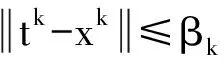
证明 由式tk=Pck(xk-αkgk)和式(4)得

(12)

由步骤1得

(13)

将x=xk代入式(12),由Cauchy-Schwarz不等式和式(13)可得

假设 A1S(f,C)的解集是非空的.

命题1 假设Sol(f,Fix(T))是非空的,则对任意的k,x*∈Sol(f,Fix(T)),下列不等式成立:

(15)

证明 显然

当x=x*时,由式(11)和式(13)可知

由Cauchy-Schwarz不等式及引理3的a可得

利用式(18)和引理3的b可得

2αk〈gk,x*-xk〉≤2αkf(xk,x*)+2αkεk

(20)

显然,由式(19)和式(20)可得式(15).

现证明在假设A1成立的情况下,由改进不精确次梯度算法生成的序列{xk}是有界的.

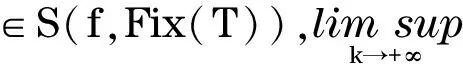
证明 对任意的x*∈Sol(f,Fix(T)),已知

由式xk+1=T(λkxk+(1-λk)tk),算子的非膨胀性和式(15)易知

由假设A1得f(xk,x*)≤0,由命题1可知

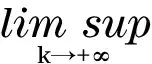
由命题1和假设A1可知

则

当m→+∞时,有

由参数的已知条件可知

(25)

利用参数定义可得

因此

(26)

所以,由式(25)和式(26)可知

(27)

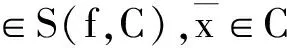
假设A3 当存在y∈C时,f(·,y)是上半连续的.

定理2 设C是在Rn上的非空闭凸子集,T:C→Rn表示一个稳固非扩张性映射,序列{gk}有界,若假设A1,A2,A3成立,令Fix(T)有界且其上界M>0,均衡函数f:Rn×Rn→Rn对于所有的x∈Rn满足f(x,x)=0,序列{gk}有界,则可知由算法1产生的序列{xk}收敛到EP(f,Fix(T))的一个解.

证明 设 x*∈S(f,C),由定理1易知,存在序列{xk}的子序列{xkj},满足

(28)

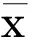
(29)

从假设A2和定理1可知

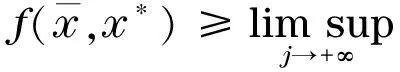
(30)

(31)

4 结 论

提出了一种求解均衡问题中关于稳固非扩张映射T上的不动点集问题的不精确次梯度迭代算法.通过选择适当的正则参数,验证不精确次梯度算法的全局收敛性.相对于精确次梯度算法,减少了计算工作量,同时提高了算法的收敛性.

[1] BLUM E,OETTLI W.From optimization and variational inequalities to equilibrium problems[J].Mathematics Student,1994,63(1):123-145.

[2] IIDUKA H,YAMADA I.An ergodic algorithm for the power-control games for CDMA data networks[J].Journal of Mathematical Modelling and Algorithms,2009,8(1):1-18.

[3] IIDUKA H.Fixed point optimization algorithm and its application to power control in CDMA data networks[J].Mathematical Programming,2012,133(1/2):227-242.

[4] ANH P N.A hybrid extragradient method extended to fixed point problems and equilibrium problems[J].Optimization:A Journal of Mathematical Programming and Operations Research,2013,62(2):271-283.

[5] ANH P N,KIM J K.Outer approximation algorithms for pseudomonotone equilibrium problems[J].Computers & Mathematics with Applications,2011,61(9):2588-2595.

[6] BIGI G,CASTELLANI M,PAPPALARDO M.A new solution method for equilibrium problems[J].Optimization Methods and Software,2009,24(6):895-911.

[7] NOOR M A.Auxiliary principle technique for equilibrium problems[J].Journal of Optimization Theory and Applications,2004,122(2):371-386.

[8] QUOC T D,ANH P N,MUU L D.Dual extragradient algorithms extended to equilibrium problems[J].Journal of Global Optimization,2012,52(1):139-159.

[9] 宇振盛,张丽娜,秦毅.非线性优化问题的光滑化序列二次规划方法[J].上海理工大学学报,2015,37(4):317-321.

[10] 陈元媛,高岩.一种非线性扩展混合共轭梯度算法的全局收敛性[J].上海理工大学学报,2013,35(2):113-115.

[11] NGUYEN T T V,STRODIOT J J,NGUYEN V H.A bundle method for solving equilibrium problems[J].Mathematical Programming,2009,116(1/2):529-552.

[12] TRAN D Q,DUNG L M,NGUYEN V H.Extragradient algorithms extended to equilibrium problems[J].Optimization,2008,57(6):749-776.[13] VAN NGUYEN T T,STRODIOT J J,NGUYEN V H.The interior proximal extragradient method for solving equilibrium problems[J].Journal of Global Optimization,2009,44(2):175-192.[14] IIDUKA H,YAMADA I.A subgradient-type method for the equilibrium problem over the fixed point set and its applications[J].Optimization,2009,58(2):251-261.

[15] SANTOS P,SCHEIMBERG S.An inexact subgradient algorithm for equilibrium problems[J].Computational & Applied Mathematics,2011,30(1):91-107.

[16] OPIAL Z.Weak convergence of the sequence of successive approximations for nonexpansive mappings[J].Bulletin of the American Mathematical Society,1967,73(4):591-597.

[17] CROMBEZ G.A geometrical look at iterative methods for operators with fixed points[J].Numerical Functional Analysis and Optimization,2005,26(2):157-175.

(编辑:石 瑛)

Improved Subgradient Algorithm for Equalization Problems

DANG Yazheng, SHEN Chen, LIU Wengweng

(BusinessSchool,UniversityofShanghaiforScienceandTechnology,Shanghai200093,China)

The exact subgradient algorithm for solving the equilibrium problem (EP(f,Fix(T))) of sets over the fixed point of non-expansive operator causes computational complexity and poor convergence.To overcome the defect,an inexact subgradient algorithm for theEP(f,Fix(T)) was presented.A convex set assured by given parameter was selected,the intermediate iterative point was constructed by using the non-accurate subgradient projection algorithm and the image,under firmly non-expansive operator of the linear combination of the current iterative point and middle iterative point was taken as the next iteration point.Under suitable conditions,the global convergence of the algorithm was verified.

equilibriumproblem;sub-gradient;firmlynon-expansivemapping;globalconvergence

1007-6735(2016)06-0523-04

10.13255/j.cnki.jusst.2016.06.003

2016-04-01

上海市自然科学基金资助项目(14ZR1429200);上海市教育委员会科研创新项目(15ZZ073)

党亚峥(1973-),女,副教授. 研究方向:可行问题、均衡问题、智能电网电力市场.E-mail:jgdyz@163.com

O 221

A