基于剩余能量的无线传感器网络功率控制非合作博弈

◆李翔宇

（闽江师范高等专科学校 福建 350007）

基于剩余能量的无线传感器网络功率控制非合作博弈

◆李翔宇

（闽江师范高等专科学校 福建 350007）

本文提出了一个基于剩余能量的无线传感器网络功率控制非合作博弈。每个节点可以自主选择功率控制策略以实现自身传输能量效率的最大化。由于传感器网络中节点能量总是有限的，我们将一个与剩余能量有关的参数引入到效用函数中。该博弈可以被证明存在唯一纳什均衡。数值仿真分析验证了该模型的有效性，并且数值分析结果显示当考虑到节点的剩余能量时，网络的生存性有所提高。

无线传感器网络；功率控制；剩余能量；非合作博弈

0 引言

无线近年来越来越多致力于研究通过提高终端主机、数据中心以及云的能量有效性来设计更加绿色的网络基础设施的研究[1]。由于能量有限，很有必要在QoS和能量消耗之间寻求某种权衡，形成更加节能和绿色的传感器网络，这也与近年来所提的设计更加绿色的网络基础设施[1]的思想相适应。运用文献[2]中给出的能量有效性效用函数来衡量一个通信的能量有效性的程度是一个很常见的方法，将消耗单位能量能够成功传输的比特信息数定义为能量有效性。该文中，博弈中的参与者为网络中的发送者，他们自私的寻求最大化自身效用函数的策略。文献[3]中，将[2]中的结论推广到多载波系统。由于[1]中的纳什均衡有效性不佳，已经有许多其他的博弈理论概念被用来提高均衡的有效性，如：在文献[4]中给出了一个价格机制，该机制具有帕累托最优均衡，但是，该机制需要全局信道信息。文献[6]则提出了一个分层次的Stackelberg博弈，该博弈中仅需要个人信道信息，但得到的均衡不是帕累托最优的。在[7]中，基于TDMA-CDMA的分簇的无线传感器网络中的各个簇中的上行通信被抽象为Stackelberg功率控制博弈。他们将节点的剩余能量引入到效用函数中，并且通过实验说明了当考虑到剩余能量时，网络的生存时间确实能够延长。此前，比较少的文献在能量有效性问题中考虑节点的剩余能量，但在文献[7]中有提到。

1 系统模型

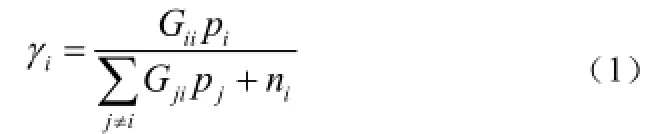
定义1 非合作功率控制博弈：非合作功率控制博弈是一个组合，其中N是参与者集合，是参与者i的策略集，iu为参与者i的效用函数，定义为：

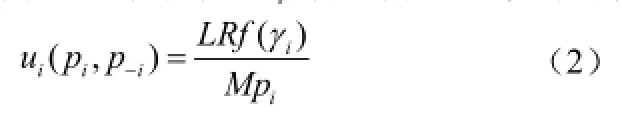
其中，ip-代表除了参与者i以外的其他参与者的策略，；L是当使用发送功率ip并且发送速率为时，发送的数据包大小为ML＞的数据包中的信息比特数[10]。另外，为了方便，我们假设发送速率R为固定值；为有效性函数，定义为：

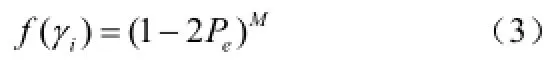
其中，eP为误码率（Bit Error Rate，BER）。

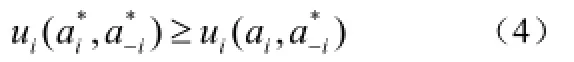
则称*a为博弈G的一个纳什均衡。

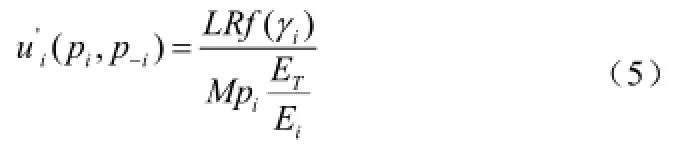
其中，TE和iE分别代表节点的总能量和剩余能量。将参数引入到效用函数的分母中是出于以下原因：当剩余能量越大时，参数的值就越小时则为最小值1），此时不论选择什么发送功率对效用函数的影响都很小。但是，当剩余能量越小时，将会越大，如果此时用户继续使用一个很大的功率来发送数据，则会变得更大，这将会使得自身的效用函数值下降的更快，因为效用函数与成反比。因此，我们引入以达到当剩余能量少的时候能够促使节点使用更小的功率来发送数据的目的。

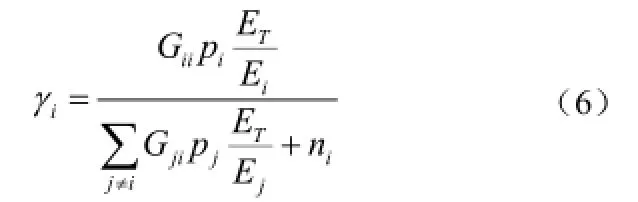
因此，我们可以得到引入剩余能量后的非合作功率控制博弈为组合：。接着，我们定义考虑剩余能量的非合作功率博弈的纳什均衡。

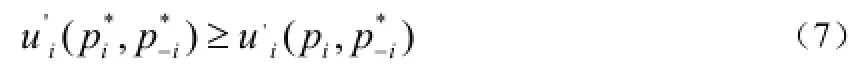
在下一节中，我们将会分析该博弈纳什均衡的存在性和唯一性。

2 均衡分析

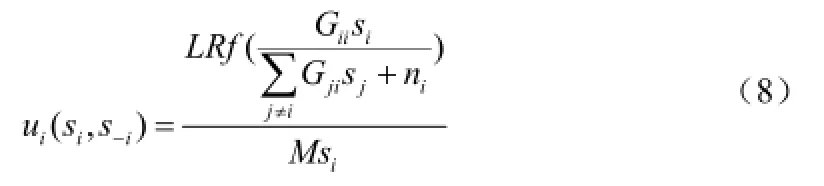
通过观察参数变换后的效用函数，可以发现剩余能量和信道增益只在节点反计算自身发送功率，即时需要用到，这表明：进行该博弈只需要知道节点自身的信道信息以及剩余能量信息。通过参数变换，可以利用已有的结论来分析该博弈的均衡存在性。

定理1 有以下效用函数形式的能量有效性功率控制博弈：

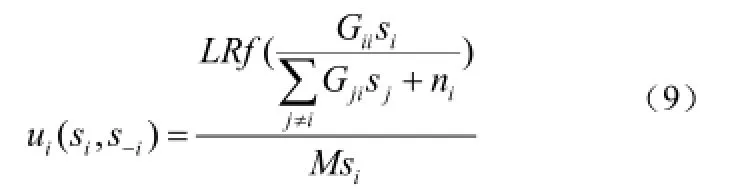
定理1的详细证明可以参照文献[11]。本文将重点放在说明该定理如何适用于文中的考虑剩余能量的非合作功率控制博弈。

在定理1中给出的均衡（10）在信号噪声比上，对所有用户是公平的，因为该均衡给出的是对各个节点而言要达到的信噪比值。回到考虑剩余能量的情形，在参数变换之后，得到一个形如（10）的纳什均衡，而得到考虑剩余能量的功率博弈的纳什均衡只需要计算：

参考[13]，在考虑剩余能量时，达到均衡对终端的数量N的限制条件，即当时，所有节点都能够达到均衡时的信噪比要求。（10）中给出的纳什均衡具有的一个重要特性就是：每个用户只需要知道自己的信道增益信息来选择均衡策略。相应的在考虑剩余能量是的纳什均衡（11）中，唯一增加的条件就是需要知道自身的剩余能量值。因此，只需要个人的信道及剩余能量信息，就可以分布式的实施该功率控制，而不需要公共信号，这能够很好的适应无线网络的实际情形非常符合。

3 数值分析实验

本章通过MATLAB数值仿真实验分析来验证文中所给出的考虑剩余能量的功率控制博弈的性能。考虑一个简单的CDMA系统。每个节点的发送功率假定可以是中的任意值，其他参数假设为：，并且节点使用非相干FSK调制技术，则误码率为。因此效用函数可表示为：。通过对（8）标准化效用函数求导，得到和。这表示，如果发送者的数量少于或等于9，所有发送者都可以达到。

考虑一个只有两个用户的系统：1user以及2user。用该系统来说明随着功率的变化所能够得到的效用值。假设当前1user和的剩余能量情况为：。通过计算：

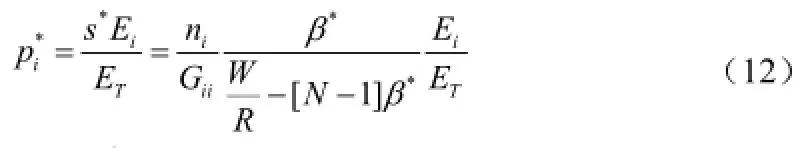
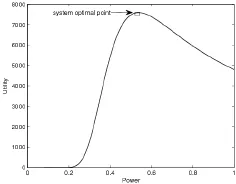
图1 用户1的效用函数

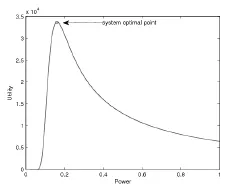
图2 用户2的效用函数

考虑当有8个发送者的情形，信道增益假定为：

表1给出引入剩余能量到效用函数中与没有引入时的节点生存时间对比。可以看出，将剩余能量引入到效用函数后，有效延长了节点的生存时间。

表1 收益函数改进前后节点的寿命比较

4 小结

在本文为设计更加绿色的无线传感器网络，提高网络的生存性，对节点进行功率控制并考虑节点的剩余能量来提高能量使用的有效性和提高节点的生存性。将考虑剩余能量的功率控制问题抽象为一个非合作博弈模型，并将节点的剩余能量以参数的形式引入到博弈中节点的效用函数中。通过参数变换，可以证明该博弈具有唯一的纳什均衡，并且节点只需要知道自身的信道和剩余能量信息就可以实施功率控制过程。数值仿真分析验证了模型的有效性，并且验证了通过将剩余能量引入到效用函数中，确实能够提高节点的生存性。

[1] F．Meshkati，M．Chiang，H．V．Poor and S．C．Schwartz．A game-theoretic Approach to Energy-efficient Power Control in Multi-carrier CDMA systems．CoRR abs/cs/0512014（2005）．

[2] David Goodman，and Narayan Mandayam．Power Control for Wireless Data[J]．IEEE Journal on Selected Areas in Communications（JSAC），2001．

[3] Yezekayel Hayel，Majed Haddad．Hierarchy induces Spectrum Coordination in Energy Efficient Multi-carrier Power Control Game．CoRR abs，2012．

[4] S．M．Perlaza，E．V．Belmega，S．Lasaulce，and M．Debbah．On the Base Station Selection and Base Station Sharing in Self-Configuring Networks[C]．ValueTools 09：Proceedings of the 4th International Conference on Performance Evaluation Methodologies and Tools，2009．

[5] P．T．V．Bhuvaneswari，Vijay Vaidehi，M．Agnes Saranya．Distance Based Transmission Power Control Scheme for Indoor Wireless Sensor Network[J]．Transactions on Computational Science（TCOS），2010．

[6] Fu-Yun Tsuo，Hwee-Pink Tan，Yong Huat Chew，Hung-Yu Wei．Energy-Aware Transmission Control for Wireless Sensor Networks Powered by Ambient Energy Harvesting：A Game-Theoretic Approach．ICC 2011．

[7] Seyed Mohammad Mahdi Alavi，Michael J．Walsh，Martin J．Hayes．Robust Power Control for IEEE 802．15．4 Wireless Sensor Networks with Round-trip Time-delay Uncertainty[J]．Wireless Communications and Mobile Computing（WICOMM），2010．

[8] Dimitris E．Charilas，Athanasios D．Panagopoulos．A Survey on Game Theory Applications in Wireless Networks [J]．Computer Networks，2010．

[9] Shrutivandana Sharma，Demosthenis Teneketzis．A Game-theoretic Approach to Decentralized Optimal Power Allocation for Cellular Networks[J]．Telecommunication Systems（TELSYS），2011．

[10] Tao Shu，Marwan Krunz．Energy-efficient Power/rate Control and Scheduling in Hybrid TDMA/CDMA Wireless Sensor Networks[J]．Computer Networks，2009．

[11] Beibei Wang，Yongle Wu，and K．J．Ray Liu．Game Theory for Cognitive Radio Networks：An overview[J]．Computer Networks（CN），2010．

[12] Mahir Meghji，Daryoush Habibi．Transmission Power Control in Single-Hop and Multi-hop Wireless Sensor Networks[C]．MACOM，2011．

[13] Juan Luo，Pan Chen，Renfa Li，Fei Ge．Power Control in Distributed Wireless Sensor Networks Based on Noncooperative Game Theory[J]．IJDSN，2012．