巧妙换元 奇妙简证一类无理型不等式

浙江省湖州市双林中学

李建潮 (邮编：6313012)



巧妙换元 奇妙简证一类无理型不等式

浙江省湖州市双林中学

李建潮 (邮编：6313012)

文[1]提出了如下两个有趣的无理型不等式猜想:

设a、b、c是满足abc=1的正数，则

①

②

文[2]证明了这一猜想,并于文末提出如下一般性问题:

若a、b、c是满足abc=1的正数，则使不等式:

③

成立的最佳常数λ是多少?

文[3]发现对λ≥0,③式恒成立,即文[3]建立并证明了如下不等式:

设a、b、c∈R+,且abc=1,λ≥0,则

④

但唯一的缺憾是文[3]的证明过程过于冗长,影响了可读性.出于“数学的本质往往是最简单的”的考虑,笔者改进文[3]的换元角度,让④式的证明趋于更合理、更明快.

事实上，如若对④式作如下换元：令

则xyz=abc=1，并从中反解出：

(*)

代入④，可化为

所以,④式等价于如下不等式：

设x、y、z∈R+,且xyz=1,λ≥0,则

⑤

以下证明⑤式：

其次,利用三维柯西(Cauchy)不等式：

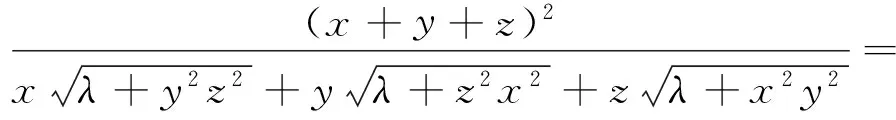
所以，⑤式获证，即④式得证.

设a、b、c∈R+,且abc=1,λ≥0,则

⑥

设a,b,c∈R+,则

⑦

评注 文[3]在证明④式时选择了前一种代换,转而把证明④式归结为证明⑥式,而这种代换对证明⑥式绝非是一桩易事.证明不等式往往就“差”在那么一点技巧性上,而这又恰恰是不等式证明的一个显著特点，特别是数学竞赛与初数研究.

1 宋庆.关于一些不等式的研究与讨论[J].中学数学研究(江西),2012(12)

2 吴裕东.一对无理不等式猜想的证明[J].不等式研究通讯,2013(1)

3 汪长银.两道猜想不等式命题的统一推广[J].数学通讯(下半月),2014(7)

2016-09-28)