模糊参数软集

高德宝，朱 焕

（黑龙江八一农垦大学 理学院，黑龙江 大庆 163319）

模糊参数软集

高德宝，朱 焕

（黑龙江八一农垦大学 理学院，黑龙江 大庆 163319）

模糊参数软集是利用模糊参数集研究模糊软集的理论。它为处理模糊目标提供了一个新的工具。本文引入模糊参数软集的基本概念，给出模糊参数软集的一些运算并讨论了与运算有关的一些性质。

模糊集；软集；关系函数；模糊参数软集；运算

在生物学、经济学、环境与工程学、医学等许多领域，有许多具有不确定性、模糊性和无法清晰定义目标的复杂问题。有三种理论：概率论、区间数学和模糊数学被用来处理这样的问题。Molodstov[1]指出这些理论都有他们自己本身的缺陷并引入了软集理论来克服这些缺陷。2003年，Maji[2]等人在软集中引入了一些代数运算并对软集做了更细致的研究。从此以后，许多学者[3-5]致力于软集代数结构的研究。不过，文[6]的结果表明软集运算实际上就是布尔矩阵的运算。Maji[7]等人基于软集理论与模糊集理论提出了模糊软集理论。他定义了模糊软集的并、交和补的概念。Ahmad[8]等人修正了Maji的模糊软集交的定义并更一步的研究了模糊软集的运算。近几年，许多学者[9-12]致力于软集运算的研究。

在本文中，我们定义了模糊参数软集及其运算的基本定义，并用实例表明其实用性。本文的主要内容可以说是模糊软集理论的进一步的研究。

1 预备知识

在这一节，我们主要回忆一些基本的概念，如模糊集、软集和模糊软集等。然后，我们修正模糊软集的概念。在本文的全文中，U是指一个原始的事物集，E是事物集U的参数集，P(U)是U的幂集。

模糊集的概念在文[13]中是按如下方式给出的。

定义1集合U中的一个模糊集F是由它的隶属函数F(u)所刻画的。对于U中的任一点u，均有一实数与之对应，实数值F(u)代表着u在F中的隶属程度。

一个集合U上的模糊集F可以按下面的方式表示：

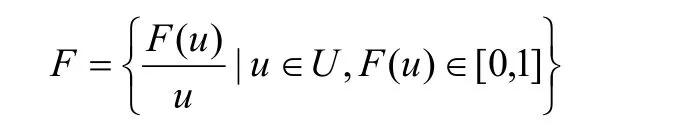
注：集合U上的所有模糊集用F(U)来表示。

定义2[1]一对有序组合(G,E)被称作集合U上的一个软集当且仅当G是一个E到P(U)的一个映射。

一个集合U上的软集(G,E)可以用下面的两类有序对的集合来表示。

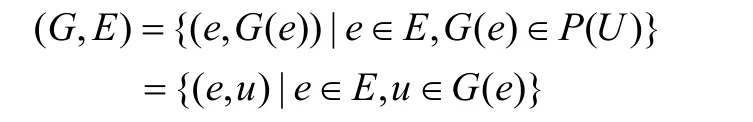
定义3软集(G,E)的关系函数RGE的定义如下：

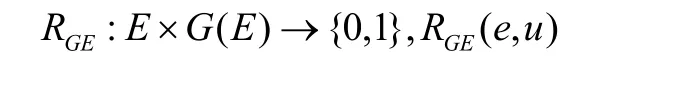
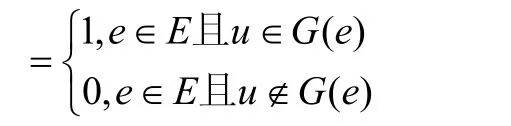
容易知道软集(G,E)与它的关系函数RGE具有一一对应关系。因此，我用关系函数RGE来标识软集(G,E)。

例1设U={h1,h2,h3,h4,h5}是五个房子的集合。设参数集E={blackish, reddish, green, large}且软集(G,A)可以写作

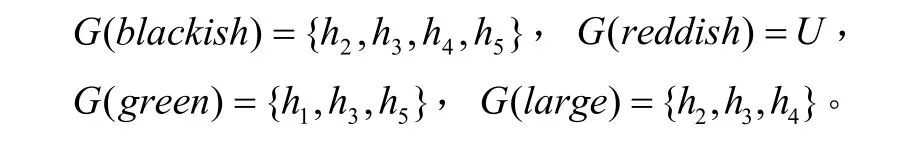
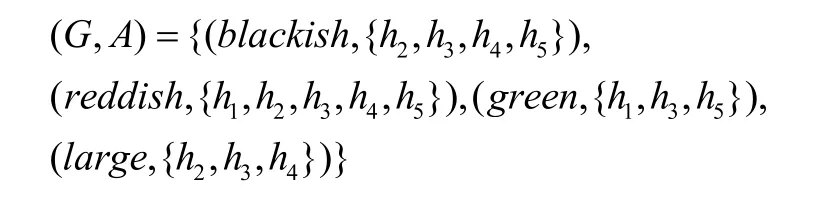
利用关系函数RGE，我们也可以用表格与矩阵来表示软集(G,A)。

Maji[7]对模糊软集的定义如下：

定义4一对组合(f,A)(A⊆E)被称为U上的模糊软集当且仅当f:A→F(U)是一个从A到F(U)的映射。

这里，对于任意的e∈A，f(e)必然是一个模糊集合，其隶属函数记为fe，为表示的方便性，我们将f(e)也记为fe。

例2假设一个模糊软集(f,A)描述了五件待售衬衫U={x1,x2,x3,x4,x5}对顾客的吸引力。描述衬衫特征的集合是

在上例中，很容易知道模糊集f(e5)=φ。它意味着因此，我们可以按如下的方式修正模糊软集。

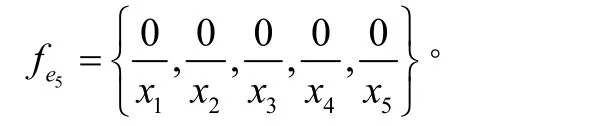
定义5一对组合(f,E)被称为U上的模糊软集当且仅当f:E→F(U)是一个从E到F(U)的映射。

一个U上的模糊软集可以用下面的有序对来表示：

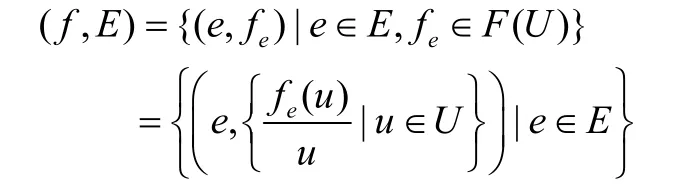
这里，fe(u)是u属于fe的程度或者是函数fe在集合U上的隶属函数值，fe(u)被称为e和u的模糊关联度。

2 模糊参数软集

为引入本文的核心定义，我们考虑下面一个案例的数学描述。

例3假设某一公司想要补充某一工作岗位。有5名候选人填表申请该岗位。设候选集

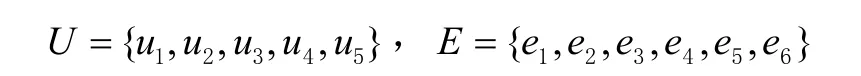
是一个参数集。参数ei( i=1,2,L,6)分别代表“有经验”、“电脑知识丰富”、“受过训练”、“年轻”、“高学历”和“身体健康”。人力资源经理给集合E中的每个元素一个权。可以说，这个经理构建了一个E上的模糊集

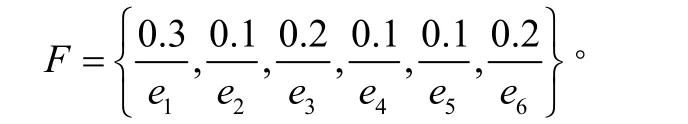
来自执行董事会的决策者根据参数集U上的元素对候选人建立如下的模糊软集：

为了更全面的表述F与(f,E)之间的关系，我们给出如下的定义：

定义6设U={u1,u2,Λ,um}是一个原始的事物集，E={e1,e2,Λ,en}是一个参数集，F是集合E上的一个模糊集，(f,E)是集合U上的一个模糊软集。那么集合E与U上的一个模糊参数软集Ff定义如下：

Ff={(e,F(e),fe(u))|(e,u)∈E×U}。

这里，F (e)·fe(u)是(e,u)属于Ff的隶属程度或模糊软参数软集Ff的隶属函数。本文把集合E和U上所有模糊参数软集记为FPS(E,U)。

根据定义3很容易证明下面结论的正确性。

性质1设Ff∈FPS (E,U)，那么∀(e,u )∈E×U，有0≤F( e)·fe( u )≤1。

定义7设Ff∈FPS(E,U)，如果对于任意的(e,u)∈E×U ，有F(e)=0且fe(u)=0，那么称Ff是一个空模糊参数软集，记作Φ。如果对于任意的(e,u)∈E ×U，有F(e)·fe(u)=1，那么称Ff是一个全

类似地，对于任意的

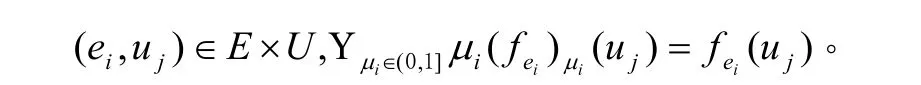
从而有结论（1）成立，同样的方式结论（2）成立。定义16设

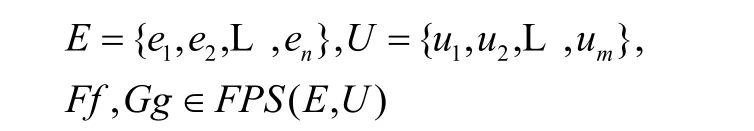
“Ff且Gg”是一个模糊参数软集，记作Ff∧Gg，这里

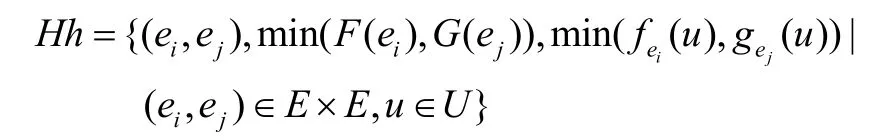
“Ff与Gg”是一个模糊参数软集，记作Ff∨Gg，这里

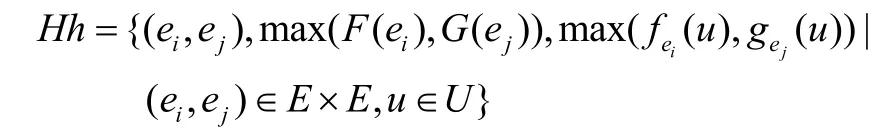
下面的一些结论根据定义16是很容易证明，故这里我们不给予证明，仅给出结论。

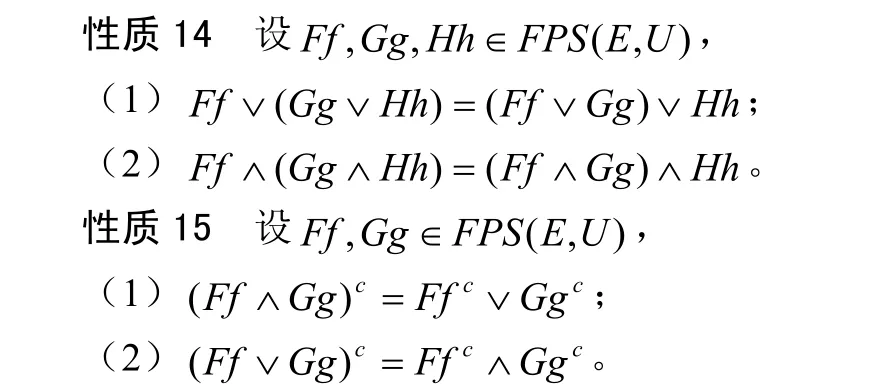
证明（1）与（2）的证明类似，这里仅证明（1）。设Ff∧Gg=Hh 。则有

3 结论

本文给出了模糊参数软集的概念。它可以看作是基于模糊软集而推广的模糊集。文中定义了模糊参数软集的一些运算，并用对他们进行了解释。这些运算还具有一些代数性质，我们也挖掘了一部分，相信还会有一些比较有用的性质有待探索。

[1] Molodtsov D. Soft set theory-First results[J]. Computers and Mathematics with Applications, 1999, 37(4-5): 19-31.

[2] Maji P K, R Biswas, A R Roy. Soft set theory[J]. Computers and Mathematics with Applications, 2003, 5(4-5): 555-562.

[3] Sezgin A, Atagun A O. On operations of soft sets[J]. Computers and Mathematics with Applications, 2011, 61(5): 1457-1467.

[4] Ali M I, Feng F, etc. On some new operations in soft set theory[J]. Computers and Mathematics with Applications, 2009, 57(9):1547-1553.

[5] Ali M I, Shabir M, Naz M. Algebraic structures of soft sets associated with new operations[J]. Computers and Mathematics with Applications, 2011, 61(9): 2647-2654.

[6] Cagman N, Enginoglu S. Soft matrix theory and its decision making[J]. Computers and Mathematics with Applications, 2010, 59(10):3308-3314.

[7] Maji P K, Biswas R and Roy A R. Fuzzy soft sets[J]. Journal of Fuzzy Mathemtatics, 2001, 9(3): 589-602.

[8] Ahmad B and Kharal A. On fuzzy soft sets[J]. Advances in Fuzzy Systems, 2009, 2009: 1-6.

[9] Cagman N, Enginoglu S and Citak F. Fuzzy soft set theory and its applications[J]. Iranian Journal of Fuzzy systems, 2011, 8(3):137-147.

[10] Neog T J, Sut D K. On union and intersection of fuzzy soft set[J]. International Journal of Computer Technology and Applications, 2011, 2(5): 1160-1176.

[11] Ali M I. A note on soft sets-rough soft sets and fuzzy soft sets[J]. Applied Soft Computing, 2011, 11(4): 3329-3332.

[12] Basu T M, Mahapatra N K and Mondal S K. On some new operations in fuzzy soft set and intuituionistic fuzzy soft set theory[J]. International Journal of Computer Science and Information Technology and Security, 2012, 2(2): 408-417.

[13] Zadeh L A. Fuzzy sets[J]. Information and Control, 1965, 8(3): 338-353.

（责任编辑、校对：赵光峰）

Soft Set with Fuzzy Parameter

GAO De-bao, ZHU Huan
(College of Sciences, Heilongjiang Bayi Agricultural University, Daqing 163319, China)

The fuzzy parameter soft set is the theory of fuzzy soft sets with fuzzy parameters set and offers a new mathematical tool for dealing with fuzzy objects. The main purpose of this paper is to introduce the basic notions of the fuzzy parameter soft set, to present some operations of the sets, and to discuss some properties associated with the fuzzy parameter soft set operation.

Fuzzy set; Soft set; Relation function; Fuzzy parameter soft set; Operation

O159

A

1009-9115(2016)02-0005-06

10.3969/j.issn.1009-9115.2016.02.002

大庆市科技计划项目（szdfy-2015-47）

2015-12-13

高德宝（1975-），男，黑龙江大庆人，硕士，讲师，研究方向为数学分析、运筹与决策。