干耦合超声波激励信号研究
2016-02-07艾春安蔡笑风刘凯旋
艾春安,蔡笑风,李 剑,刘凯旋
(火箭军工程大学,陕西 西安 710025)
干耦合超声波激励信号研究
艾春安,蔡笑风,李 剑,刘凯旋
(火箭军工程大学,陕西 西安 710025)
为保证干耦合超声波探头的正常工作,采用理论分析与实验相结合的方法对其激励信号进行选择。干耦合超声波探头与试件直接接触,入射能量低,不同粘接状况下接收信号能量(E)差异较大,品质因数(Q)能够表征接收信号的带宽及强度分布,两者可作为激励信号的选择依据。根据各信号表达式分别采用方波、锯齿波及高斯窗、海明窗和汉宁窗调制的正弦脉冲信号进行试验。试验结果表明:在重复频率和电压幅值不变的条件下,对于玻璃纤维/丁腈橡胶复合材料粘接板,最优激励波形为5周期汉宁窗调制正弦波脉冲信号,激励频率约为100kHz,为干耦合超声波探头的检测应用提供基础。
干耦合;超声波激励;窗函数;品质因数
0 引 言
在常规超声波检测过程中,为了实现声能从探头向试件的有效传递,通常用到水、甘油或机油等耦合剂。虽然它们无明显腐蚀作用,但是对于固体火箭发动机壳体、飞机机翼等一些对结构完整性要求较高且需要长期使用或贮存的部件,使用耦合剂仍会造成一定的沾染,影响材料的物理和化学性能,破坏结构的完整性,因此需要寻求一种无需耦合剂(干耦合)的检测方法对这些结构进行超声波无损检测。
目前,国内关于干耦合超声检测的研究报道较少,郑海平等[1]对非金属复合材料干耦合超声自动探伤方法进行研究,分析了耦合压力、步距、转速对实验结果的影响;穆洪彬等[2]将干耦合超声检测技术应用于某火箭发动机喷管的在役检测中,对检测灵敏度进行了论述,得出能够检测10mm以上脱粘、分层、弱粘接缺陷的结论;周正干等[3-4]利用空气耦合超声检测技术,对纤维增强复合材料进行检测和评价,取得良好应用效果。美国西北大学Komsky[5-6]为了克服传统超声检测需要使用液体或胶状耦合剂的缺点,研制出一种应用于航空器结构检测的超声干耦合探头,该探头前端使用了聚合物薄层,与试件干耦合接触,在低压力情况下可适应各种不规则检测表面,可发射和接收MHz频带范围内的纵波和横波。法国蒙彼利埃大学Jimmy Duwattez等[7]研制出一种10~100MHz的高频干耦合探头,用来在微观尺度下对材料表面粗糙度和摩擦性能进行检测,其中延迟块用来在发射表面产生均匀的波形,它的长度必须大于或等于菲涅耳距离。英国布里斯托大学A.M. Robinson等[8]研制了一种低频(<500 kHz)干耦合轮式探头,并用于三层粘接结构的检测。英国华威大学C.E.Dixon等[9]在探头的前端设计了一定厚度的干耦合剂层,并用来与金属试件直接接触,并通过实验分析了不同厚度干耦合剂层对检测效果的影响。德国斯图加特大学Igor Solodov等[10]针对传统空气耦合超声检测空气-固体界面易出现阻抗不匹配的问题,提出了空气耦合Lamb波检测方法,并通过实验验证了该方法不仅能精确测量出复合材料内部纤维方向,还能对各向异性复合材料板中的裂纹和分层缺陷进行量化检测。日本川嶋紘一郎等[11-12]利用一种内置增幅80dB的高功率超声波发射接收器JPR-600,对复合材料内部缺陷进行损伤成像检测,实现了空气耦合超声波检测技术的实际应用。通过以上分析发现,各干耦合探头在与试件接触端采用了聚合物薄层、延迟块或干耦合剂层等特殊处理,设计制作难度较大;而空气耦合超声虽然同样不需要耦合介质,但是由于进入被检测材料内的超声波能量低、振幅小、衰减大,要求空气耦合探头具有低频、高灵敏度等特点,还需选择合适的带通滤波前置放大器,将接收信号增幅。目前国内没有自主生产的无需耦合介质的超声波检测设备,本文设计了一种传声杆形式的干耦合探头,并对其激励信号展开研究。
1 干耦合超声波检测
干耦合超声波检测由于耦合方式不同,所使用的探头与常规超声探头不同,其结构主要包括压电陶瓷振子、变幅杆、匹配电路和外部工装。探头的核心部件是三叠片压电陶瓷振子,该振子中间为金属圆盘,两边为压电陶瓷片,这种结构可明显改善探头的机械和机电耦合性能。外加电场方向与一个压电陶瓷圆片极化方向相同,而与另一个圆片的极化方向相反,当振子受外场激励时,一个圆片产生伸张效应,另一个产生收缩应变,结果就使整个双层圆片发生弯曲应变[13]。构建的干耦合超声检测系统硬件主要有:泰克AFG3052C型任意信号发生器、NF公司HSA4051型双极性功率放大器(最大输出电压为300Vp-p)及RIGOL公司MSO1104型四通道示波器。
检测时,两探头置于试件缺陷区域的两侧,并通过相同质量块进行加压固定,使探头中压电陶瓷片、前端变幅杆及被检测试件之间接触良好。该方法采用双探头一发一收检测方式,发射探头产生的超声波经被检测材料被接收探头接收,并在示波器上显示,根据接收信号幅值、能量及频谱等参数对缺陷进行定征。
干耦合探头前端使用了细长的变幅杆,和结构近似于点接触,这种接触方式势将会使超声波的入射效率大为降低,而且造成严重的能量损失,主要包括能量的衰减和能量的泄露两种。
单层薄板结构中Lamb波主要在上下表面之间传播,假设板的厚度保持不变,超声波能量的衰减由传播距离L决定[14],其表达式为

式中:QL——超声波传播距离L后声强;
Q0——超声波初始声强;
α——超声波衰减系数。
在多层结构的粘接界面处会发生能量泄露,即部分超声波会经粘接界面由一种材料进入到另一种材料,能量泄露的多少与粘接界面面积相关,粘接界面面积越大,能量泄露越多,其示意图如图1所示。超声波经过长度为x、宽度为1的粘接界面,泄露后能量为

式中:Qx——能量泄露后超声波声强;
β——超声波泄露系数。
超声波经由发射点T传播至接收点R,若粘接界面无缺陷,其能量关系式为

若粘接界面上存在脱粘缺陷,假设脱粘长度为b,则关系式为


图1 能量泄露示意图
当脱粘长度b大于换能器之间距离L时,取b=L。
假设完全脱粘、部分脱粘及粘接完好3种情况下接收点R处的能量分别为E1、E2及E3,由式(4)可知,接收点R处能量泄露随脱粘长度减小而降低,可得:E1>E2>E3。因此通过接收点R处能量的大小就可对粘接结构中是否存在缺陷进行判断。
2 试验验证
激励波形不同,检测过程中激发的超声Lamb波频带带宽和周期数不同,而这些都是影响损伤检测的重要因素。
检测试件为复合材料粘接结构,上层为S-2玻璃纤维板,下层为丁腈橡胶配方,在纤维板和橡胶的粘接界面上预置了一个聚四氟乙烯薄膜模拟空气夹层脱粘缺陷,试件大小为250mm×250mm,玻璃纤维板厚5mm,橡胶厚2mm,圆形区域为粘接界面上的脱粘缺陷,其大小为60 mm×50 mm,两探头相距约70mm。
2.1 不同激励波形的试验
方波是利用上升沿和下降沿来激励的,相当于探头受到两次激励,产生两个超声波,调节方波的宽度可以使两次激励的波形相叠加或相减,从而得到探头的最佳灵敏度或最佳分辨率。通常通过调节脉冲宽度来得到最佳的灵敏度,当脉冲宽度接近探头中心频率的1/2周期时,经常能够得到换能器的最佳灵敏度也就是信号的峰值。
外加激励的锯齿波可表示为
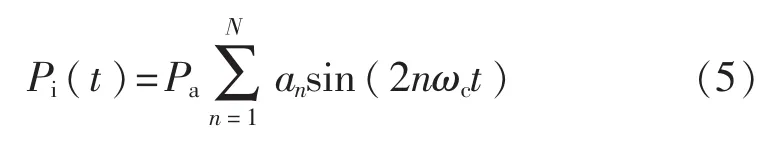
式中:an=(-1)n+1/(nπ);
ωc——信号基频;
P——信号幅度;
N——谐波数目,由于换能器的带宽限制,取N=2。
当复合材料粘接板中Lamb波传播一段距离后,由于它的频散及多模式特性,导致检测信号的成分比较复杂,给分析带来一定难度。而将激励信号的频率限制在一定的窄频段范围内能有效抑制频散。通常所用的激励波形多为用窗函数对正弦信号调制后得到的信号[15],可表示为
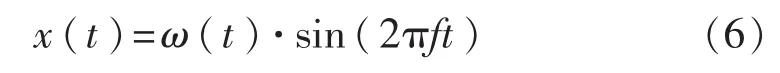
式中:ω(t)——调制用的窗函数;
f——激励信号的频率。
常用的窗函数有高斯窗、海明窗和汉宁窗等,其表达式分别为
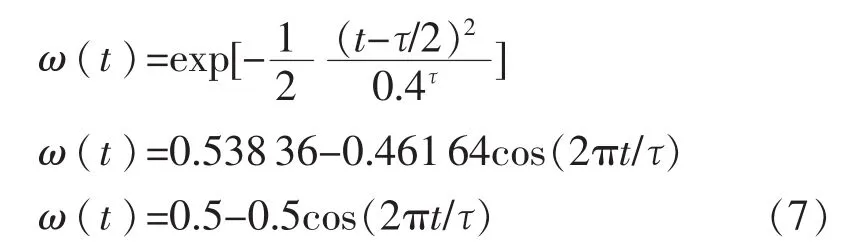
其中0≤t≤τ,τ=n/f,n为波数。
试验时,首先在PC机上根据以上表达式调制出各激励信号,发送至信号发生器,将输出阻抗设为高阻600Ω,重复频率为1kHz,幅值为2Vp-p,并通过功率放大器(放大倍数为20)将信号输出在发射探头上。激励波形为方波、锯齿波及高斯窗、海明窗和汉宁窗调制正弦波时的检测结果分别如图2~图6所示。
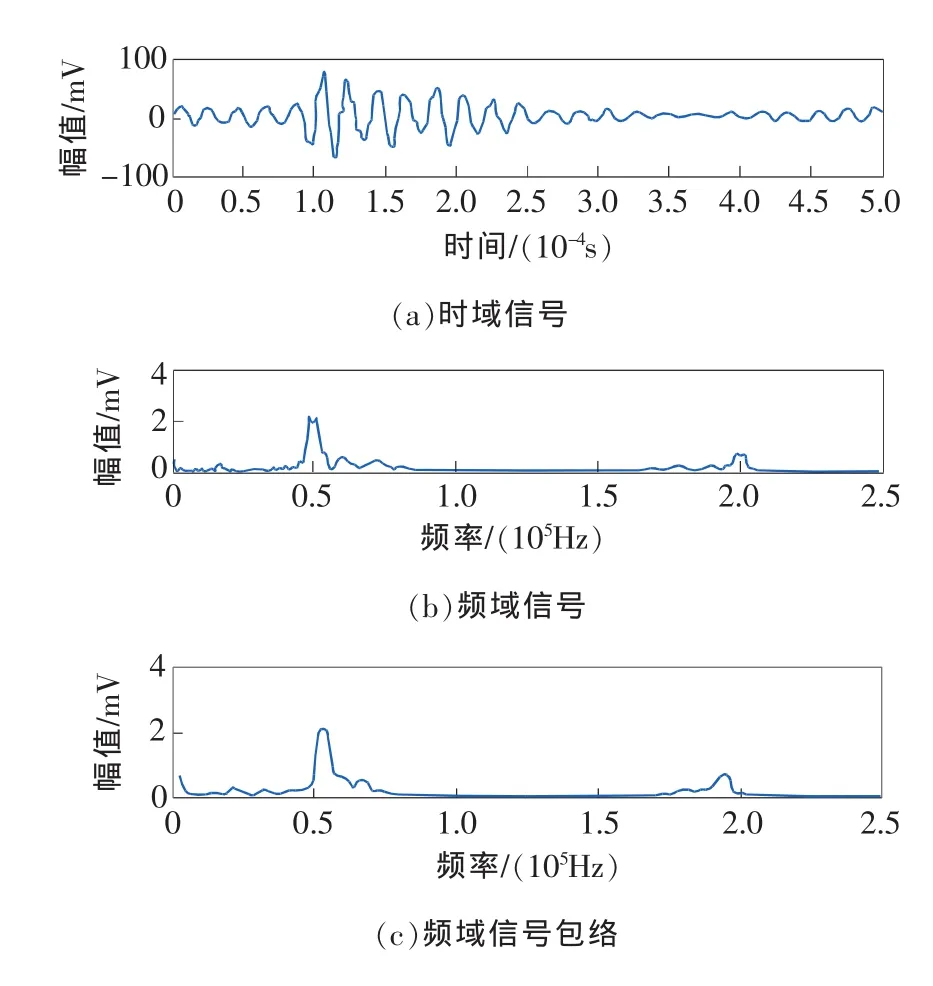
图2 方波检测结果

图3 锯齿波检测结果

图4 高斯窗调制正弦波检测结果

图5 海明窗调制正弦波检测结果

图6 汉宁窗调制正弦波检测结果
2.2 不同激励频率的试验
由于压电陶瓷片是一个弹性体,因此存在谐振频率。当外界作用的频率等于谐振频率时,压电陶瓷片就产生机械谐振,谐振时振子的振幅最大,弹性能量也最大。经测定,本文探头中单个压电陶瓷片的谐振频率约为70 kHz,但由于压电振子采用了三叠片结构,而且探头结构中加入了弹簧、紧固件等工装,实际的谐振频率需通过试验进行确定,选择激励频率分别为50,70,100,130kHz的汉宁窗调制正弦波信号进行检测,结果分别如图7、图8、图6和图9所示。
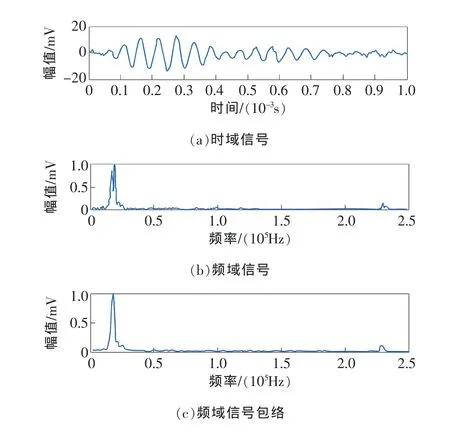
图7 激励频率为50kHz时检测结果
2.3 不同波数的试验
不同波数的选取对检测结果的影响很大,对于低于200kHz的Lamb波,每个周期模态的时间相对较长,因而不易选取周期数较多的信号,否则较容易与回波信号叠加在一起不利于分析。针对激励频率100kHz的汉宁窗调制正弦信号,在波数分别为3,5,7条件下进行试验,实验结果分别如图10、图6和图11所示。
3 结果分析
具体在选择波形时一方面要遵循在中心频率处能量越集中以及频带越窄越好的原则,另一方面由于超声波干耦合检测没有耦合介质,要求接收的信号具有高能量E。对于信号质量可引入品质因数Q作为衡量参数,其定义为
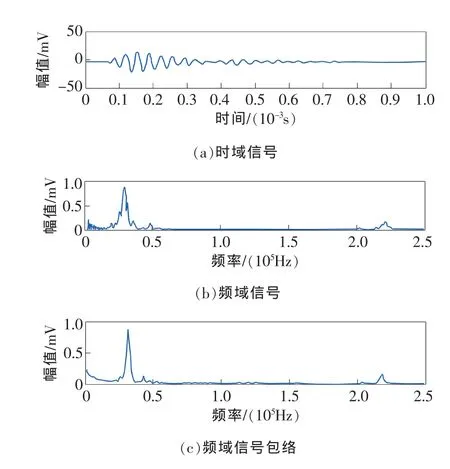
图8 激励频率为70kHz时检测结果
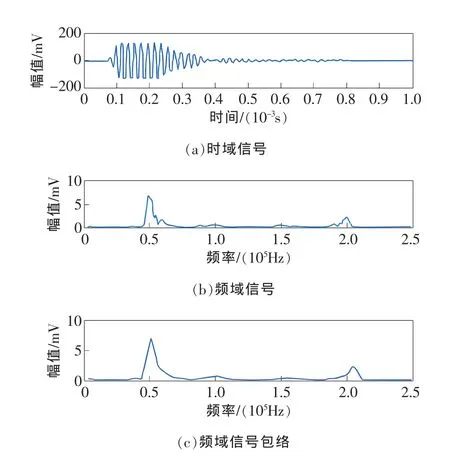
图9 激励频率为130kHz时检测结果
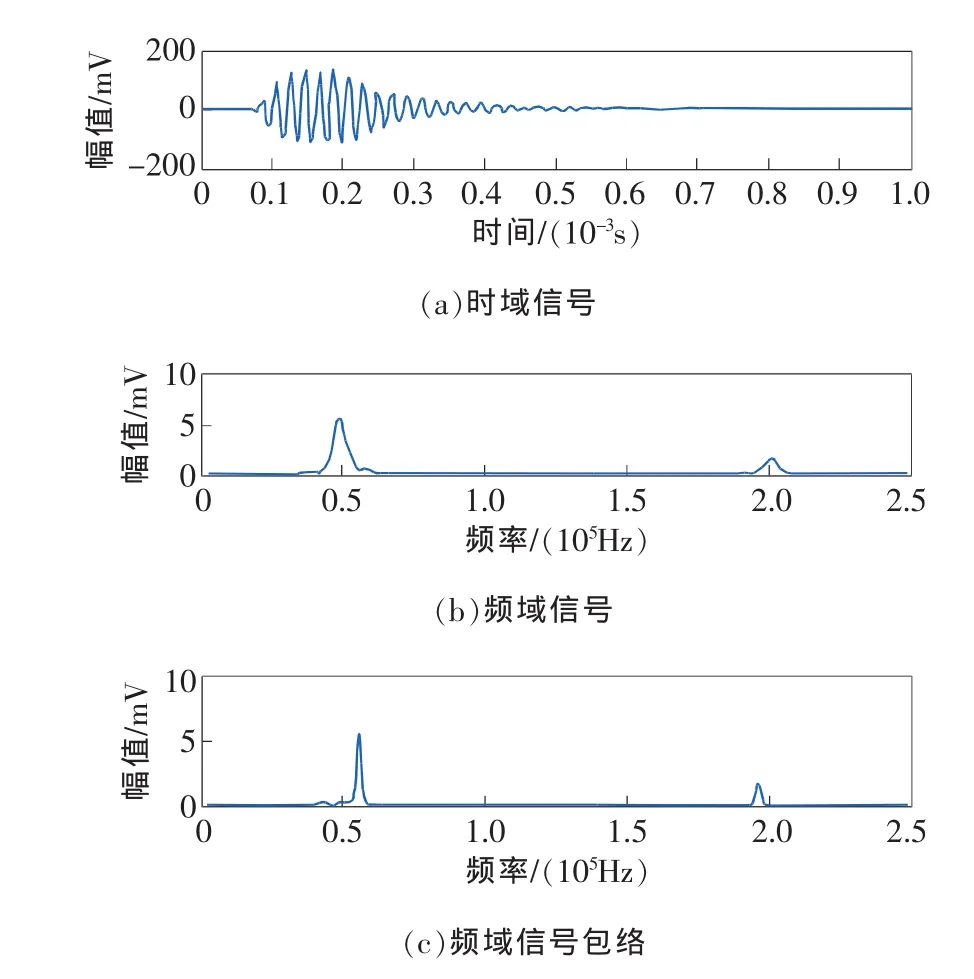
图10 激励波形波数为3时检测结果

图11 激励波形波数为7时检测结果

式中:f0——中心频率;
df——频率带宽。
一方面,Q值越大,表明信号质量越好,能量越集中,带宽越小;反之,信号能量越分散,带宽越大,信号质量越差。
1)在试验的5种波形中,当激励信号为锯齿波时,探头可以工作,但无法接收到有用的检测信号,因此锯齿波不宜作为激励波形。根据另外4种频域信号包络计算的Q值及E值如表1所示,柱状图如图12所示。

表1 不同激励波形时的Q值和E值
从图12中可以看出,4种激励波形均能使探头正常工作,接收探头均能采集得到含有缺陷信息的检测信号,其中采用方波激励时Q值和E值都较小;高斯窗调制正弦波激励时E值较大,但Q值较小都不适合作为干耦合探头的激励信号;海明窗和汉宁窗调制的正弦信号Q值和E值都较高,尤其是汉宁窗调制信号,更适合作为激励信号。
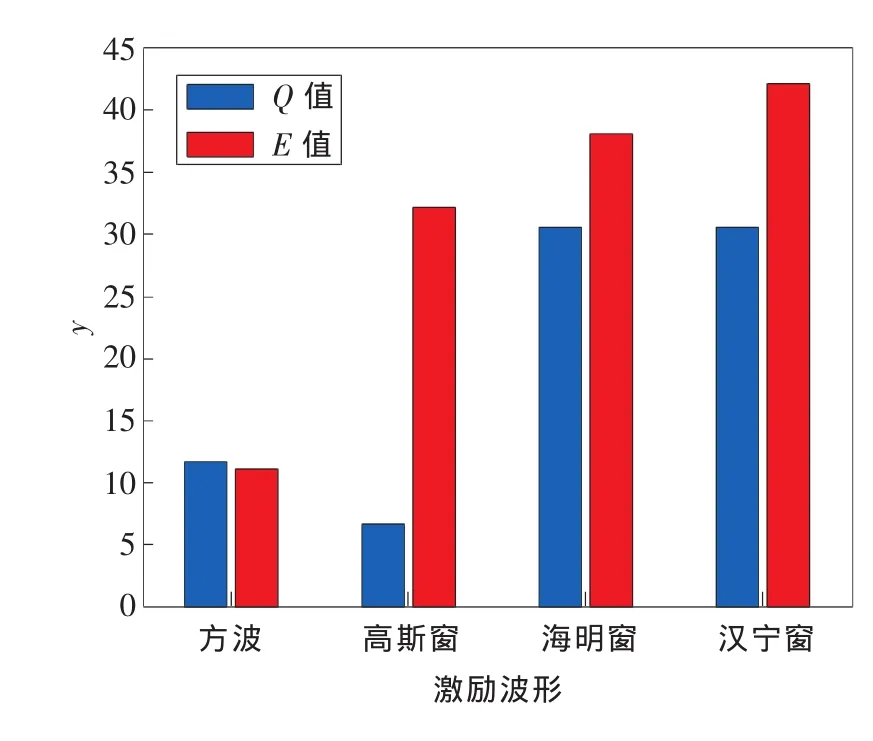
图12 不同激励波形时的Q值和E值柱状图
2)根据不同激励频率条件下的检测结果,计算出50,70,100,130kHz时的Q值和E值,如表2所示,其柱状图如图13所示。由图可知,随着激励频率的增大,接收信号的E值逐渐增大,而Q值先增大后减小,当频率为100kHz时达到最大,因此综合Q值和E值,选择汉宁窗调制正弦波信号的激励频率为100kHz。

表2 不同激励频率时的Q值和E值

表3 不同激励波数时的Q值和E值
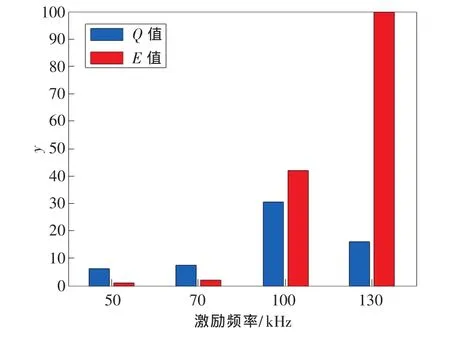
图13 不同激励频率时的Q值和E值柱状图
3)波数分别为3,5,7时,计算出的Q值及E值如表3所示,根据检测信号包络绘出的柱状图如图14所示。从图中可以看出,随着激励波波数的逐渐增大,Q值基本保持不变,波数为5时稍大;而E值逐渐减小,波数为7时,降低幅度较大,波数为3和5时,E值比较接近,因此选择激励信号波数为5。
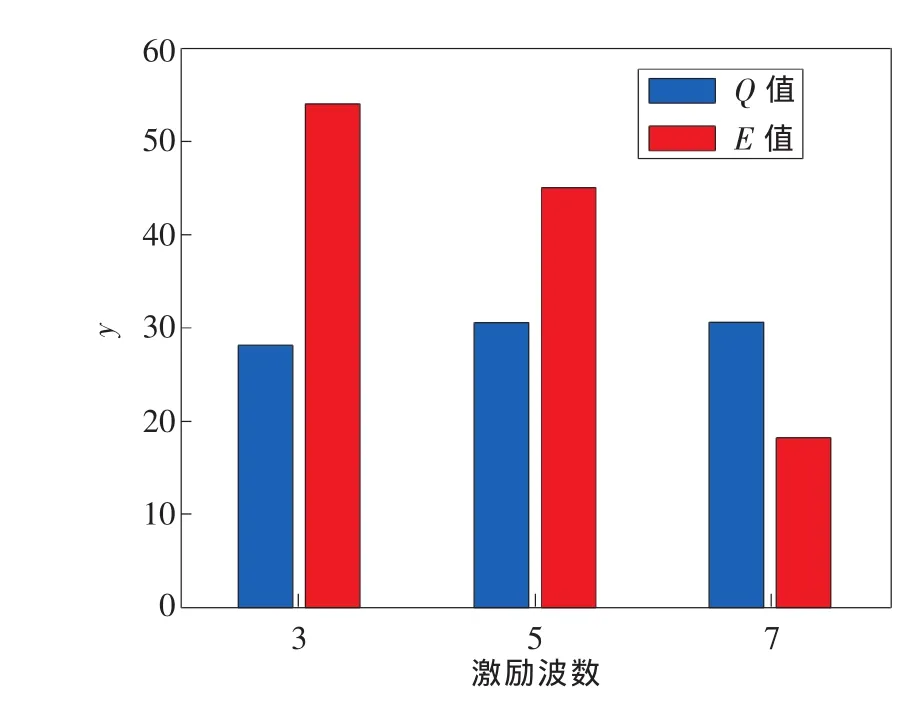
图14 不同激励波数时的Q值和E值柱状图
4 结束语
1)干耦合超声检测过程中,脱粘和未脱粘区域能量泄露存在区别,可以根据接收检测信号的能量来判断缺陷的存在与否。
2)不同激励信号作用于干耦合超声波探头,导致检测信号的中心频率、带宽、能量集中性等都有所不同,引入的品质因数Q值和能量E值可作为选择最优激励信号的依据。
3)针对不同的检测对象,选用的激励波形、波数、频率等参数都有所不同,对于玻璃纤维/丁腈橡胶两层粘接板,宜选用5周期汉宁窗调制正弦波作为干耦合超声检测的激励波形。
4)由于结构中超声Lamb波传播过程比较复杂,影响接收信号能量、带宽等特征参数的因素很多,比如边界、试件中界面的波形转换等,下一步需对这些问题进行更深入的分析。
[1]郑海平,武金宇,阮宏斌,等.非金属复合材料超声干耦合自动探伤方法研究[C]∥陕西省第十届无损检测年会论文集,2006:25-30.
[2]穆洪彬,吴朝军,吴晨,等.干耦合超声检测技术在某火箭发动机喷管在役检测中的应用[J].无损检测,2013,35(6):40-43.
[3]周正干,马保全,孙志明,等.空气耦合超声检测中脉冲压缩方法的参数选优[J].北京航空航天大学学报,2015,41(1):1-7.
[4]魏东,周正干.该进的非线性调频脉冲压缩方法在空气耦合超声检测中的应用[J].机械工程学报,2012,48(16):8-13.
[5]KOMSKY I N.Transducer modules for dry-coupled ultrasonic inspection of aircraft structures[J].Review of Quantitative Non-destructive Evaluation,2004(23):713-720.
[6]KOMSKY I N.Modular dry-coupled ultrasonic probes for field insepections of multi-layered aircraft structures[M]. Health Monitoring and Smart Nondestructive Evaluation of Structural and Biological Systems IV,2005.
[7]DUWATTEZ J,AUGEREAU F.Dry coupling ultrasonic high frequency sensors for detection of surface and tribological properties at a sub-micrometric scale[J].Journal of Nondestructive Evaluation,2003(22):79-92.
[8]ROBINSON A M,DRINKWATER B W,ALLIN J.Dry coupled low-frequency ultrasonic wheel probes:application to adhesive bond inspection[J].NDT&International,2003(36):27-36.
[9]DIXON E C,PALMER S B.Improvements to dry coupled ultrasound for wall thickness and weld inspection[J]. Review of Progress in Quantitative Nondestructive Evaluation,2000(12):1779-1786.
[10]SOLODOV I,DORING D,BUSSE G.Aircoupled Lamb and Rayleigh waves for remote NDE of defects and material elastic properties[J].The 10th International Conference of the Slovenian Society for Non-Destructive Testing,2009(30):37-45.
[11]川嶋紘一郎.ものづくりのための超音波非破坏评价·检査[M].东京:养贤堂,2009.
[12]常俊杰,卢超,川嶋紘一郎.非接触空气耦合超声波的材料无损评价与检测[J].浙江理工大学学报,2015,33(4):532-536.
[13]李远,秦自楷,周志刚.压电与铁电材料的测量[M].北京:科学出版社,1984:15-27.
[14]王召巴,金永.复合材料多界面脱粘超声检测技术[J].太原师范学院学报,2003(1):45-47.
[15]魏勤,骆英,王自平,等.Lamb波驱动器的最佳激励波形选择[J].压电与声光,2011,33(6):863-866.
(编辑:李刚)
Research on dry coupled ultrasonic excitation signal
AI Chun’an,CAI Xiaofeng,LI Jian,LIU Kaixuan
(Rocket Force University of Engineering,Xi’an 710025,China)
To ensure the operation of dry coupled ultrasonic probe,theoretical analysis and experiment are jointly applied to select its excitation signal.The projectile energy of the dry coupled ultrasonic probe is low because it has direct contact with the specimen.The energy(E)of the receipt signal differs greatly under different bonding conditions.Quality factor(Q) can represent the bandwidth and intensity distribution of receipt signal and they can be used as the basis for selecting excitation signal.According to the expression formula of each signal,sinusoidal impulse signal modulated by square wave,sawtooth wave,Gauss window,Hamming window and Hanning window were used for test.Test results show that the optimal excitation waveform for the glass fiber/nitrile rubber bonded composite plate is the sine pulse signal with an excitation frequency of about 100 kHz modulated by 5-cycle Hanning window under constant repetition frequency and voltage amplitude.It provides a basis for the detection of dry coupled ultrasonic probe.
dry coupled;ultrasonic wave excitation;window function;quality factor
A
:1674-5124(2016)12-0012-06
10.11857/j.issn.1674-5124.2016.12.003
2016-03-23;
:2016-04-28
国家自然科学基金项目(51275517)
艾春安(1964-),男,湖南邵阳市人,教授,博士生导师,研究方向为固体火箭发动机无损检测。
