基于共生理论的供应链上下游企业库存水平策略研究
2016-02-06曾新韵谭远顺
杨 金,曾新韵,谭远顺
(重庆交通大学 数学与统计学院,重庆 400074)
基于共生理论的供应链上下游企业库存水平策略研究
杨 金,曾新韵,谭远顺
(重庆交通大学 数学与统计学院,重庆 400074)
运用共生理论,在下游企业库存水平相对增长率为线性反应函数的基础上,提出了Holling II非线性功能性反应函数关系的数学模型,得出供应链上下游企业库存水平稳定的充分条件,当这一稳定的平衡状态被破坏时,其外围出现一系列关联紧密的稳定平衡态,供应链中的上游企业和下游企业仍达到一种动态的平衡.这种现象符合经济学中的杠杠原理,使得此模型更加合理,相关结论有助于上游企业和下游企业作出更加合理的库存决策.
Holling II功能性反应函数;供应链;平衡态;极限环;库存
随着互联网、ERP、电子商务等信息技术在企业中的广泛应用,如何有效管理库存,使它既可以维持一个较高的服务水平,又可以减少不必要的库存成本费用.许多学者对供应链上下游企业的库存水平进行研究,胡建波等[1]研究了供应链库存管理策略;Zhang等[2]通过考虑多个敏感需求流的库存系统,分析牛鞭效应所产生的后果;Fu等[3]研究两级供应链中供应商和分销商在供应方面的合作库存决策,说明供应方面的协作能够提高供应链性能的稳定作用和服务水平.随着对供应链库存问题的深入研究,学者们建立模型,运用算法,对供应链库存进行分析,倪冬梅等[4]建立需求预测与库存决策集成模型,验证其求解方法有效性,表明集成模型在减少缺货和节约成本方面具有优势;柳键等[5]基于需求和供应都不确定,建立定期检查补货模式下的供需双方库存模型,研究供应链库存协调与优化;何继善院士等将上下游企业管理策略和生态数学模型联系起来,在下游企业库存水平相对增长率为线性反应函数的基础上,研究了集群中上下游企业库存的稳定性[6];此后一系列文献以数学和生态学的原理与工具对管理现象进行了卓有成效的探究,得出了很好的结论.王子龙等[7]研究了企业集群共生演化模型,韩二东等[8]研究了生态学视角下港口产业集群共生模型的稳定性等.以上这些文章更多的是对供应链上下游企业库存策略的定性说明,对于模型的定量分析也只侧重于当系统存在平衡态时的上下游企业之间库存水平稳定性的描述,而当供应链上下游企业库存状态不稳定时,会发生何种现象,则没有研究说明.因此,本文运用共生理论,改进下游企业库存水平相对增长率为线性率的情形,提出了下游企业库存水平相对增长率为Holling II函数关系的数学模型,推广了相关结论,得到一定条件下供应链中的上游企业和下游企业达到一种动态平衡的充分条件,使得模型更加合理,符合经济学中的杠杠原理,相关结论有助于上游企业和下游企业作出更加合理的库存决策.
1 模型建立
考虑由一个上游企业和一个下游企业构成供应链.
对于上游企业,若没有下游企业来购买它的产品,其库存水平x1呈logistic增长[6]:
(1)
其中,xi表示供应链上游企业的库存水平,r表示上游企业库存水平的自然增长率,t表示时间,K表示在一段时间区域内,以及有限的资源约束的条件下,上游企业的极限库存水平.
对于下游企业,若没有上游企业给它提供产品,其库存水平按几何级数减少[6]:
(2)
其中,x2表示供应链下游企业的库存水平,d表示下游企业库存的消耗率.
若供应链中的下游企业购买上游企业的产品.此时,供应链上下游企业库存水平的关系满足Lorka-Volterra方程.因此,供应链上下游企业库存的共生模型[6]为:
(3)
其中,α表示下游企业对上游企业产品的购买率,e表示下游企业将上游企业的库存产品转化为自身产品的效率.该模型简单描述了供应链中上游企业和下游企业的供求关系.
模型(3)假设两个企业库存量的相对增长率是线性函数[9],这一个假设使得模型十分的简单,虽然能将模型中的几个参数和这两个企业的相互作用关系对应起来,认为上游企业库存水平与库存量成正比,供应链上游企业库存水平越高,下游企业在单位时间内购买的产品也就越多,这在一定程度上是合理的,但是下游企业不可能购买无穷多的产品,忽略了下游企业库存产品的消化饱和因素.为了更好地反映实际情况,应该假定功能性反应与供应链上游企业库存水平的关系是一种包含着饱和因素的函数关系.因此,我们引进Holling II功能性函数[10~12].
(4)
其中,ω>0为常数.该函数描述了上下游企业之间库存量之间的相互影响.上游企业产品越多,在开始阶段对下游企业的影响越大,但是,随着时间的推移,下游企业对产品的需求程度降低,在一定时刻达到饱和值,此时,上游企业的产品对下游企业的影响将稳定于某一恒定值,其关系可以由式(4)很好地加以描述.
将式(4)带入模型(3)中,得到具有II类功能性反应的供应链上下游企业库存水平共生模型:
(5)
模型中假定各个参数都是与时间无关的常数,而且在企业的运作中,库存水平没有受到突然政策或者不可抗拒灾难的影响.
2 模型分析
2.1 稳定性分析
对模型(5)进行无量纲化,令
dt=(1+ωx1)dτ,
为方便模型计算分析,令
则模型(5)化为
(6)
其中,a1=a,a2=ωa-b,a3=-bω,β=eα-dω.易知,若模型存在非平凡平衡位置,则必有β≠0.为了简单起见,我们作变换:
则模型(6)化为(新的变量仍记为x1,x2,t)
(7)
其中,
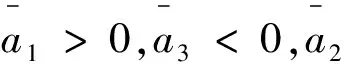
求出平衡态和雅可比矩阵
将A带入特征方程
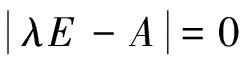
中,得到对应的特征值,见表1.

表1 模型(7)的平衡点以及对应的特征值
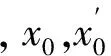
记
取合适的r使得Φ(x1,r)为定号,也就是说,取r使得Φ(x1,r)=0.关于x1无实根,只要r满足不等式,因而当r1rr2时,f1(r)0.所以当0时,只要r满足r1 带入其中,正平衡点为 说明无论供应链中的上游企业和下游企业是处于何种库存水平,要想供应链继续维持,以及双方都获得极高的收益和较低的库存成本,上游企业和下游企业的库存水平处于这个稳定的平衡位置是供应链上下游企业最好的选择.因此,供应链上游企业和下游根据实际情况建立数学模型,分析其稳定性,可以让供应链上下游企业稳定地发展下去,并获取更高的利益,达到分析建立供应链上下游企业库存模型的目的,模型达到稳定的条件为 2.2 极限环现象分析 2.2.1 极限环存在性 首先研究供应链上下游企业的极限环现象是否存在.极限环存在性的判定方法主要有两类:第一类是根据环域定理或由它所推演出来的判定定理;第二类是基于分支理论.本文运用第一类方法研究供应链上下游企业的极限环现象. 图1 AOR1B构成的Bendixson区域图 所以,直线x=x0是无切的.模型(7)的轨线在其上的穿过方向如图1所示.再考虑直线L2=x2+x1-K=0,这里K>0充分大.于是关于模型(7)有 因为只考虑直线L2=0在区域0x1x0内的一部分线段AB,显然当K取得充分大时上式右端在区间0x1x0内恒为负,实际上只要取 极限环实际上就是一条孤立的闭轨线.当极限环存在时,说明从任何一点初始值出发,时间经过无穷大,不会收敛到一个平衡位置,而是会趋近于一段闭合的轨迹.如线性规划中求出的最优解,不是一个孤立的解,而是一个区域. 2.2.2 极限环唯一性 在研究极限环存在的前提下,我们研究这极限环是否唯一.对模型(7)作变换 其中 则模型(7)变化为 (8) (9) 其中, 因为当u≠0时, ug(u)=uz(eu-1)>0; 成立. 极限环除了在研究轨线的定性结构中扮演着重要角色外,还有着重要的实际意义,反映了现实世界中大量存在的周期震荡现象.在实际情况中,上游企业和下游企业的库存水平不是稳定在一个数值(平衡位置)上的,它们会出现周期性的变化.也就是说,虽然平衡位置是不稳定的,但是其周围会存在一个稳定的极限环.如果这个极限环是唯一的,则上游企业和下游企业的库存水平是稳定在一个周期性的轨道上.在供应链上下游企业实际运作过程中,上游企业和下游企业相互协调,当上游企业的库存水平较低,而下游企业产出水平较高;上游企业的库存水平较高,而下游企业的库存水平较低时,在这个协调的过程中,都可以让这个供应链继续维持下去,使得库存系统状态的不确定和动态复杂性降低,同时使得供应链上下游企业获取高收益. 对供应链上下游企业的库存水平进行模型分析,其初衷是为了供应链中的企业能够适应外部环境(经济全球变化、顾客需求变化、竞争态势变化)、内部环境(组织和管理观念)和科学技术的快速变化.稳定的供应链是构成供应链的节点企业相对稳定,也就是建立在供需关系上的节点企业的关系相对稳定.供应链上下游企业的库存关系是一个动态的系统,企业库存受到供应链成员的信任程度、运作能力、资源的互补性、风险程度和信息分享程度的影响.若库存管理不当,将导致库存的不足或者过剩.库存不足将错过送货、失去销售额、使客户不满、产生生产力瓶颈等;而库存过多则要占用更多的资源.而分析供应链上下游企业的稳定性,就是在企业适应内外部环境和科技快速变化的基础上,指导企业作出合理的库存决策,使得供应链上下游企业获得更大的利益. 本文提出了第二类功能性反应函数,使得供应链上下游企业之间库存的相互影响作用力具体的表现出来.根据实际探访某供应链上下游企业,通过数据分析,选择适当的参数数据,建立模型,通过求解,分析平衡态和极限环现象.我们根据实时的数据,分析此时的状态,有利于供应链中的上游企业和下游企业作出正确的决策和措施,具有实用价值. 供应链上下游企业的库存关系是一个动态的系统,其企业的共生关系是动态的关系,共生模型的各个数据随时都在发生变化,变化中出现了许多现象,我们建立模型,用量化的方式了解这些现象,分析稳定点是否稳定、是否出现了极限环现象、这些极限环又是否稳定和唯一.因为供应链上下游企业都是独立的实体,是平等的关系,彼此之间是在共同利益下的优势互补,拥有独立的决策权,两者通过共同的目标得到很好的统一.除了判断该平衡点是否稳定和不稳定时的极限环现象,我们还可以研究其它问题,如该平衡点稳定,是渐进稳定还是全局稳定,系统稳定的前提下,从靠近稳定点开始运动,当时间趋近于无穷大时,运动收敛到稳定点,就说明这个系统是渐进稳定的,全局稳定则说明从任意一点出发,时间趋近于无穷大时,运动都会收敛到该稳定点. 本文中企业的库存水平是随着时间变化的函数,其参数都是与时间无关的常数,企业的库存水平只与瞬时库存水平有关,不考虑滞后效应.在企业的运作中,库存水平没有受到突发政策或者不可抗拒灾难的影响.但是,在实际的供应链上下游企业运作过程中,其参数都是随着时间的变化而变化,并不是一成不变的.进一步地,我们可以分析研究非自治模型和时滞模型,考虑随时间变化的函数和滞后效应,以及建立脉冲微分系统,考虑瞬时突变现象对供应链上下游企业的影响,充分、深刻及精确地反映事物的变化规律. [1] 胡建波,陈敏.供应链库存管理策略[J].企业管理,2013(4):66-68. [2] ZHANG Xiaolong,Gerard J Burke.Analysis of compound bullwhip effect causes[J].European Journal of Operational Research,2011,210,514-526. [3] FU Yonghui,Rajesh Piplani.Supply-side collaboration and its value in supply chains[J].European Journal of Operational Research,2004,152,281-288. [4] 倪冬梅,赵秋红,李海滨.需求预测综合模型及其与库存决策的集成研究[J].管理科学学报,2013,16(9):44-52. [5] 柳键,马士华.供应链库存协调与优化模型研究[J].管理科学学报,2004,7(4):1-8. [6] 何继善,戴卫明.产业集群的生态学模型及生态平衡分析[J].北京师范大学学报:社会科学版,2005(1):126-132. [7] 王子龙,谭清美,许箫迪.企业集群共生演化模型及实证研究[J].中国管理科学,2006,l4(2):141-148. [8] 韩二东,郭鹏.生态学视角下港口产业集群共生模型的稳定性[J].华中师范大学学报:自然科学版,2013,47(6):819-823. [9] 肖燕妮,周义仓,唐三一.生物数学原理[M].西安:西安交通大学出版社,2012. [10] Holling C S.The functional response of predators to prey density and its role in mimicry and population regulation[J].Mem Ent Canada,1965,45:3-60. [11] 陈兰荪.数学生态学模型与研究方法[M].北京:科学出版社,1991. [12] 陈兰荪,陈键.非线性生物动力系统[M].北京:科学出版社,1993. [13] 马知恩,周义仓.常微分方程定性与稳定性方法[M].北京:科学出版社,2012. [14] Hoberg K,Bradley J R,Thonemann U W.Analyzing the effect of the inventory policy on order and inventory variability with linear control theory[J].European Journal of Operational Research,2007,176,1620-1642. [15] 王晶,王寻.受约束供应链模型的复杂动力学行为[J].系统工程理论与实践,2012,32(4):746-751. (责任编辑:张冬冬) Research on the inventory level strategy of upstream and downstream firms in supply chain based on symbiotic theory YANG Jin,ZENG Xinyun,TAN Yuanshun (SchoolofMatnematicsandStatistics,ChongqingJiaotongUniversity,Chongqing400074,China) This paper proposes a mathematical model in which the relative growth rate of downstream firms’ inventory level satisfies the Holling II functional response function based on symbiotic theory,which expands the linear case.The results indicate that when,the upstream and downstream firms’ inventory level is stable,the original stability of the equilibrium is broken,and a series of close-related new equilibria are generated.The model appears many dynamical equilibria.This phenomenon accords with the lever principle in economics,which makes the model more reasonable.These related conclusions are helpful for upstream and downstream firms to make more reasonable decisions in their managements. Holling II functional response function;supply chain;equilibrium;limit circle;inventory 2016-08-15 重庆市研究生教学改革研究项目(yjg2014162);重庆高校创新团队建设计划资助项目(CXTDX201601022). 杨金(1986-),男,安徽合肥人,重庆交通大学数学与统计学院讲师,博士研究生.研究方向:生物数学. C939 A 1008-2441(2016)06-0012-07
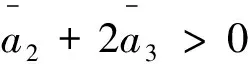
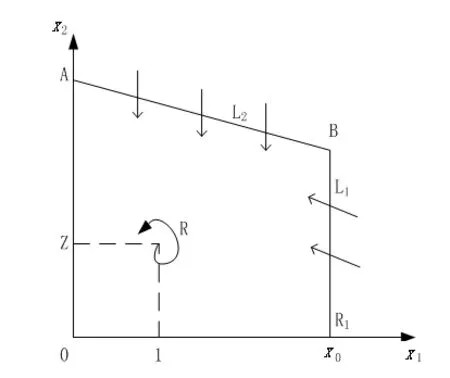
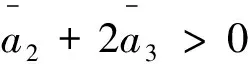
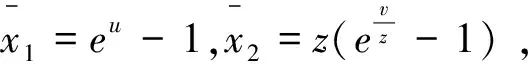
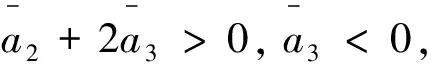
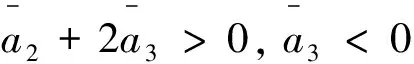
3 结论
