量子密码对比现代密码的优势
2016-02-06钟方天
◆钟方天 朱 浩
(东北师范大学 吉林 130117)
量子密码对比现代密码的优势
◆钟方天 朱 浩
(东北师范大学 吉林 130117)
在近十年来,随着信息时代的到来和网络的日渐发达,人们对于信息的安全性要求越来越高。量子计算研究飞速发展,现代密码学的地位正遭受着前所未有的挑战。本文简要介绍了传统密码和量子密码的基本概念,通过密码技术对比,强调量子密码比传统密码更加安全。
信息安全;现代密码;量子密码;密码技术
0 引言
现代密码学是建立在传统密码学的基础之上,基于精确的安全假设,使用更安全证明的方法以及更精确陈述的证明方案而来的。量子密码学的思想的萌芽的出现是在20世纪60年代末,由美国Thomas J.Waston研究中心的Charles H.Bennett与加拿大Université de Montréal的Gilles Brassard在1982年美洲密码学会上联合发表的第一篇论文中提出,第一台原型样机则出现在1989年。
1 现代密码学和量子密码学
1.1 现代密码学概念
现代密码学是在传统密码学的基础上发展起来的。通常由五部分组成,分别为明文(M)、密文(C)、加密函数(E)、解密函数(D)、密钥(K)。它主要基于如大数的分解和离散对数问题等应用逻辑数学难题。
在现代密码学中应用最为广泛和体制最为完善的就是对称密码和公钥密码。
1.2 量子密码学概念
人们目前主要通过光钎来进行大量数据稳定且快速传输的,但也有在探寻另一种方式——就是直接以光束来传送数据。怎样才能保证数据传输的安全性呢?这就是人们目前正在研究的——量子密码学(Quantum Cryptography)。量子物理学的研究表明,每个光子都由特定的线偏正和圆偏正两个特性组成。量子密码学利用这一特性,就可达到安全的进行随机密钥分配。
2 量子密码学对比现代密码学
2.1 现代密码学对称密码的缺陷
对称密码算法有两种基本类型:分组密码和序列密码。分组密码是在明文分组和密文分组上进行运算。主要有五种操作模式:电子密码本(ECB)、密码分组链接模式(CBC)、输出反馈(OFB)、密码反馈模式(CFB)、计数器(CRT)模式。
电子密码本(Electronic Code Book,ECB)模式是将一个明文分组加密成一个密文分组。ECB所带来的问题是:由于现代密码加密解密的通讯方式的缺陷,敌人可以监听并获取到密文,且不被发现。另外一个更为严重的问题是敌人可以在不知道密钥的情况下随意修改被加密过的消息,这样就可以欺骗指定的接受者。假设银行采用这种模式有如下一组分组情况:
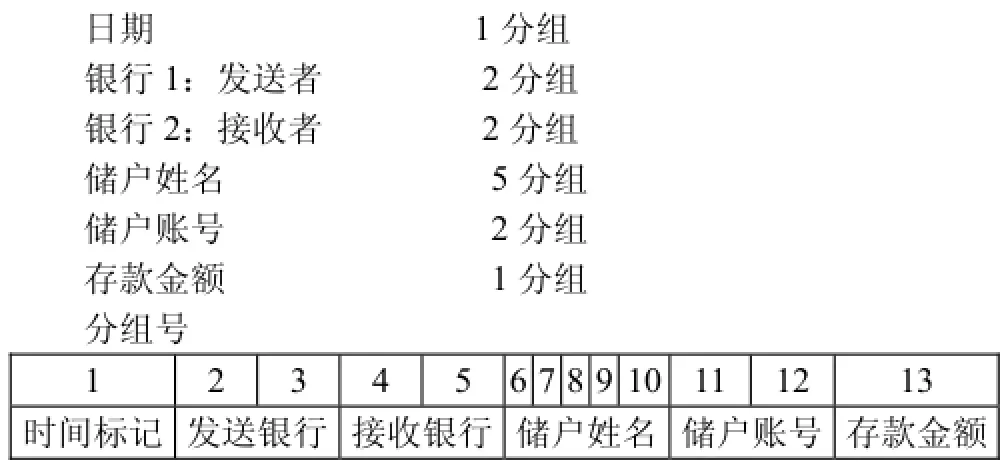
假设A是窃听者,用这种系统他可以很容易的根据多条密文分析出消息所具有的共性,现在他就可以利用这个共性来实现资金往自己的账户转账了,只需简单地将姓名和账号换上他自己的,然后查看自己的进账就行了。
分组链接模式(Cipher Block Chaining,CBC)是将上一个分组的加密结果反馈到当前的加密中。CBC潜在的问题:因为前一个分组加密的分组都将反馈到下一个分组,所以A可以通过改变一个密文分组,控制其余解密的明文分组,也可以在加密信息的后面加上一些分组却不被察觉。
输出反馈模式(Output-Feedback,OFB)模式是通过将明文分组和密码算法的输出进行异或来产生密文分组。OFB存在的问题是明文很容易被控制窜改,任何对密文的改变都会直接影响明文。
计数器模式(Counter mode)是使用序列号作为当前算法的输入,每一个分组完成加密后,计数器都要增加一个常数。计数器存在的问题跟输出反馈模式相同。
2.2 量子密码的特性优势
量子密码是基于量子的物理特性为基础的,具有量子的不可克隆以及测不准定理的特性。量子不可克隆定理的证明如下。
我们假设存在一个能够完全克隆任意量子比特的系统。
存在两个任意的|Ø)和|ψ)量子状态,因此我们所要完成的就是将它克隆到另一个与他们不同的量子状态|k)上。我们用一个运算符U来描述这个运算。那么这个拷贝算符就要满足以下性质:

这个等式只有两个解是(Ø|ψ)=0和(Ø|ψ)= 1.这意味着,要么Ø = ψ,要么Ø与ψ正交。只能克隆相同或正交的状态,这与我们当初假设可以任意克隆各种状态相矛盾,不可克隆原理证明完毕。量子不可克隆定理即不存在任何物理系统可以精确的复制未知的量子态。利用此特性量,子密码上也就不可监听,因此就可以利用这一特性进行信息的保密传输,由此可见,量子密码进行通讯是安全的。
测不准原理,对于任意的A,B两个观察量,用Dirac记号,测不准关系可表示如下<(ΔA)2><(ΔB)2>≥(||<[A,B]>||2)/4,其中ΔA = A -<A>,ΔB = B -<B>,[A,B]=AB - BA。
<(ΔA)2>与<(ΔB)2>是A,B不确定性的量度。对不可对易的可观察量A,B[A,B] ≠ 0,如果<(ΔA)2>减少,<(ΔB)2>就会增加,反之亦然。在量子世界中存在这种基本的不确定性,利用这种不确定性就可以用来产生秘密密钥。
量子态的测不准原理表明对于任意一个物理量的测量都必对另一物理量产生干扰,这一性质使得双方无须事先交换密钥就能进行绝密通信成为可能。例如银行1和银行2在一次通信中采用量子密钥分发协议进行通讯,假设有窃听者,使用量子测量仪测量线偏正,由于对光子实际偏振态一无所知,只能随机选择。如果选择正确,光子将穿过他的偏振仪,反之他选择的偏振仪的偏振态错误,必将影响该光子的偏振态,导致银行2测量结果和银行1发射的光子的偏振态不同。这样银行1和银行2通过对该密钥序列的序列码进行校验,就会发现他们所建立的密钥序列不一样,从而知道有人在窃听,他们丢弃这个密钥即可。
2.3 现代密码学公钥密码的劣势
现代密码学公钥密码算法是1977年由 RON、Adi、Leonard一起提出的,立基于数论事实:计算两个大质数的乘积十分容易,但是对其乘积进行因式分解却异常困难,因此就可以将质数乘积公开作为加密密钥。现代密码学公钥密码破解主要基于大数的分解,要想破解这个系统就变成了计算复杂问题,目前对于公钥密码系统最好的攻击方式就是穷举攻击,假定密钥是由m位组成,采用计算机计算的复杂度就为2m/2次,然而随着分布式计算和量子计算机理论日趋成熟,计算速度加快,它将难逃此劫。
2.4 量子密码学密钥分配的优势
量子密钥分配基于量子物理学,它能够安全保证通讯双方通过一个量子通道发送私钥,私钥由量子态标记。接着我将介绍一个现有的量子密钥分配算法,基于伽罗瓦群论,并在此基础上证明它的复杂度大于现代密码学的公钥密码算法。当Iij= 1时,让单位圆(Iij)n╳n =满足I☉A = A,令Me= M☉M☉M…☉M,e∈Z+,代表矩阵M在矩阵M下的☉操作,以下讨论的问题都是在有限域的范围中进行的。
当n > 1时.那么左边的式子等于

右边的式子等于

因此左边和右边是相等的,满足交换律。
第二步:选择一个非0整数t1,t2,t3∈{0,1,……,ψ(p)}且t1 ≠ t2 ≠ t3,ψ(p)是p的欧拉函数。
这个公钥是由A,B,D,Y1,Y2,Y3 和一个素数组成,私钥是由t1,t2,t3组成。

3 结语
量子密码克服了现代密码固有的特点,且拥有安全性能高,信息传递效率高,传送容量大等特点,吸引了越来越多的国家参与到此方面的研究,目前我国应用于实践的项目有沪杭量子通信干线,陆家嘴量子通信金融网以及刚发射的第一颗量子卫星等,因此量子密码的发展前景极为广阔。
[1]蒋军,殷志祥.DNA密码对比传统密码学与量子密码学的优势与不足[J].科技视界,2012.
[2]柴小文,马维华.量子密码学安全协议的研究[J].微机发展,2002.
[3]WU WanQing,ZHANG HuanGuo,WANG HouZhe n,MAO ShaoWu,JIA JianWei,LIU JinHui.A public k-ey cryptosystem based on data complexity under quant-um envir onment[J].SCIENCE CHINA Information Scienc-es,2015.
[4]汤永龙.浅谈传统密码学和量子密码学原理[J].计算机光盘软件与应用,2011.
[5]曾贵华,王新梅.用量子效应实现身份认证[J].通信保密,2000.
[6]刘传才.量子密码学的研究进展[J].小型微型计算机系统,2003.
[7]Butter W T,et al.Free-space quantum-key distribution [D].Phys.Rev.A,1998.
[8]Wu W Q,Zhang H G,Wang H Z,et al.Polynomial ti me quantum algorithms for finding the linear structures of Bo olean function.Quantum Inf Process,2015.
[9]张福泰,孙银霞,张磊,耿曼曼,李素娟.无证书公钥密码体制研究[J].Journal of Software,2011.
[10]Usenko,Vladyslav C,Filip,Radim,Trusted Noise in Con tinuous-Variable Quantum Key Distribution:A Thre-at and a Defense[J].MDPI AG,POSTFACH,CH-4005 BA-SEL,SWIT ZERLAND,JAN 2016.
[11]黄靖正.量子密钥分配系统实际安全性研究[D].中国科学技术大学,2014.
[12]李佳.量子密码体系研究[J].科技广场,2013.
[13]Yang,Fan;Yang,Guowu;Hao,Yujie,The Model- in g Library of Eavesdropping Methods in Quantum Cry-ptogra phy Protocols by Model Checking[J].International Journal of Theoretical Physics,2016.
[14]Molotkov,SN,On the complexity of search for ke-ys in quantum cryptography.JETP LETTERS[J].2016.
[15]Mowa.NI;Doh;Chae.K;Securing information Flow in Content Deliver Networks with Visual and Quantum Cryptog raphy.
[16]Chen.Chi-Yuan;Zeng,Guo-JYun;Lin,Fang-Jhu;Qua-n tum Cryptography and its Application over the Internet-[J].IE EE NETWORK,2015.
[17]任伟.密码学与现代密码学研究[J].信息网络安全,2011.
[18]于红梅.数论密码学历史分析与未来发展展望[D].山东大学,2008.
[19]郭海明,白永祥.数论在密码学中的应用[J].电脑知识与技术,2010.
[20]吕兴凤,姜誉.计算机密码学中的加密技术研究进展[J].信息网络安全,2009.
