对K-means聚类算法欧氏距离加权系数的研究

◆郭 靖

（中国人民公安大学信息工程与网络安全学院 北京 100038）

对K-means聚类算法欧氏距离加权系数的研究

◆郭 靖

（中国人民公安大学信息工程与网络安全学院 北京 100038）

K-means聚类算法广泛应用于模式识别、图像处理和数据挖掘等领域中，有着简洁高效等优点。然而，传统的K-means聚类算法在以欧氏距离为度量函数时简单地把数据的各个属性平等对待，忽略了不同属性的重要性不同。本文结合统计学中描述数据离散程度的四种指标提出四种计算加权系数的方法，并通过实验比较这四种加权系数对聚类结果准确度的影响，以此来说明对欧氏距离加权的必要性和计算加权系数的简单可行的方法。

K-means聚类算法；欧氏距离；加权系数

0 引言

K-means聚类算法[1]是最著名的划分聚类算法之一，简洁、高效以及适应性强等优点使得它成为所有聚类算法中最广泛使用的。它的中心思想是：在数据集中随机选择K个对象作为初始聚类中心并代表K个类别；然后将其余的数据点依据它们到各初始聚类中心的欧氏距离划分到与其距离最近的类别中，以形成初始分类；最后对初始分类进行多次迭代修正，直到分类比较合理为止。传统的K-means算法认为数据的各个属性对聚类结果的贡献相同，没有考虑不同属性对聚类结果可能造成的不同影响，进而可能使聚类结果无法准确地反映数据类别的真实情况。

大量的相关研究表明：对K-means聚类算法中的欧氏距离引入加权系数可以提高聚类准确度。已知的加权方法包括：基于密度加权[2]，特征权值学习[3]，自适应加权[4]等。在2002年，Fabrizio[5]对已有加权系数的计算方法作了总结，分析了包括Document frequency，Information gain，Mutual information，Chi-square等多种加权系数计算方法的特性及适用领域。相关理论分析和实验结果指出每种计算方法在运算速度和聚类结果的精度等方面各有优劣。

本文从要聚类分析的数据本身入手，以数据各个特征的离散程度来确定加权系数的大小。对于任意两个属性特征c1、c2，如果c1样本的离散程度比c2的大，则可以认为c1属性在聚类中应占有更重要的地位。通过对c1属性赋予较大权值来调整特征空间，可以更准确反映类内相似度并得到更佳的聚类结果[6]。这种方法不需要分析人员额外输入其他的参数，保证了聚类结果的客观性，减少了工作难度，简单快捷，易于实现。

1 相关工作

1.1 K-means聚类算法

K-means聚类算法的主要思想是：首先，在需要分类的数据中随机寻找K个数据作为初始聚类中心；然后，计算其他数据距离这K个聚类中心的欧式距离，将数据归入与其欧式距离最近的那一类别，再对这K个聚类中的数据分别计算算术平均值，作为各个聚类的新的聚类中心；最后，重复以上步骤，直到完成想要的迭代次数或者新的聚类中心与上一次的聚类中心相同时结束算法。

K-means聚类算法步骤可以简单地描述如下：

输入：数据集U，假设包含n个数据对象，每个数据对象包含c维属性，要划分的类别的数目是k。

输出：聚类结果。

①从数据集U中随机选取k个数据对象，作为初始聚类的中心点。

②按欧氏距离公式（1）计算其余各数据对象到聚类中心的距离，然后将各个数据对象划分到离它们最近的那个中心点所属类中。

③重新计算各个类的中心。

④比较与上次聚类的划分是否有变化，如果没变化，则聚类过程结束，输出聚类结果；否则，返回步骤②继续迭代，直到聚类划分不再改变。

K-means聚类算法最常用的计算两个数据对象间的距离度量为欧氏距离，定义如下：

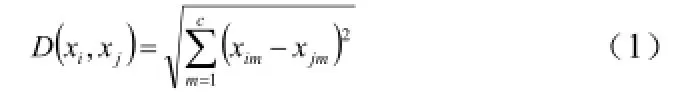
1.2 加权系数

在统计学中，描述数据离散程度常用的指标有：标准差（Standard Deviation），方差（variance），变异系数（Coefficient of Variation）。考虑到平均绝对偏差（Mean Absolute Difference）也能从某种程度上反应数据的波动情况，因此，本文通过这四个指标来确定加权系数。

定义数据集中每维属性的加权系数分别为1w，2w，...，cw（c为数据维度）。

标准差（standard deviation）就是方差的平方根：一组数据中的每一个数与这组数据的平均数的差的平方的和再除以数据的个数，取平方根即是。则加权系数为：

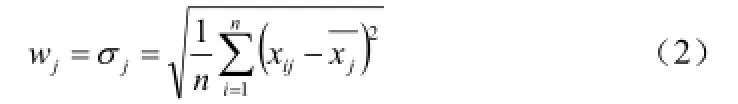
方差（variance）是各个数据与平均数之差的平方的和的平均数。则加权系数为：

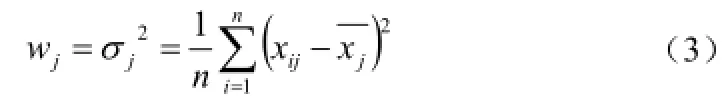
变异系数（Coefficient of Variation）是标准差与其平均数的比，当需要比较两组数据离散程度大小的时候，如果两组数据的测量尺度相差太大，或者数据量纲的不同，直接使用标准差来进行比较不合适，此时就应当消除测量尺度和量纲的影响，而变异系数可以做到这一点。则加权系数为：

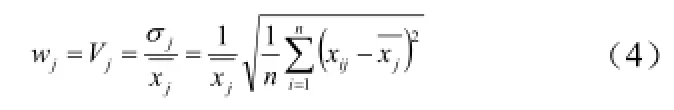
平均绝对偏差（Mean Absolute Difference）是所有单个数据与算术平均值的偏差的绝对值的平均。则加权系数为：

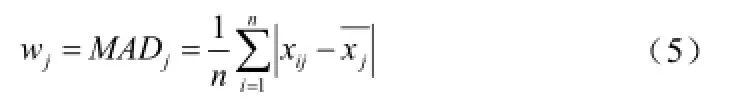
1.3 改进的K-means聚类算法

改进的K-means聚类算法步骤可以简单地描述如下：

输入：数据集U，假设包含n个数据对象，每个数据对象包含c维属性，要划分的簇的数目是k。

输出：聚类结果。

①计算数据集U中各维属性的权重系数jw。

②从数据集U中随机选取k个数据对象，作为初始聚类的中心点。

③按加权欧氏距离公式（6）计算其余各数据对象到聚类中心的距离，然后将各个数据对象划分到离它们最近的那个中心点所属类中。

④重新计算各个类的中心。

⑤比较与上次聚类的划分是否有变化，如果没变化，则聚类过程结束，输出聚类结果；否则，返回步骤③继续迭代，直到聚类划分不再改变。

加权欧氏距离，定义如下：

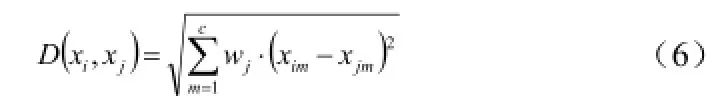
由此，我们可以得出改进K-means聚类算法的流程图如下所示：

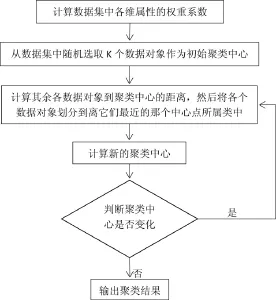
图1 聚类算法的流程图

2 实验及比较分析

实验数据集采用来自UCI数据集[7]中常用的2个聚类分析数据集iris和seeds。Iris数据集一共有150个数据，这些数据分为3类，每类分别包含50个数据，其中每个数据有4维属性。Seeds数据集一共有210个数据，这些数据分为3类，每类分别包含70个数据，其中每个数据有7维属性。

由于算法的初始中心点是随机选取，因此聚类结果不稳定。通过多次实验得到不同权重系数下最优的聚类结果。

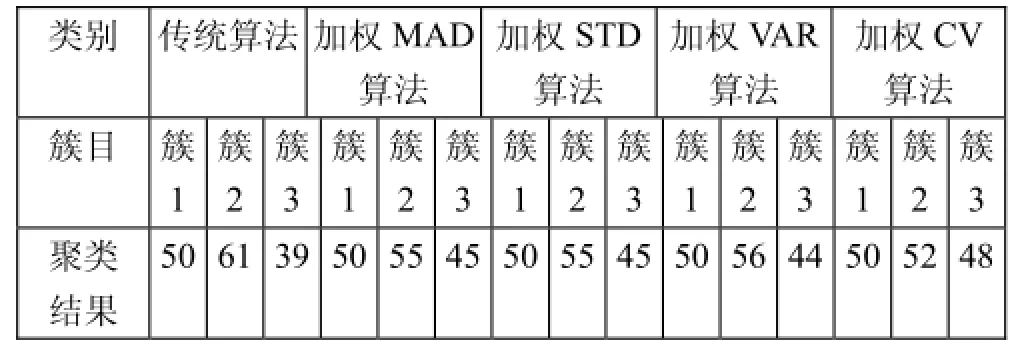
表1 iris数据集聚类结果比较

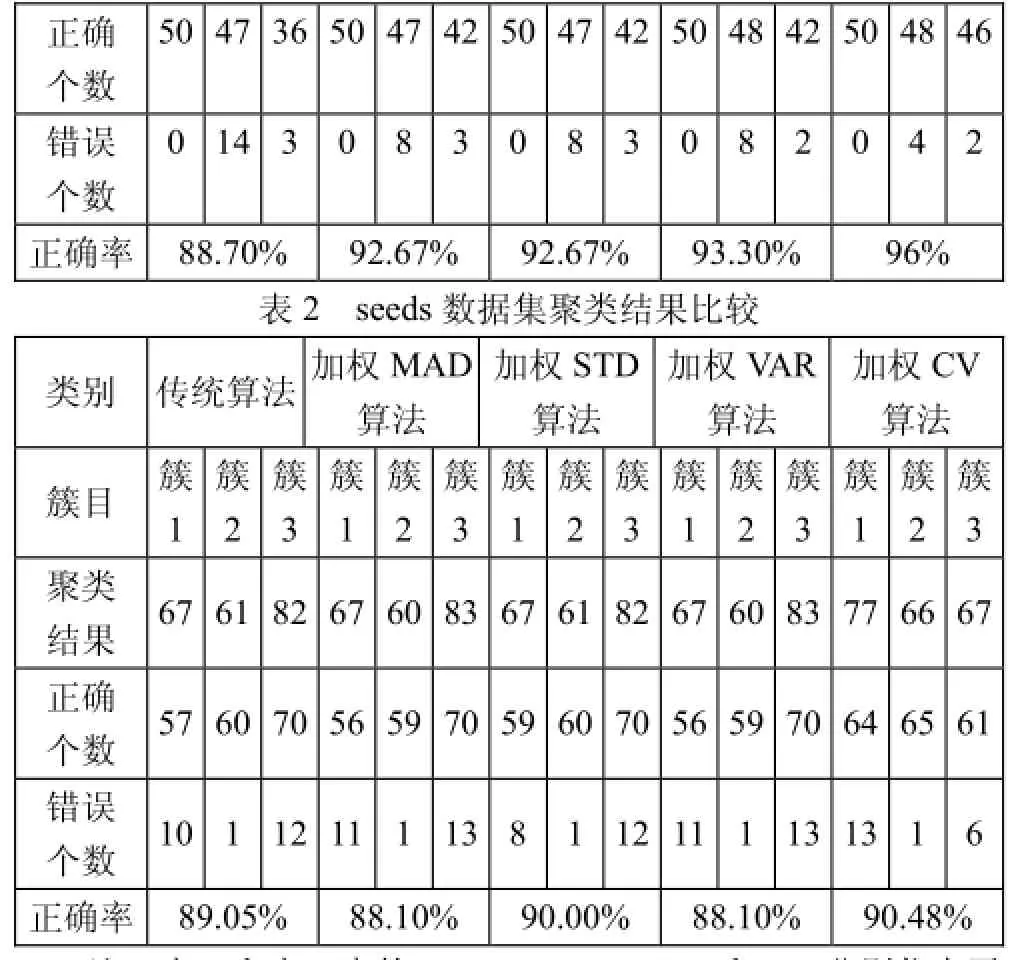
注：表1和表2中的MAD、STD、VAR和CV分别代表平均绝对偏差、标准差、方差和变异系数。

从表1中可以看出四种加权算法的正确率都比传统算法的高，而且以变异系数为加权系数使算法达到最高准确率。从表2中可以看到虽然以平均绝对偏差和方差为加权系数时准确率略有降低，但以标准差和变异系数为加权系数时准确率仍比传统算法高。

3 结束语

本文提出在K-means聚类算法中对欧氏距离进行加权的四种方法，并通过实验比较了四种加权方法的效果。实验结果表明在K-means聚类算法中对欧氏距离进行合理的加权可以提高聚类结果的准确率并且以变异系数为加权系数是一个简单有效的方法。相比其它的加权系数计算方法而言，这四种方法只依赖于要分析的数据本身，而不需要用户输入多余的参数，降低了用户的使用难度。

[1]Macqueen J．Some Methods for Classification and Analy sis of MultiVariate Observations[C]// Proc．of，Berkeley Sympo sium on Mathematical Statistics and Probability，1967．

[2]郑超，苗夺谦，王睿智．基于密度加权的粗糙K-均值聚类改进算法[J]．计算机科学，2009．

[3]王熙照，王亚东，湛燕，等．学习特征权值对K—均值聚类算法的优化[J]．计算机研究与发展，2003．

[4]陈森平，陈启买．基于熵的K均值算法的改进[J]．广东技术师范学院学报，2008．

[5]Sebastiani F．Machine Learning in Automated Text Cat egorization：a Bibliography[J]．Acm Computing Surveys，2002．

[6]冯荣耀，上官廷华，柳宏川．一种基于均方差属性加权的K-means算法[J]．信息技术，2010．

[7]Blake C L，Merz C J．UCI repository of machine lear ning databases[DB]．1998．http：//www．ics．uci．edu/mlearn /MLR epository．html．