基于遗传粒子滤波的轮毂驱动电动汽车质心侧偏角估计方法

孙传扬，张 欣，靳 彪

(北京交通大学 机械与电子控制工程学院，北京 100044)



基于遗传粒子滤波的轮毂驱动电动汽车质心侧偏角估计方法

孙传扬，张 欣，靳 彪

(北京交通大学 机械与电子控制工程学院，北京 100044)

质心侧偏角估计是汽车稳定性控制系统中的关键技术.为了解决现有估计方法对轮毂驱动电动汽车信息利用不充分、估计精度低的问题，提出一种基于遗传粒子滤波(GPF)的轮毂驱动电动汽车质心侧偏角估计方法.利用魔术轮胎公式，融合轮毂驱动电动汽车车轮上驱动与制动力矩信息,建立非线性车辆动力学模型，实现轮胎纵向力与侧向力计算，完成质心侧偏角估计器的搭建.针对车辆动力学模型的强非线性及传统粒子滤波算法粒子退化、计算量大的问题，设计适用于强非线性系统并且能够有效抑制退化、减小计算量的遗传粒子滤波算法对质心侧偏角进行估计.仿真结果表明: 所提出的估计方法能够提高质心侧偏角的估计精度和鲁棒性.

遗传粒子滤波；质心侧偏角估计；电动汽车；整车动力学模型

作为表征车辆稳定性的重要指标，质心侧偏角的实时估计是车辆稳定性控制系统的基础，其估计精度直接决定稳定性控制系统的效果[1].轮毂驱动电动汽车通过4个轮毂电机独立驱动，进一步提高了车轮的动态响应，改善了操控性和安全性[2].同时，轮毂驱动电动汽车能够在不增加传感器的情况下，通过轮毂电机获得准确的驱动力矩和车轮转速，为车辆状态估计提供准确的参考信息，从而提高估计的精度.

目前，关于质心侧偏角估计的方法已经有了较多的研究.文献[3]使用了扩展卡尔曼滤波方法(EKF)来估计车辆运动和轮胎力.通过忽略泰勒级数的高阶项实现了对非线性问题的处理，但同时也降低了估计的精度.文献[4]运用Unscented卡尔曼滤波(UKF)估计车辆运行状态参数，并表明UKF的滤波性能优于EKF.但是这两种方法都是基于高斯噪声的假设，而实际的环境噪声均非高斯噪声，因此运用该类方法的估计精度将会降低.

本文作者针对轮毂驱动电动汽车驱动力可测及系统强非线性的特点，提出了一种质心侧偏角估计方法.首先，搭建能够准确描述轮毂驱动电动汽车特点的非线性整车动力学模型；其次，利用魔术轮胎公式，融合轮毂电机的驱动力和转速信息计算轮胎力；最后，运用遗传粒子滤波算法建立非线性估计器，对质心侧偏角进行估计，并通过CarSim与Simulink的联合仿真实验验证算法的有效性.

1 整车动力学模型

传统的二自由度线性车辆模型中，假定车辆纵向车速不变，仅考虑横摆和侧向运动，不能准确描述实际行驶过程中车辆状态变量之间相互耦合的非线性关系.本文作者在横摆和侧向运动的基础上，考虑纵向运动，建立三自由度车辆动力学模型，描述车辆轴荷转移特性及单轮力学响应特性，如图1所示.图1中，车辆质心为CG；瞬时旋转中心为点O；r为旋转半径.

车辆模型的动力学方程为

其中：

(2)

式(1)和式(2)中：FXi和FYi(i=L1，L2，R1，R2，表示图中轮胎位置)分别为轮胎的纵向力和侧向力； FWX为风阻；FCP为向心力；mCG为整车质量；IZ为转动惯量；β为质心侧偏角；γ为横摆角速度；lF、lR分别为质心到前轴和后轴距离；lS为半轮距.向心力FCP可表示为

(3)

则质心侧偏角β可表示为

(4)

2 轮胎力计算

轮毂驱动电动汽车车轮驱动力矩可以通过电机力矩算得，且制动力矩可由制动轮缸压力算得.则车轮纵向力为

(5)

考虑汽车在转向过程中由于载荷转移引起的轮胎动载变化，从而导致侧向力具有较强的非线性特征，采用魔术公式计算轮胎侧向力.魔术公式通过三角函数的组合和大量实验数据，拟合轮胎非线性特性，能够准确描述车辆在极限工况下的轮胎力学特征.其计算公式为[5]

(6)

式中：i=L1，L2，R1，R2;BS为魔术轮胎公式的刚度系数；CS为形状系数;DS为峰值系数;ES为曲率系数;SVS、SHS为一般参数.

假设两前轮及两后轮的侧向滑移分别相同，轮胎侧偏角β为

(7)

将轮胎坐标系下的轮胎驱动力力FLi和轮胎侧向力FSi变换为车身坐标系下的力FXi和FYi，如图2所示.假设车辆为前轮转向，并且两前轮的转角一致.虽然在实际中两前轮转角并不完全相等，但是在本研究当中将这种差异忽略.

车辆前轮转角为δ，则前轴轮胎力可以转化为如下格式：

(8)

后轴轮胎力：

(9)

3 质心侧偏角估计器设计

3.1 估计模型设计

整理整车动力学模型与轮胎力计算模型，并考虑到横摆角速度易于测量的特点，将上述公式写成如下的状态空间模型形式：

(10)

可得状态方程为

(11)

量测方程为

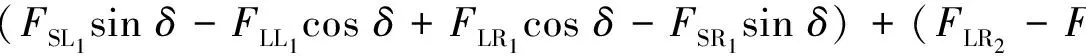
(FSR1+FSR2)lR+((FLR1+FLL1)cos δ+(FLR1+FLL1)sin δ)lF)+v

(12)

则状态向量x包括纵向车速、质心侧偏角和横摆角速度

x=[VXγ]T

(13)

输入向量u包括前轮转角和各轮胎力

u=[FLFLFLFRFLRLFLRR

FSFLFSFRFSRLFSRRδ]T

(14)

量测向量y为横摆角速度

y=[γ]

(15)

w、v分别为系统噪声和测量噪声，均为非高斯噪声，且两者互不相关.柯西-高斯混合模型(CGM)对环境噪声具有良好的拟合度，其概率密度函数(PDF)的具体表达式如下[6]：

fn(x)=(1-ε)fG(x)+εfC(x)=

(16)

3.2 遗传粒子滤波器设计

由于所建立的车辆动力学模型具有强非线性，使得线性高斯系统下求最优解的卡尔曼滤波方法不再适用.

遗传粒子滤波(GPF)算法针对传统粒子滤波算法中存在的粒子退化和计算量大的问题，采用遗传算法中的选择、交叉、变异进化思想，代替了重采样方法，提高了算法性能.遗传算法独特的寻优能力，可以提高粒子的使用效率，从而减少了所需的粒子数，避免了重采样，在一定程度上减小了计算量，有效提高了算法的实时性，且有效增加粒子的多样性，解决粒子退化问题，有效防止出现滤波发散现象，从而提高了状态估计精度.其具体步骤如下.

1)离散化.采用经典龙格库塔方法将状态空间模型离散化为如下形式

(17)

式中:x(k)、y(k)、u(k)、w(k)、v(k)为k时刻向量.

3)权值更新.在k时刻，更新粒子权值

i=1,2,…,Ns

(18)

为便于实现，选择先验概率密度作为重要密度函数，即

i=1,2,…,Ns

(19)

则重要性权值简化为式(20),归一化成式(21)

(20)

(21)

4)遗传操作

(22)

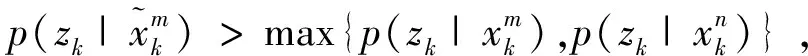
(23)

5)状态估计并输出.

(24)

4 仿真结果分析

应用汽车动力学仿真软件CarSim对设计的质心侧偏角估计方法进行验证.CarSim是采用实际车辆的数据仿真驾驶员、路面及车辆动力学输入的响应，可用于功能开发、控制系统测试及算法验证.

本文设置CarSim中的车辆参数及运行工况，输出模型所需的方向盘转角δ和各轮转速ω，与Simulink联合仿真，实现质心侧偏角的估计，验证GPF算法的有效性.图3为基于CarSim和Simulink的联合虚拟仿真平台.

在CarSim仿真平台中，参照ISO3888-2双移线试验标准进行了仿真实验，分别在两种不同的车速和路面下进行，车辆前轮转角如图4所示.

为考察GPF算法对非线性车辆系统的估计性能，将其估计值与标准粒子滤波算法(PF)估计值及CarSim仿真值进行对比，如图5所示.

在粒子数均为200时，GPF的计算效率明显优于PF算法，运行时间由2.03 s缩短到1.83 s.验证参数如下：lF为1.016 m；lR为1.564 m;IZ为1 536.7 kgm2;mCG为1 341 kg;轮距2lS为1.54 m.

由图5(a)可知，当车辆初始速度为120 km/h、路面附着系数为0.85时，转向过程中轮胎仍处于线性区域，质心侧偏角变化较小，GPF算法和PF算法都能够很好的跟随仿真值.由图5(b)可知，当车辆初始速度为50 km/h、路面附着系数为0.4时，由于轮胎模型与实际轮胎力学特性的差异及汽车模型的局限性，在峰值段的强非线性区域，估计值存在一定的偏差.但是整个过程中，GPF算法的估计结果与PF算法的估计结果相比更接近仿真值.

5 结论

1)利用轮毂驱动电动汽车驱动力矩可获得的特点，结合魔术公式，对轮胎力进行计算，并作为估计模型的输入量，提高了模型的估计精度.

2)针对传统滤波方法无法解决非线性、非高斯车辆系统的参数估计问题，提出基于遗传粒子滤波算法的质心侧偏角估计方法，该方法能够在多工况下准确估计质心侧偏角.

3)针对粒子退化和重采样带来的计算量大的问题，遗传粒子滤波通过交叉、变异等遗传操作增加了粒子的多样性，提高了计算效率.

[1] 陈慧,高博麟,徐帆. 车辆质心侧偏角估计综述[J]. 机械工程学报,2013,49(24):76-94. CHEN Hui, GAO Bolin, XU Fan. Review on vehicle sideslip angle estimation[J]. Journal of Mechanical Engineering,2013,49(24):76-94.(in Chinese)

[2] 靳彪,张欣,杨庆保. 纯电动汽车低速转向差速控制模型[J]. 北京交通大学学报,2013,37(4):158-161. JIN Biao, ZHANG Xin, YANG Qingbao. Low speed steering differential control model for pure electric vehicle[J]. Journal of Beijing Jiaotong University, 2013, 37(4): 158-161. (in Chinese)

[3] 宗长富,潘钊,胡丹,等. 基于扩展卡尔曼滤波的信息融合技术在车辆状态估计中的应用[J]. 机械工程学报,2009,45(10):272-277. ZONG Changfu, PAN Zhao, HU Dan, et al. Information fusion algorithm for vehicle state estimation based on extended kalman filtering[J]. Journal of Mechanical Engineering, 2009,45(10):272-277.(in Chinese)

[4] 解少博,林程. 基于无迹卡尔曼滤波的车辆状态与参数估计[J]. 农业机械学报,2011,42(12):6-12. XIE Shaobo, LIN Cheng.State and parameters estimation of vehicle based on UKF[J]. Transactions of the Chinese Society for Agricultural Machinery, 2011,42(12):6-12.(in Chinese)

[5] PACEJKA H B,BAKKER E.The magic formula tyre model[J].Vehicle System Dynamics,1992,21(S1):1-18.

[6] LI X T, CHEN Z T, WANG S Y. An approximate representation of heavy-tailed noise: bi-parameter Cauchy-Gaussian mixture model[C]// Proceedings of 9th Signal Processing, 2008: 76-79.

Vehicle body side slip angle estimation based on genetic particle filter for in-wheel-motored electric vehicle

SUNChuanyang,ZHANGXin,JINBiao

(School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, Beijing 100044,China)

Vehicle body side slip angle (VBSSA) estimation is the key technology of vehicle dynamics control systems. In order to overcome the problems in existing estimation methods such as information used insufficiently and low accuracy, a VBSSA estimation method based on genetic particle filter (GPF) for in-wheel-motored electric vehicle is proposed. Given that the torque information of in-wheel-motored electric vehicle is available, tire forces can be generated based on the Magic Formula tire model. The observer of VBSSA is constructed based on the nonlinear vehicle dynamic model. The GPF is introduced to solve the VBSSA estimation problem in nonlinear conditions, and alleviate the problems of particle degradation and large amount of calculation. Simulation results show that the proposed method can improve the accuracy and robustness of VBSSA estimation.

genetic particle filter; vehicle body side slip angle estimation; electric vehicle; vehicle dynamics model

1673-0291(2016)06-0102-05

10.11860/j.issn.1673-0291.2016.06.017

2016-01-25

中央高校基本科研业务费专项资金资助(M15JB00210)

孙传扬(1992—)，男，山东日照人，博士生.研究方向为整车动力学控制.email:14116369@bjtu.edu.cn.

U469. 72

A