Adaptive Image Zooming Algorithm Combining Total Variation Minimization and a Second-order Functional

(College of Science,Zhongyuan University of Technology,Zhengzhou450007,China)

Adaptive Image Zooming Algorithm Combining Total Variation Minimization and a Second-order Functional

WANG Yan-yan,GAO Ran,GU Cong

(College of Science,Zhongyuan University of Technology,Zhengzhou450007,China)

An image zooming algorithm by using partial diferential equations(PDEs)is proposed here.It combines the second-order PDE with a fourth-order PDE.The combined algorithm is able to preserve edges and at the same time avoid the blurry efect in smooth regions.An adaptive function is used to combine the two PDEs.Numerical experiments illustrate advantages of the proposed model.

adaptive image zooming;total variation;PDEs

§1.Introduction

An approach to obtain a zoomed imageufrom the sampling imageu0is proposed in this work.Digital image can basically be decomposed into three distinguished areas:fat regions, regions with a smooth change in the intensity value,and jumps.The aim of all image zooming methods is to keep the fat regions and enhance these characteristics.Unfortunately,all the methods we known,can preserve the low frequency content of the source image well,but are not equally well to enhance high frequencies in order to produce an image whose visual sharpness matches the quality of the original one.Especially,when the image is zoomed by a large factor, the zoomed image looks very often blocky[12].

Total Variation(TV)minimization is a successful approach to recover images with sharp edges.This method was proposed by Rudin,Osher and Fatemi(ROF)in[3],the TV functionalas following

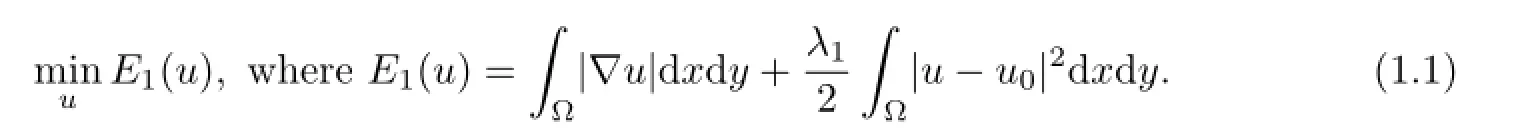
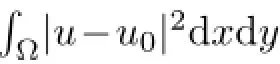
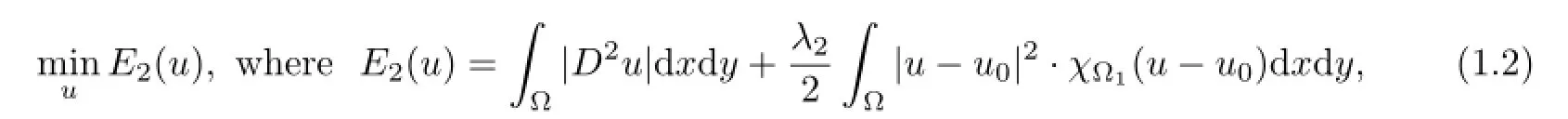
whereχΩ1is the characteristic function of Ω1,(x,y)∈Ω1is a pixel of the original image,λ2＞0 balances the two terms.Higher-order PDEs are known to recover smoother surface,but it seems to be hard to get one method to preserve discontinuities in one part of the image and simulataneously recover smooth signals in other parts.Hence,our approach is to involve both a lower-and higher-order PDE.

The paper is organized as follows.Our PDE-based model and its numerical realization are formally introduced in Section 2.Section 3 is devoted to numerical experiments,followed by some conclusions in Section 4.

§2.The Combined Image Zooming Algorithm and Its Realization

2.1The PDE-based Model

To formulate the problem in the continuous setting,we assume that the low resolution imageu0(x,y)=v0(x,y),(x,y)∈Ω1is given in Ω1⊂Ω.In the discrete setting,Ω1contains the grid points of the low resolution image pixels.From the values ofu0∈Ω1,we want to extend them to the whole region.

For this purpose,we shall try to fnd the functionu,vdefned respectively in the whole region to minimize the energy functional as following

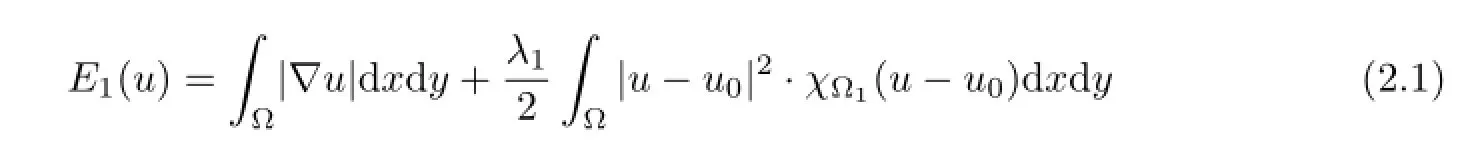
and

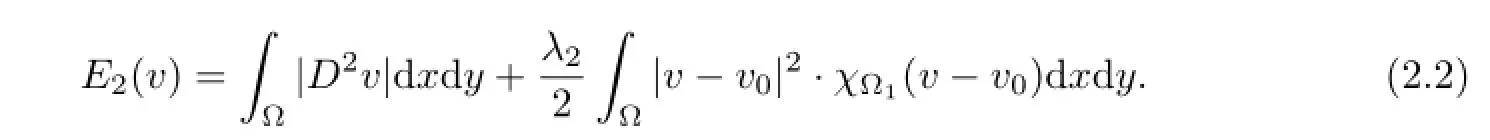
The frst term inE1(u),E2(v)is a smoothing term and it is used to guarantee that recovered image has smooth level curves.The parameterλ1,λ2are positive weighting constants thatcontrol contribution of fdelity term.Minimizing the two continuous energy functional yields nonlinear second-order PDE and a fourth-order PDE.From the Euler-Lagrange variational principle,the minimizer ofuand the minimizer ofvcan be interpreted as the steady solution of the nonlinear difusion process

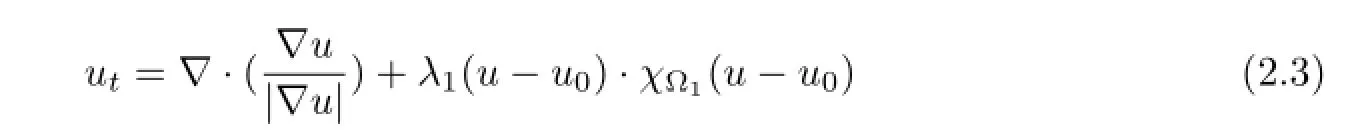
and

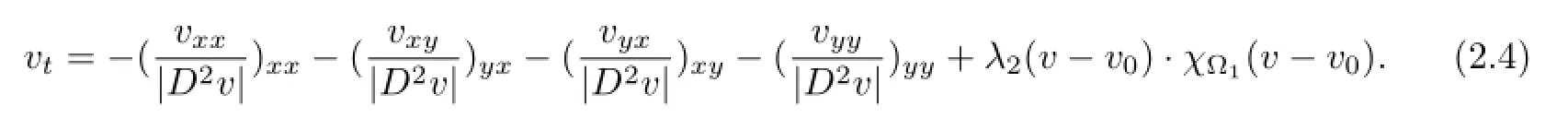
Thereby,we obtain two PDE-based interpolation models.Both methods have their strengths and weaknesses depending on the characteristics of the image of interest.Because of this,we combine the two methods to generate a new solution by taking the best from each other.

2.2The Combined Model and Implementation Details

The new energy functional built as following

wherethe image gradient value is bigger on the edge of the image,nowthe model close to second-order PDE;the image gradient value is smaller on the smooth regions,at this pointthe model close to fourth-order PDE model.

Using the variational method to solve the above model,we get the Euler-Lagrange equation

Namely

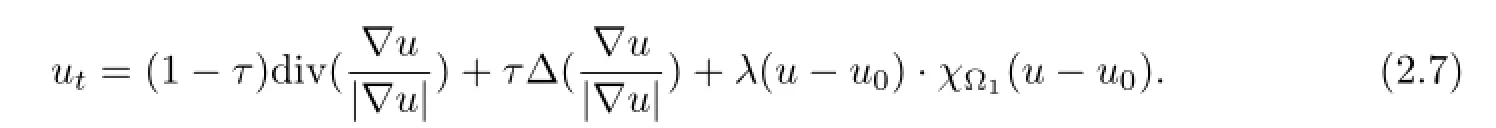
The details of the algorithm we have used are given in the following.

AlgorithmWe assume initial image matrixT0ism×n.

(1)By sampling to reducek(kis a positive integer)times in order to getT′,assigningT′toTand then using linear interpolation forT(this paper adopts three cubic interpolation),fnally, we get the matrixu0which is to be magnifed forktimes;

(2)We fndu(the purpose of the image zooming)by(2.7)and update the solution by

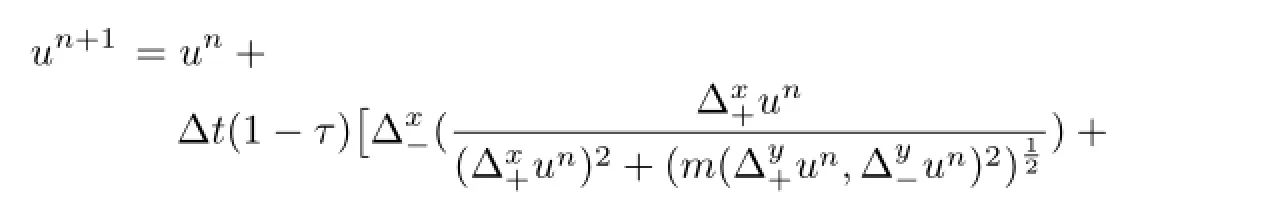
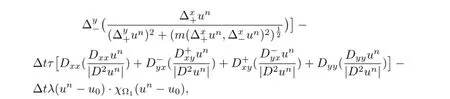
whenunhas reached a steady state,it is taken as the zoomed image.

§3.Numerical Experiments

Several experiments with the proposed algorithm have been performed.We present a few of them in this section.We present our experimental results for images such as“Cameraman”and“Lena”,see fgures 1～2.

Fig 1 Cameraman Image Zoomed by Twice

Fig 2 Lena Image Zoomed by Twice

It’s known that with large Δt,the iterations will converge faster.But if they are too large, the scheme will be unstable and will not converge to a steady state.It is then necessary to choose a reasonable smaller time step.It is usual to choose Δtby trial and error based on our experience.For most experiments,we always use fxed time step Δt=10-3.We chose Δx=Δy=1 and the parameterλis set equal to 0.5.

We usually observe the quality of a zoomed image by visual examinations.However,in order to use the subjective standards to show the efciency of our algorithm,Peak Signal-to-Noise Ratio(PSNR)and Mean Squared Error(MSE)[10]are also used here to measure the image quality.The PSNR and MSE are defned as

Here,(M,N)is the size of original high-resolution image,u0,uare the original and zoomed images respectively.We give some values of PSNR and MSE in the fouowing table.The data is obtained when the original images are zoomed by a factor of 2.As shown in the table1,our algorithm improves the PSNR and MSE for all cases and all the data are obtained when the energy functional has been stabilized.The improvement of PSNR is great for gray-scale images.

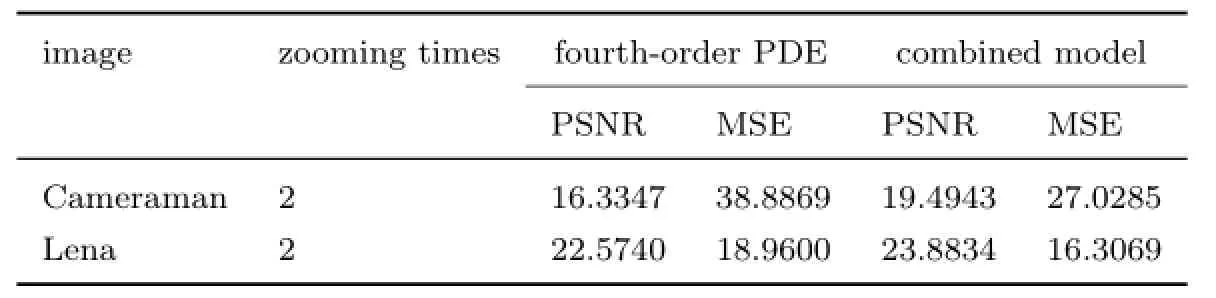
PSNR and MSE of the Diferent Model

Many image zooming techniques sufers from the so called“checkerboard efect”.By comparing the efects of several methods in fgures 1-2,can be seen that fourth-order PDE model this efect is not obvious,but the image is fuzzy;our algorithm can faithfully refected the primitive appearance of the original images,and maintained the edge sharpness and the texture characteristic,showing that our algorithm obtains better visual impression.

§4.Conclusion

In this paper,we proposed an image zooming method based on nonlinear PDEs.Anisotropic difusion has been incorporated through the numerical discretization of the model.The proposed algorithm is able to locate discontinuities as accurate ad the ROF algorithm,and at the same time do a better job in regions with a smooth variation.All the examples indicate that our algorithm is efcient for image zooming and has good subjective quality.Due to the complexity of the equations involved,it is not easy to supply a theoretical verifcation for this.

[1]YUAN Qiu-qi,WU Ji-ying.Partial diferential equation method on digital image processing[J].Signal processing,2012,28(3):301-314.

[2]KIM H,CHA Y,KIM S.Curvature interpolation method for image zooming[J].IEEE Transactions on Image Processing,2011,20(7):1895-1903.

[3]RUDIN L,OSHER S,FATEMI E.Nonlinear total variation based on noise removal algorithms[J].Physica D,vol.1992,60:259-268.

[4]LYSAKER M,LUNDERVOLD A,TAI X C.Noise removal using fourth-order partial diferential equation with applications to medical magnetic resonance image in space and time[J].IEEE Transactions on Image Processing,2003,12(12):1579-1590.

[5]LYSAKER M,LUNDERVOLD A,TAI X C.Noise removal using smoothed normals and surface ftting[J]. IEEE Transactions on Image Processing,2004,13(10):1345-1357.

[6]GREER J B,BERTORRI A L.Travling wave solutions of fourth order PDEs for image processing[J].SIAM Journal on Mathematical Analysis,2004,36(1):38-68.

[7]BERRRITO A L,GREER J B.Low-curvature image simplifers:global regularity of smooth solutions and Capalacian liniting schemes[J].Communications on Pure&Applied Mathematics,2004,57(6):764-790.

[8]GAO Ran,SONG Jin-ping,TAI Xue-cheng.Image zooming algorithm based on partial diferential equations technique[J].International Journal of Numerical Analysis and Modeling,2009,6(2):284-292.

[9]MARIUS LYSAKER,TAI Xue-cheng.Iterative image restoration combining total variation minimization and a second-order functional[J].International Journal of Computer Vision,2006,66(1):5-18.

[10]LI Peng,ZOU Yang,YAO Zheng-an.Fourth-order anisotropic difusion equations for image zooming[J]. Journal of Image and Graphics,2013,18(10):1261-1269.

O175.2

:A

1002–0462(2016)04–0435–06

Received date:2016-05-26

Foundation item:Supported by the National Nature Science Foundation of China(11401604);Supported by the Natural Science Foundation of Henan Province(142300410354,142300410355,152300410226,152300410227); Supported by the Science and Technology Projects of Henan Provincial Education Department(15A110045, 17A110036)

Biography:WANG Yan-yan(1964-),female,native of Kaifeng,Henan,an associate professor of Zhongyuan University of Technology,M.S.D.,engages in PDEs.

2000 MR Subject Classifcation:68U10