When is an Almost Locally Compact Space Supercomplete?

(School of Mathematics and Statistics,Minnan Normal University,Zhangzhou363000,China)

When is an Almost Locally Compact Space Supercomplete?

LI Xiao-ting,LIN Fu-cai

(School of Mathematics and Statistics,Minnan Normal University,Zhangzhou363000,China)

It is proved in this paper that(1)the topological sum of a family of supercomplete spaces is supercomplete;(2)ifXis a metacompact and almost locally compact space thenXis supercomplete.Moreover,some questions on supercomplete spaces are posed in the paper.

supercomplete spaces;sums of topological spaces;almost locally compact; metacompact spaces

§1.Introduction

Throughout this paper all spaces are assumed to be Tychonof,and all maps are continuous and onto.The letters N and R will denote the set of positive integer numbers and the set of real numbers,respectively.Readers may refer to[6-7]for unstated defnitions and terminologies.

Defnition 1.1LetXbe a space.

(1)The spaceXis calledˇCech complete if it is aGδ-set in one of its Hausdorfcompactifcations[5];

(2)The spaceXis called ultracomplete[1]if there is a countable collection{Gn:n∈N}of open covers ofXsatisfying the property that whenever F is flter onXsuch that for eachn∈N there is someGn∈Gnwhich meets all the members of F,then F has a cluster point.

It is well known that every ultracomplete space isˇCech complete,however the implication is not reversible.Ultracomplete spaces are also called cofnallyˇCech complete[3].

In[4],D Buhagiar and B A Pasynkov introduced the notion of supercomplete spaces because this class spaces are interesting and important for characterizing bothˇCech complete and ultracomplete spaces[1],and proved that(1)every supercomplete space isˇCech complete, but the converse is not true in general;(2)the ultracompleteness implies supercompleteness in the theory of uniformities.However,the notions of ultracompleteness and supercompleteness are non-comparable in the topological case.[10]is the continuous study of[4],where F C Lin and R C Shen introduced the notion of c-U-supercomplete of a spaceXand proved that a metacompact space is locally compact if and only if it is c-U-supercomplete.

Defnition 1.2[4]Let U={Un:n∈N}be a sequence of open covers of a topological spaceX.A family F of subsets ofXis called U-stable if,for anyn∈N,there existsFn∈F such thatFn⊂St(F,Un)for anyF∈F.

Obviously,for a flter F,the last condition may be formulated in the following way

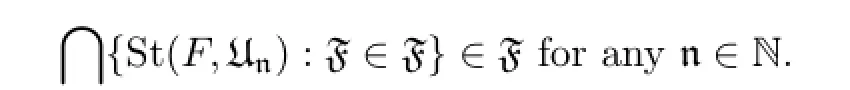
Defnition 1.3[4]A spaceXis called supercomplete if there exists a sequence U={Un: n∈N}of open covers ofXsuch that every U-stable flter F has a cluster point inX.Moreover, we call U is a supercomplete sequence of open covers of the spaceX.

Defnition 1.4[4]A spaceXis called supercomplete with respect to an open coverUofX(U-supercomplete,for short)if the sequence U={U〉=U:〉∈N}is supercomplete.

Defnition 1.5[10]A spaceXis called c-supercomplete with respect to an open coverUofX(c-U-supercomplete,for short)if for any closed flterFforX,there exists anF∈Fsuch thatF⊂St(F′,U)for anyF′∈F,thenFhas a cluster point inX.

It is easy to see that

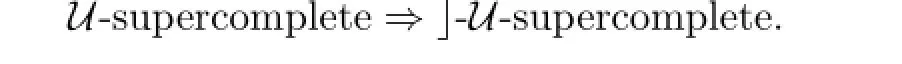
In section 1,we shall prove that the topological sum of a family of supercomplete spaces is supercomplete;In section 2,we shall prove that a metacompact and almost locally compact space is supercomplete.

§2.Sums of Supercomplete Spaces

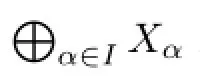
ProofWe only show the case of the supercompleteness since the cases of c-U-supercompleteness and U-supercompleteness are similar.Moreover,without loss of generality,we may assume thatXα∩Xβ=Øfor eachα/=β.

Sufciency.For everyα∈I,let Uα={Uαn:n∈N}be a supercomplete sequence of open covers of the spaceXα.PutSfor everyn∈N.Then V={Vn:n∈N}is a supercomplete sequence of open covers of

Corollary 2.2LetXbe a supercomplete(resp.,c-U-supercomplete,U-supercomplete) space.ThenX×Yis a supercomplete space(resp.,c-U-supercomplete,U-supercomplete), whereYis endowed with discrete topology.

ProofLetFor eachα∈∧,sinceit follows thatX×{yα}is supercomplete.Thenis supercomplete by Theorem 2.1.Sincethe spaceX×Yis supercomplete.

§3.Almost Locally Compact Supercomplete Spaces

LetXbe a space andX0be the set of all points of non-local compactness ofX.The spaceXis called almost locally compact[8]ifX0is contained in a compact subset of countable outer character inX.Obviously,locally compact spaces are almost locally compact.

There exists a locally compact and non-supercomplete space,such as[0,ω1).Hence we have the following question.

Question 3.1When is a locally compact or almost locally compact space supercomplete?

A topological spaceXis said to be metacompact if every open cover has a point fnite open refnement.

Next we give a partial answer to Question 3.1.

Theorem 3.2LetXbe a metacompact and almost locally compact space.ThenXis supercomplete.

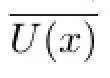
For eachn∈N,sinceXis metacompact,there exists a point-fnite open cover Vnrefning Mn. Put

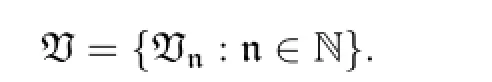
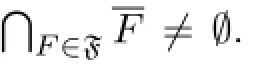
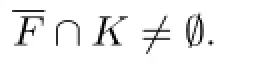
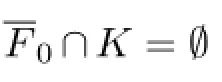
which is a contradiction.

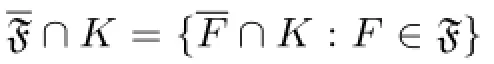
Corollary 3.3LetXbe a metacompact and locally compact space.ThenXis supercomplete.

Defnition 3.4LetXbe a space.

(1)The spaceXis called isocompact if every countably compact subspace ofXis compact;

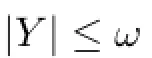
LetXbe a space andA⊂X.The subspaceAis said to beboundedinXif every continuous real-valued function onXis bounded onA.Namely,the collectionis fnite for every discrete subcollection.Let

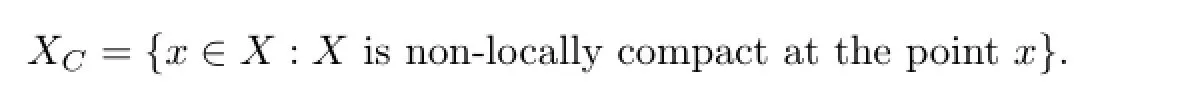
Remark(1)In[9],D Jard´on and V V Tkachuk proved that,for an isocompactωmonolithic spaceX,the spaceXis ultracomplete if and only ifXis almost locally compact. However,There exists an isocompactω-monolithic supercomplete space,which is non-almost locally compact.Indeed,letXbe the set of irrational points of R and endowXwith the subspace topology of R.ThenXis aˇCech-complete metrizable space[6]and henceXis su-percomplete.Moreover,it is easy to see thatXis isocompactω-monolithic.However,Xis nowhere locally compact and non-compact,and henceXis non-almost locally compact.

(2)In[2],A G M´aynez and S Romaguera proved thatXCis bounded in an ultracomplete space.However,there exists a supercomplete spaceXsuch thatXCis not bounded.Indeed,letXbe the set of irrational points of R and as a subspace of R.ThenXis a supercomplete space, and it follows from[2]that it is non-ultracomplete.SinceXis non-almost locally compact,the spaceXis non-locally compact.LetY=X×N,where N is endowed with discrete topology. ThenYis supercomplete by Corollary 2.2.SinceXis non-locally compact,it follows thatYC/=ØandYC=XC×N.Put B={X×{n}:n∈N}.Then B is a discrete open family ofY.However,we haveB∩YC/=Øfor eachB∈B.ThusYCis not bounded.

Therefore,we have the following two questions.

Question 3.6When is a supercomplete space locally compact or almost locally compact?

Question 3.7Can we give a necessity and sufciency condition for a supercomplete spaceXsuch thatXCis bounded?

[1]CS´ASZ´AR ´A.Strongly complete,supercomplete and ultracomplete spaces[J].Mathematical Structures-Computational Mathematics-Mathematical Modelling,Papers dedicated to Prof L Iliev’s 60th Anniversary (Sofa),1975:195-202.

[2]GARC´IA-M´AYNEZ A,ROMAGUERA S.Perfect pre-images of cofnally complete metric spaces[J].Comment Math Univ Carolinae,1999,40(2):335-342.

[3]BUHAGIAR D,YOSHIOKA I.Ultracomplete topological spaces[J].Acta Math Hungar,2001,92:19-26.

[4]BUHAGIAR D,PASYNKOV B A.Supercomplete topological spaces[J].Acta Math Hunger,2007,115(4): 269-279.

[5]ˇCECH E.On bicompact spaces[J].Ann of Math,1937,38:823-844.

[6]ENGELKING R.General Topology[M].Berlin:Heldermann Verlag,1989.

[7]GRUENHAGE G.Generalized Metric Spaces,in:Handbook of Set-theoretic Topology[M].Amsterdam: Elsevier Science Publishers B V,1984:423-501.

[8]JARD´ON D,TKACHUK V V.Ultracompleteness in Eberlein-Grothendieck spaces[J].Bol Soc Mat Mex, 2004,10(3):209-218.

[9]JARD´ON D,TKACHUK V V.When is an ultracomplete space almost locally compact[J].Applied Gen Topol,2006,7(2):191-201.

[10]LIN Fu-cai,SHEN Rong-xin.A note on supercomplete spaces[J].Acta Math Hungar,2009,123(3):229-232.

O189.11

:A

1002–0462(2016)04–0430–05

Received date:2015-03-27

Foundation item:Supported by the National Natural Science Foundation of China(11201414,11571158, 11171162);Supported by the Natural Science Foundation of Fujian Province(2012J05013);Supported by the Training Programme Foundation for Excellent Youth Researching Talents of Fujian’s Universities(JA13190)

Biographies:LI Xiao-ting(1990-),female,native of Huizhou,Guangdong,M.S.D.,engages in general topology;LIN Fu-cai(1979-),male,native of Quanzhou,Fujian,an associate professor of Minnan Normal University, Ph.D.,engages in general topology.

2010 MR Subject Classifcation:54C10,54D55,54E40