Stability of Neutral Fractional Neural Networks with Delay

LI Yan,JIANG Wei2,HU Bei-bei

(1.School of Institute of Mathematics and Finance,Chuzhou University,Chuzhou239000,China;2.School of Mathematical Science,Anhui University,Hefei230601,China)

Stability of Neutral Fractional Neural Networks with Delay

LI Yan1,JIANG Wei2,HU Bei-bei1

(1.School of Institute of Mathematics and Finance,Chuzhou University,Chuzhou239000,China;2.School of Mathematical Science,Anhui University,Hefei230601,China)

This paper studies stability of neutral fractional neural networks with delay.By introducing the defnition of norm and using the uniform stability,the sufcient condition for uniform stability of neutral fractional neural networks with delay is obtained.

fractional;delay;stability

§1.Introduction

Fractional calculus was frstly introduced 300 years ago,which mainly deals with derivatives and integrals of arbitrary order.Fractional diferential equations have gained increasing attention because of their varied applications in various felds of applied sciences and engineering.Its applications to physics and engineering are just a recent focus of interest to many researchers. Compared with the classical integer-order systems,fractional-order systems provide an excellent instrument for the description of memory and hereditary properties of various materials and processes[14].Nowadays,studying on fractional-order calculus has become an active research feld.

As we know,compared with the classical integer-order models,fractional-order derivatives provide an excellent instrument for the description of memory and hereditary properties of various materials and processes.Therefore,it may be more accurate to model by fractional-orderderivatives than integer-order ones.In recent years,fractional operator is introduced into artifcial neural network,such as Arefeh Boroomand and Mohammad B Menhaj’s fractional-order hopfeld neural networks[5].The univariate fractional quantitative approximation of real valued functions on a compact interval by quasi-interpolation sigmoidal and hyperbolic tangent neural network operators is studied[6].It is important to note that fractional-order recurrent neural networks might be expected to play an important role in applications.The projective synchronization of fractional-order memristor-based neural networks is investigated[7].Therefore, whatever in the area of theoretical research or in practical application,to study fractional-order neural networks is very necessary and positive.

It is well known stability analysis,such as Lyapunov stability,is one of central tasks in the study of fractional diferential systems.Stability of neural networks has been widely investigated and excellent results have been obtained.In recent years,there have been some advances in stability theory of fractional diferential systems.For instances,stability and multi-stability (coexistence of several diferent stable states).The global asymptotic stability for Hopfeld neural networks with time delay was investigated[8].Dynamic analysis of a class of fractionalorder neural networks with delay[9].Until now,there are many valuable results about stability of fractional neural networks[1015].Along with the development of electronic technology,it was found that sometimes need to consider not only the past state infuence on now,but also consider the infuence of the state of the change of state of the past to now,this is neutral delay. Most of which are discussing stability analysis of fractional-order neural networks,but these results and methods could not be extended and applied to fractional-order case.Therefore, to establish some stability of neutral fractional neural networks with delay is necessary.This paper studies stability of neutral fractional neural networks with delay.By introducing the defnition of norm and using the uniform stability,the sufcient condition for uniform stability of neutral fractional delay neural networks is obtained.

The rest of the paper is organized as follows.In Section 2 some basic defnitions of fractional calculus used in this paper are mentioned.Section 3 the main results are shown.Finally,some conclusions are drawn in Section 4.

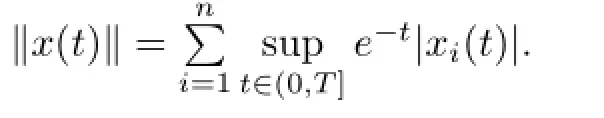
§2.Model Description and Preliminaries

In this section,some basic defnitions and lemmas are introduced,which will be used in the following discussions.

Defnition 1Riemann-Liouville’s fractional integral with orderα＞0 of continuous functionx(t)is defned as

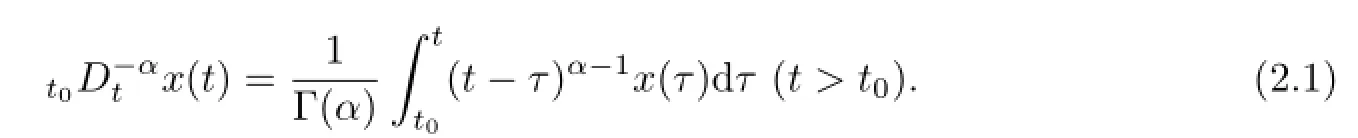
Defnition 2The(left-sided)Caputo derivatives with orderαof functionx(t)∈Cn([t0,+∞),R)is defned as

wheret＞t0andnis a positive integral such thatn-1＜α＜n.

Lemma 1Ifx(t)∈Cm[0,∞)andm-1＜α＜m∈z+,then

The dynamic behavior of a continuous neural fractional-order delayed neural network can be described by the following diferential equation

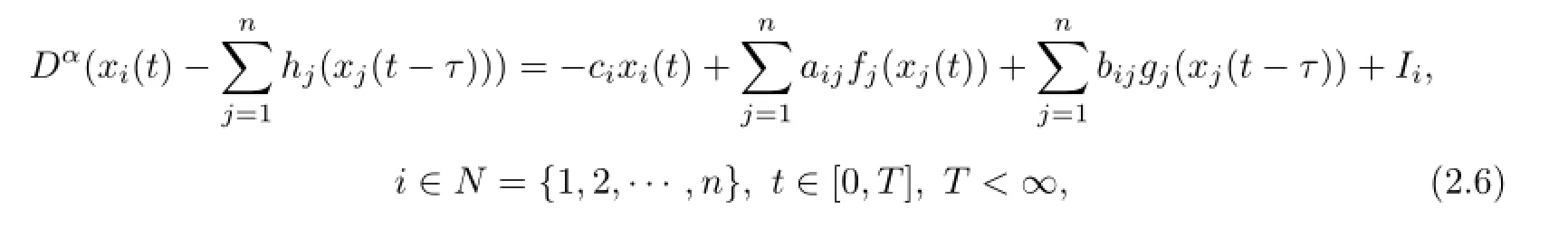
or equivalently

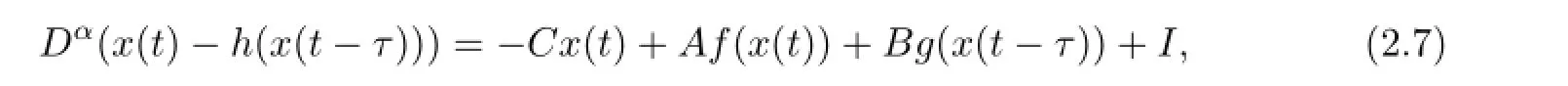
where 0＜α＜1.ncorresponds to the number of units in a neural network,x(t)=(x1(t),···, xn(t))T∈Rncorrespondstothestate vector at timet;f(x(t))=(f1(x1(t)),f2(x2(t)),···,fn(xn(t)))T,g(x(t))=(g1(x1(t)),g2(x2(t)),···,gn(xn(t)))Tandh(x(t))=(h1(x1(t)),h2(x2(t)),···, hn(xn(t)))Ta denote the activation function of the neurons;C,A,Bare constant matrices;C=diag(ci＞0)represents the rate with which theith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs.A={aij}andB={bij}are referred to the connection of thejth neuron to theith neuron at timetandt-τ, respectively,whereτis the transmission delay and a nonnegative constant.I=(I1,I2,···,In)Tis an external bias vector.

The initial conditions associated with system(2.6)are of the form

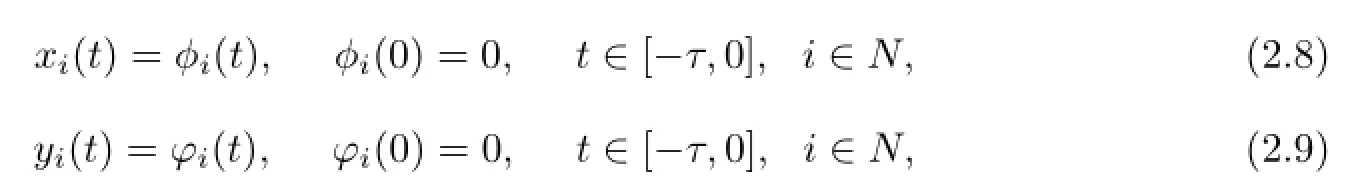
where it is usually assumed thatφi(s)∈C([-τ,0],R),i∈Nand the norm ofC([-τ,0],R)is denoted by

Defnition 3The solution of system(2.6)is said to be stable if for anyε＞0 there existsδ(t0,ε)＞0 such thatt≥t0≥0,‖φ(t)-φ(t)‖＜δimply‖y(t,t0,φ)-x(t,t0,φ)‖＜εfor any two solutionx(t,t0,φ)andy(t,t0,φ).It is uniformly stable(US)if the aboveδis independent oft0.

Here we make the following assumptions in order to obtain the main results.

Assumption 1The neuron activation functionfj,gj,hjare Lipschitz continuous.That is,there exist positive constantsFj,Gj,Hj(j=1,2,···,n)such that

Assumption 2ci,aij,bij,FjandGjsatisfy the following condition

§3.Main Results

In this subsection,we derive the sufcient condition for uniform stability of neutral fractional delay neural networks.

Theorem 1If assumptions(A1)and(A2)hold,then the system(2.6)is uniformly stable.

ProofAssume thatx(t)=(x1(t),···,xn(t))Tandy(t)=(y1(t),···,yn(t))Tare any two solution of(2.6)with the diferent initial conditionxi(s)=φi(s)∈C([-τ,0],R),φi(0)=0,yi(s)=φi(s)∈C([-τ,0],R),φi(0)=0,i∈N,one has

Based on Lemma 1,the solution of the system(2.6)can be expressed in the following form

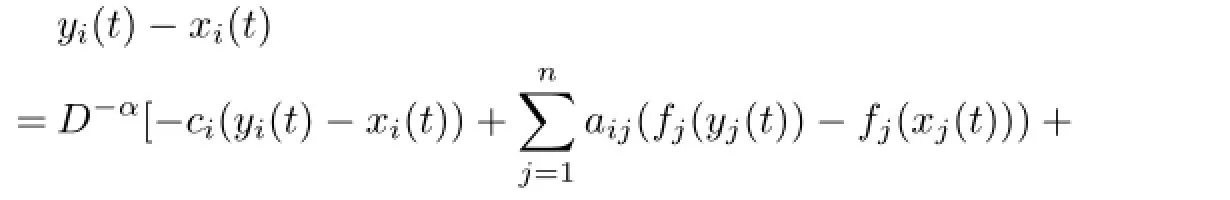
Then

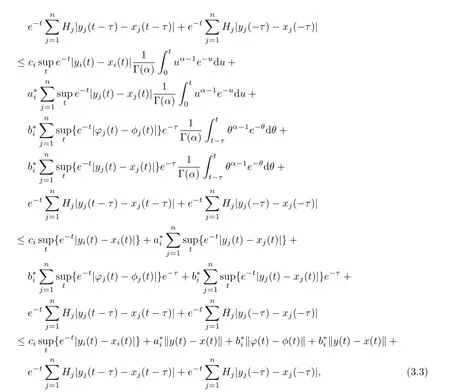
we obtains

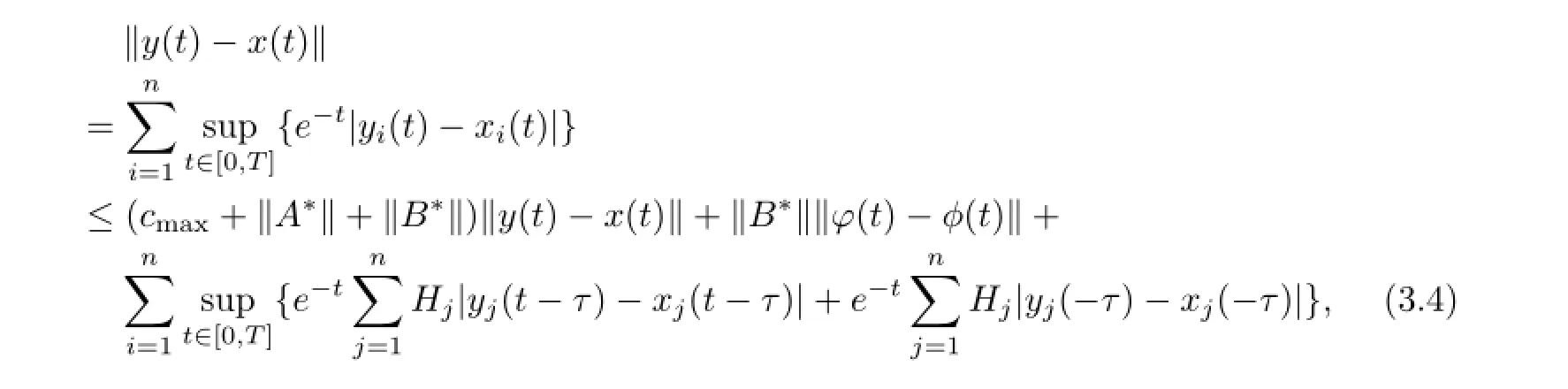
where

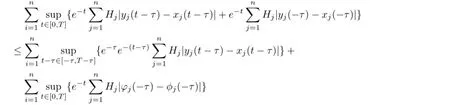
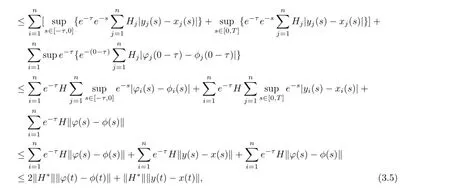
substituting(3.5)into(3.4)we can obtain which implies that

we can get

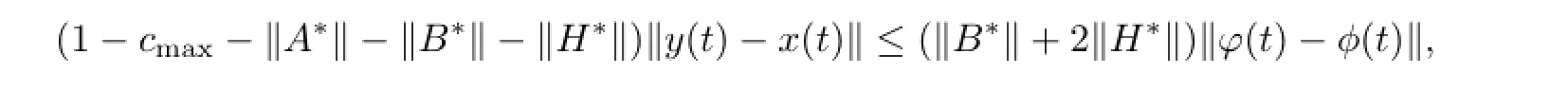
then

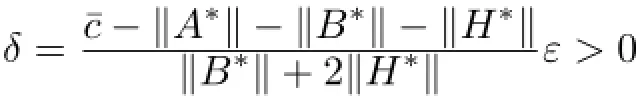
Then we get the main conclusion of this paper.

§4.Conclusion

In this paper,we mainly introduced a class of neutral fractional neural networks with delay. By introducing the defnition of norm and using the uniform stability,the sufcient condition for uniform stability of neutral fractional neural networks with delay is obtained.This is our main conclusion.Our future works include the uniqueness and uniform stability of its equilibrium point.

[References]

[1]PODLUBNY I.Fractional Diferential Equations[M].San Diego:Academic Press:1999.

[2]KAI DIETHELM,NEVILLE J FORD.Analysis of fractional diferential equations[J].J Math Anal Appl, 2002,265:229-248.

[3]ZHOU Yong.Basic Theory of Fractional Diferential Equations[M].Singapore:World Scientifc,2014.

[4]ZHOU Xian-feng,YANG Fu-li,JIANG Wei.Analytic study on linear neutral fractional diferential equations[J].Appl Math Comput,2015,257:295-307.

[5]AREFEH B,MOHAMMAD B.Fractional-Order Hopfeld Neural Networks[M].Springer:Lecture Notes in Computer Science,2009.

[6]ANASTASSIOU G.Fractional neural network approximation[J].Comput Math Appl,2012,64(6):1655-1676.

[7]BAO Hai-bo,CAO Jin-de.Projective synchronization of fractional-order memristor-based neural networks[J].Neural Networks,2015,63:1-9.

[8]WANG Hu,YU Yong-guang,WEN Guo-guang.Stability analysis of fractional-order Hopfeld neural networks with time delays[J].Neural Networks,2014,55:98-109.

[9]CHEN Li-ping,CHAI Yi,WU Ran-chao,et al.Dynamic analysis of a class of fractional-order neural networks with delay[J].Neurocomputing,2013,111:190-194.

[10]WANG Ding,LIU De-rong,LI Hong-liang,et al.Neural-network-based robust optimal control design for a class of uncertain nonlinear systems via adaptive dynamic programming[J].Inform Sciences,2014,282:167-179.

[11]JIANG Wei.Variation formulae for time varying singular fractional delay diferential systems[J].Fractional Diferential Equations,2011,1(1):105-115.

[12]JIANG Wei.The constant variation formulae for singular fractional diferential systems with delay[J]. Computers and Mathematics with Applications,2010,59(3):1184-1190

[13]LIU Pin-lin.Improved delay-dependent stability of neutral type neural networks with distributed delays[J]. ISA Transactions,2013,52(6):717-724.

[14]CAI Wei-ming,ZHU Song-ming,HE Hui-nong,et al.Research on decoupling control in temperature and humidity control systems[J].Chin Quart J of Math,2012,27(1):79-89.

[15]SI Jia-fang,JIANG Wei.Sliding mode control for fractional diferential systems with state-delay[J].Chin Quart J of Math,2012,27(1):117-122.

O175

:A

1002–0462(2016)04–0422–08

Received date:2014-12-16

Foundation item:Supported by the National Natural Science Foundation of China(11371027,11601055); Supported by the Natural Science Foundation of Anhui Province(1408085QA06);Supported by the Chuzhou University Planning Project(2015GH29);Supported by the Natural Science Research Project of Anhui Province(KJ2015B02)

Biographies:LI Yan(1990-),female,native of Chuzhou,Anhui,a teacher of Chuzhou University,M.S.D., engages in functional diferential equations;JIANG Wei(1957-),male,native of Hefei,Anhui,a professor of Anhui University,Ph.D.,engages in functional diferential equations;HU Bei-bei(1986-),male,native of Chuzhou, Anhui,a teacher of Chuzhou University,M.S.D.,engages in diferential diference equations.

2000 MR Subject Classifcation:34K37