Expression for the Group Inverse of the 2×2 Block Matrix

(Department of Mathematics,Southeast University,Nanjing211102,China;School of Mathematical and Physical Sciences,Xuzhou Institute of Technology,Xuzhou221006,China)

Expression for the Group Inverse of the 2×2 Block Matrix

DU Fa-peng

(Department of Mathematics,Southeast University,Nanjing211102,China;School of Mathematical and Physical Sciences,Xuzhou Institute of Technology,Xuzhou221006,China)

generalized inverse;group inverse;block matrix

§1.Introduction

Let C be a matrix algebra on complex feldBwith unitI.For a matrixA∈C,if there is a matrixB∈C such thatABA=A,BAB=B,thenBis called a generalized inverse ofA, denoted byA+.The matrixBis called the Drazin inverse ofA,ifBsatisfed

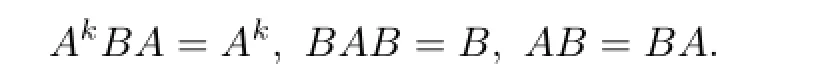
Bis denoted byAD.The least integerkis called the index ofA,denoted by ind(A).The idempotent matrixI-AADis denoted byAπ.If ind(A)=1,then we callBthe group inverse ofA,denoted byA#.In this caseAπ=I-AA#.

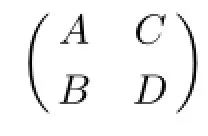
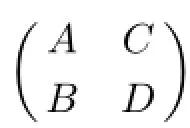
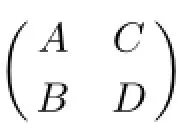
§2.Preliminaries

In this section,we give some important lemmas.

Lemma 2.1[25,30]LetA∈C.Then the following conditions are equivalent

(1)A#exists;

(2)AA++A+A-Iis invertible in C for someA+;

(3)A2A++I-AA+is invertible in C for someA+;

(4)A2A++I-AA+is invertible in C for anyA+;

(5)A+I-AA+is invertible in C for someA+;

(6)A+I-AA+is invertible in C for anyA+.

Lemma 2.2[23]LetA,B∈C andPbe a nonzero idempotent matrix in C.PutX=PAP+PB(I-P).

(1)IfPAPis group invertible and(PAP)(PAP)#B(I-P)=PB(I-P),thenXis group invertible too andX#=(PAP)#+[(PAP)#]2PB(I-P).

(2)IfXis group invertible,then so is thePAPand(PAP)(PAP)#B(I-P)=PB(I-P).

The following proposition comes from[25].Here,we give another proof.

Lemma 2.3[25]LetA∈C such thatA#exists.Then

ProofLetW=A2A++1-AA+,thenWis invertible by Lemma 2.1 sinceA#exists. SetP=AA+,Y=PW.It is easy to check thatY#exists andY#=W-1P.Note that

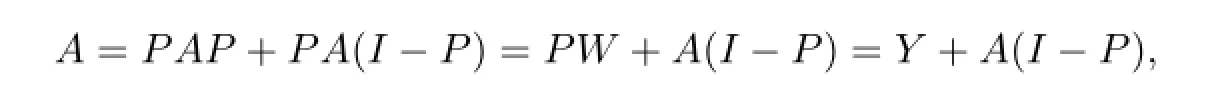
Y Y#A(I-P)=A(I-P)andAA+W=WAA+=A2A+.Thus,by Lemma 2.2,we have

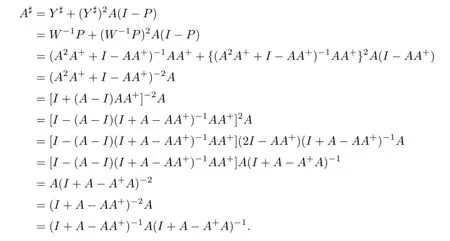
Proposition 2.4LetA∈C andTbe an idempotent matrix such thatTA=A.IfI+AT-Tis invertible,thenA#exists and

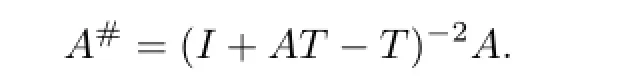
ProofPutW=I+AT-T;B=W-2A.Noting thatTW=WT=AT,we have

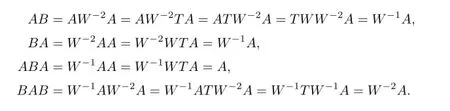
This indicateBis the group inverse ofA.

Proposition 2.5LetA,P,Q∈C withP,Qare invertible.LetB=PAQ.ThenB#exists ifAQP+I-AA+is invertible and

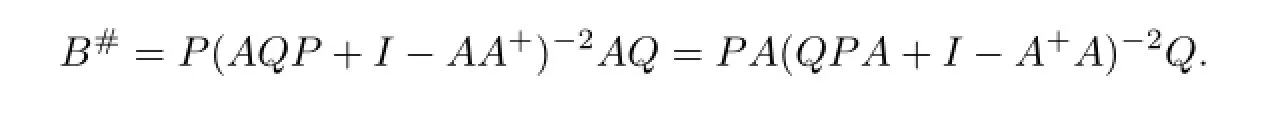
ProofNoting thatB+=Q-1A+P-1,we have

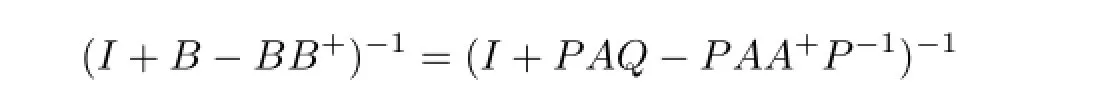
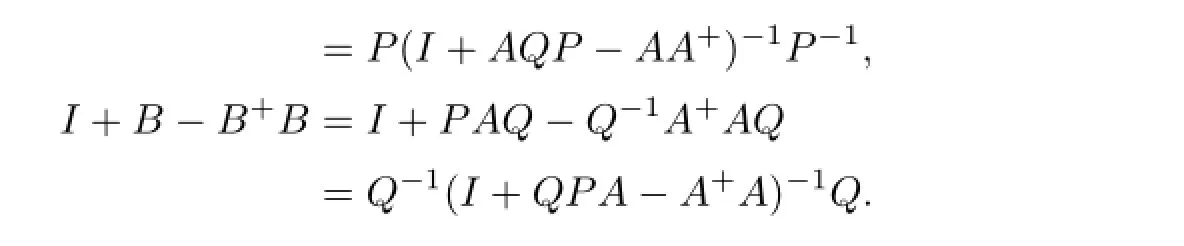
Thus,the assertion follows from Lemma 2.3.

LetX,Y∈C.For convenience,we setEX=I-XX+,FX=I-X+X.The following lemmas play an important role in the context which come from[25].

Lemma 2.6[25]LetX,Y∈C andU=EXY,Z=I+X+Y,S=X+XZFU.Then (X+Y)#exists ifX+Y+FUFSis invertible.In this case,

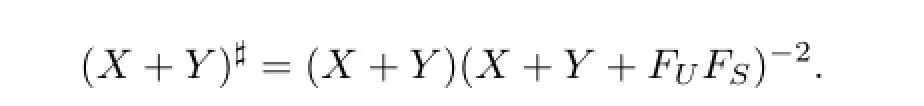
Lemma 2.7[25]LetX,Y∈C andV=Y FX,Z=I+Y X+,S=EVZXX+.Then (X+Y)#exists ifX+Y+ESEVis invertible.In this case,

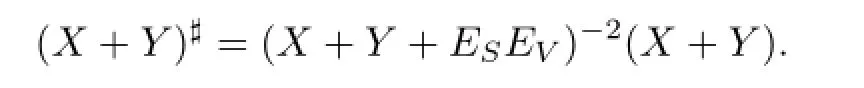
In[3,Theorem 2.1],J Ben´ıtez,X J Liu and T P Zhu consider(X+Y)#whenX#,Y#exist andXY=0.Now,we give a simpler proof in virtue of Lemma 2.6.

Corollary 2.8[3,Theorem2.1]LetX,Y∈C withX#,Y#exist.IfXY=0,then (X+Y)#exists and

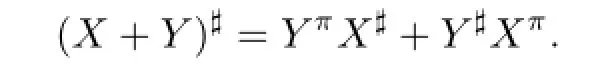
ProofSinceX#,Y#exist andXY=0,we haveX#Y=XY#=X#Y#=0 andXYπ=X,XπYπ=Yπ-XX#.Thus,U=Y,Z=I,S=XX#andFU=Yπ,FS=Xπ.

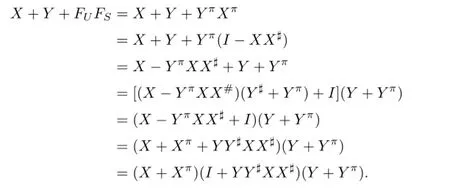
Noting that(I+Y Y#XX#)-1=I-Y Y#XX#,we have

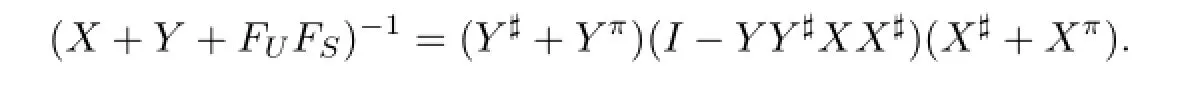
By Lemma 2.6,we have

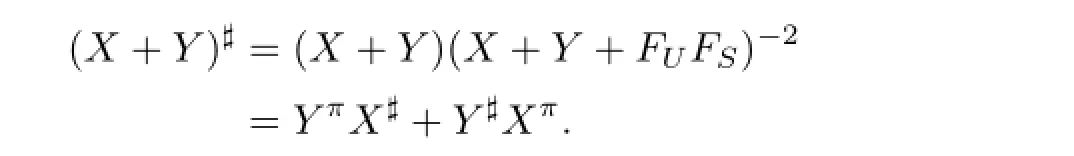
§3.Expression for the Group Inverse of 2×2 Block Matrix

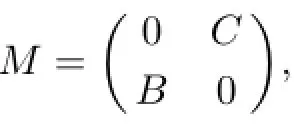
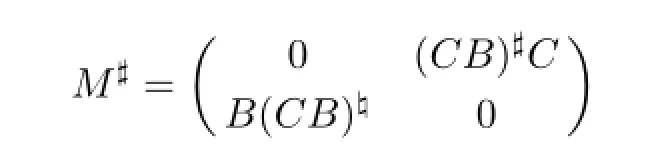
has been obtained in[16,Theorem 2.2]and[22,Lemma 2.2]under some conditions,respectively. But there remain another problem need to be solved,that is,how to calculate(CB)#?In the following theorem,we get a better result.

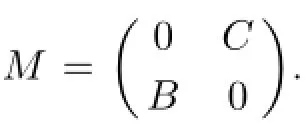
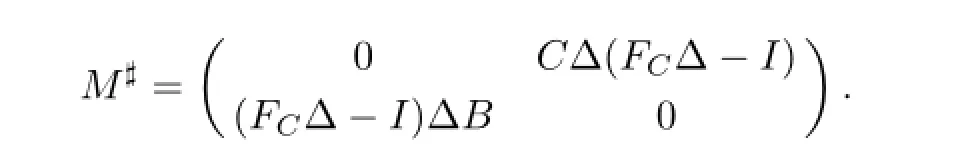
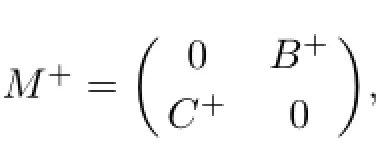
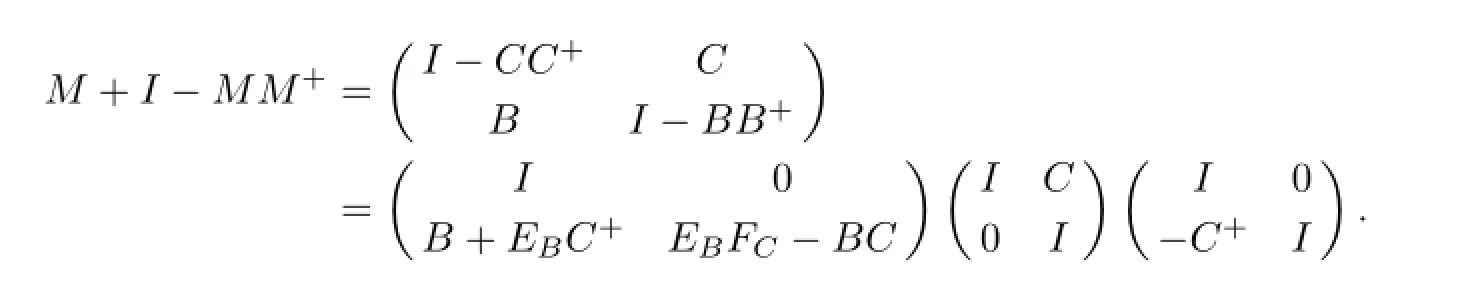
Thus,M#exists ifEBFC-BCis invertible by Lemma 2.1.

Put Δ=(EBFC-BC)-1.

Noting thatEBΔ-1=EBFC=Δ-1FC,ΔBCC+=-C+,B+BCΔ=-B+.We have ΔEB=FCΔ,FC=ΔEBFC,CΔEB=0,FCΔB=0,BCΔ=-BB+,ΔBC=-C+Cand

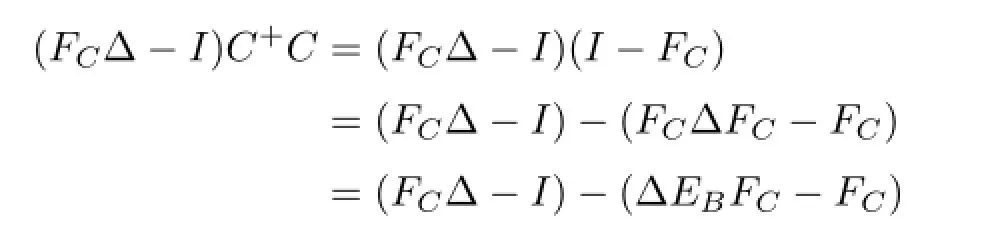
Thus,

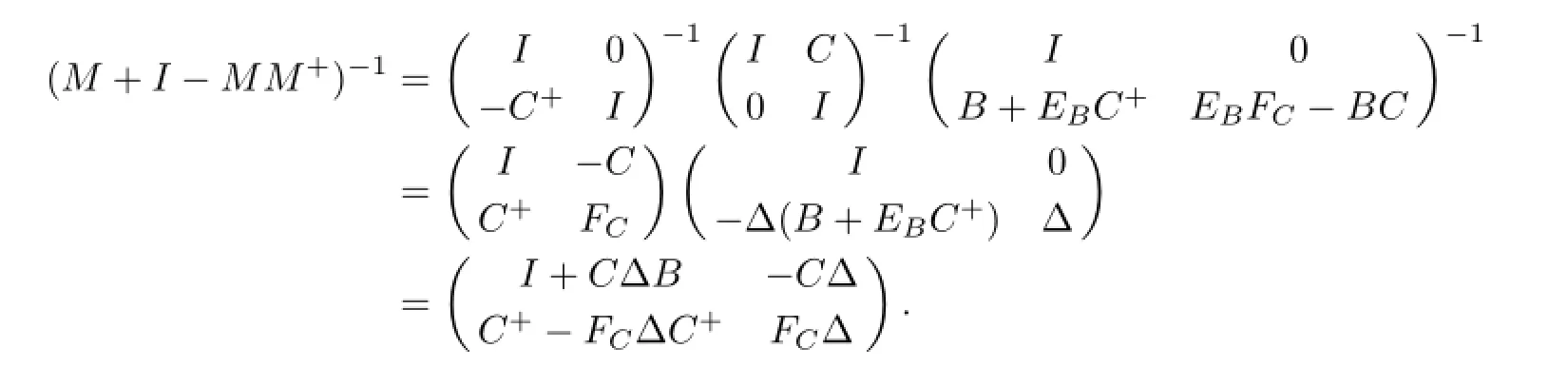
Thus,by Lemma 2.3,we have

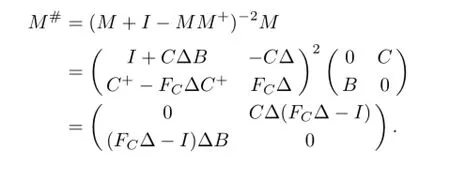
Using the result in Theorem 3.1,we give explicit expression of(CB)#and(BC)#.

Proposition 3.2LetB,C∈C.Then(CB)#,(BC)#exist ifEBFC-BCis invertible. Put(EBFC-BC)-1=Δ,then

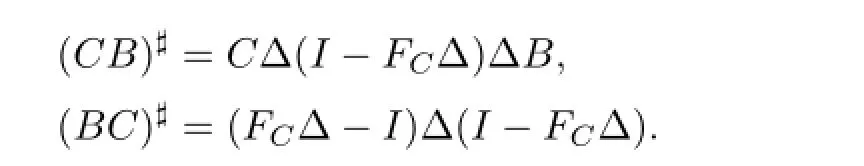
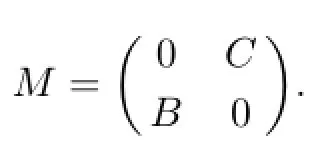
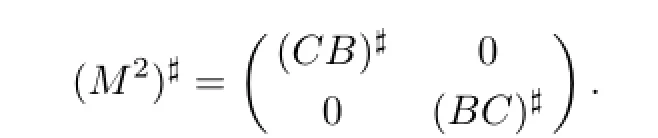
Using Theorem 3.1 and the equation(M2)#=(M#)2,we get

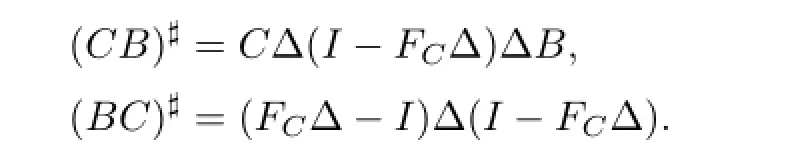
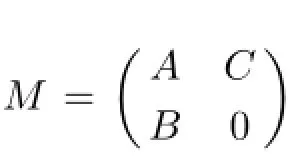
Here,Δ=(EBFC-BC)-1.

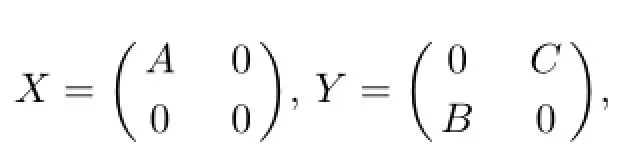
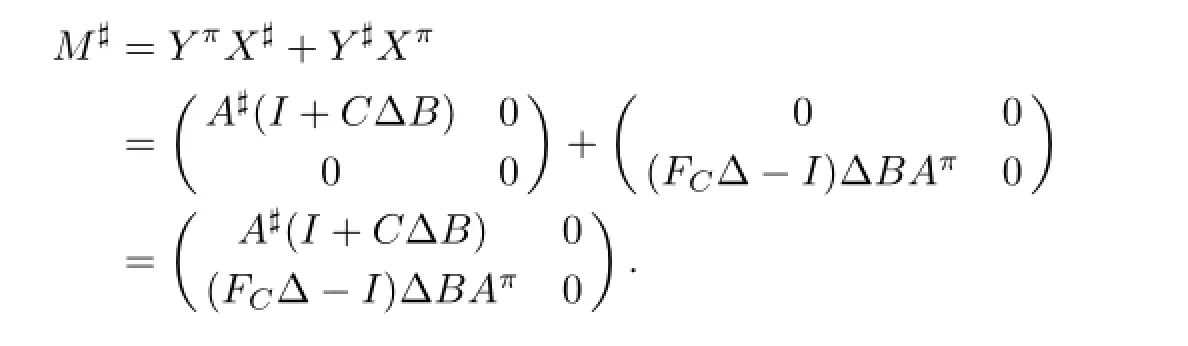
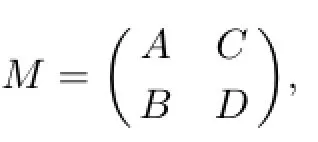
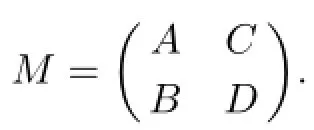
(1)(M+)11=A++(FAV+Z+A+C)(QBA+-(I-QZ)U+EA)-FAV+BA+;

(2)(M+)12=FAV+(I-ZQ)-A+CQ;

(3)(M+)21=(I-QZ)U+EA-QBA+;

(4)(M+)22=Q=FUS+EV.

From[27],we have

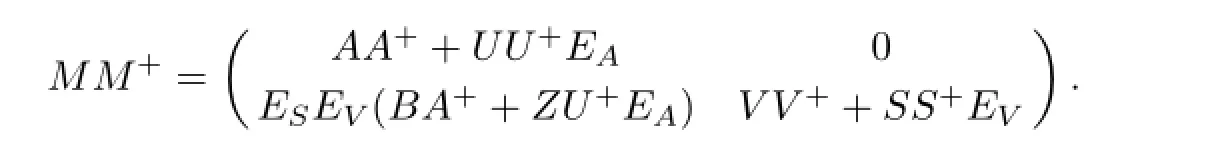
So,

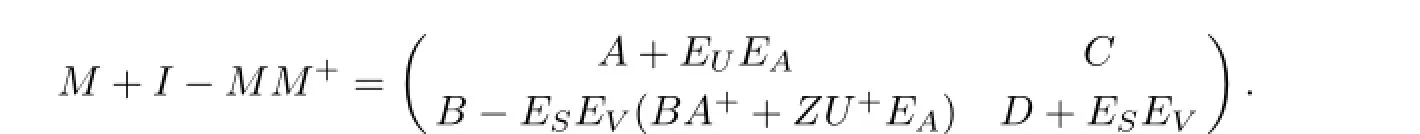
Thus,by Lemma 2.1,M#exists ifthe matrixM+I-MM+is invertible andM#=(M+IMM+)-2Mby Lemma 2.3.

Noting that the expression ofM#is very complicated and the calculation is routine,we only discuss the necessary and sufcient conditions such thatM#exists for some special cases in the following.

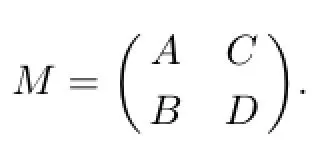
(1)IfA#exists andU=AπC=0,then

Hence,M#exists if

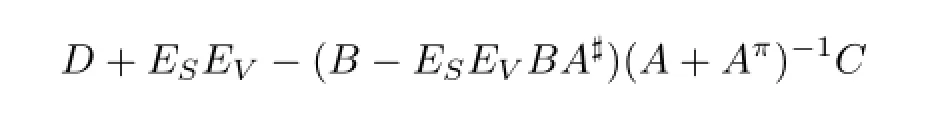
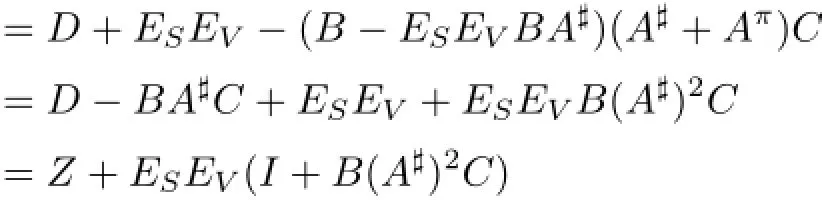
is invertible.

(2)IfAis invertible,thenU=0=V,S=Zand

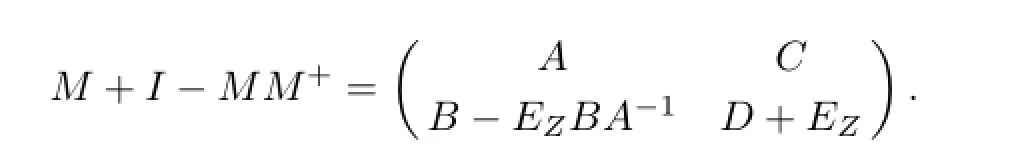
Hence,M#exists if

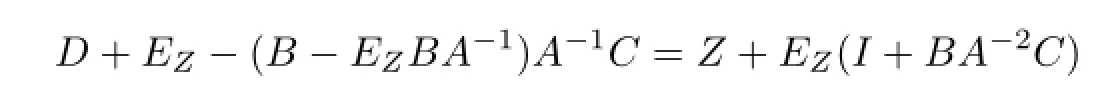
is invertible.

In addition,ifZ=0,thenM#exists ifI+BA-2Cis invertible.This is the result of Robert in[29].

(3)IfCis invertible,then

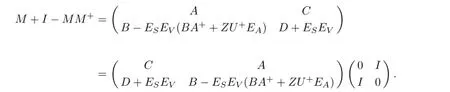
Thus,M#exists if

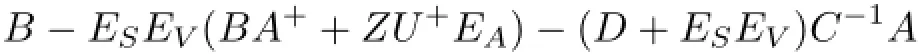
is invertible.

[1]BU Chang-jiang,ZHANG Kui-ze,ZHAO Jie-mei.Some results on the group inverse of the block matrix with a sub-block of linear combination or product combination of matrices over skew felds[J].Linear and Multilinear Algebra,2010,58(8):957-966.

[2]BU Chang-jiang,LI Min,ZHANG Kui-ze,et al,Group inverse for the block matrices with an invertible subblock[J].Appl Math Comput,2009,215:132-139.

[3]BEN´ITEZ J,LIU Xiao-ji,ZHU Tong-ping.Additive results for the group inverse in an algebra with applications to block operators[J].Linear Multilinear Algebra,2011,59:279-289.

[4]CAMPBELL S L,MEYER C D.Generalized Inverses of Linear Transformations[M].New York:Dover, 1991.

[5]CAMPBELL S L.Singular Systems of Diferential Equations I[M].London:Pitman,1980.

[6]CAMPBELL S L.Singular Systems of Diferential Equations II[M].London:Pitman,1982.

[7]CAMPBELL S L.The Drazin inverse and systems of second order linear diferential equations[J].Linear and Multilinear Algebra,1983,14:195-198.

[8]CAO Chong-guang.Some result of group inverse of partitioned matrix on body[J].J Nat Sci Hei-longjiang Univ,2001,18(3):5-7.

[9]CAO Chong-guang,TANG Xiao-min.Representations of the group inverse of some 2×2 block matrices[J]. International Mathematical Forum,2006,31:1511-1517.

[10]CASTRO-GONZALEZ N,DOPAZO E.Representations of the Drazin inverse for a class of block matrices[J]. Linear Algebra Appl,2005,400:253-269.

[11]CASTRO-GONZALEZ N,KOLITHA J J.New additive results for theg-Drazin inverse[J].Proc Roy Soc Edinburgh,2004,134A:1085-1097.

[12]CASTRO-GONZALEZ N,DOPAZO E,MARTNEZ-SERRANO M F.On the Drazin inverse of the sumof two operators and its application to operator matrices[J].J Math Anal Appl,2009,350:207-215.

[13]CASTRO-GONZALEZ N,MARTLNEZ-SERRANO M F.Drazin inverse of partitioned matrices in terms of Banachiewicz-Schur forms[J].Linear Algebra Appl,2010,432:1691-1702.

[14]CASTRO-GONZALEZ N,ROBLES J,VELEZ-CERRADA J Y.The group inverse of 2×2 matrices over a ring[J].Linear Algebra Appl,2013,438:3600-3609.

[15]CATRAL M,OLESKY D D,VAB DEN DREIESSCHE P.Block representations of the Drazin inverse of a bipartite matrix[J].Electron J Linear Algebra 2009,18:98-107.

[16]CATRAL M,OLESKY D D,VAN DEN DRIESSCHE P.Group inverse of matrices with path graphs[J]. Electron.J Linear Algebra,2008,17:219-233.

[17]CHEN Xu-zhou,HARTWIG R E.The group inverse of a triangular matrix[J].Linear Algebra Appl,1996, 238:97-108.

[18]CVETKOVIC-ILIC D S.A note on the representation for the Drazin inverse of 2×2 block matrices[J]. Linear Algebra Appl,2008,220:242-248.

[19]CVETKOVIC-ILIC D S,DJORDIJEVIC D S,WEI Yi-min.Additive results for the generalized Drazin inverse in a Banach algebra[J].Linear Algebra Appl,2006,418:53-61.

[20]DENG Chun-yuan,WEI Yi-min.A note on the Drazin inverse of an anti-triangular matrix[J].Linear Algebra Appl,2009,431:1910-1922.

[21]DENG Chun-yuan.A note on the Drazin inverses with Banachiewicz-Schur forms[J].Appl Math Comput, 2009,213:230-234.

[22]DENG Chun-yuan.Characterizations and representations of the group inverse involving idempotents[J]. Linear Algebra Appl,2011,434:1067-1079.

[23]DU Fa-peng,XUE Yi-feng.The perturbation of the group inverse under the stable perturbation in a unital ring[J].Filomat,2013,27(1):65-74.

[24]DU Fa-peng,XUE Yi-feng.Unifed approach to the expression for the Moore-Penrose inverse ofa-xy∗[J]. Chin Quart J of Math,2014,29(3):465-474.

[25]DU Fa-peng,XUE Yi-feng.The expression for the group inverse of the anti–triangular block matrix[J]. Filomat,2014,28(6):1103-1112.

[26]DJORDJEVIC D S,WEI Yi-min.Additive results for the generalized Drazin inverse[J].J Aust Math Soc, 2002,73:115-125.

[27]HARTWIG R E.Block generalized inverses[J].Arch Ratio Mech Anal,1976,61(3):197-251.

[28]MEYER C D.The role of the group generalized inverse in the theory of fnite Markov chains[J].SIAM Rev, 1975,17:443-464.

[29]ROBERT P.On the group inverse of a linear transformation[J].J Math Anal Appl,1968,22:658-669.

[30]XUE Yi-feng.Stable Perturbations of Operators and Related Topics[M].New Jersey:World Scientifc,2012.

[31]ZHAO Jie-mei,BU Chang-jiang.Group inverse for the block matrix with two identical subblocks over skew felds[J].Electron J Linear Algebra,2010,23:63-75.

O151.21

:A

1002–0462(2016)04–0412–10

Received date:2014-11-30

Foundation item:Supported by the Fund for Postdoctoral of China(2015M581688);Supported by the National Natural Science Foundation of China(11371089);Supported by the Specialized Research Fund for the Doctoral Program of Higher Education(20120092110020);Supported by the Natural Science Foundation of Jiangsu Province(BK20141327);Supported by the Foundation of Xuzhou Institute of Technology(XKY2014207)

Biography:DU Fa-peng(1974-),male,native of Xuzhou,Jiangsu,an associate professor of Xuzhou Institute of Technology,Ph.D.,engages in functional analysis application and operator algebra.

2000 MR Subject Classifcation:15A09,65F20