致密砂岩气藏压裂井两相流流入动态研究

2016-02-05崔永兴王明华

天然气勘探与开发 2016年4期

宋力覃勇崔永兴王明华王平

1.中国石油川庆钻探工程有限公司钻采工程技术研究院2.中国石油川庆钻探工程有限公司钻井液技术服务公司公司3.中国石油塔里木油田分公司塔中勘探开发项目经理部4.中国石油川庆钻探工程有限公司川西钻探公司

致密砂岩气藏压裂井两相流流入动态研究

宋力1覃勇2崔永兴3王明华4王平4

由于裂缝的影响，致密砂岩气藏压裂井易产水，准确地预测地层内流入动态对合理配产非常重要。针对致密砂岩气藏气水同产压裂井的渗流特征，将渗流场划分为地层及裂缝两个部分，以非达西稳态渗流理论为基础，基于扰动椭圆及等价发展矩形思想，分别建立了启动压力梯度及应力敏感的气水两相拟压力函数，推导出各区相应的产能方程，最终采用Newton-Raphson数值方法对产能方程进行求解。实例计算表明，该方程计算的气井无阻流量与实际产能测试结果误差较小，具有较强的实用性。

致密砂岩气藏压裂井产水井流入动态启动压力梯度应力敏感产能方程

致密砂岩气是现今开发规模最大的非常规天然气类型，是接替常规能源、维系我国能源安全的重要组成部分。由于致密砂岩气藏具有非达西渗流特征［1］，单井自然产量低，在实际生产中需通过压裂工艺获得工业产能。随着气井生产的进行，地层压力的下降易导致气藏周围连通关系较好的边、底水沿压裂裂缝侵入井底，压裂井产水改变了地层内气体的渗流特征，使气井产能进一步降低，流入动态随之发生变化。然而目前对于致密砂岩气藏产水压裂井的研究并不完善，一些学者基于非达西稳态渗流理论，研究了低渗砂岩气藏气井单相产能[2-5]，但忽视了压裂及气水两相渗流的影响；部分学者通过定义气水两相拟压力函数推导出气井稳态产能模型[6-9]，但仅适用于普通直井；还有学者对压裂井产能进行了分析[10-14]，但忽视了裂缝与基质应力敏感程度不同这一事实。鉴于此，笔者在前人研究的基础上，基于稳态渗流理论及扰动椭圆思想，建立并求解了综合考虑裂缝及基质非达西效应、气水两相渗流的压裂井产能方程。

1 致密砂岩气藏压裂井气水两相产能方程推导及求解

1.1 物理模型

气井流入动态的理论基础是合理的产能方程，假设一口压裂直井位于供给半径为re、储层有效厚度为h的均质各向同性圆形低渗透气藏中央，井筒半径为rw，边界定压，压力为pe，井筒压力为pwf。为简化计算，作如下假设：①压裂裂缝为沿井眼对称分布的垂直裂缝；②裂缝为有限导流裂缝；③裂缝剖面呈高为储层有效厚度的矩形；④地层与裂缝内均为气水两相等温稳态渗流，相间不存在化学作用；⑤不考虑地层及裂缝壁面污染；⑥忽略重力及毛管力的影响。在三维空间中，压裂井渗流物理模型如图1所示。

图1 三维空间中压裂井渗流物理模型图

将垂直裂缝井生产时的渗流场划分为裂缝与地层两个部分，水平平面渗流场如图2所示。其中裂缝内的渗流为气水两相线性流，渗流场为1区；地层内的渗流为以气井为中心，以裂缝端点为焦点的气水两相椭圆流，渗流场为2区。对于低渗致密砂岩气藏而言，应力敏感、启动压力梯度及滑脱效应的存在导致其渗流呈现出非达西流动特征。实验研究表明，致密砂岩气藏基块渗透率越低，应力敏感程度越强；裂缝渗透率越高，应力敏感程度越强，且裂缝的应力敏感程度远大于基块[15]。当储层出现气水两相流动时，一方面水相减少了气相渗流通道，另一方面水相与致密砂岩矿物发生物理化学作用降低岩石抗压强度，使得应力敏感更为明显[16]。因此在1、2两区渗流场内均应考虑应力敏感的影响。致密砂岩储层孔喉狭窄，由于孔隙连通性差，水相将堵塞气体流动，产生启动压力梯度现象，增大了气体渗流的阻力；气体分子在孔壁处无吸附薄层，产生滑脱效应，降低了气体渗流的阻力。为了研究二者对气水两相渗流的综合影响，朱维耀分别建立了含水低渗气藏在可动水、不动水及束缚水影响下的气井产能预测公式[17]。本文模型假设地层与裂缝内均为气水两相等温稳态渗流，符合可动水模型即气水两相启动压力梯度影响远高于滑脱效应。由于裂缝内渗流速度较高，因此仅在2区渗流场内考虑气水两相启动压力梯度的影响。

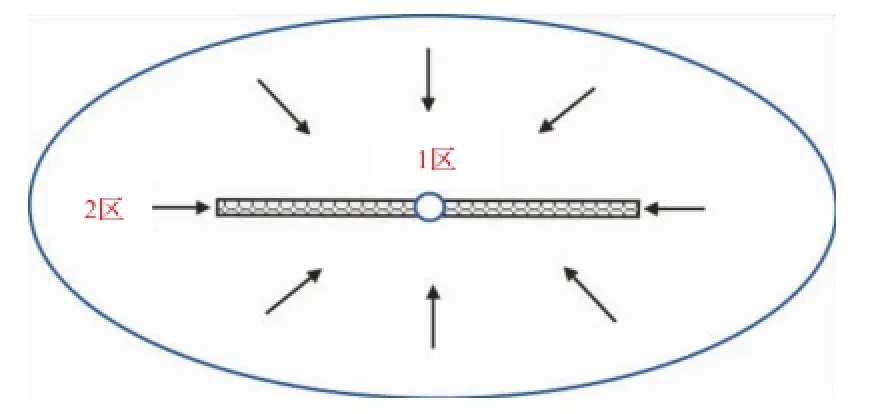
图2 压裂井水平平面渗流场示意图

1.2 产能方程推导

1.2.1 裂缝内产能方程推导

裂缝内的渗流场如图2中的1区所示。由于垂直裂缝内渗透率高，因此视气相在裂缝内的渗流为高速非达西流动，水相为达西流动。

气相渗流运动方程为：

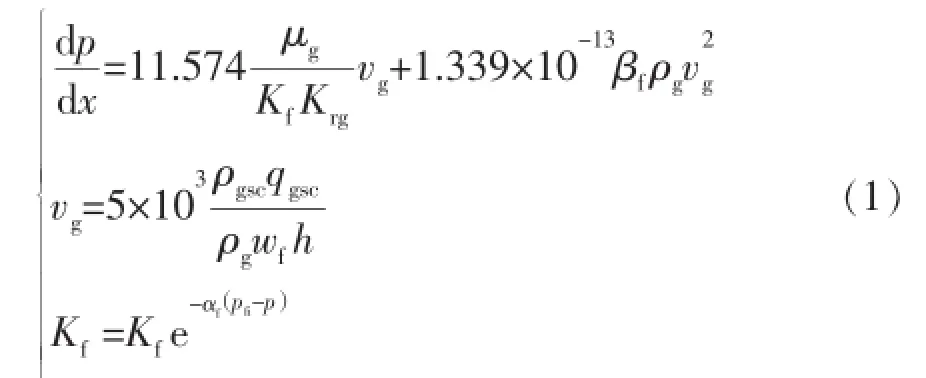
式中：

p—裂缝内的压力，MPa；

pf—初始裂缝尖端压力，MPa；

x—平面径向距离，m；

μg—气相黏度，mPa·s；

Kf—裂缝渗透率，mD；

Krg—气相相对渗透率，无量纲；

vg—气相在裂缝内的渗流速度，m/d；

βf—裂缝内的速度系数，m-1；

ρg—地下条件下的气相密度，g/cm3；

ρgsc—地面标准状况下的气相密度，g/cm3；

qgsc—标准状况下的气相体积流量，104m3/d；

wf—裂缝宽度，m；

h—储层有效厚度，m；

Kf—裂缝绝对渗透率，mD；

Kfi—裂缝原始渗透率，mD；

αf—裂缝的应力敏感系数，MPa-1。

水相渗流运动方程为

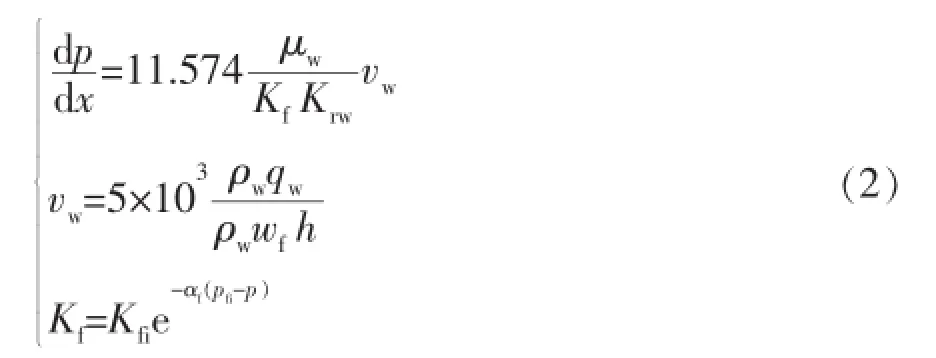
式中：

μw—水相黏度，mPa·s；

Krw—水相相对渗透率，无量纲；

vw—水相在裂缝内的渗流速度，m/d；

ρw—地下条件下的水相密度，g/cm3；

qw—地下条件下的水相体积流量，g/cm3。

将式（1）、式（2）分离变量相加，整理得：

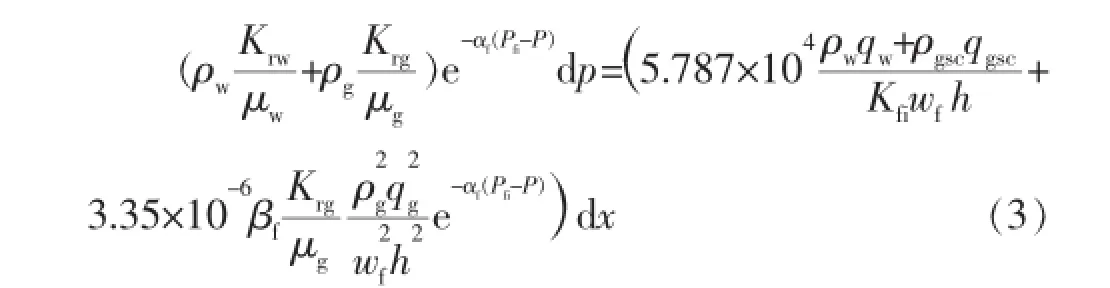
定义裂缝内气水两相拟压力函数为：

假设水气两相体积流量比为WGR，则水气两相总的质量流量为：

将式（4）、式（5）代入式（3），由井底到裂缝尖端积分，整理得：

式中：

pwf—为井底流压，MPa;

M（pf）—为裂缝尖端处的气水两相拟压力，（g·MPa）/（cm3· mPa·s）；

M（pwf）—井底处的气水两相拟压力，（g·MPa）/（cm3·mPa·s）；

xf—裂缝半长，m；

rw—井筒半径，m。

1.2.2 地层内产能方程推导

地层内的渗流场如图2中的2区所示。气井生产时，在垂直裂缝外的地层中将形成以气井为中心，以裂缝端点为焦点的气水两相椭圆渗流场[18]。该渗流场的共轭等压椭圆柱面及双曲流线簇如图3所示。

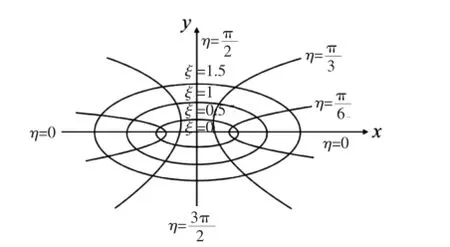
图3 地层内椭圆渗流场示意图

其中：

椭圆坐标与直角坐标的关系为：

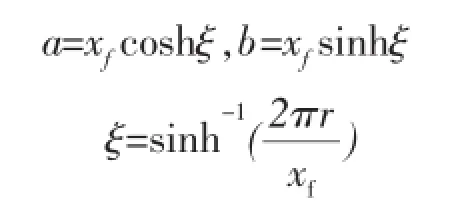
式中：

a—椭圆长半轴长，m；

b—椭圆短半轴长，m；

x、y—直角坐标，无量纲；

ξ、η—椭圆坐标，无量纲；

r—平面径向距离，m。

基于扰动椭圆概念，用发展的矩形描述等压椭圆簇，定义平均短半轴[14]为：

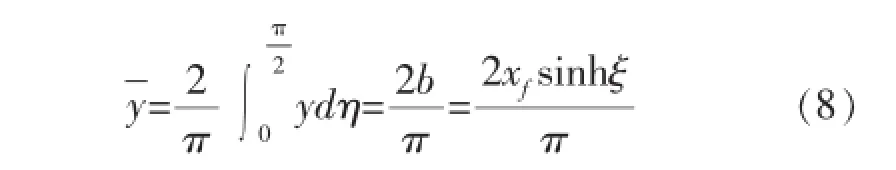
则

考虑启动压力梯度及应力敏感的气相渗流运动方程为：

式中：

λg—气相启动压力梯度，MPa/m；

K—储层绝对渗透率，mD；

Ki—地层原始渗透率，mD；

vg—气相在地层内的渗流速度，m/d；

pi—原始地层压力，MPa；

αf—地层基岩的应力敏感系数，MPa-1。

水相渗流运动方程为：

式中：

λw—水相启动压力梯度，MPa/m；

vw—水相在地层内的渗流速度，m/d。

将式(9)代入式(10)、式（11），分离变量相加，整理得：

定义地层内气水两相拟压力函数为

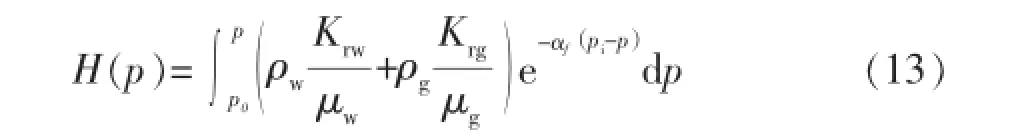
将式（5）、式（13）代入式（12），由裂缝尖端到定压边界积分，整理得：

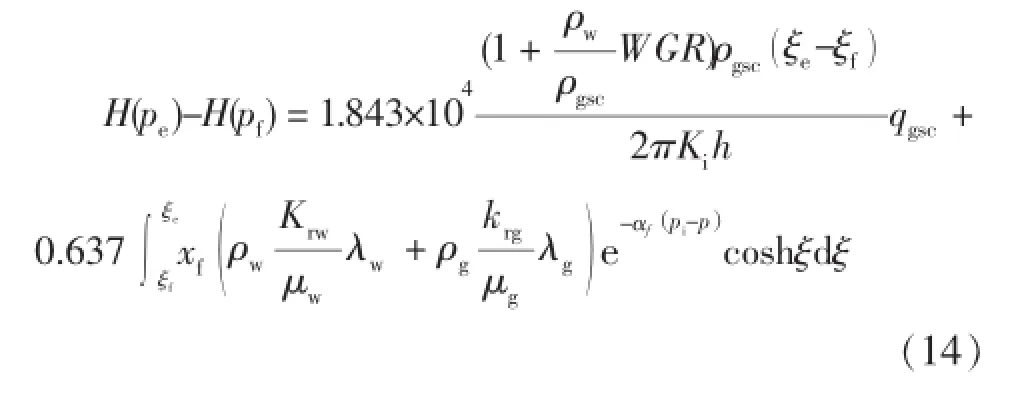
式中：

pe—气藏边界压力，MPa；

ξe—供给边界处的椭圆坐标，无量纲；

ξf—裂缝尖端处的椭圆坐标，无量纲；

H（pe）—气藏边界处的气水两相拟压力，（g·MPa）/（cm3· mPa·s）；

H（pf）—裂缝尖端处的气水两相拟压力，（g·MPa）/）cm3· mPa·s）。

1.3 产能方程求解方法

1.3.1 气水两相拟压力函数的求解

为了求解产能方程，首先应求解气水两相拟压力函数，其求解步骤为：

1）对于水相而言，ρw、μw随压力p变化较小，为简化计算视其为常数；对于气相而言，ρg、μg随压力变化明显，按Lee-Gonzalez-Eakin半经验法[19]将其表示为压力p的函数；

2）对于气水两相而言，首先根据相渗曲线分别确定Krw、Krg与Sw的函数关系；然后根据稳态渗流理论由式（5）可得：

由式（15）知，当水气体积流量比WGR一定时，根据步骤（1）可将Krw/Krg表示为压力p的函数；

3）由步骤（2）可得Sw与压力p的函数关系，再由Krw、Krg与Sw的函数关系即可求得任意压力p下的Krw、krg，将其代入式（4）及式（13）即可求得裂缝及地层内气水两相拟压力函数与压力的关系。

1.3.2 气水两相压裂井产能的求解

裂缝与地层内的两相拟压力函数表达式不同且裂缝尖端压力未知，因此需利用Newton-Raphson数值方法求解由式（6）及式（14）构成的非线性方程组中的裂缝尖端压力pf及气水两相压裂井产量qgsc。

用Newton-Raphson数值方法求解pf及qgsc的步骤为：

1）将式（6）及式（14）整理成等式右端为0的形式，记pf为x1，qgsc为x2，记式（6）为f1（x1，x2）=0，记式（14）为f2（x1，x2）=0；

2）在pf及qgsc的定义域范围内选取初值x1（0），x2（0）,给定允许误差ε＞0和最大迭代次数kmax；

3）对于k=0,1,…,kmax进行如下循环：

a.计算由式（6）及式（14）构成的非线性方程组的雅克比矩阵及F'（x（k））及F'（x（k））；

c.若||x（k+1）-x（k）||/x（k）＜ε，则x=x（k+1），计算结束，否则将x（k+1）作为x（k）进入步骤④计算；

d.当迭代次数k未超过kmax时继续上述运算，否则输出迭代失败，计算停止。

2 实例计算

苏里格致密砂岩气田内一口气水同产压裂直井X的基本数据为：原始地层压力为30.97 MPa，初始裂缝尖端压力与原始地层压力近似相等，地层温度为352.87 K，储层有效渗透率为0.4 mD，有效厚度为12.3 m，气井供给半径为714 m，井筒半径为0.1 m，裂缝半长为106.2 m，裂缝宽度为0.00 8 m，裂缝渗透率为50 D，气相启动压力梯度为0.00 4 MPa/m，水相启动压力梯度为0.008 MPa/m，地层基岩应力敏感指数为0.02/MPa，裂缝应力敏感指数为0.12/MPa，目前水气体积流量比为1 m3/104m3，气体平均偏差因子为0.910 3，气体相对密度为0.676 7，地层水密度为1.0 g/m3，地层水黏度为0.8 mPa·s。

通过编程计算分别求得地层及裂缝内气水两相拟压力函数随压力变化的关系曲线如图4所示，根据该图即可求得任意压力下的两区拟压力值。

图4 气水两相拟压力随压力变化的关系曲线图

气井X的产能系统试井基本数据如表1所示。利用本文建立的致密砂岩气藏气水压裂井产能方程及地层及裂缝内气水两相拟压力函数随压力变化的关系（图4），对表1中的数据进行处理，作如图5所示的产能分析曲线。经线性回归得到的气井X产能方程为：

表1 气井X产能试井基本数据统计表

图5 气井X产能试井分析曲线图

气井X通过修正等时试井获得的无阻流量为2.324×104m3/d，利用本文建立的低致密砂岩气藏气水两相压裂井产能方程求得无阻流量为2.214×104m3/d，两者绝对误差为0.11×104m3/d，相对误差为4.73%，绝对误差及相对误差均较小，说明本文建立的产能方程能较为合理地预测低渗致密砂岩气藏气水两相压裂井的产能。