基于统计学方法的卫星在轨热变形快速分析

张也弛，张龙，罗文波，潘腾

北京空间飞行器总体设计部，北京 100094

基于统计学方法的卫星在轨热变形快速分析

张也弛*，张龙，罗文波，潘腾

北京空间飞行器总体设计部，北京 100094

为使用在轨实测温度数据辅助完成成像载荷视轴指向的在轨标定，首次将应用于地统计学中的普通克里格法用于卫星在轨温度场的无偏估计，提出了一种基于统计学方法的在轨热变形快速分析方法。应用热试验过程中星上少量温度实测数据进行卫星温度场的无偏估计，并将温度计算结果赋值到有限元模型，进而完成了热变形分析。应用此种方法，相比通过热物理方法进行温度场分析，可将热变形分析的工期缩短数日，且载荷变形的分析结果与试验实测结果的误差在1′左右，可较准确地得到载荷视轴在热变形作用下的指向变化。文章可为卫星在轨热变形的快速分析提供参考。

温度实测点；快速热变形分析；统计方法；普通克里格法；变差函数；有限元；卫星

某些成像载荷与光学成像载荷不同，例如X射线望远镜，难以通过对天空或地面已知目标成像来进行自身指向的标定，而是始终依赖卫星平台提供的载荷光轴指向，利用载荷观测数据进行图像重建，最终确定X射线源的空间位置。因此，需要选择适当的方法进行载荷视轴指向的标定，进而保证载荷的点源定位精度。指向精度的偏差由多种因素引发，其中影响最大、也最难进行标定的就是在轨温度场变化引发的热变形。通常，温度场借助热物理方法进行分析[1-2]，为了得到载荷在轨由于热变形引起的实时指向变化，本文拟通过在轨温度遥测数据对热变形进行分析。

热变形分析首先需要温度场作为输入条件，但相比有限元分析所需的温度场数据，星上所能提供的在轨温度遥测点非常少，要依据在轨温度实测值进行热变形的计算，只能通过插值等方法对整个载荷的温度场数据进行估计。另外，由于温度场在有限元模型中的赋值需要很大的工作量，导致工期较长，文献[3]实现了有限元模型中温度场的自动批量导入，避免了手工赋值耗时过长的问题。然而，热变形分析过程中还有另一个工作量很大的环节，即分析需要有限元模型上所有节点的温度值作为输入条件，该温度场由热分析计算给出。在进行热分析前，在轨工况的选择需要对星内设备工作情况，外热流情况等多种因素进行统计，如果要提供卫星在大量不同时刻的温度分布情况，需耗费大量时间。文献[4]应用插值方法对卫星红外遥感器辐射定标光机系统的热变形进行了分析，证明了该系统热变形可满足光学准确度要求，可为结构快速热变形分析提供借鉴，但该系统体积规模较小，也决定了其温度分布并不十分复杂，所以该文未对所用插值方法及估计结果的准确性开展讨论。

地统计学中，对于大气温度测算等复杂问题通常借助一些已知测点来完成，即通过选取合适的无偏估计算法，完成对未知位置的温度估计，十分方便快捷。普通克里格法[5]作为一种无偏估计算法，在地统计学中已得到成熟应用[6]，在空间温度估计方面的应用也得到广泛研究[7]。由于普通克里格法得到学者和工程师的广泛肯定，对该算法的研究也不断深入[8-9]，并且依据空间特性的不同发展出了简单克里格法、协同克里格法等多种推广型算法[10-11]。

本文首次探讨了普通克里格法应用于卫星热变形分析的可行性，提出一种基于在轨温度遥测数据进行卫星热变形快速分析的方法，用以跳过繁琐的热分析工况选择过程。文章使用热平衡试验过程中卫星结构上的少量温度实测数据，利用普通克里格法进行卫星温度场估计，再进行温度场赋值与变形计算，最后将分析结果与热试验过程中的实测变形结果进行比较，说明这种结构热变形分析方法的正确性和可行性。

1 热变形快速分析方法

传统热变形分析采用热分析结果作为温度场输入，分析的工期往往需要数日乃至更长的时间，本文提出的方法与其最大的不同，在于本方法跳过热分析步骤，直接使用统计学理论，基于少量温度实测点完成结构的温度场分析，用于估计卫星在轨任一时刻的变形情况，为卫星在轨热变形分析提供一种快速有效的方法。

1.1 普通克里格法

普通克里格法依据温度实测点即可完成温度场估计，因此该方法可依据星上的温度遥测数据，提高热变形分析工作的效率，在航天任务中十分有利于在轨应用。该方法分为三步，如图1所示：1)根据已知测点数据，对空间场进行结构分析，选取并提出变差函数模型；2)通过优化算法(本文采用拉格朗日乘数法)求解克里格方差的极小值，若克里格方差满足要求，则进一步计算插值权值，若克里格方差不满足要求，则回到步骤1，重新选取变差函数；3)得到计算插值权值后，进行克里格插值计算。

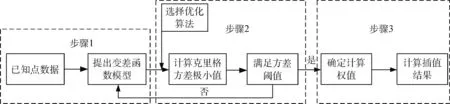
图1 普通克里格法计算示意Fig.1 Calculation process of ordinary Kriging

普通克里格法一般公式为

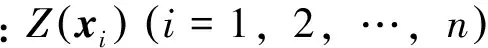
待定点值的期望误差应为0，即有

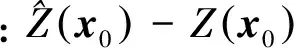
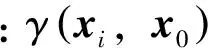
变差函数根据实验变差函数拟合得到，实验变差函数由采样点及其坐标计算，算式如下：

(5)

得到实验变差函数后，可用其拟合理论变差函数，拟合方法见文献[6]。对变差函数的拟合，已经有成熟的专用软件及Matlab工具箱，用于根据采样点及其坐标拟合变差函数。

在式(2)的约束条件下，通过优化方法求解式(4)中克里格方差的极小值，也就得到了相应变差函数模型下的权重λi，即可进一步开展未知点的温度计算。

进行二维估计时，对某个点进行数据估计可采用四分法，如图2所示：一般对平面某点进行估计时至少存在4个采样点，且应保证4个象限均有采样点存在(边界点除外)。进行三维数据估计时，宜采用八分法，即最好保证空间8个象限均有采样点存在。

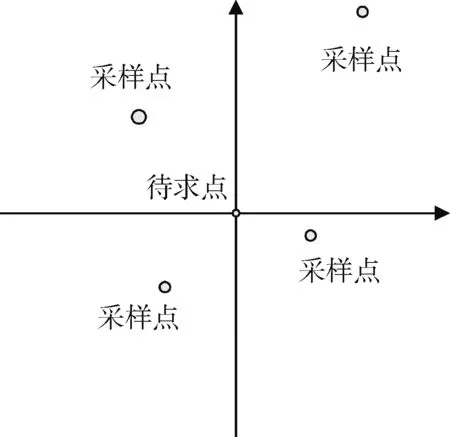
图2 采样点分布Fig.2 Sampling point distributions

对某个区域内进行温度场估计，就是根据邻近数据和变差函数进行数据平滑的过程。如果温度场存在分布不均匀甚至丛聚现象，且采样点数据较少，甚至在温度突变位置无采样数据，则会对估计结果造成较大偏差。因此在结构上存在热源，或者在隔热层的两侧存在温度突变的区域都应布置采样点。

1.2 应用普通克里格法的热变形快速分析

由以上方法替代传统热变形计算中的热分析步骤，完成温度场估计后，即可进行热变形计算，本文的热变形计算在Nastran中完成。Nastran在进行有限元计算时，所使用的bdf文件是Patran根据有限元模型及工况条件生成的，这其中就包含了热变形分析所需的温度场数据。要在Nastran中进行热变形分析，需要将在外部生成的温度场数据导入bdf文件。

本文使用统计学方法推算有限元模型上所有节点的温度值后，采用VC++编写接口文件，将计算得到的温度场写入bdf文件，实现有限元模型温度场的赋值，最后将热变形计算结果与热平衡试验中的实测变形结果进行比较，进而说明方法的正确性。整个热变形运算方法的流程如图3所示。

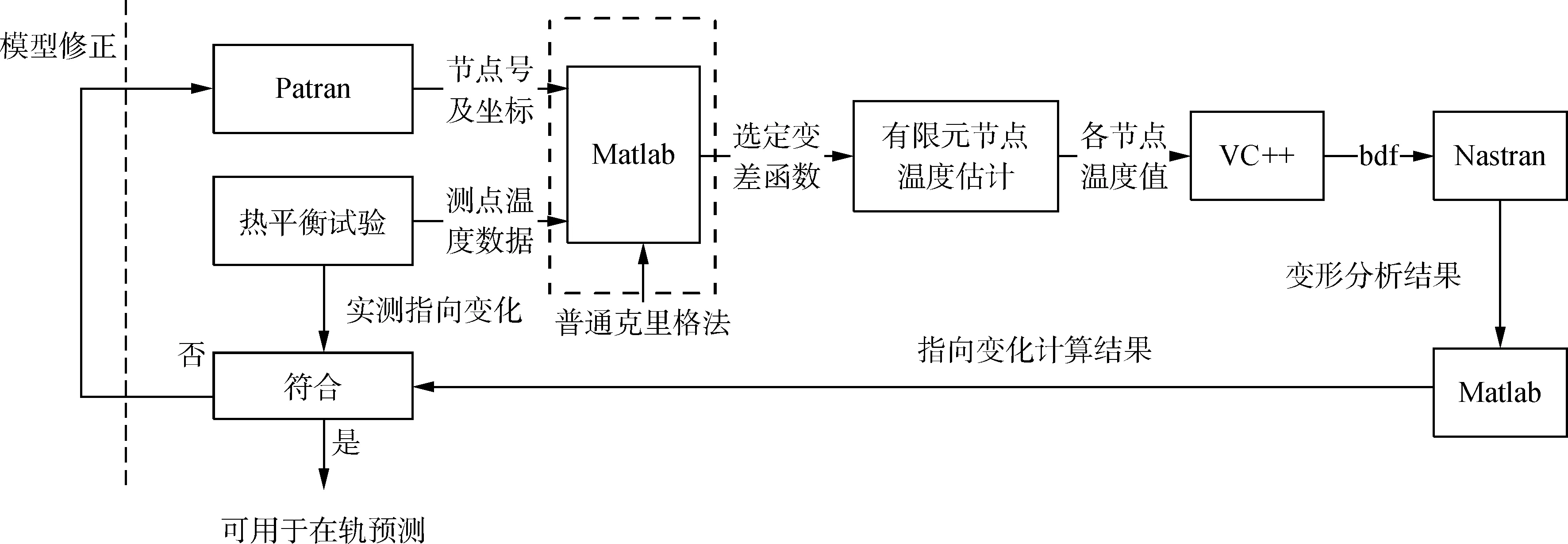
图3 快速热变形计算方法流程Fig.3 Process of the rapid thermal deformation analysis

2 分析结果和试验验证

2.1 结构形式

本文所分析的星上载荷，其主体结构由下板、中板、上板以及三层板间的支撑筒组成。其中支撑筒内部采用主动温控，上板采用散热涂层进行被动控制。在有限元分析中，对上板、中板和下板的建模采用了二维网格单元，对支撑筒的建模采用了二维网格和三维HEX8单元。上板、中板和下板采用二维数据估计；支撑筒形状较复杂，采用三维估计。

在诸多因素中，有限元模型对热变形的影响占据了很大的比重。本文所用星上载荷的有限元模型为经过多次试验修正的模型，包括正弦振动试验修正与热变形修正，这些修正对于最后分析精度的保证都起到了重要作用。

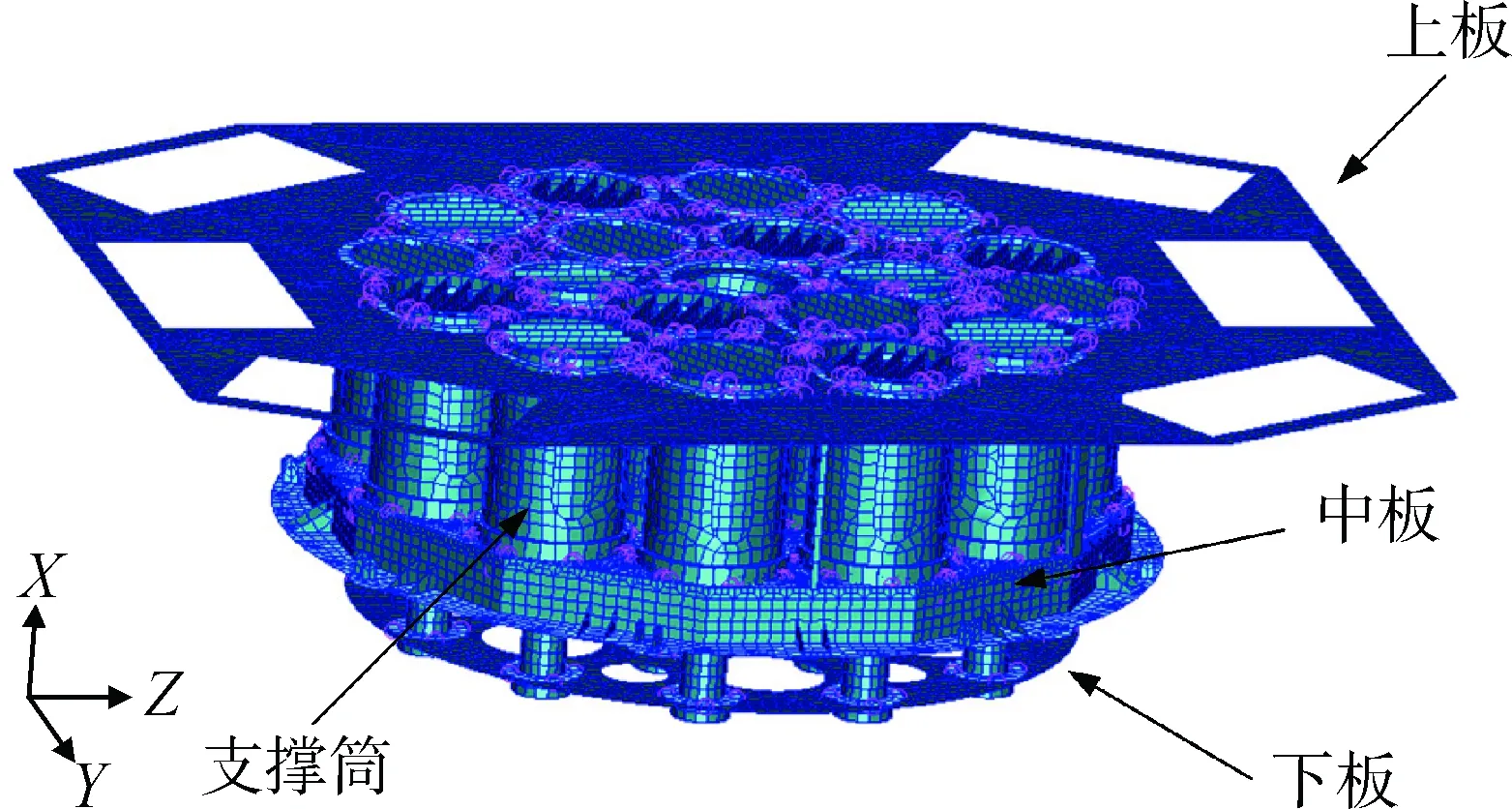
图4 结构形式示意Fig.4 General view of the structure

2.2 试验结果

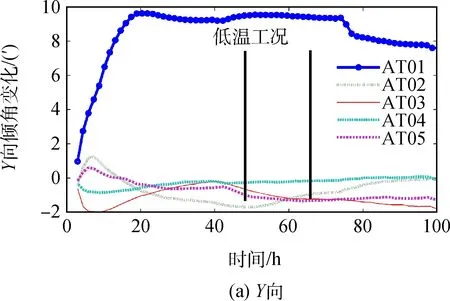
在该载荷热平衡试验过程中，星上安装了温度遥测点，这些测点温度即为普通克里格法进行温度场估计的输入条件；同时，为了解科学成像载荷在热变形作用下的视轴指向变化，在星上安装了倾角传感器。温度及倾角测点位置见图5～图6，CD1～CD26为温度测点，测点温度见表1。AT01～AT05为倾角传感器。5个倾角传感器(AT01～AT05)实测的Y、Z方向(水平方向)倾角变化结果见图7，图中第47～67 h为低温工况时段。所测位置最终倾角可由Y、Z方向倾角进行计算：

式中：α、β分别为Y、Z方向倾角测量值；γ为总倾角变化。

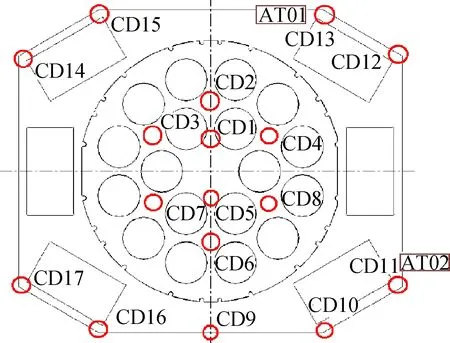
图5 上板温度及倾角测点示意Fig.5 Temperature and dip angle sensors on the upper plate

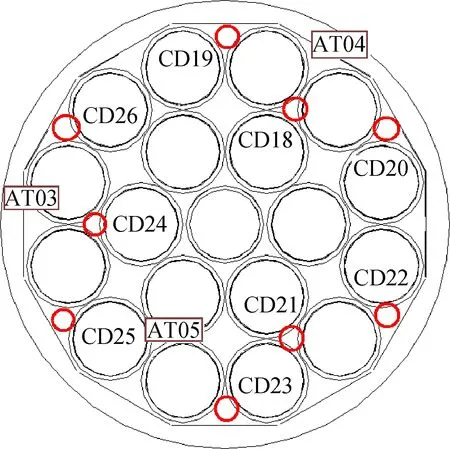
图6 中板温度及倾角测点示意Fig.6 Temperature and dip angle sensors on the middle plate

2.3 分析结果及讨论

根据已知点数据，需要建立变差函数模型来进行图1中后续步骤的计算。对于温度分布来说，距离测点较近的点，其温度值与测点温度值关联性更大；反之，距离测点较远的点，其温度值与测点温度值关联性则较小，根据这种特点，本文中的变差函数初步确定采用高斯型：

式中：θi为比例参数，该参数依据已知测点数据，由最大似然估计确定。根据实测温度数据拟合的变差函数见图8。

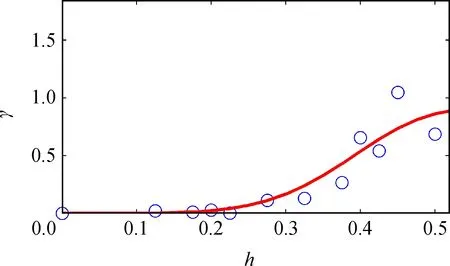
图8 根据采样点拟合的变差函数Fig.8 Variogram fitted by the sampling points

使用变差函数完成插值后，采用交叉验证法验证结果，即假设部分测点温度未知，用其他采样点对这些点进行估计，再与实测值进行比较。变差函数选取的越符合实际，那么克里格估值结果也就越符合实际结果。分别对CD1～CD4、CD5～CD8进行估计：在估计CD1～CD4温度时，采用CD5～CD17作为已知温度点；在估计CD5～CD8温度时，采用CD1～CD4、CD9～CD17作为已知温度点，将CD1～CD4、CD5～CD8实测温度和采用普通克里格法得到的温度值进行比对，结果见表2，可见估计值与实测值偏差很小，均在0.6℃以内。说明变差函数选用高斯型能够较准确地还原温度场，可以进行下一步计算。

使用所有试验实测数据进行估计，整个载荷上板的温度估计结果见图9。

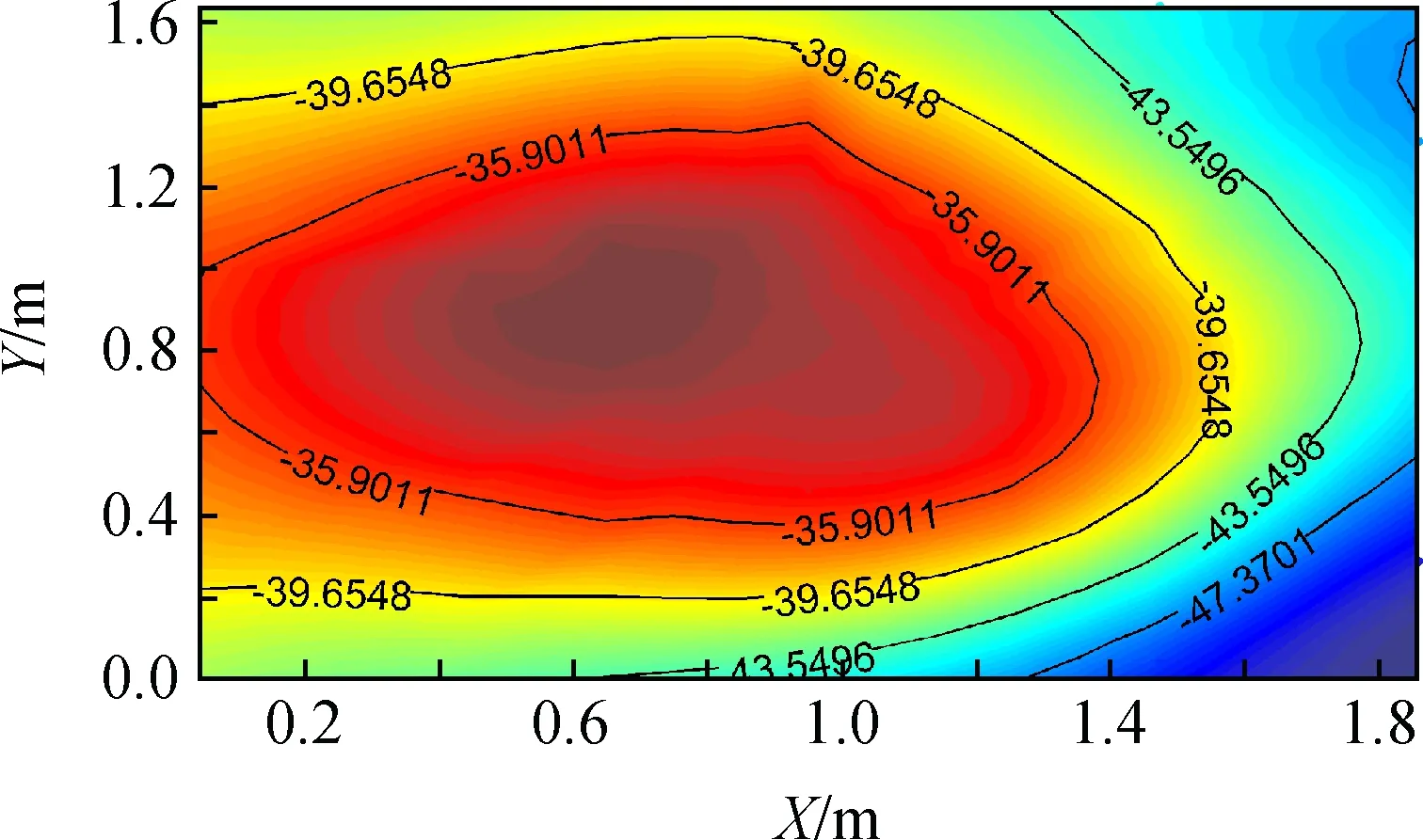
图9 上板温度估计结果Fig.9 Estimate results of temperature on the upper plate

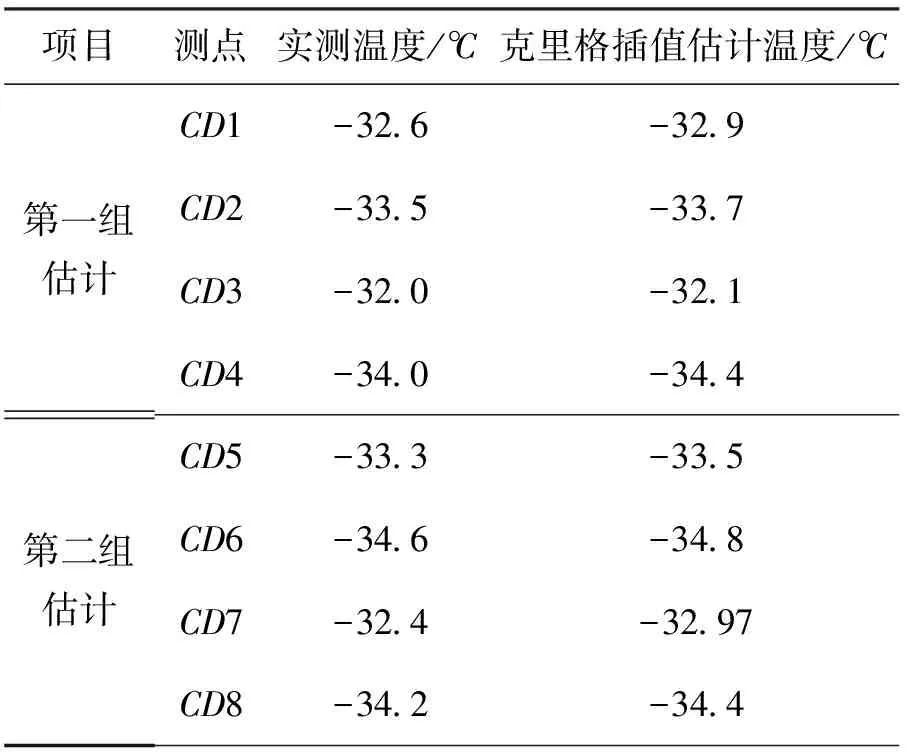
项目测点实测温度/℃克里格插值估计温度/℃第一组估计CD1-32 6-32 9CD2-33 5-33 7CD3-32 0-32 1CD4-34 0-34 4第二组估计CD5-33 3-33 5CD6-34 6-34 8CD7-32 4-32 97CD8-34 2-34 4

在温度稳定后，图4中载荷温度变化较大的结构为上板和中板。而对于板间的同一支撑筒来说，在温度稳定后，支撑筒上部与下部温差仅在1.5℃左右，无论采用克里格插值还是更简单的泰森多边形插值，对分析结果的影响仅反映在一阶小量。鉴于支撑筒的温度分布特点，在同一支撑筒上最多只布置了两个测点。以其中的一个支撑筒为例说明其三维温度场建模步骤，如图10所示：首先建立一个包络该支撑筒的简单有限元网格，将支撑筒顶部与底部测点温度分别赋值于该有限元网格的顶部节点和底部节点；之后使用Patran中自带的Field生成方法(这里采用泰森多边形法[12])生产空间场；最后使用该Field将温度场赋值给支撑筒。

载荷温度场最终映射结果见图11。

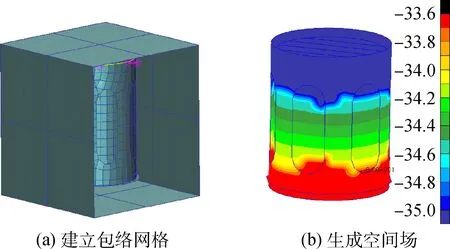
图10 支撑筒温度场赋值Fig.10 Temperature assignment of the supporting column

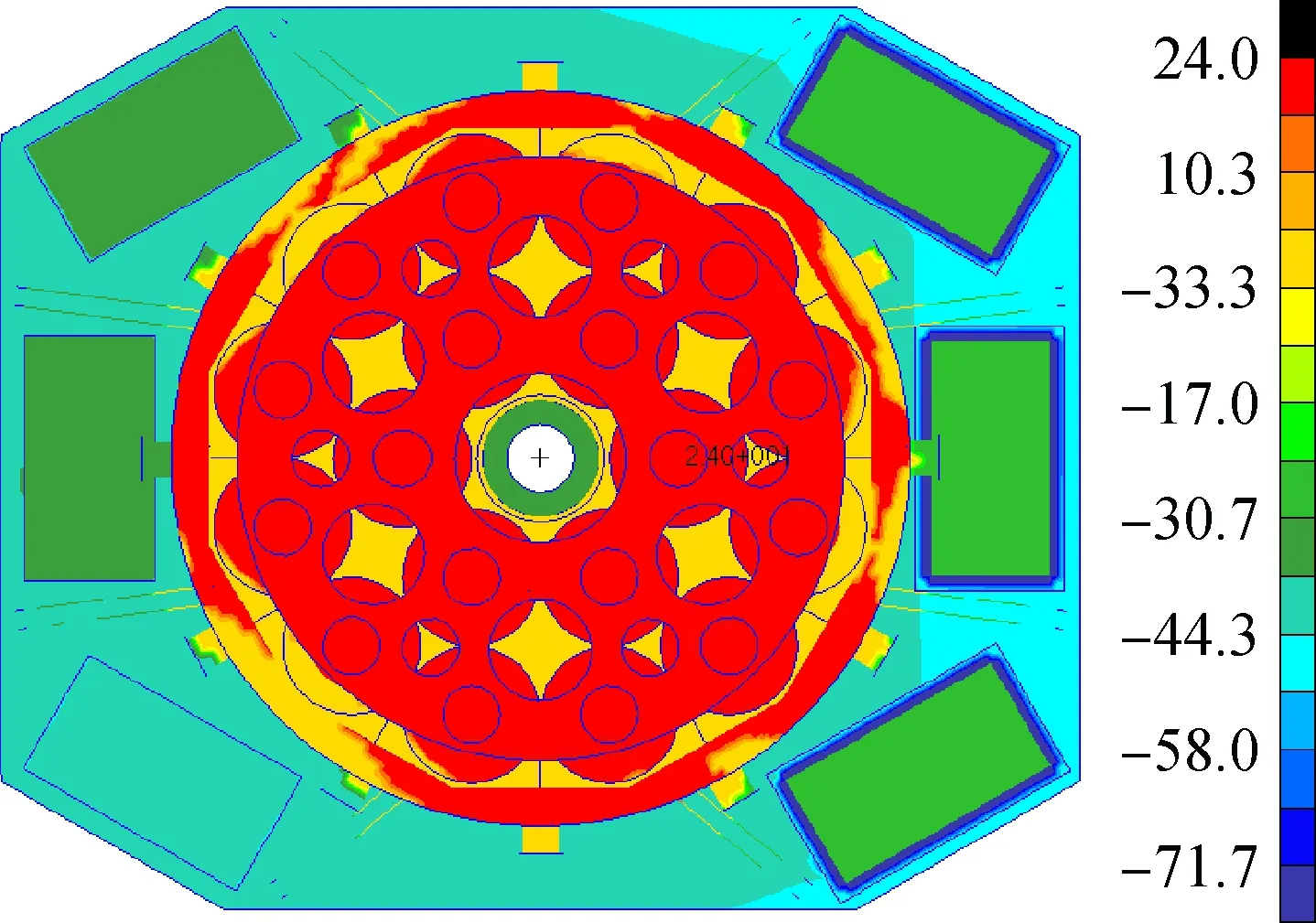
图11 温度场映射结果Fig.11 Mapping results of the temperature field

完成温度场映射后，即可使用Nastran进行有限元分析，上板变形见图12，可见变形结果为上板四周向上翘曲，距离中心基准越远处变形值越大。

利用变形分析结果，对图5～图6中的倾角传感器AT01～AT05所在位置进行热变形计算，分析得到的倾角变化与试验实测倾角变化的比较见表3。

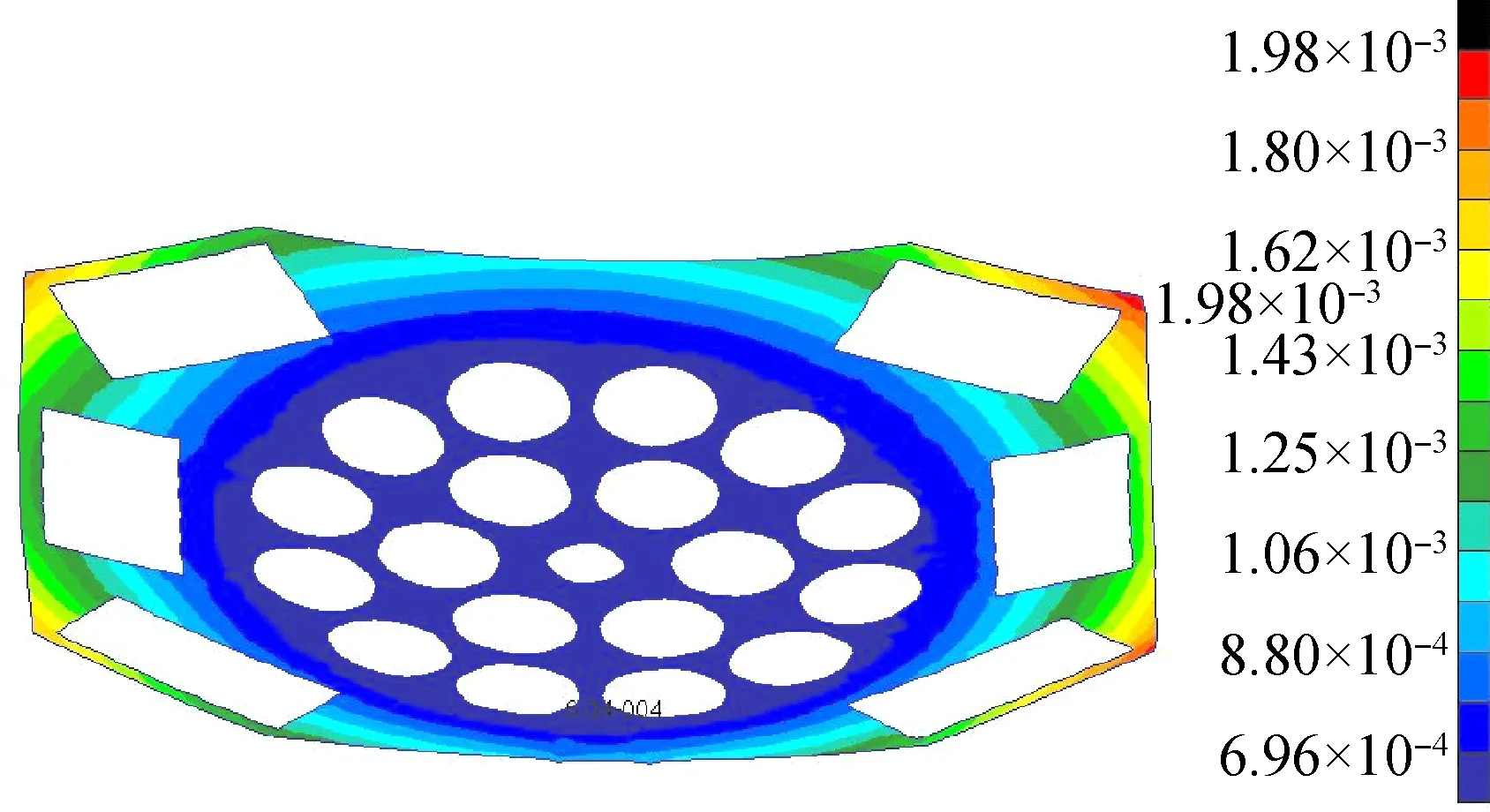
图12 载荷上板变形Fig.12 Thermal deformation of the upper plate of the payload

由表3中比较可见，AT01、AT03、AT05的分析值与实测值之差均在1′以内，AT02、AT04分析值与实测值之差在1′～2′之间，分析结果与试验结果吻合良好。对于科学成像载荷热变形的计算已经达到了较高的精度，可满足该载荷的要求，因此文中所用分析过程可应用于该载荷视轴在热变形作用下的指向变化估计。

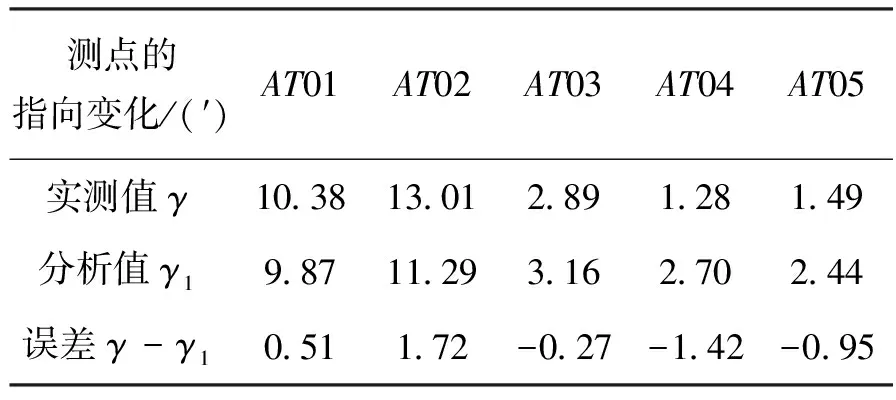
表3 倾角变化的试验值与分析值的比较

同时，本方法使用在轨温度遥测数据估计结构温度场，因此分析结果也对应着温度遥测数据采集时刻的变形情况。所以，需要知道在轨某一时刻的结构变形情况时，只需提供其附近时刻的温度遥测数据，就可对该时刻的变形情况进行分析。

3 结束语

文章首次应用一种统计学方法——普通克里格法，提出了卫星在轨热变形计算的快速方法。该方法省略了繁杂的热分析过程，将温度场估计工期由数天甚至数周减少为几小时，可用于卫星的实时在轨变形估计。基于上述方法，本文对卫星载荷热变形进行了分析，结果表明，分析值与实测值差别在1′左右，满足该载荷的指向精度要求。

基于本文的工作，可在后续研究中进一步探索如何应用变差函数的结构套合、层次套合及各向异性套合等方法，针对结构温度场分布更复杂的情况进行估计。达到快速性计算并预估复杂温度场和热变形的目的，最终以能实施温度或变形的主动控制为目标开展下一步工作。

References)

[1] 游思梁，陈桂林，王淦泉. 星载辐射计扫描镜太阳辐射热-结构建模与仿真[J].中国空间科学技术，2011，31(1)：62-69.

YOU S L，CHEN G L，WANG G Q. Thermal-structural modeling and simulation for scan mirror on imager in solar radiation[J].Chinese Space Science and Technology，2011，31(1)：62-69(in Chinese).

[2] 张镜洋，常海萍，王立国. 小卫星瞬态热分析模型修正方法[J]. 中国空间科学技术，2013，33(4)：24-30.

ZHANG J Y，CHANG H P，WANG L G. Correction method for transient thermal analysis model of small satellite[J]. Chinese Space Science and Technology，2013，33(4)：24-30(in Chinese).

[3] 张思斯. 扫描辐射计及冷凝管道的热分析[D]. 上海：上海交通大学，2008：11-21.

ZHANG S S. The thermal analysis of radiometer and HDPE pipe[D]. Shanghai：Shanghai Jiaotong University，2008:11-21(in Chinese).

[4] 肖庆生，杨林华，赵寿根.卫星红外遥感器辐射定标光机系统热-结构耦合变形分析[J]. 航天器环境工程，2011，28(1)：46-51.

XIAO Q S，YANG L H，ZHAO S G. Thermal-structure coupled deformation in an optical-mechanical system for radiometric calibration of satellite IR remote sensor[J]. Spacecraft Environment Engineering，2011，28(1)：46-51(in Chinese).

[5] NOEL C. Spatial prediction and ordinary Kriging[J]. Mathematical Geology，1988，20(4)：405-421.

[6] 王家华，余元华，高海余. 克里金地质绘图技术[M]. 北京：石油工业出版社，1999： 39-110.

WANG J H，YU Y H，GAO H Y. Beijing:Petroleum Industry Press[M]. Beijing：Petroleum Industry Press，1999：39-110(in Chinese).

[7] 彭思岭. 气息要素时空插值方法研究[D]. 长沙：中南大学，2010：5-16.

PENG S L. Developments of spatio-temporal interpolation methods for meteorological elements[D]. Changsha：Central South University，2010：5-16(in Chinese).

[8] MARCOTTE D. Cokriging with MATLAB[J]. Computers & Geosciences，1991，17(9)：1265-1280.

[9] MARTIN H T. Matlab Recipes for Earth Sciences[M]. German：Springer，2007：28-39.

[10] SIMPSON T W，BOOKER A J，GHOSH D，et al.Approximation methods in multidisciplinary analysis and optimization:a panel discussion[J]. Struct. Multidisc Optim.，2004，27(5)：302-313.

[11] DANIEL B，CHRIS L F，ARMIN I. Hierarchical nonlinear approximation for experimental design and statistical data fitting[J]. SIAM Journal on Scientific Computing，2007，29(1)：49-69.

[12] 李少华，刘远刚，王延忠. 泰森多边形在地质数据去丛聚中的应用[J]. 物探与化探，2011，35(4):562-564.

LI S H，LIU Y G，WANG Y Z. The application of Thiessen polygen to the declustering effect of geological data[J]. Geophysical & Geochemical Exploration，2011，35(4)：562-564(in Chinese).

(编辑：车晓玲)

Rapid thermal deformation analysis of on-orbit satellites on the basis of statistic method

ZHANG Yechi*，ZHANG Long，LUO Wenbo，PAN Teng

Beijing Institute of Spacecraft System Engineering，Beijing 100094，China

To calibrate the orientation position of the satellite orbit by the temperature sensors，the ordinary Kriging method widely used in geo-statistics was applied into the temperature estimation process of the satellite. A rapid thermal deformation analysis method was developed based on the statistic methods. Based on a small amount of temperature sensors，estimation of the temperature field was carried out. Then，the temperature field was used for the finite element analysis to accomplish the thermal deformation analysis. Differences between the analytical and the experimental results of the deformation of the payload are around 1′，which confirms that the method can be used to obtain the variation of optical axis of the payload. Furthermore，compared to the thermo physical method，the work period can be reduced by several days. This work provides guidance for rapid thermal deformation analysis of on-orbit satellites.

temperature measuring points；rapid thermal deformation analysis；statistic method; ordinary Kriging；variogram；finite element；satellite

10.16708/j.cnki.1000-758X.2016.0062

2016-03-29；

2016-06-17；录用日期：2016-08-22；

时间：2016-12-16 11:29:12

http:∥www.cnki.net/kcms/detail/11.1859.V.20161216.1129.007.html

战略性先导科技专项

张也弛，张龙，罗文波，等. 基于统计学方法的卫星在轨热变形快速分析[J].中国空间科学技术，2016，36(6)：

55-61.ZHANGYC，ZHANGL，LUOWB，etal.Rapidthermaldeformationanalysisofon-orbitsatellitesbasedontemperaturemeasuringpoints[J].ChineseSpaceScienceandTechnology，2016，36(6)：55-61(inChinese).

V414.3

A

http:∥zgkj.cast.cn

*通讯作者：张也弛(1983-)，男，博士，高级工程师，zhangyechi83@163.com，研究方向为航天器总体设计