一类非线性系统的函数观测器设计探究

张红钰,金玉苹,刁 瑞

（牡丹江师范学院数学科学学院,黑龙江 绥化 157000）

一类非线性系统的函数观测器设计探究

张红钰,金玉苹,刁 瑞

（牡丹江师范学院数学科学学院,黑龙江 绥化 157000）

本文着重对单边Lipschitz非线性系统函数观测器设计进行研究，在已知条件背景下，通过线性矩阵不等式对函数观测器增益矩阵条件进行明确，继而确定了函数观测器增益矩阵设计方法。以一个仿真实例为基础，对函数观测器的设计进行验证，既能够实现系统状态估计，又能够有效消除观测误差。

非线性;系统;函数观测器;设计探究

1 前言

非线性系统观测器设计问题一直备受关注，相关研究者也尝试通过坐标变换法、类Lyapunov方法和扩展的Kalman滤波法等对不同设计方法进行探索，以推进状态反馈实施，为非线性系统观测器研究奠定良好的理论及技术基础。以一类Lipschitz非线性系统观测器设计为例，相关文献中对该非线性系统的相关条件进行明确界定，有助于实现观测器渐近稳定，与此同时，也对观测器增益矩阵的设计方法进行明确，并在降维观测器设计中对相关研究成果进行推广。

Lipschitz条件背景下的观测器增益矩阵设计方法比较保守，数学领域研究者采用单边Lipschitz条件，对它的保守性进行有效控制。相关文献中已经对单边Lipschitz条件的概念进行了相关界定，且单边Lipschitz非线性系统观测器增益矩阵条件也比较充分，但是观测器增益矩阵设计过程中的有效性不足，也并未给出具体的设计方法。相关研究人员对线性矩阵不等式进行求解，以得出观测器增益矩阵。而单边Lipschitz非线性系统降维观测器增益矩阵的相关条件也比较充分，并尝试提出新型观测器设计方法。采用二次内积有界性使观测器增益矩阵条件充足，它需要对非线性矩阵不等式进行求解，笔者对该条件进行升级和改进，使其变为解线性矩阵不等式，而观测器增益矩阵设计方法属已知条件。借助Lyapunov方法，观测误差渐近稳定条件呈已知状态，对观测器设计进行转化，使其变为对线性矩阵不等式进行求解，借助该种方法，实现观测器增益矩阵设计。相关文献中，以代数Riccati方程为前提，对单边Lipschitz非线性系统降维和全维观测器设计方法进行明确。部分文献是基于状态观测器给出单边Lipschitz非线性系统观测器设计，而针对此类非线性系统函数观测器的设计仍然比较模糊。控制工程背景下，函数观测器是指重构状态反馈的函数所属观测器。部分函数的状态反馈直接重构，极有可能导致观测器尾数少于降维背景下的观测器维数，故而需要研究单边Lipschitz非线性系统函数观测器。本文着重对单边Lipschitz非线性系统函数观测器设计问题进行研究和考量，在线性矩阵不等式基础上，对函数观测器的存在条件进行明确，然后对函数观测器增益矩阵进行有效设计。

2 系统描述和预备知识

如下所示，为已知非线性系统：

x∈Rn指代系统状态，y∈Rn和u∈Rn分别指代输出和输入。而已知实矩阵为A∈Rn×n和A∈Rn×n，φ（x,u）属于连续的非线性函数。

从相关文献中得出如下定义：定义1 D指代的是包含原点的区域，假定ρ∈R属于已知存在条件，需对任意x1和x2∈D,

有关ρ的单边Lipschitz函数即对称函数φ（x,u），其中，单边Lipschitz常数是ρ，它比较灵活，可以以零、正数、负数三种状态存在，而条件（2）属于单边Lipschitz的条件。

3 设计函数观测器

依据非线性系统（1），执行函数观测器设计：

Z指代的是r×(n+p)维的任意矩阵。已知

故而矩阵Q∈Rr×r存在，由S∈Rr×p得出下列式子：

r×(r+p)维的任意矩阵是X。已知

属于行满秩矩阵，那么矩阵K的伪逆是K+=KT（KKT）-1，且

定理1 对系统（1）进行考量，假定包含的常数有ρ、α、β∈R，而非线性函数φ（x.u）与条件（2）和（3）相符合，行满秩矩阵K∈Rr×n，如果矩阵Z∈Rr×(n+p)存在，条件（8）成立。同时，矩阵P=PT＞0，X，和常数ε1和ε2在下列线性矩阵不等式中成立：

因而观测误差动态方程符合

从最受欢迎的课程来看，CCtalk的课程主要是面向初学者。另外，在能力考方面占很大比重，说明很大一部分人选择通过CCtalk这个平台提高能力考方面的知识。

在式子（17）中，对系统（1）和（4）进行代入，得出

与引理1条件相符合，可用下列式子对误差动态方程（18）进行表示：

其中Q=M1+XN1。

择定Lyapnnov函数

则闭环系统轨线背景下V(e)的导数为

针对任意正数ε2，

根据式子（21）、（22）和（23）得出

定理1得证[3]。

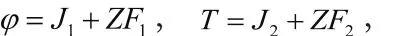
（2）对矩阵Z∈Rr×(n+p)进行验证，看其能否使条件（8）成立。如果成立，进入下一步，反之，重新验证。

（3）依据式子（12）分别对矩阵M1和M2以及N1和N2进行计算，并依据定理1，对线性矩阵不等式（15）进行求解。

（4）如果有矩阵P，X1=PX以及正数ε1和ε2都能够满足线性矩阵不等式（15），故而X=P-1X1，Q=M1+XN1，S=M2+XN2，表明完成函数观测器增益矩阵的设计。

4 仿真实例

已知行满秩矩阵，将Z设定为0，依据定理1对函数观测器进行设定，分别得出P、φ和T的矩阵。状态x2和x4的误差响应曲线和其初始值都处于已知状态，得出仿真结果，而6S内状态x2和x4的误差响应曲线能够收敛为0。已知矩阵K=I4，函数观测器（4）的类别是全维观测器，已知状态x2和x4的误差响应曲线，5S内其能够收敛为0[4]。

5 结语

本文着力于对单边Lipschitz非线性系统函数观测器设计等进行研究，在具体研究过程中，对线性矩阵不等式进行求解，继而得出函数观测器增益矩阵的成立条件。假定矩阵K的秩与状态维数相比较小，该背景下的函数观测器将具备降维观测器功能；如果矩阵K的秩与状态维数相等，函数观测器具备全维观测器功能。在专业范畴内进行一系列实验论证，得出的仿真结果证明了该设计方法极为有效，符合具体设计要求，有助于实现功能上的突破，对非线性系统函数观测器设计极具推动作用。

[1]高虹,蔡秀珊.一类非线性系统的函数观测器设计[J].控制理论与应用,2013(09)：1207-1210.

[2]蔡秀珊,王贞芸.单边Lipschitz非线性时滞系统的函数观测器设计[J].控制与决策,2015(12)：2259-2264.

[3]王璐,徐慧玲.一类3--D非线性系统的稳定性分析及函数观测器设计[J].控制理论与应用,2014(04)：493-500.

[4]孙蓉,刘胜等.一类非线性系统故障诊断观测器设计[J].控制理论与应用,2013(11)：1462-1466.

项目名称：牡丹江师范学院青年科研项目“不确定拟单边Lipschitz非线性系统观测器设计”。项目编号：QN201623

10.16640/j.cnki.37-1222/t.2016.22.241

张红钰（1982-），女，黑龙江绥化人，硕士研究生，讲师，研究方向：概率论与数理统计。