中考规律类试题解题策略探讨

刘丽霞

摘 要：从抓住题目中变量，进行尝试计算；理解一种新的定义方式，进行套用；根据所给数式，进行归纳猜想；抓住几何图形变化规律，列表归纳四方面进行探讨，以培养学生的观察、分析、比较、归纳、猜想、推理的能力。

关键词：中考；数学；规律类试题；解决问题

中图分类号：G424.79；G633.6 文献标志码：A 文章编号：1008-3561（2016）03-0080-01

西藏从2008年开始，每年的中考试题中，规律类试题频频出现，它往往给出了一组变化的数、式子、图形或条件，要求学生通过阅读、观察、分析、猜想来探索规律，主要考查学生的分析、观察、猜想、归纳能力以及探究、创新能力。现撷取2008年以来西藏中考题中的部分试题，说明此类题型的常用解法。

一、抓住题目中变量，进行尝试计算

这类题目一般是按一定规律排列的一列数之间的相互关系或大小变化规律的问题，主要通过观察、分析、归纳、验证，然后得出规律。以一列代数式即函数关系式为主要内容，考查的是找规律——数字的变化，通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况。解答此类问题的关键是仔细分析所给数字的特征得到规律，再把发现的规律应用于解题即可。

二、理解一种新的定义方式，进行套用

即给出一个同学们从未接触过的新定义，然后要求学生照着套用。这类题型主要考查学生的阅读理解能力、应变能力和创新能力。解这类试题的关键是，正确理解新定义，并将此定义作为解题的依据，同时熟练掌握教学中的基本概念和基本的性质。以上两种规律类试题形式相对简单，难度较低，对学生来说并不难，但观察是非常重要的，只要学生能够仔细观察，便不难现其中蕴含的规律。同时，教师在平日教学中应尽可能地多锻炼学生的观察、思考和发现问题的能力。

三、根据所给数式，进行归纳猜想

即给定一些代数式、等式或不等式，猜想其中蕴含的规律，一般先写出代数式的基本结构，然后通过横向或纵向对比，找出各部分特征，从而解答问题。例1 （2009年）：观察下列等式：（1）32-12=4×2；（2）42-22=4×3； （3）52-32=4×4； ……则第5个等式为 。分析：此类题目需通过仔细分析、归纳、猜想，发现其中的规律，属难度适中题目。对于此类题目，学生只有观察每个式子之间的特点、每个式子中的每个数的特点等，才能准确找到其规律。解答：观察每个等式的左边都是两个数的平方差，等号的右边都是数字4与一个数相乘；等式左边中第二个数是每个式子所在位数值的平方，第一个数是比第二个的数多2的平方，由此，不难发现第5个等式的左边是72-52，再观察等式右边都是4与一个数的乘积，且第2个数比位数值多1，故第5个等式为72-52=4×6。

四、抓住几何图形变化规律，列表归纳

即观察图形变化过程的特点，分析其中的联系和区别，用相应的算式由特殊到一般描述其中的规律。例2 （2010年）：如图，第1个图形由5个小正方形组成，第2个图形由9个小正方形组成，第3个图形由13个小正方形组成……以此规律，第n个图形由 个小正方形组成。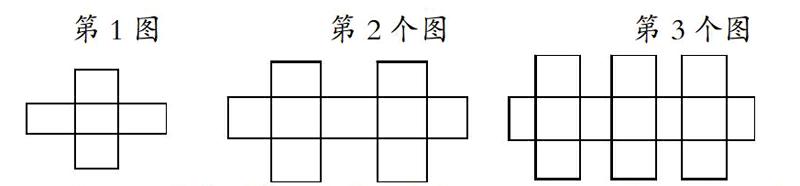

分析：这类规律题，对学生来说是难度最大的，解决这种问题的关键还是在观察的基础上找出各部分的共性，即始终遵循“寻找共性——寻找特性中的共性”这一原则，操作便有章可循，通常可以利用列表法解决。解答一：本题要先通过观察、分析，由第1个、第2个、第3个图形中小正方形的个数，来猜想、探求规律，求出第n个图形中小正方形的个数，列表如下：

通过小正方形的个数与图形序号，比较分析知，第n个图形中小正方形的个数为4n+1。解答二：通过观察发现，第1个图形有5个小正方形组成，第2个图形是在第1个图形的基础上又拼接了一个图形1，这样就重合了一个小正方形；同样第3个图形是在第2个图形的基础上又拼接了一个图形1，这样又重合一个小正方形，依此类推，可得第n个图形中小正方形的个数为：5n-（n-1）=4n+1。归纳以上可以知道，规律探究性试题主要考查学生自学能力和阅读能力、知识迁移能力、加工和利用信息的能力。但是“观察”是解决规律类试题的突破口，学生只有学会观察，并将观察形成一种习惯，才能灵活应对规律类试题中的各种题型。

五、结束语

在西藏中考中，规律型试题分值并不多，只有3分，但因这类题涉及的知识面和思想方法很多，且也非常注重理解，对学生各方面的发展是有很大益处的。况且，近几年中考数学重点考查学生的数学思维能力已经成为趋势和共识。因此，教师首先要在紧跟时代步伐的同时，在教学中也要大胆改革，课堂上要充分相信学生，给予学生充足的思考时间，依据数学本身的特点及学生对数学普遍不感兴趣的现状，不断有意识地培养学生的观察、分析、比较、归纳、猜想、推理的能力。同时，在进行专题复习时要加强这方面的力度，注重对学生从“特殊到一般，从抽象到具体”思想培养，会更有利于激发学生的学习兴趣，从而不断提高学生的综合素质。

参考文献：

[1]荣彬.新课标下数学中考命题趋势与解题关系的研究[D].四川师范大学，2014.

[2]申德全.中考试题中应用题新类型及解题策略[J].中学数学教学参考，2007（14）.