曲面论高斯方程公式的几种形式的推导方法
2016-01-29
邢家省1,高建全2,罗秀华2
(1.北京航空航天大学数学与系统科学学院,数学、信息与行为教育部
重点实验室,北京 100191;2.平顶山教育学院,河南 平顶山 467000)
曲面论高斯方程公式的几种形式的推导方法

邢家省1,高建全2,罗秀华2
(1.北京航空航天大学数学与系统科学学院,数学、信息与行为教育部
重点实验室,北京 100191;2.平顶山教育学院,河南 平顶山 467000)
摘要:考虑曲面论高斯方程公式的表示问题.运用曲面上基本方程的矩阵表示法,给出高斯方程直接的显式公式表示;指出高斯曲率简化公式的推导来源,揭示出高斯曲率隐式公式的发现过程,并给出了Liouville形式的高斯方程的证明过程.
关键词:曲面论基本方程;矩阵表示法;高斯方程;Liouville形式
曲面上的高斯曲率的定义和计算公式是经典曲面论的重要内容[1-12].曲面上的高斯曲率是曲面的内蕴量[1-6],这个重要结果是高斯于1827年发现的著名定理,称为高斯绝妙定理[2,6]或曲面论的高斯方程.该定理的原始表述形式是用曲面上的第1类基本量的隐式表达的.给出高斯方程的显式表达,是人们所追求的,而现有文献中给出的推导过程相当繁杂,不利于理解和掌握.笔者发现采用曲面论基本方程的矩阵表示法,运用矩阵运算就可以很简明地推导出高斯方程的显式表达[12].对正交曲线坐标网下高斯曲率的简化计算公式[1-6],笔者也给出了导致发现的过程.高斯曲率是内蕴量的隐式公式[1-7,9],人们通常都是采用验证的方式[7,9],没有指出这种公式是如何合理发现的,笔者给出了导致发现的推导过程.对Liouville形式的高斯方程也给出了推导过程[5].
1曲面论的基本方程的矩阵方程表达形式
给出C3类的正则曲面Σ:r=r(u1,u2),(u1,u2)∈Δ.按照文献[1-6,9-11]中的符号体系,给出如下一系列记号:

命

是A=(gij)的逆矩阵;
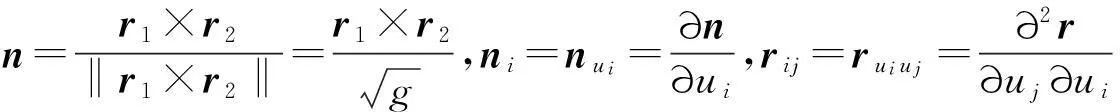

将曲面的基本方程改写成矩阵方程的形式为[1-6,9-12]:

(1)

(2)
其中
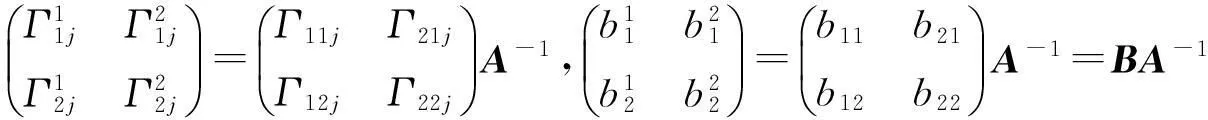
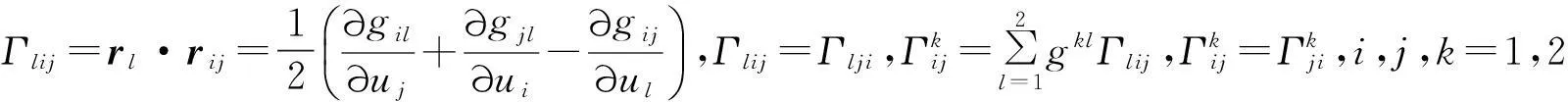
2曲面的基本方程中系数矩阵之间的关系的矩阵推导方法

利用(1)式,存在可解曲面的充要条件是
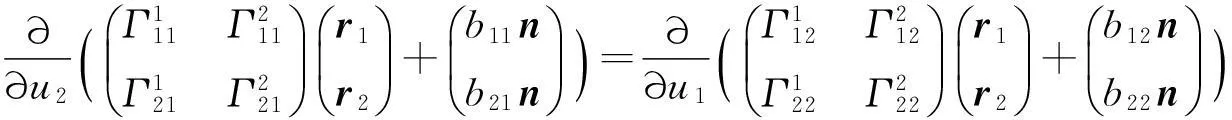
经过代入运算,最后比较左右两端的系数,可得
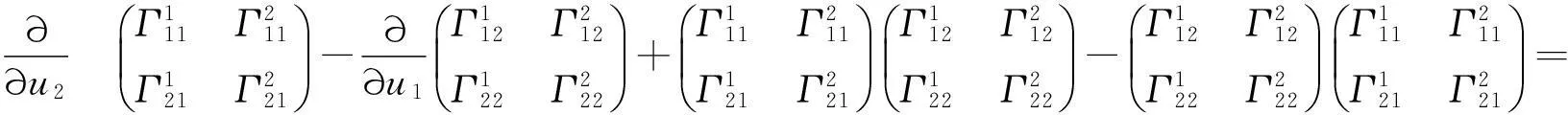
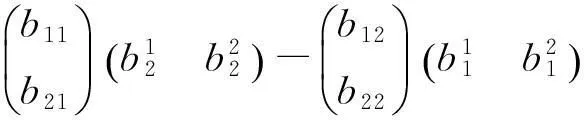
(3)
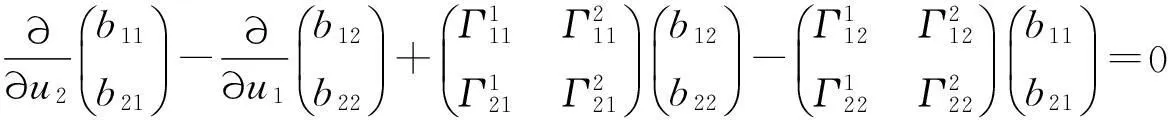
3高斯方程的隐式表示公式的矩阵推导方法
对(3)式右端进行代入运算[11-12],可得
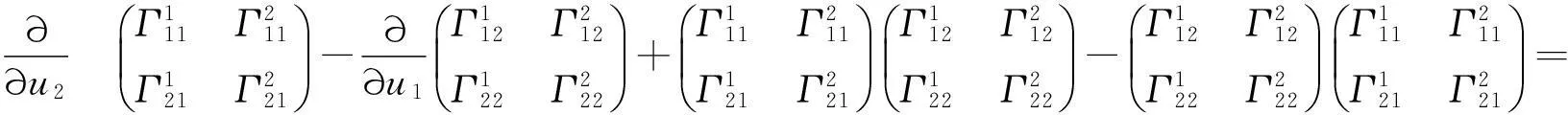
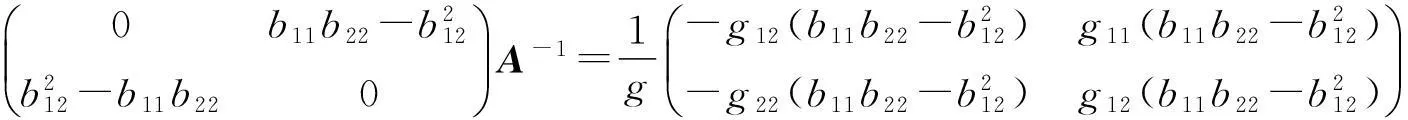
(4)
由(4)式两边矩阵中右上角的元素对应元素相等,可得[1-6,9,11]
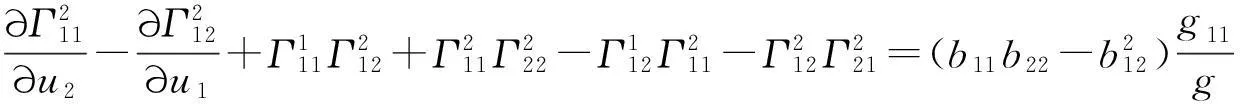
于是高斯曲率有如下的内蕴计算公式[1-6,9]:

(5)
由(5)式两边矩阵中左下角的元素对应元素相等,可得

于是高斯曲率有如下的内蕴计算公式[1-6,9,11]:
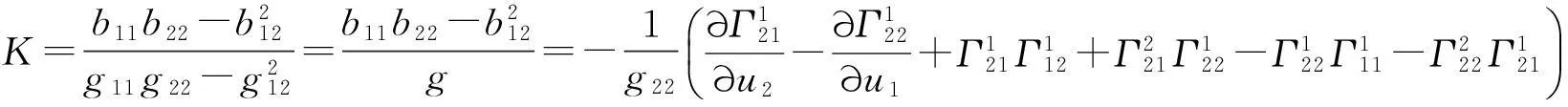
比较(4)式中两边矩阵中的对应元素相等,还可得到另外2个形式的等式[1-4].
4高斯方程的显式表示公式的矩阵推导方法
在(4)式左端利用曲面基本方程中系数矩阵的关系,经过代入运算[11-12],可得(4)式等价于[11-12]
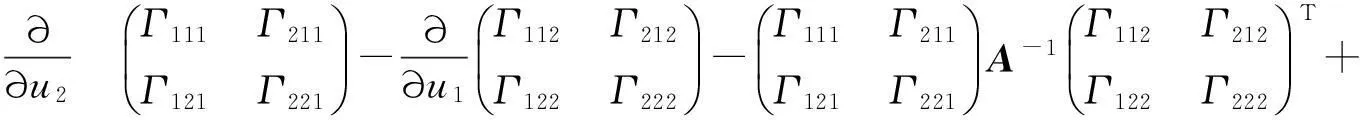
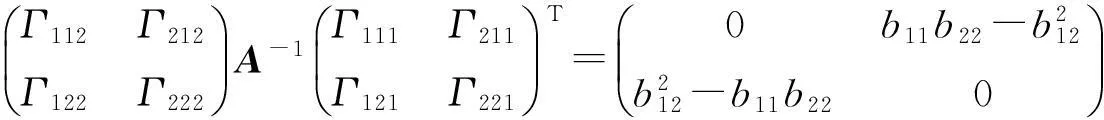
(6)
由(6)式两边矩阵的右上角对应元素相等,可得



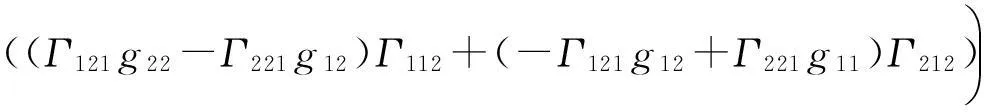
(7)
显然(7)式与高斯曲率内蕴定理的Brioschi表示公式是一致的[1-6,12].
利用

(8)
得出
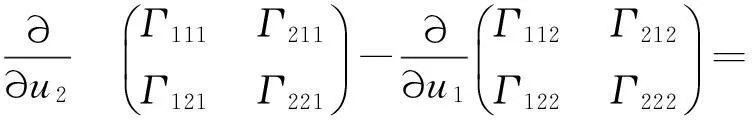

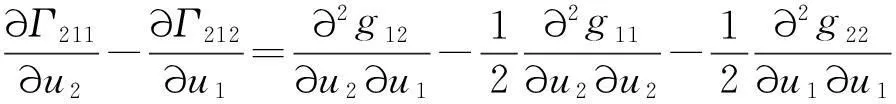
(9)

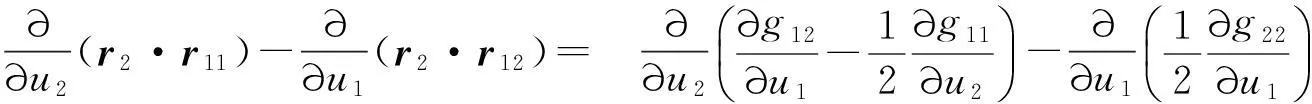
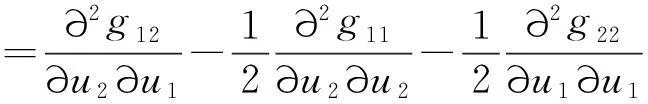
所以有
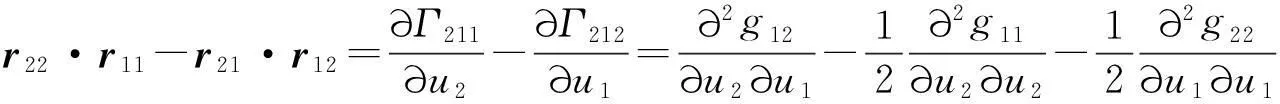
将(8),(9)式的对应项代入(7)式,经过计算化简,可得
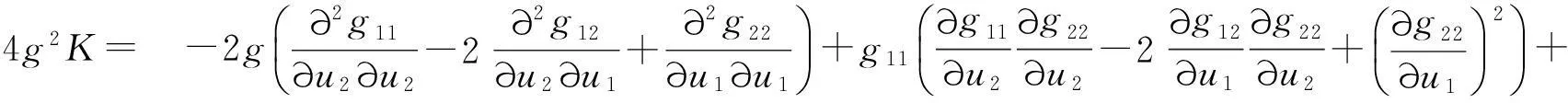


(10)
(10)式就是曲面论中著名的高斯方程[13],可以作为标准形式去验证其他形式.
5正交曲线坐标网下高斯曲率的简化计算公式的推导
当曲面Σ:r=r(u1,u2)上的坐标曲线网是正交网时,g12=r1·r2=0.利用(10)式,得到
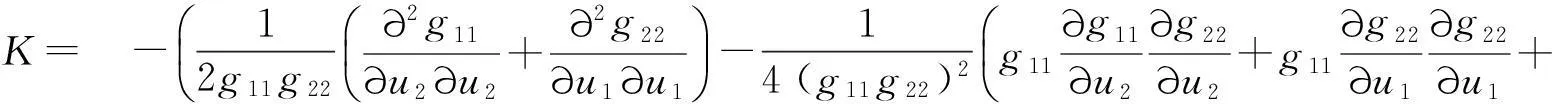
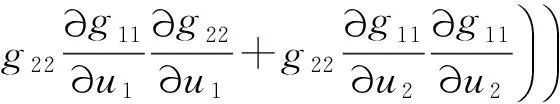
(11)
另一方面,经过凑微分法,逐步推导[12],可得


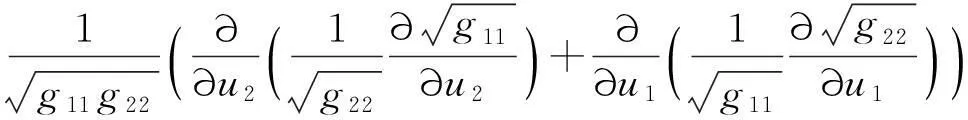
故有
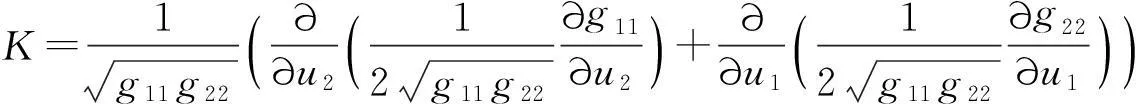
(12)

这就是正交曲线坐标网下高斯曲率的简化计算公式,具有重要的应用.
直接计算可得


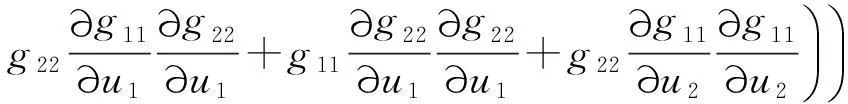
(13)
由(11)式和(13)式,得到

将(12)式改写为如下形式:
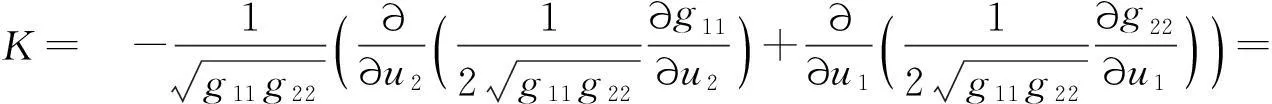
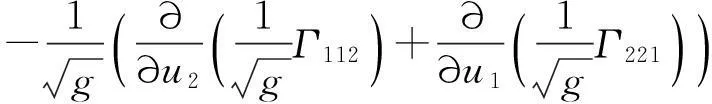
(14)
利用

得出
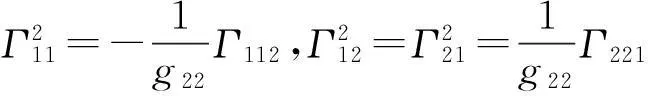
(15)
将(15)式代入(14)式,得


(16)
类似地,由
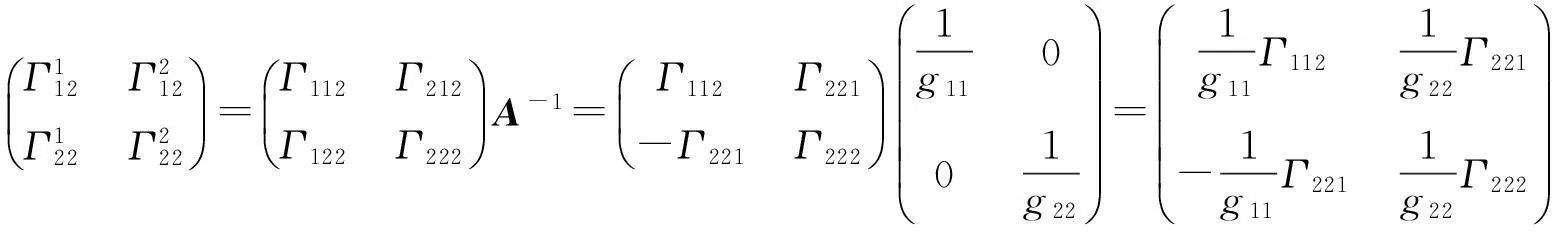
得到

(17)
将(17)式代入(14)式,得


(18)
对(16)式和(18)式,这里给出了导致其被发现的过程.
6高斯曲率隐式表示公式的来源及验证推导方法
在曲面Σ:r=r(u1,u2)上的曲线坐标网是正交网时,给出了对(16)式和(18)式的发现过程.
在一般坐标曲线网下,直接验证[1-2,7,9],成立

(19)
事实上,由

得到

(20)
将(20)式代入(19)式的右端,得到
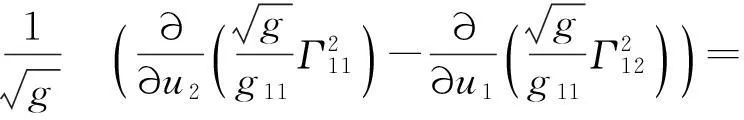
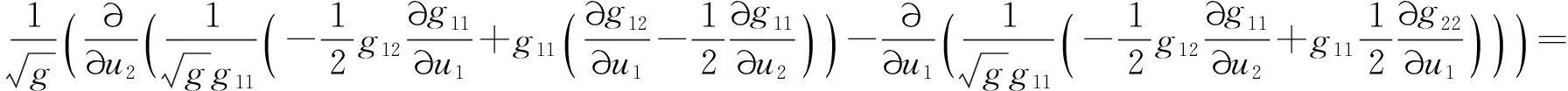

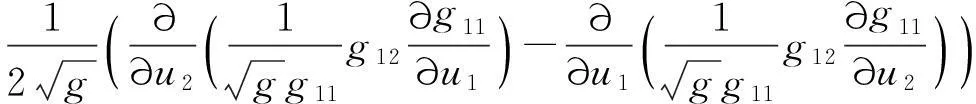
(21)
对(21)式经过求偏导数计算,可以得出(21)式与(10)式是相同的,于是(19)式成立.
类似地,在一般坐标曲线网下,直接验证[1-2,7,9,11],成立

(22)
事实上,注意到

(23)
将(23)式代入(22)式的右端,得到

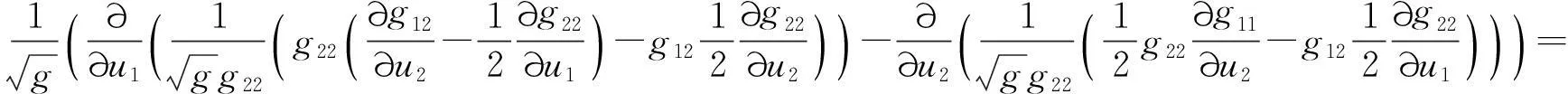


(24)
对(24)式经过求偏导数计算,可以得到与(10)式同样的式子,从而(22)式成立.
在一般坐标曲线网下,对高斯曲率的计算公式(19)式和(22)式,文献[1-7,9,11]中仅是直接给出,然后是验证法,没有给出是如何导致发现这种结果的,这里给出了来源.显然,在一般坐标曲线网下,(14)式不再成立.
7Liouville形式的高斯方程的发现推导过程
在曲面Σ:r=r(u1,u2)上的坐标曲线网是一般网的情形下,文献[5]中指出高斯方程有如下的Liouville形式:
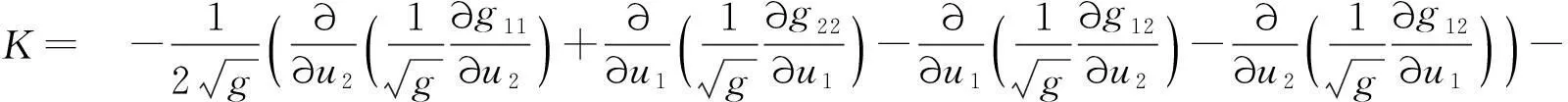

(25)
欲证(25)式成立,方法一是直接验证(25)式的右端与(10)式的形式一样,然而这没有指出(25)式本身是如何发现的.下面给出(25)式的发现性推导过程.
将(21)式和(24)式的两端相加,得到
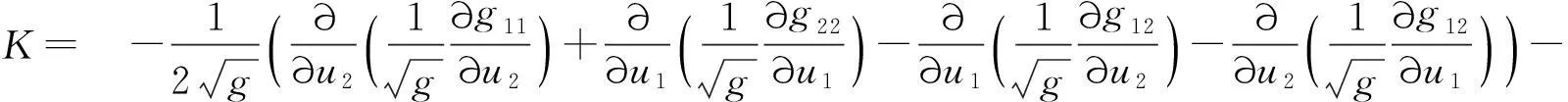

(26)
经过求偏导数运算及化简,可得到


(27)

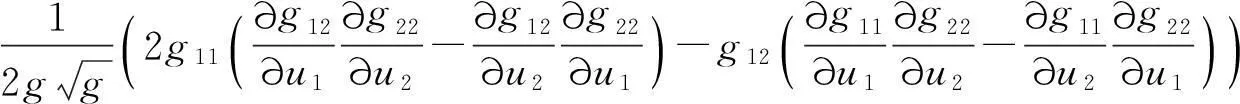
(28)
将(27)式和(28)式相加,得到
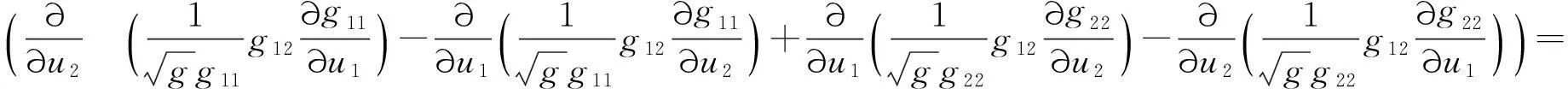
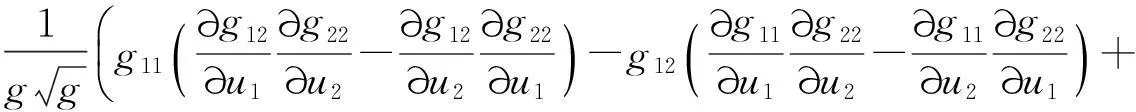

(29)
将(29)式代入(26)式,就得到(25)式成立.
参考文献:
[1] 梅向明,黄敬之.微分几何[M].第4版.北京:高等教育出版社出版,2008:87-105.
[2] 陈维桓.微分几何[M].北京:北京大学出版社,2006:193-228.
[3] 彭家贵,陈卿.微分几何[M].北京:高等教育出版社,2002:74-85.
[4] 苏步青,华宣积,忻元龙.实用微分几何引论[M].北京:科学出版社,1986:91-94.
[5] 王幼宁,刘继志.微分几何讲义[M].北京:北京师范大学出版社,2003:149-153.
[6] 陈维桓.微分几何例题详解和习题汇编[M].北京:高等教育出版社出版,2010:171-219.
[7] 曾宪祖.高斯曲率的一个计算公式的证明[J].云南师范大学学报,1991,11(4):52-53.
[8] 邢家省,王拥军.曲面上法曲率的最值和最值切方向的性质[J].吉首大学学报:自然科学版,2013,34(1):6-10.
[9] 邢家省,张光照.曲面基本方程的性质及其应用[J].聊城大学学报:自然科学版,2013,26(3):7-12.
[10] 邢家省,张光照.曲面上曲线的测地曲率向量的注记[J].吉首大学学报:自然科学版,2013,34(4):7-10.
[11] 邢家省,高建全,罗秀华.曲面论基本方程的矩阵推导方法[J].吉首大学学报:自然科学版,2014,35(3):4-10.
[12] 邢家省,高建全,罗秀华.高斯曲率内蕴公式的几种形式的推导方法[J].四川理工学院学报:自然科学版,2014,27(4):82-89.
[13] 华罗庚,著.高等数学引论(第2册)[M].王元,校.北京:科学出版社,2009:301-322.
(责任编辑向阳洁)
Derivation of Gaussian Equation figures of Surface Theory
XING Jiasheng1,GAO Jianquan2,LUO Xiuhua2
(1.Department of Mathematics,LMIB of the Ministry of Education,Beihang University,Beijing 100191,China;
2.Pingdingshan Institute of Education,Pingdingshan 467000,Henan China)
Abstract:The Gaussian equation expression of surface theory is discussed.The direct explicit figure expression of Gaussian equation is derived by means of the matrix expression of the fundamental equation on curved surface.The derivation of Gaussian curvature simplified figure is discussed which discloses the discovery of Gaussian curvature implicit figure.The proof procedure of Gaussian equation of Liouville form is demonstrated.
Key words:fundamental equation of surface theory;matrix expression;Gaussian equation;Liouville form
作者简介:邢家省(1964—),男,河南泌阳人,北京航空航天大学副教授,博士,主要从事偏微分方程、微分几何研究.
基金项目:国家自然科学基金资助项目(11201020);北京航空航天大学校级重大教改项目(201401)
收稿日期:2014-08-01
中图分类号:O186.1
文献标志码:A
DOI:10.3969/j.issn.1007-2985.2015.02.001
文章编号:1007-2985(2015)02-0001-07
