贝叶斯公式及其应用的教学研究

李春娥，王景艳

(保山学院数学学院,云南保山678000)



贝叶斯公式及其应用的教学研究

李春娥，王景艳

(保山学院数学学院,云南保山678000)

[摘要]通过贴近生活的例子，引入贝叶斯公式，然后，介绍信用问题和在生产中的索赔问题介绍贝叶斯公式的实际应用，以使在教学中能帮助学生更深入地理解该公式.

[关键词]贝叶斯公式； 应用； 教学研究

贝叶斯公式是英国学者托马斯·贝叶斯(Thomas Bayes,1702-1761)最早发现的,首次发表在1763年,当时贝叶斯已经去世,其结果没有受到应有的重视.1774年,法国数学家拉普拉斯(Laplace P S, 1749-1827)再一次总结了这一结果.此后,人们逐渐认识到这个著名概率公式的重要性.[1]现在,它已在疾病诊断、信用、生产、承担经济责任、收发信息问题和解释生活谚语等方面发挥着重要的作用.

1由生活中的现实问题引入概念

引例设马航MH370飞机坠落在甲、乙、丙三个区域之一，营救部门判断其概率分别为b1,b2,b3.用直升机搜索这些区域，若有残骸，发现的概率分别a1,a2,a3，试在直升机搜索过三个区域均未发现残骸的情况下，求飞机落入甲、乙、丙三个区域的概率.

解设A表示直升机在甲、乙、丙三个区域未发现残骸，B1,B2,B3分别表示飞机落入甲、乙、丙三个区域，由题意知

P(B1)=b1，P(B2)=b2，P(B3)=b3，P(A|B1)=1-a1，

P(A|B2)=1-a2，P(A|B3)=1-a3.

由条件概率公式和乘法公式知

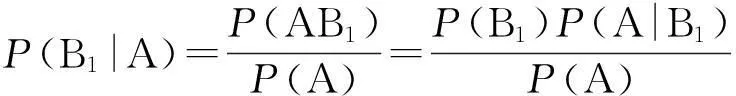
(1)

由全概率公式得

P(A)=P(B1)P(A|B1)+P(B2)P(A|B2)+P(B3)P(A|B3)

=b1(1-a1)+b2(1-a2)+b3(1-a3).

(2)

将(2)式代入(1)式得到，在直升机搜索过三个区域均未发现残骸的情况下，飞机落入甲区域的概率为

(3)

同理可得，在直升机搜索过三个区域均未发现残骸的情况下，飞机落入乙、丙两个区域的概率分别为

(4)

(5)

引例中采用的方法是概率论中重要的方法之一，为了求某一事件的条件概率，即当观察到一个事件已经发生时，去求导致所观察到的事件发生的各种原因、情况或途径的可能性大小，利用条件概率公式、乘法公式和全概率公式，得到(3)式，将(3)式一般化便得到了贝叶斯公式.

2贝叶斯公式

定理[2]设试验E的样本空间为S，A为E的事件，B1，B2，…，Bn为S的一个划分，且P(A)>0,P(Bi)>0(i=1,2,…,n)，则

(6)

(6)式称为贝叶斯(Bayes)公式．

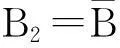
3贝叶斯公式的应用

Bayes公式的应用步骤：

(i)把事件A看作某一过程的结果；

(ii)把B1, B2, …, Bn看作该过程的n个原因；

例1(信用问题)某商业银行对在校贫困大学生进行助学贷款，某大学生承诺毕业三年内还清助学贷款，否则视该生不遵守承诺(撒谎).假设我们对该生的信任程度为0.8，可信的学生不遵守承诺的概率为0.1，不可信的学生不遵守承诺的概率为0.95，若该生在毕业三年内未还清贷款，求银行对该生的信任程度为多少？

解事件A表示该生不遵守承诺，事件B表示该生可信，依据题意知

由Bayes公式，求得该生在毕业三年内未还清贷款，银行对该生的信任程度为

可以得到，在该生不遵守承诺一次的情况下，银行对该生的信任程度降为0.30.这例子提示我们，该生在以后买房、买车等向商业银行贷款时，将有很大的可能遭到银行的拒绝.

例2[3](在生产中的索赔问题)从过去的资料中知，在出口罐头导致索赔事件中，有50%是质量问题，30%是数量短缺问题，20%是包装问题.又知在质量问题争议中经过协商解决不诉诸法律的占40%，数量问题中，经过协商解决的占60%，包装问题中经过协商解决的占75%.如果出一件索赔事件，在争议中经过协商解决了，问这一案件不属于质量问题的概率是多少？

解设B1={质量问题},B2={数量短缺问题},B3={包装问题},A={协商解决}，则

P(B1)=0.5,P(B2)=0.3,P(B3)=0.2,

P(A|B1)=0.4,P(A|B2)=0.6,P(A|B3)=0.75，

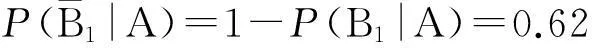
贝叶斯公式在概率论与数理统计中有着多方面的应用，如在疾病普查、经济决策、收发信号和破案中的应用，在这里不再一一举例.

4总结

用现实生活中的热点问题，激发学生的学习兴趣，引入贝叶斯公式.在课堂上，讲解信用问题，不仅加深了对贝叶斯公式的理解，还教育了学生要守信.贝叶斯公式在社会领域中应用广泛，讲解例题要达到举一反三的效果，使学生掌握住贝叶斯公式的实质.贝叶斯公式是在已知一事件发生下，重新认识导致该事件发生的原因事件的概率，即有了试验结果后对原因事件认识的调整.全概率公式是贝叶斯公式的一部分，“由因索果”用全概率公式，“由果索因”用贝叶斯公式.

[参考文献]

[1]杨静,陈冬,程小红.贝叶斯公式的几个应用[J].大学数学，2011，27(2)：166-166.

[2]盛骤, 谢式千, 潘承毅. 概率论和数理统计[M].北京：高等教育出版社，2009.

[3]李贤平，沈崇圣，陈子毅.概率论与数理统计[M].上海：复旦大学出版社，2003.

Bayesian figure and Its Applications in Teaching and Research

LIChun-e，WANGJing-yan

(Department of Mathematics，Baoshan College，Baoshan ,Yunnan 67800,China)

Abstract:Through close-life examples, the introduction of the Bayesian figure, and then introduce credit problems and production claims issues of practical application of Bayesian figure, which might help students better understanding of the figure in teaching.

Key words:Bayesian figure； the application； teaching and research

[基金项目]保山学院校级课题(14BY018)

[收稿日期]2014-07-20 2014-10-17

[中图分类号]O211

[文献标识码]C

[文章编号]1672-1454(2015)02-0119-03