一个多参数Hardy-Hilbert型不等式及应用
2016-01-28有名辉
有名辉
(浙江机电职业技术学院人文社科学院,浙江 杭州 310053)
一个多参数Hardy-Hilbert型不等式及应用
有名辉
(浙江机电职业技术学院人文社科学院,浙江 杭州 310053)
摘要:建立了一个多参数的Hardy-Hilbert型不等式,统一了一些已有的结论.作为应用,赋予参数不同的数值,文中还建立了若干已有不等式的对偶形式,并给出了一些新的、简洁的Hilbert型不等式.
关键词:Hardy-Hilbert不等式;多参数;推广;β-函数
收稿日期:2015-01-14
通信作者:有名辉(1982—),男,硕士,主要从事函数逼近论及解析不等式研究.E-mail:youminghui1@163.com
doi:10.3969/j.issn.1674-232X.2015.05.015
中图分类号:O178MSC2010: 26D15
文献标志码:A
文章编号:1674-232X(2015)05-0531-06
0引言与预备知识


(1)
不等式(1)是著名的Hardy-Hilbert重级数不等式[1],它在分析学及其应用领域有着重要的作用,其等价形式为
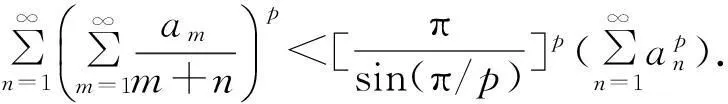
(2)
近年来,一些学者给出了不等式(1)的诸多推广.如2002年,杨必成在文[2]中证明了0<λ≤min{p,q}时:

(3)
2006年,杨又在文[3]中引进了β-函数,得到2-min{p,q}<λ≤2时:

(4)
2007年,孙保炬[4]证明了当λ>0,且0<α≤min{p,q}时:

(5)
显然式(5)是式(3)的推广,但不是式(4)的推广.2010年,刘琼等[5]又给出了式(5)的进一步推广,即α>0,0<λ1α≤min{p,q},0<λ2α≤min{p,q}时,有

(6)
注1从原文的证明看,条件“0<λ1α≤min{p,q},0<λ2α≤min{p,q}”应当修正为“0<λ1α≤q,0<λ2α≤p”.
不难发现,式(6)仍然不是式(4)的推广形式. 本文的目的是将建立式(6)和式(4)的统一推广形式, 并给出一些有意义的特殊结果.在此先给出相关引理.
1引理
引理1若α,λ1,λ2,c1,c2>0,0≤β1,β2<1,且λ1(1-β2)+λ2(1-β1)=αλ1λ2, 则
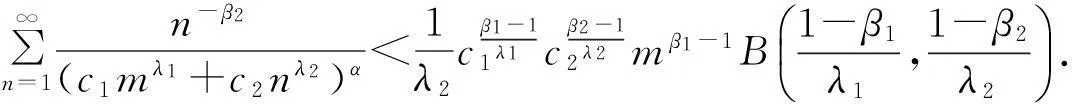
(7)
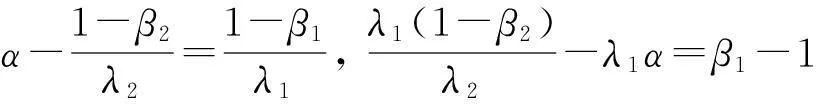
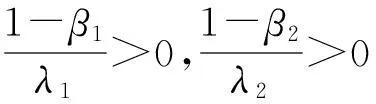


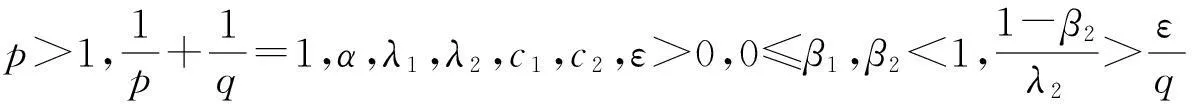
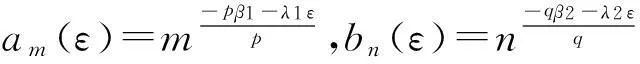

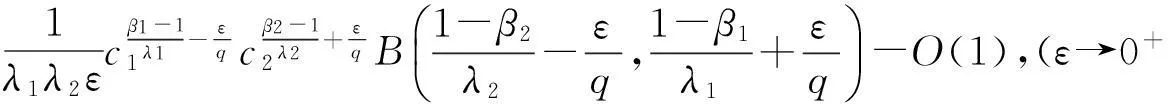
(8)

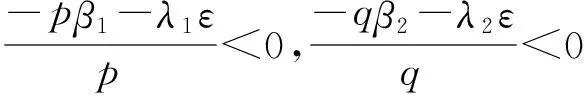

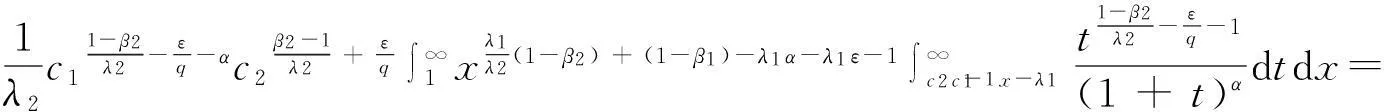
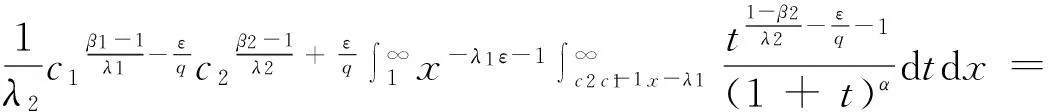
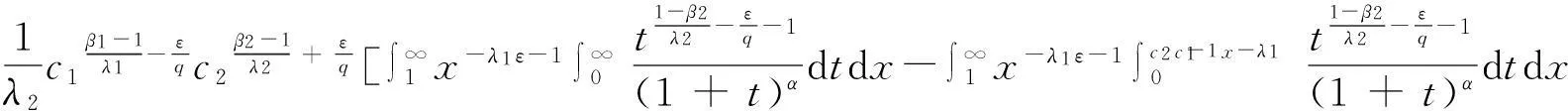
(9)

(10)
并且此时,有
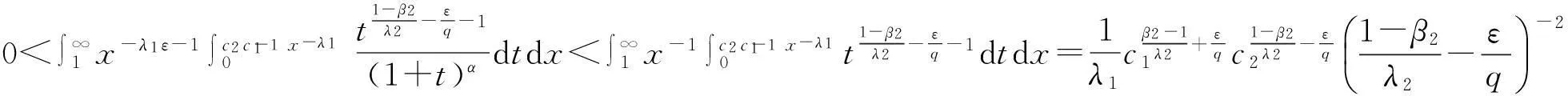
令ε→0+,可得

(11)
把式(10)(11)代入到式(9),易知式(8)成立.引理2证毕.
2主要结果及应用
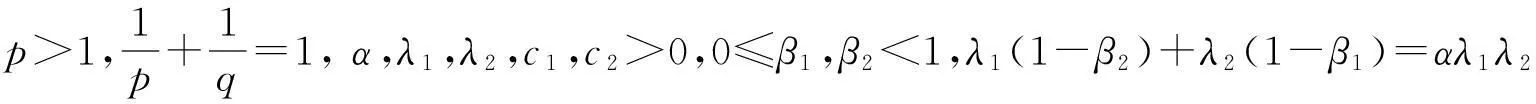
an,bn≥0(n∈N)满足,则
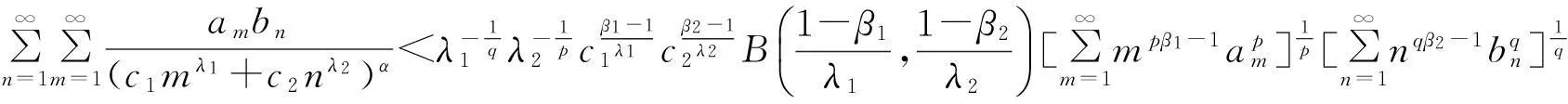
(12)
其等价形式为
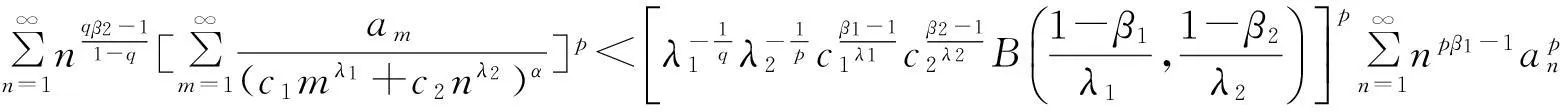
(13)
证明(Ⅰ) 首先证明式(12)成立.由Hölder不等式,可知
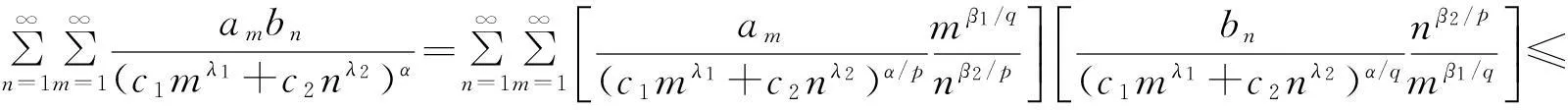
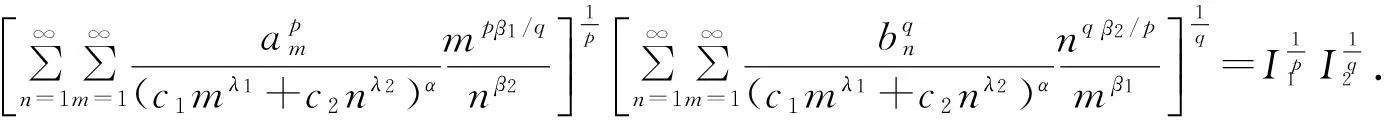
(14)
由引理1,可得
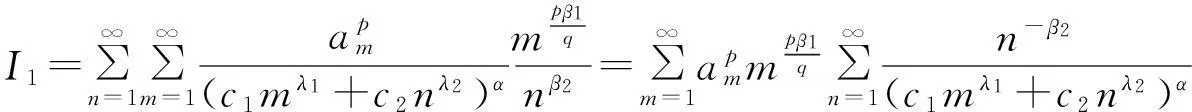

(15)
类似地,可算得

(16)
把式(15)(16)代入到式(14),便得式(12).
(Ⅱ)以下证明式(12)和式(13)是等价的.
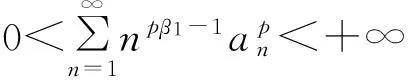

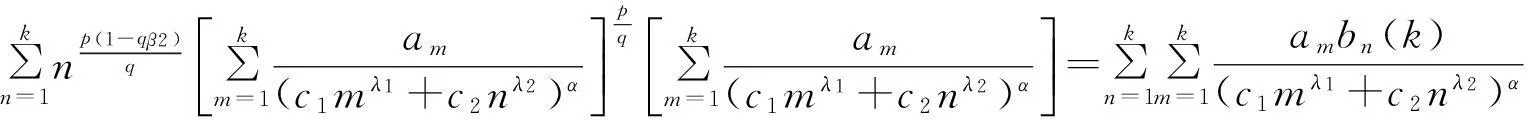
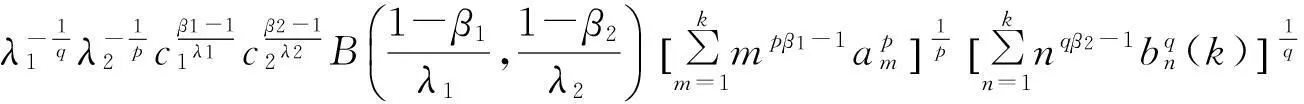
(17)
因此

(18)
要说明式(13)和式(12)等价,以下只需从式(13)证得式(12).事实上,由Hölder不等式,可知
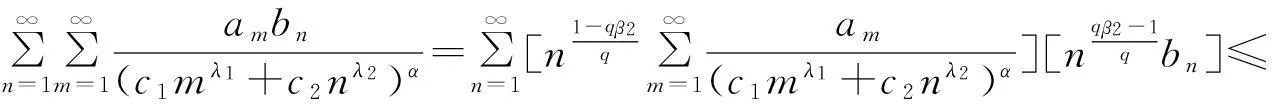


(19)
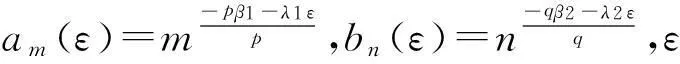

因为

所以
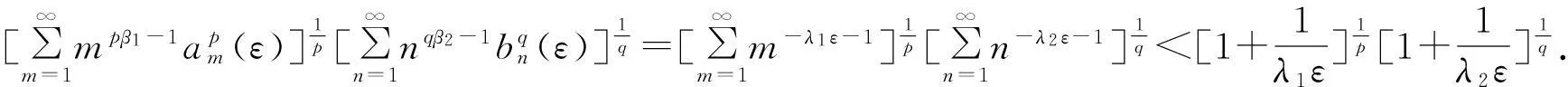
(20)
若式(12)中的常数因子不是最佳的,则存在正实数k,满足

使式(12)中的常数因子换成k后式(12)仍然成立.特别地,我们可以得到
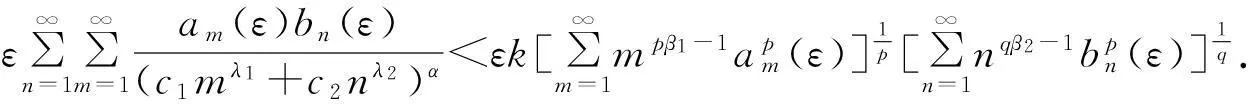
由式(8)和式(20),可知
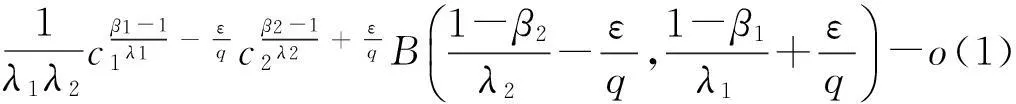
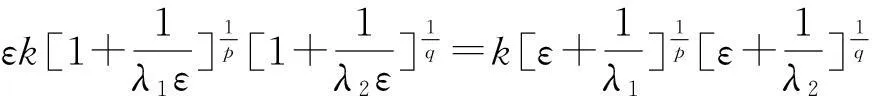
令ε→0+,则
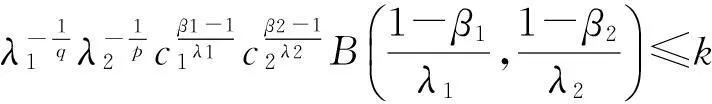
这与

矛盾.因此式(12)中的常数因子是最佳的.


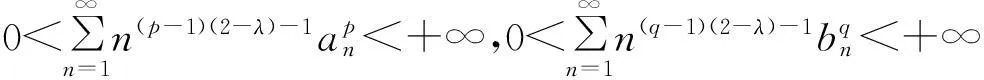
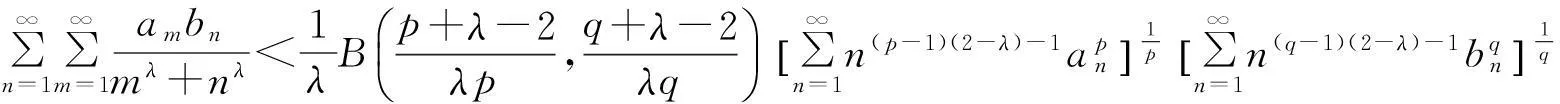
(21)
特别地,在推论1中,令λ=2,则式(21)转化为

(22)
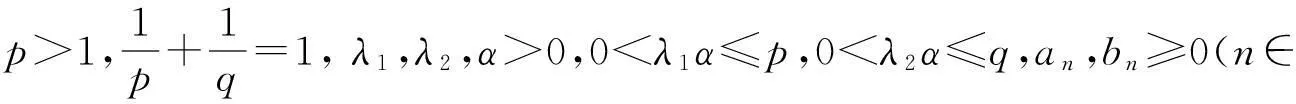
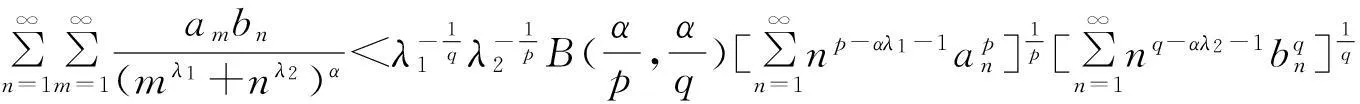
(23)
在定理1,令c1=c2=λ1=λ2=α=1, 则有
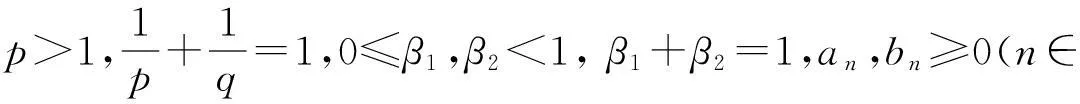
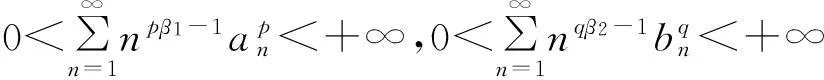
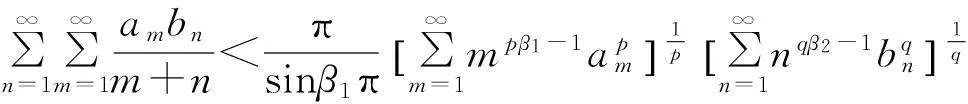
(24)
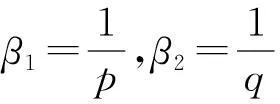
参考文献:
[1] Hardy G H, Littlewood J E, Polya G. Inequalities [M]. Cambridge: Cambridge University Press,1952.
[2] 杨必成.关于一个推广的Hardy-Hilbert不等式[J].数学年刊A辑,2002,23(2):247-254.
[3] 杨必成.关于Hardy-Hilbert不等式的单参数推广[J].数学的实践与认识,2006,36(4):226-231.
[4] 孙保炬.一个推广的具有最佳常数的Hardy-Hilbert不等式[J].数学进展,2007,36(1):39-46.
[5] 刘琼,李继猛.一个具最佳常数的多参数Hardy-Hilbert不等式[J].数学杂志,2010,30(5):877-882.
A Hardy-Hilbert Type Inequality with Multi-Parameters and its Applications
YOU Minghui
(School of Humanities and Social Sciences, Zhejiang Institute of Mechanical and Electrical Engineering, Hangzhou 310053, China)
Abstract:By establishing a new Hardy-Hilbert type inequality with multi-parameters, this paper unifies some known results. As the application, different values are given for the parameters, the dual form of some known inequalities is established, and some new and concise Hilbert-type inequalities are also presented.
Key words:Hardy-Hilbert’s inequality; multi-parameters; generalization; β-function

