圆柱形RC桥墩的弯矩-曲率曲线的研究

王　冲，胡文哲

(长安大学公路学院)



圆柱形RC桥墩的弯矩-曲率曲线的研究

王冲，胡文哲

(长安大学公路学院)

摘要：在RC桥墩结构的抗震设计中，必须考虑结构进入弹塑性变形阶段后的动力特性和动力性能，对桥墩的弯矩曲率曲线的研究就非常必要。主要研究轴压比和箍筋的体积配筋率(即配箍率)对曲率和弯矩的影响，为圆柱形RC桥墩的抗震提供参考。

关键词：钢筋混凝土桥墩；抗震设计；弯矩-曲率曲线

1概述

我国是世界上多地震的国家之一，在地震发生过程中，桥墩的破坏是其中的破坏之一，并且有可能导致桥梁的倒塌。钢筋混凝土桥墩结构的抗震设计就显得非常重要了。在钢筋混凝土桥墩结构的抗震设计中，必须考虑结构进入弹塑性变形阶段后的动力特性和抗震性能。应为桥墩的截面受到箍筋的套箍作用，将会提高截面混凝土的强度，另一方面钢筋屈服以后还要进入强化阶段。因此，桥墩截面屈服以后的实际强度是有一定程度提高的，所以对桥墩截面的弯矩-曲率曲线的分析是必须的。

2弯矩-曲率理论分析

桥墩的抗弯设计可以更合理地基于考虑了横向约束对混凝土受压应力—应变关系以及纵向钢筋应变硬化影响的弯矩-曲率分析来完成。在弯矩-曲率分析中使用的典型假设如下。

(1)平截面在变形后仍是平面。

(2)钢筋的本构关系已知。本文中钢筋的本构关系采用双折线模型。钢筋的弹性模量取Es=200GPa，屈服后刚度和屈服前刚度之比去0.01。

(3)混凝土的本构关系已知。本文中约束混凝土的本构关系采用Mander模型。

(4)混凝土和钢筋的合成轴力和合成弯矩与外部轴向荷载和弯矩平衡。

对于钢筋混凝土来说，通常把屈服弯矩定义为受拉钢筋开始屈服时的截面弯矩，极限弯矩定义为峰值弯矩抗弯能力处的弯矩。通常把极限曲率定义为，当混凝土边缘纤维应变达到它的极限应变时，或者当钢筋达到它的极限应变时的曲率。

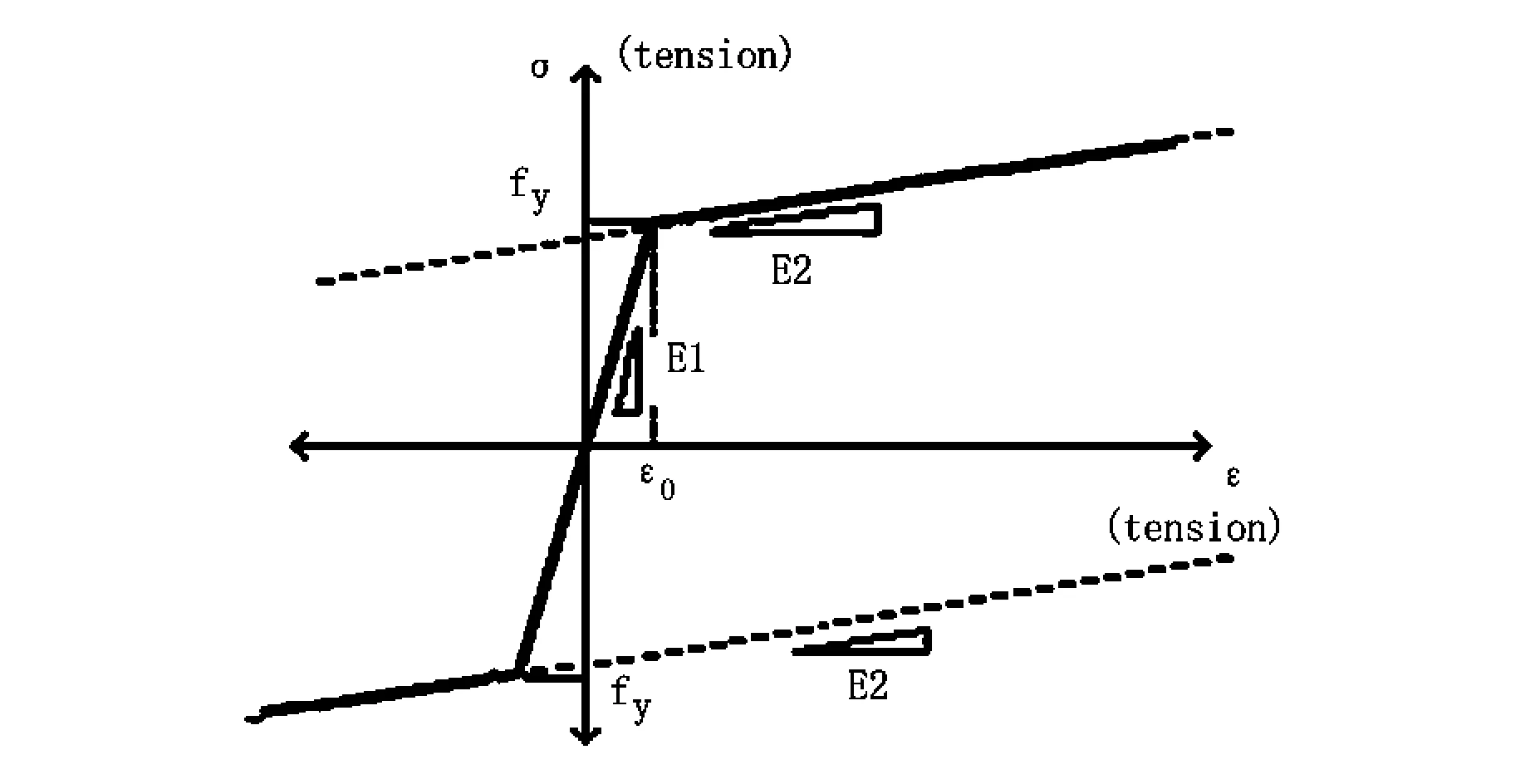
图1　钢筋的双折线模型

图2　混凝土的Mander模型

3计算分析

圆柱形RC桥墩的直径为1.3m，混凝土保护层厚度50cm。混凝土的标号为C30，混凝土的立方体强度fcu,k于美国和欧洲等国家所用圆柱体强度fc’之间的换算关系近似为fc’=0.8fcu,k。定义轴压比n=P/fcu,kA，其中P为轴力，A为毛截面积，fcu,k为混凝土的立方体强度。

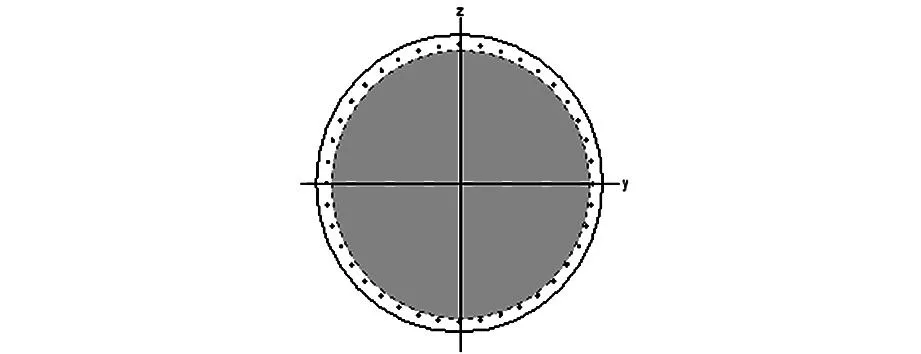
图3　圆柱形桥墩的截面

3.1　轴压比对弯矩和曲率的影响

在纵向钢筋的配筋率为1.3%，配箍率为0.5%的情况下分析轴压比对弯矩和曲率的影响。

图4　轴力-弯矩-曲率图

从上图可以看出，钢筋混泥土截面的轴力-弯矩-曲率关系具有如下特征：

(1)当轴压比较小时，轴力-弯矩-曲率关系具有明显的三折线特征，可采用以开裂点、屈服点和极限点为控制的三折线简化曲线来代表；当轴压比较大时，轴力-弯矩-曲率关系曲线不再具有三折线特征，没有明显拐点(甚至全截面受压没有开裂)，没有屈服平台，曲线较陡，极限曲率较小。

(2)当轴压比较小时，轴压比越大，截面的极限弯矩越大；当轴压比较大时，轴压比越大，截面极限弯矩越小。

(3)轴压比越大，截面极限曲率越小，曲率延性越小。

3.2　配箍率和轴压比对弯矩和曲率的影响

在纵向钢筋的配筋率为1.3%，分析配箍率对弯矩、曲率的影响。

表1　配箍率和轴压比对极限

表2　配箍率和轴压比对极限曲率(1/m)的影响

从上表可以看出：

(1) 在配箍率一定的情况下，极限弯矩随轴压比的增加先增加后减小，极限曲率随轴压比的增加而减小；这也验证了3.1里面的结论。

(2)在轴压比一定的情况下，极限弯矩随配箍率的增加而增加，极限曲率随配箍率的的增加而增加；但是增加的幅度是一直在减少。

(3)极限弯矩随配箍率的增加幅度随轴压比的增加而增加；极限曲率随配箍率的增加的幅度随轴压比的增加而减小。在配箍率超过0.8%以后，极限曲率几乎不再增加。

4结语

论述了圆柱形钢筋混凝土桥墩在轴压比和配箍率的变化下，弯矩和曲率的变化情况，为桥梁的抗震尤其是弹塑性分析研究提供了参考，为桥梁在大震作用下的响应提供理论支持。

参考文献：

[1]范立础. 桥梁抗震[M]. 上海: 同济大学出版社，1997.

[2]陈惠发，段炼. 桥梁工程抗震设计[M]. 北京：机械工业出版社，2008.

[3]过镇海. 钢筋混凝土原理[M].北京：清华大学出版社，1999.

作者简介：王冲(1992-)，男， 陕西咸阳人，硕士研究生，研究方向：桥梁抗震。

收稿日期：2015-01-28

中图分类号：U442

文献标识码：C

文章编号：1008-3383(2015)08-0122-01