水利工程群应对干旱能力定量评价研究:方法及案例*

王　刚，潘　涛，严登华，齐　珺，刘少华，赵继伟

(1.北京市环境保护科学研究院，北京100037；2. 东华大学 环境科学与工程学院,上海 201620；3.中国水利水电科学研究院水资源研究所，北京100038；4.华北水利水电大学 水利学院，河南 郑州 450045)



水利工程群应对干旱能力定量评价研究:方法及案例*

王刚1,2，潘涛1，严登华3，齐珺1，刘少华3，赵继伟4

(1.北京市环境保护科学研究院，北京100037；2. 东华大学 环境科学与工程学院,上海 201620；3.中国水利水电科学研究院水资源研究所，北京100038；4.华北水利水电大学 水利学院，河南 郑州 450045)

摘要:水利工程群是由区域上蓄、引、提、调工程及闸坝工程组成的复杂供水系统，是应对区域干旱的关键支撑。针对当前抗旱能力评价概念表达不统一、定量评价方法不完善等问题，对水利工程群应对干旱能力进行界定；从干旱本质和干旱灾害形成的机理出发，定义了干旱应对能力水平指数(HEGdca)，并提出基于HEGdca的水利工程群应对干旱能力定量评价方法。以2010年为评价水平年，评价了漳卫河流域给定水利工程条件应对不同程度气象干旱事件的能力。结果表明：以流域多年平均缺水率为衡量标准，漳卫河流域当前(2010年)的水利工程条件整体可以有效应对不超过30年一遇的干旱。评价结果与流域的实际情况相符，可为流域抗旱规划和干旱风险管理提供技术支撑。

关键词:水利工程群；干旱应对能力指数；定量评价；游程理论；水资源优化配置模型；漳卫河流域

干旱作为一种极端的水文水资源事件，长期以来制约着我国经济社会的发展[1-2]。水利工程群通过对水资源的时空调节，降低水源供水的不确定性，以满足不同用水户在复杂气候水文条件下的用水需求，是应对区域干旱和规避旱灾风险的关键途径之一[3-5]。我国旱情与旱灾的发生除了与气候变化、自然地理背景、水资源禀赋条件等因素有关外，还与我国水资源配置工程供水能力不足密不可分。围绕变化环境下干旱综合应对的实践需求，亟需回答两个方面的问题，即当前水利工程体系能够应对多大程度的干旱？如何通过优化调控提升工程应对干旱的能力？其中，评价是干旱应对的基础，调控是提升应对能力的重要手段。开展干旱应对能力评价研究可为明确防旱抗旱工作方向、干旱灾害风险管理提供重要支撑。

基于多指标的综合评价方法是当前抗旱能力评价研究中常用的，且较为成熟的一种方法[6-9]，但存在指标如何选取、权重的合理分配、抗旱能力等级划分等问题，且只能定性评价区域上干旱应对能力的相对强弱，而不能定量评价区域水利工程体系应对干旱的能力水平[10-11]。近年来，国内学者就区域抗旱能力定量评价方法开展了一些探索研究。如金菊良等[12]从塘坝灌区农业灌溉需水量与塘坝可供水量平衡的角度出发，提出塘坝灌区抗旱能力概念及相应的计算模型。金菊良等[10]从水量平衡分析的角度构造区域抗旱能力系数，根据某一水平年、不同来水频率下的区域可供水量与需水量的比值，对区域抗旱能力进行定量评价。梁忠民等[13]基于相似的思想，定义了抗旱能力水平指数，反映抗旱能力大小。从水资源供需平衡分析的角度分析干旱应对能力，为定量评价提供一种思路，但用来水频率代替干旱频率的做法存在不足，因为来水频率一般是对应年时间尺度的，而干旱可能在一年内多次发生，或者跨年甚至是连年发生，这就存在干旱频率与来水频率不对应的现象。国外同类研究多从供水系统在干旱期的可靠性、适应性及恢复力的角度，对水利工程应对干旱的能力进行探讨[4, 14]，从评价方法上看，水利工程应对干旱能力多通过水库库容、水位在干旱期的变化情况来描述，且以定性分析为主，亦没有定量化的评价方法可供借鉴。

为此，在总结前人研究成果和不足的基础上，本文首先对水利工程群应对干旱的能力进行界定，从干旱的本质和干旱灾害形成机理出发，定义了干旱应对能力水平指数并详细介绍其计算方法，基于干旱应对能力水平指数评价区域水利工程体系应对干旱能力，较为系统地提出基于干旱时段水利工程群供水能力和水资源供需特征的定量评价方法。

1水利工程群应对干旱能力的定义

干旱应对能力研究尚处于起步阶段，目前还没有水利工程群应对干旱能力的确切定义。干旱的本质是缺水，水利工程应对干旱的能力在一定程度上可以理解成工程保障干旱期供水安全的能力。从干旱的一般定义出发，借鉴水库的防洪能力的定义[15]，将水利工程群应对干旱能力定义为：在某一具体的发展阶段，一定区域范围内的蓄、引、提、调等各类水利工程为保障正常的生产生活秩序在干旱期免受缺水影响，而具有的对某种程度干旱事件的调节能力。水利工程群应对干旱的能力应包括两层要义，一是要与作用对象的量级相对应，即对应一定的干旱频率(干旱重现期)；二是要强调最大程度的概念，即最大能有效应对多少年一遇的干旱。

2干旱应对能力水平指数

水利工程群应对干旱的本质是干旱期水利工程提供的水量能够满足用户多大程度的用水需求。因此，可将水利工程群应对干旱能力水平指数定义为：一定水平年，一定干旱频率下，干旱期水利工程的可供水量与需水量的比值，其表达式如下所示。

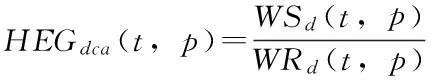
(1)

式中：HEGdca(t,p)为水利工程群(Hydrological Engineering Group,HEG)在水平年t、干旱频率p下的干旱应对能力(drought coping ability,dca)；WSd(t,p)为水平年t、干旱频率p下，干旱期间水利工程群调节下的供水能力；WRd(t,p)为水平年t、干旱频率p下，干旱期间保证正常的生产、生活所需水量，包括生产、生活和生态三部分的水量。水平年t主要反映不同水平年水利工程体系的数量、规模及布局情况的差异；干旱频率p则反映不同的干旱程度。

3干旱应对能力水平指数的计算

根据定义，计算干旱应对能力水平指数的关键是干旱期的确定以及干旱期需水量与可供水量的计算。

3.1干旱期的确定

干旱期与一次完整的干旱过程或干旱事件相对应。由于降水异常减少是引发干旱的根本原因，本文从气象干旱的角度，选取McKee等[16]在1993年提出的降水标准化指数(Standardized Precipitation Index,SPI)作为干旱诊断指标，识别流域干旱过程，并结合游程理论[17-18]进行干旱期的划分。

具体做法是以流域长系列月降水资料为基础，计算3个月时间尺度SPI，然后根据SPI干旱划分等级标准，以0为阈值，以±0.5为截断水平，认为当SPI小于0时可能发生干旱，从而可以划分出若干SPI<0的时段。假设两次SPI<0的时段之间仅间隔1个月且该月SPI值≥0但小于0.5，则认为两次干旱属于同一次干旱过程，否则若SPI值超出0.5，则认为两次干旱过程相互独立。对于某次干旱过程，持续时间仅有1个月且SPI≥-0.5(对应轻旱等级)，则认为小干旱过程(如图1中的b)，在本文中予以忽略。基于以上假设，在图1中共发生三次干旱过程，即包含三个干旱期(a，c和d)。以游程长度作为干旱持续时间D(即SPI值符合条件的月数)，游程总量作为干旱强度S(由SPI值累加得到，为了便于分析，取负变为正游程)，图中干旱期d的干旱持续时间D=d1+d2+1，相应的干旱强度S=S1+S2。

需要说明的是，在计算SPI时，之所以选择3个月时间尺度，是因为该尺度介于短尺度与长时间尺度之间，该尺度下的气候变异可显著引起土壤含水量的变化，对作物的生长演变产生重要影响，也是农业干旱风险分析中经常采用的时间尺度[19-21]。另外，阈值和截断水平的选取对干旱期划分也有一定的影响，需要结合流域历史干旱事件对相关参数进行合理性检验。

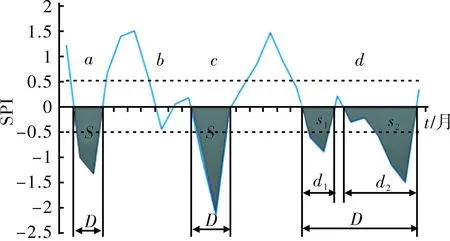
图1　基于游程理论的干旱特征定义

3.2干旱期需水量的计算

干旱期的需水量，需要综合考虑评价区域在干旱期间的降水情况、干旱程度、经济社会发展需求以及生态环境状况，确定各用水户的需水量。根据最新的《全国水资源综合规划技术细则》中的分类，用水户分为生活、生产和生态环境三大部分。生产需水主要考虑农业灌溉和工业生产两部分，生态环境需水包括河道内生态环境和河道外生态环境需水两部分。可根据用水定额与经济社会指标计算各部分需水量，再进行累加得到评价区域的总的需水量。其中，工业生产用水和生活用水计算相对简单，可采用定额法计算。农业需水量及需水过程的推求是重点。

对于充分灌溉条件下的农作物需水量，可以通过下式计算：

(2)

式中：Wirr是灌溉需水量(mm)；η是灌溉水利用该系数，是作物利用的灌溉水量与毛灌溉水量的比值；Kc是作物系数；Ep是潜在腾发量(mm)，可根据Penman-Monteith公式由气象资料推求；Pe是作物利用的有效降水量(mm)。

3.3干旱期可供水量的计算

可供水量的确定是计算HEGdca的关键，受到资料限制，实际中往往需要经计算获得。同时，由于水利工程群是由区域上蓄、引、提、调工程及闸坝工程组成的复杂供水系统，单独计算各类工程的供水能力不能反映区域工程体系整体的供水效益。因此，需构建面向干旱的水资源优化配置模型，采用长系列调算法确定每个干旱期内水利工程群的可供水量。同时，评价时段内一般存在多个干旱程度不同的干旱期，需要综合考虑每个干旱期的水资源供需过程，设定合理的整体调控目标，最终确定各干旱期的合理供水量。

3.3.1目标函数

设研究流域共有K个计算单元，计算单元k内有I(k)个供水水源、J(k)个用水部门。本文以一个优化周期内流域总缺水量最小为目标，设定如下目标函数：

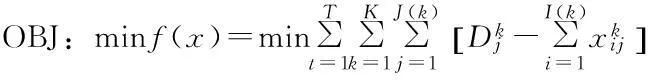
(3)

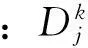
3.3.2约束方程

模型约束方程包括水量平衡方程和各类参数约束。

(1)计算单元水量平衡方程

Pzone_demand(i,t)=Cground*Xzone_ground_sup(i,t)+

Cres*Xres_sup(i,t)+Cpot*Xpot_sup(i,t)+

Cdiv*Xdiv_sup(i,t)+Xzone_lack(i,t)。

(4)

(2)水库单元水量平衡方程

Xres_end_cap(i,t+1)=Xres_end_cap(i,t)+Xpot_res(i,t)+

Xzone_res(i,t)-Xres_pot(i,t)-Xres_zone(i,t)-

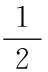
(5)

(3)节点水量平衡方程

Ppot_inflow(i,t)+Xres_pot(i,t)+Xpoti(i,t)+Xzone_pot

(i,t)=Xpot_res(i,t)+Xpoti_poti+1(i,t)+Xpot_zone(i,t)。

(6)

(4)水库库容约束方程

Pres_dead_cap(i,t)≤Xres_end_cap(i,t)≤

Pres_up_cap(i,t)。

(7)

式中：水库库容下限为死库容，汛期上限为防洪限制水位对应库容，非汛期上限为正常蓄水位对应库容。

(5)水库供水能力约束方程

Xres_zone(i,t)≤Pres_up_sup(i,t)。

(8)

(6)水库下泄流量约束方程

Priv_basic_flow(i,t)≤Xres_pot(i,t)≤Priv_max_flow(i,t)。

(9)

(7)引、提水工程供水能力约束方程

Xpot_zone(i,t)≤Ppot_up_sup(i,t)。

(10)

(8)地下水供水约束方程

Xzone_ground_cap(i,t+1)=Xzone_ground_cap(i,t)+

Pzone_ground_in(i,t)-Xzone_ground_sup(i,t)。

(11)

其中，

Pzone_ground_in(i,t)≤Pzone_ground_max(i,t)

(12)

(9)非负变量约束

对于以上任意变量，需满足非负条件，即∀X≥0。

上述约束方程中各参数、变量的含义统一列于表1，不再一一解释。

4水利工程群最大应对干旱能力的确定

确定干旱期需水量与可供水量以后，便可以计算水利工程群应对干旱能力水平指数HEGdca。当HEGdca=1时，供水量与需水量相等，完全不缺水；当HEGdca在(0, 1)区间变化时，HEGdca值越大，干旱期缺水率越小，水利工程群应对干旱能力越大。理论上，干旱期的可供水量随干旱程度的增大呈减小趋势，干旱期的需水量随干旱程度的增大而呈一定的增加趋势。计算一系列对应不同干旱程度的干旱应对能力水平指数，可以点绘成如图2所示的一条分段曲线。分段曲线的拐点也即水资源供需平衡的转折点，对应的干旱重现期记作TM，当发生重现期小于或等于TM的干旱事件时，可供水量大于需水量，实际供水量与需水量相等，可满足干旱期用水需求；当发生重现期大于TM的干旱事件时，可供水量小于需水量，并且缺水量随干旱程度的增大而增大。因此，TM可以认为是水利工程群所能应对的最大重现期的干旱。

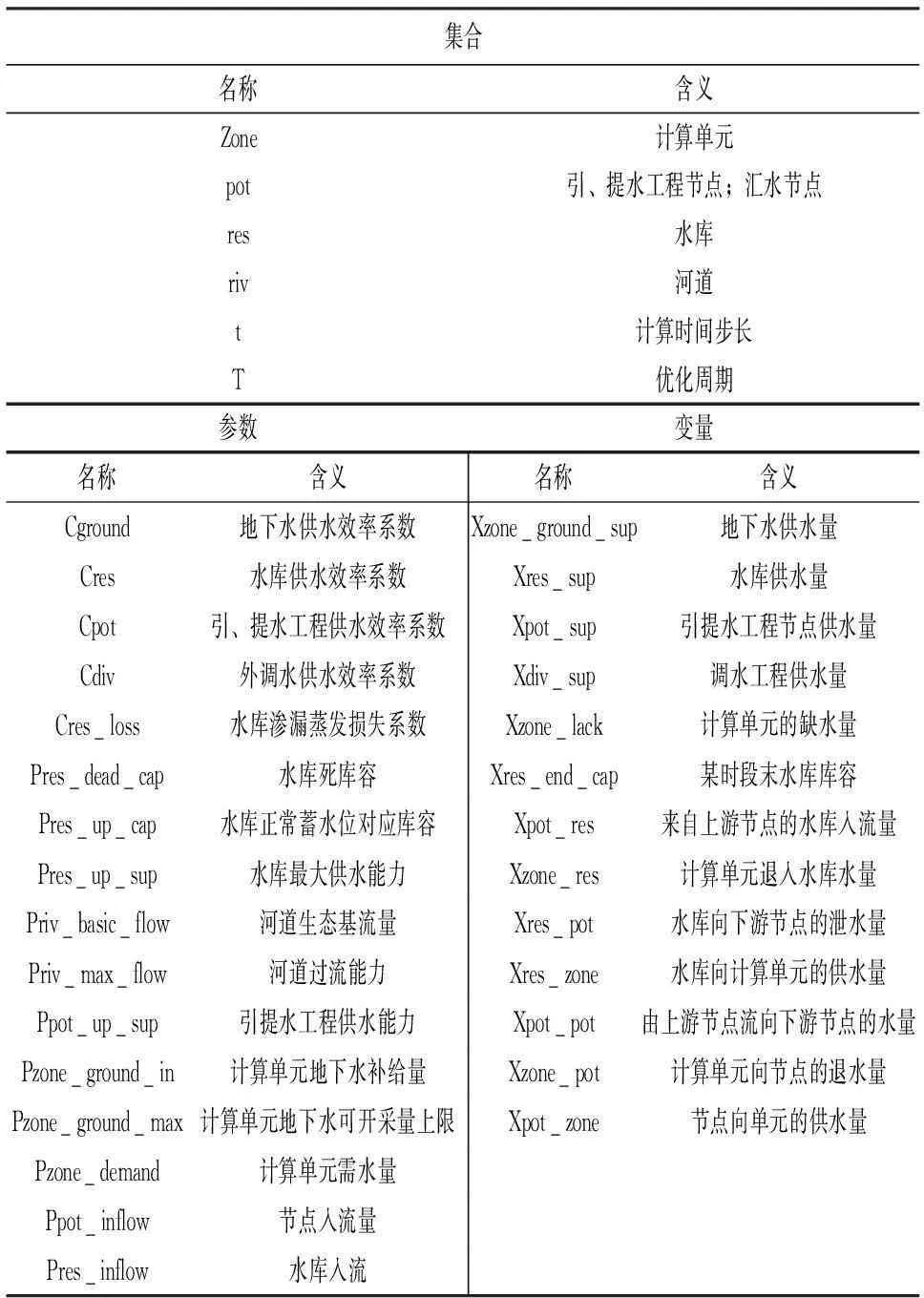
表1　模型系统集合、参数与变量名称及含义一览表

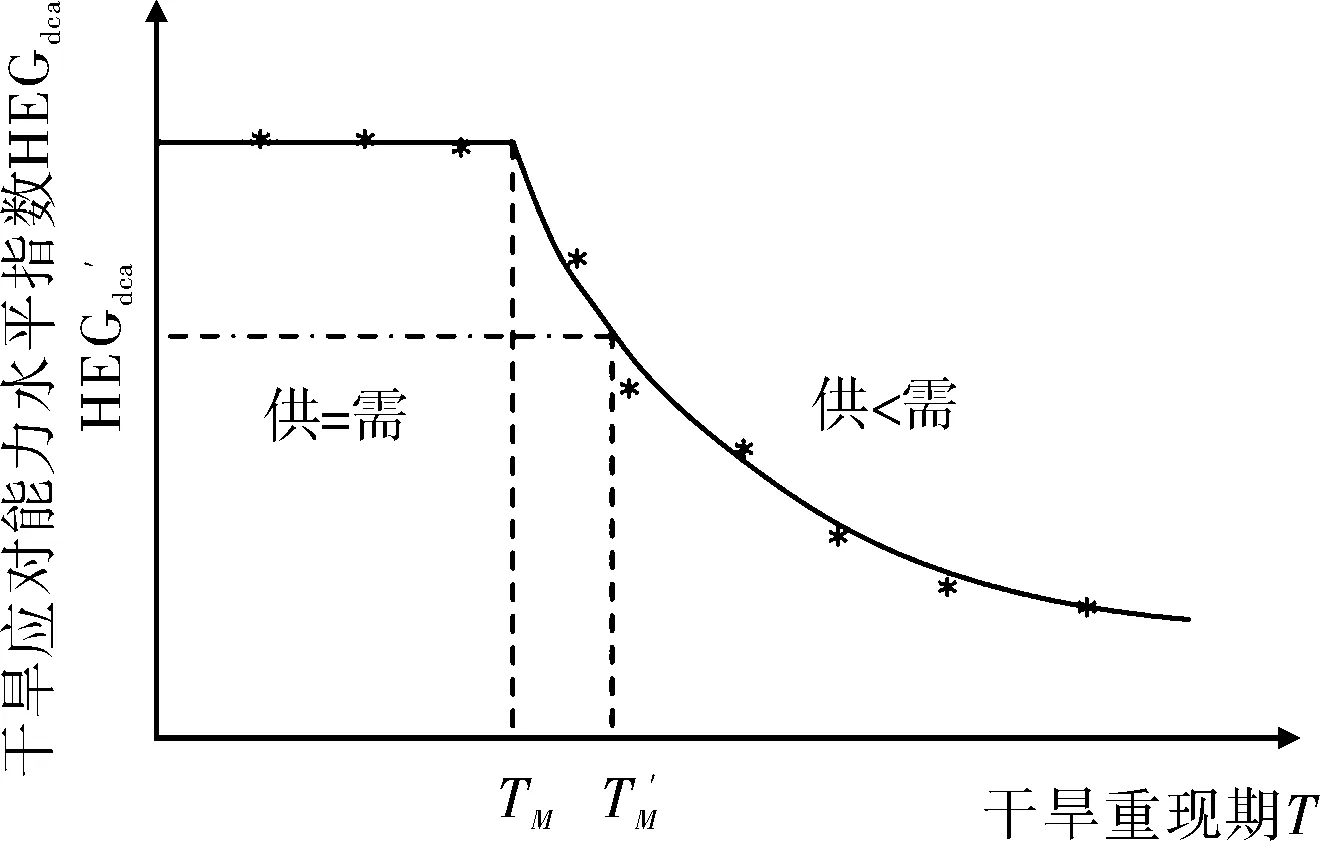
图2　干旱应对能力水平指数与干旱重现期的关系

对于水资源极度紧张的地区，干旱缺水会经常发生，绝对的供需平衡在实际中可能并不存在。因此，也可以在水资源供需平衡分析的基础上，以区域多年平均缺水率对应的干旱重现期TM作为工程体系可以应对的最大程度的干旱。假定区域多年平均缺水率为W缺，则与其对应的干旱应对能力水平指数HEGdca′=1-W缺。

基于以上分析，水利工程群最大应对干旱能力的确定除了计算干旱期工程可供水量与需水量以外，关键是确定每次干旱过程的重现期。干旱是一种包含多维特征变量的水文极值过程，各特征变量之间往往存在一定的相关性，单变量的分析难以准确描述干旱的特征。干旱历时和干旱强度是反映干旱程度大小的两个最重要的特征变量。因此，可以先分别拟合干旱历时和干旱强度的边缘分布，然后选取合适的Copula函数构造干旱历时与干旱强度的联合分布，并推求干旱联合分布的重现期。

5实例研究

5.1研究区概况

漳卫河流域位于海河流域南部，属于南运河水系的一部分，地理坐标为112.44°～115.34°E，35.01°～37.62°N，流域面积约3.53×104km2。漳卫河流域多年平均地表径流量为31.4×108m3，不重复地下水资源量15×108m3，水资源总量46.4×108m3。流域内有关河、后湾、漳泽、岳城、盘石头、小南海等6座大型水库，总库容27.13×108m3，中型水库25座，总库容8.03×108m3。引水工程665处，提水工程3 058处，引、提水工程的设计供水能力分别为26.97×108m3、11.84×108m3[22]。另外流域内有两处流域外(黄河)调水工程，分别通过人民胜利渠和共产主义渠引水，供漳卫河平原焦作和新乡两地，引水规模可达90 m3/s，现状供水能力为6.33×108m3。

漳卫河流域是我国最为缺水的地区之一，轻度及以上等级干旱发生的频次约为32.7%，且容易发生夏秋连旱和冬春连旱[23]。流域内有2万hm2以上的大型灌区6处，水资源开发利用程度较高，水资源综合开发利用率为81.8 %，地下水开发利用率达175 %，区域间竞争性用水矛盾突出，经济社会系统暴露性和脆弱性较大，研究区具有典型性。

5.2数据来源

本文计算SPI所使用的降水原始资料及用于计算彭曼公式所需的辐射、气温、水气压、风速等气象资料，均来自中国地面气象资料日值数据集，由中国气象局国家气象信息中心提供。本研究以漳卫河流域内各水资源三级区套地级市为评价单元，各单元有效灌溉面积来自于山西、河南、河北各省水利统计年鉴；各单元的工业、生活、生态用水数据参考了各省水利统计年鉴以及邯郸、安阳、新乡等相关地级市的水资源公报。构建水资源优化配置模型所需的各个计算单元的水资源量数据来源于全国第二次水资源综合规划成果，数据序列为1956-2000年。

5.3干旱期的划分及干旱频率的计算

5.3.1干旱期的划分及验证

基于漳卫河流域1957-2011年逐月降水资料，计算3个月时间尺度降水SPI指数。根据3.1节中基于游程理论的干旱特征的定义，统计干旱发生的次数，并计算相应的干旱历时及干旱强度，结果列于表2。漳卫河流域近55年来共发生了62次干旱过程，平均每年1.1次；干旱历时累计338个月，占统计总月数的51.2%；平均干旱历时5.5个月，平均干旱强度为4.2，干旱强度与干旱历时相关性较高，相关系数达到0.802。根据《海河流域水旱灾害》[24]记载，1949-1990年期间的典型旱灾年共有三次：1965年、1972年、1980-1982年。结合本文所确定的干旱期，1965年共发生两次干旱过程，分别是1月份开始的历时3个月的干旱和6月份开始的历时7个月的干旱，也即1965年的1-3月、6-12月均处在干旱期；1972年4月发生了一次历时7个月的干旱过程，即4-10月为干旱期；1980年8月至1981年7月发生一次持续12个月干旱过程，紧接着，从1981年10月开始又发生一次持续10个月的干旱过程，直至1982年7月，然后1982年11月再次发生一次持续5个月的干旱过程。历史记载的几次流域性大旱灾害均较好地得到了验证，因此，本文所述方法合理，确定的干旱期可用于后续的计算分析。

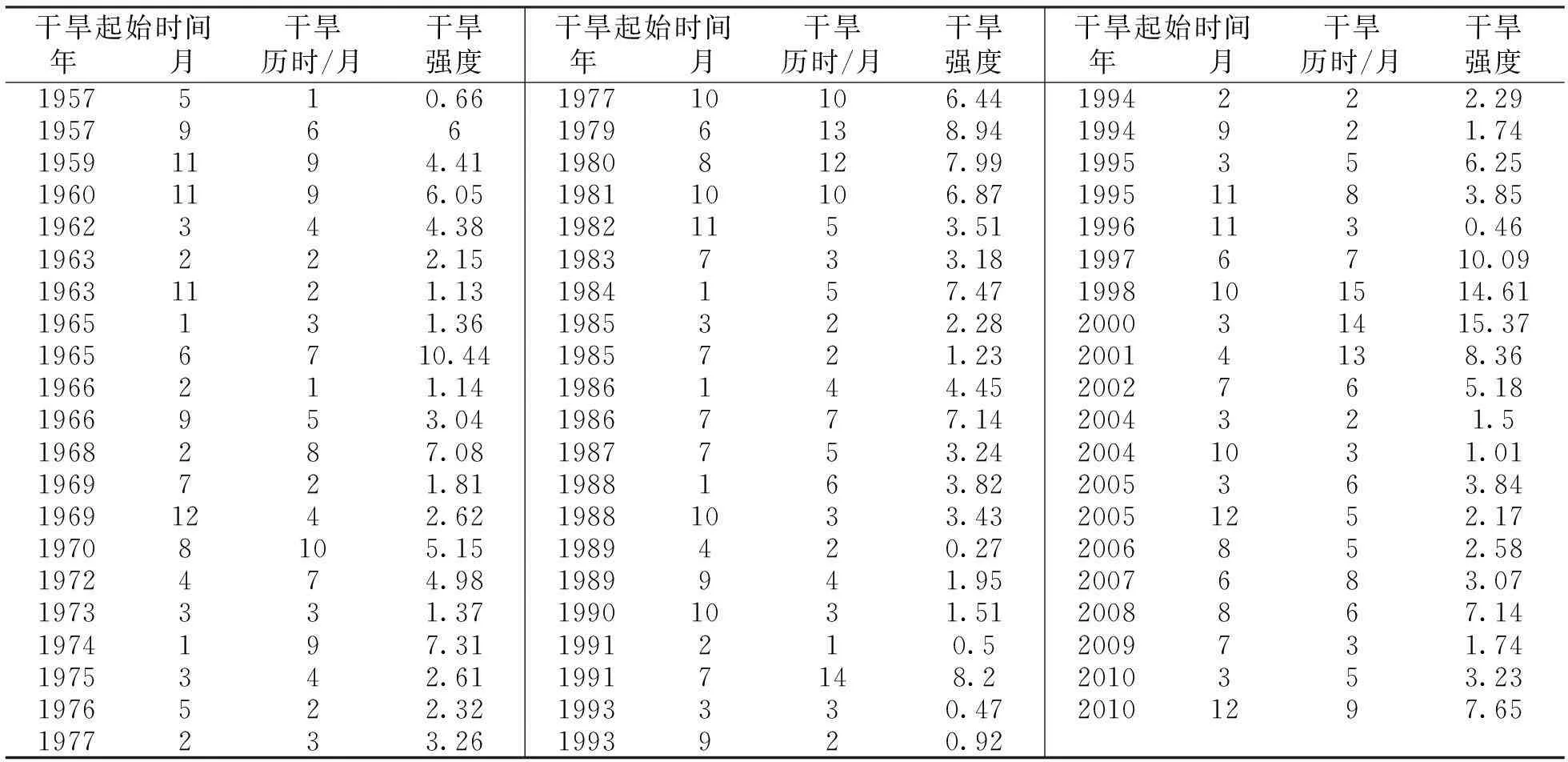
表2　漳卫河流域1957-2011年间历次干旱过程的历时及强度

5.3.2干旱频率计算分析

首先分别用指数分布和伽马分布拟合干旱历时和干旱强度的边缘分布，并用K-S方法对拟合分布进行检验。结果表明，在α=0.01的显著性水平上干旱历时和干旱强度分别服从指数分布和伽马分布。其次，选择三种应用最广泛的二维阿基米德型Copula函数：Gumbel-Hougaard、Clayton和Frank函数，分别建立干旱历时与干旱强度的联合分布，并根据均方根误差和纳什效率系数来检验拟合效果的优劣，同时考虑到Gumbel-Hougaard函数比较适合构造两变量间存在正相关关系的联结函数[25-26]，最终选用该种函数构建干旱历时与干旱强度的联合分布。根据Shiau[27]推导的计算公式得到干旱二重变量联合分布的重现期(受篇幅限制，表略)，并基于“D≥d且S≥s”类型的联合分布重现期进行干旱频率分析。由于用于供水计算的水资源量数据只到2000年，初步选取1970-2000年作为长系列调算的计算时段，该时段内既包含80～100年一遇的特大干旱过程(1979年6月、1980年8月、2000年3月等)，又包含若干次30～50年一遇的重度干旱过程(1977年10月、1986年7月等)和20～30年一遇的中等干旱过程(1974年1月、1981年10月等)，还有多次10～20年一遇及低于10年一遇的小干旱事件，基本能满足不同程度干旱期供需平衡分析的需要。

5.4干旱期需水量及可供水量的计算

5.4.1干旱期需水量及需水过程推求

分用户进行需水量的计算，重点是农业需水量和需水过程的推求，工业、生活和生态需水量做简化处理。

(1)农业需水量及需水过程

漳卫河流域旱地面积占耕地总面积的99.2%，作物种植结构稳定，主要为冬小麦-夏玉米种植模式，本文据此估算流域的作物需水量，重点考虑万亩以上灌区作物灌溉需水量。漳卫河上游山西地区与流域其他地区作物模式相同，但由于气候条件差异，作物生育期不大一致，并且考虑山区气候特点，夏玉米大多是在麦收前实施套种[28]，因此，需要分别计算流域上游山区和流域其它地区的作物需水过程。

本文先根据流域气象资料，采用彭曼公式求得潜在腾发量的月过程，可以得到理论上的充分灌溉条件下的作物灌溉需水量。但是各大型灌区都有较为完善的灌溉制度，直接采用理论计算结果可能与实际的灌溉水量会存在较大差异，因此，为了使评价结果对实际应用有更强的指导性，需要以理论需水过程为基础、结合实际灌水量进行必要的修正。由于实际灌溉需水量主要取决于作物需水量与有效降水量的差值，本文参考有关漳卫河流域大型灌区的研究成果[29]，一般年份每公顷耕地年净灌水量约2 430 m3，再结合典型年(75%频率)月降水过程，反推作物需水过程线。

对漳卫河流域1957-2011年面降水量进行排频计算，得到75%降水频率下的降水量为489.6 mm，对应的典型年有三个：1970年(490.2 mm)、1987年(487.2 mm)、2007年(489.6 mm)，选择降水分布最不利的年份1970年作为75 %频率典型年其降水过程及有效降水如图3所示，其中有效降水量由实际降水量乘以有效降水利用系数得到，相关系数选择参考文献[30]。通过反复推演，得到漳卫河平原区和上游山区冬小麦-夏玉米种植模式下作物需水月过程，分别如图4所示。

由作物需水月过程与长系列逐月有效降水过程，再结合每个计算单元的灌溉面积，就容易计算出净灌溉需水量。净灌溉需水量再除以灌溉水综合利用系数，可以得到农业灌溉总需水量。根据灌区试验资料，本文取灌溉水利用系数为0.517。

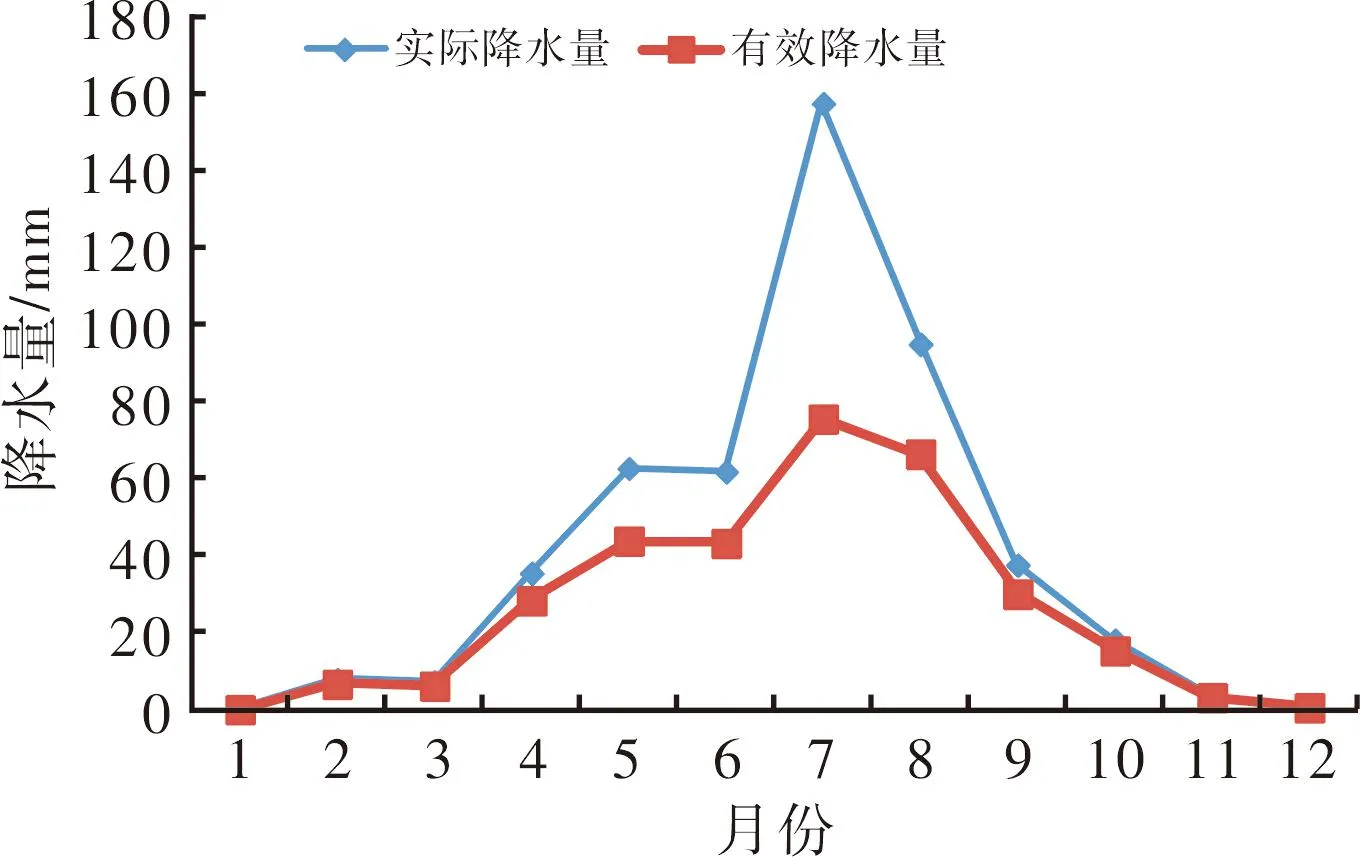
图3　漳卫河流域75%典型年降水与有效降水月过程

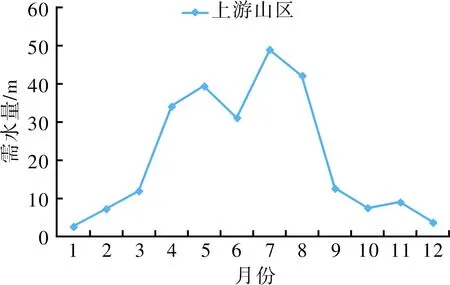
(a)上游山西地区

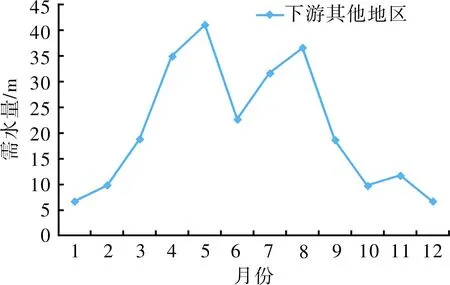
(b)流域其他地区 图4　漳卫河流域冬小麦-夏玉米种植模式作物需水量月过程

(2)工业和生活需水量

工业和生活需水量原则上用定额法予以确定。本文主要是评价一定水平年水利工程体系在不同干旱情景下的应对能力，以2010年为评价水平年，工业和生活需水量可统一用2010年的数据。考虑到工业和生活用水的供水保证率较高，严重的缺水破坏在实际中是不允许存在的，所以为简化起见，本文直接采用2010年的工业和生活实际用水量作为其需求量。同时，由于工业和生活用水过程较为平稳，将总需水量平均分配到每个月即可得到对应干旱期的工业、生活需水量。

(3) 生态需水量

本文的生态需水量包括河道内生态需水量和河道外生态需水量两部分。由于生态需水量占总需水的比例很小，不是需水计算考虑的重点，本文做简化处理。对于河道内生态需水，本文通过控制水库的下泄流量阈值来保证河道内生态需水，河道外生态环境需水用近5年实际生态环境用水量的平均值代替。

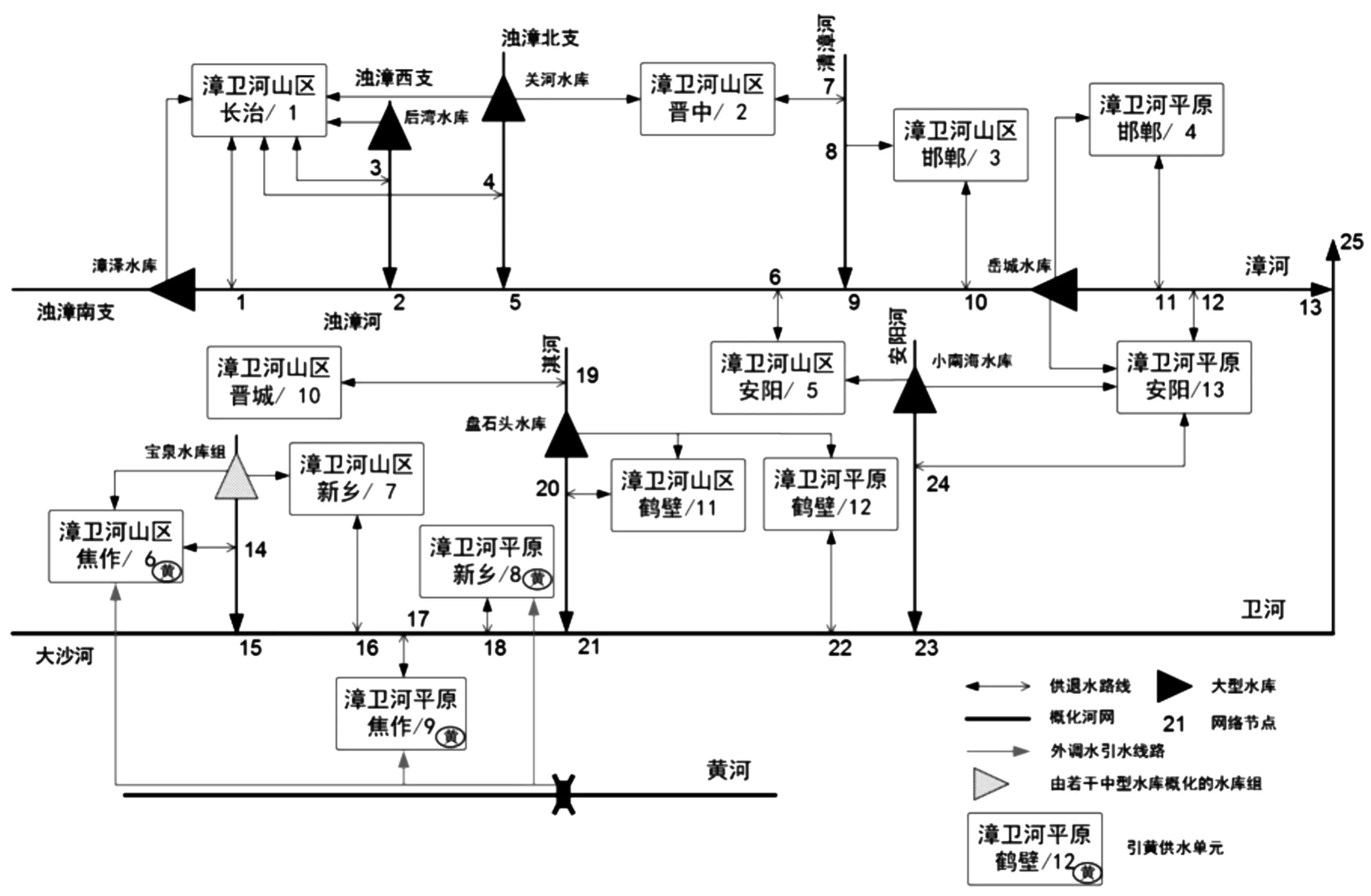
图5　漳卫河流域水资源系统拓扑图

5.4.2干旱期可供水量

首先以漳卫河流域的水系分布为基础，结合流域内行政单元划分和水利工程布局，将流域水资源系统概化为包括13个基本计算单元、25个配置节点、涵盖多种供水工程体系的网络结构(见图5)。以GAMS为基本的编程语言，构建漳卫河流域面向干旱的水资源优化配置模型，基于各计算单元长系列供需水数据，以月为时间步长，以年为优化周期进行动态调节计算。调用GAMS自带的软件包求解目标函数，计算干旱期可供水量。

基于第二次《海河流域水资源综合规划》成果[31]，先获取每个三级区套地级市评价单元的长系列年水资源量数据，然后根据代表水文站典型频率下的径流月过程，将各个评价单元年尺度上的水资源量分配到月上，再按模型要求的输入数据格式进行整理。经过模型调算得到各个评价单元1970-2000年系列逐月的可供水量。

5.5漳卫河流域水利工程群应对干旱能力评价结果及讨论

分别统计计算时段中各个评价单元历次干旱过程(干旱期)的可供水量及总需水量，并按流域将各评价单元供需水数据进行汇总，然后根据干旱期水资源供需关系计算整个流域及各评价单元的水利工程群应对干旱能力水平指数。现状水平年漳卫河流域1970-2000年间历次干旱过程的水量供需关系分析详细结果见表3，各评价单元的算表略。为了尽量克服采用数学分布函数进行干旱频率分析的不确定性和模型优化调算过程中的不确定性因素，将计算结果按对应的干旱程度大小分类汇总，取每组计算结果的平均值进行分析。

5.5.1流域整体应对干旱能力

由表3可知，漳卫河流域水利工程群应对小于10年一遇、10～20年一遇、20～30年一遇、30～50年一遇以及80～100年一遇干旱的能力水平指数分别为0.984 5、0.971 1、0.966 0、0.939 1、0.839 6。漳卫河流域为水资源极其紧张的地区，基于本文对水利工程群最大应对干旱能力的定义，并结合研究流域水资源禀赋及开发利用的实际情况，认为对于某个干旱过程，只要干旱期的缺水率不超过流域多年平均缺水率，那么水利工程群即成功应对了此次干旱事件。统计1970-2000年全年流域供需情况，可知流域多年平均缺水率为5.54 %，相对应的工程应对干旱能力指数为0.944 6，因此，漳卫河流域现状水利工程体系可以应对30年一遇以下的气象干旱，对于30～50年一遇的重度干旱尚不能有效应对，应对80～100年一遇的特大干旱事件能力较差，缺水率可达到15 %以上。

5.5.2各评价单元应对干旱能力对比

根据漳卫河流域各评价单元1970-2000年间历次干旱过程的水资源供需关系，得到如图6所示结果。以流域多年平均缺水率对应的工程应对干旱能力指数为阈值，评价各单元应对不同程度干旱的能力。

显然，对于小于10年一遇的干旱，所有评价单元现状工程条件都是可以应对的；对于10～20年一遇的干旱，除了漳卫河山区长治、山区晋中两个单元以外，其他单元也都是可以应对的；对于20～30年一遇的干旱，漳卫河山区长治、山区晋中、山区邯郸、山区晋城4个单元不能应对，而其他9个评价单元则可以有效应对；对于30～50年一遇严重干旱，则有漳卫河山区安阳、山区焦作、山区新乡、平原新乡、平原焦作、山区鹤壁、平原鹤壁、平原安阳等8个评价单元可以应对；而对于80～100年一遇特大干旱，流域内可以有效应对的单元只有山区焦作、山区新乡、平原新乡、平原焦作、平原鹤壁等5个评价单元。

5.5.3结果合理性分析

按照各个评价单元最大的干旱应对能力绘制漳卫河流域水利工程群干旱应对能力空间对比图，如图7所示。水利工程群干旱应对能力定量评价的结果与文献[32]中基于多指标的综合评价结果基本一致。漳卫河山区安阳、山区新乡、平原新乡、平原焦作、平原鹤壁、平原安阳等6个评价单元的综合评价结果为“较强”，而根据定量评价结果，它们均能够应对30～50年一遇甚至80～100年一遇的干旱；漳卫河山区长治、山区晋中的综合评价结果为“弱”，而定量评价结果为仅能应对小于10年一遇的干旱。只有漳卫河山区焦作、平原邯郸的定量与定性评价结果不大一致。漳卫河流域整体可以应对30年一遇以下的干旱与综合评价等级为“中等”相符。两种方法评价结果可以相互印证，这从侧面反映了本文提出的水利工程群应对干旱能力定量评价方法合理，评价结果可以为流域干旱管理实践提供借鉴。

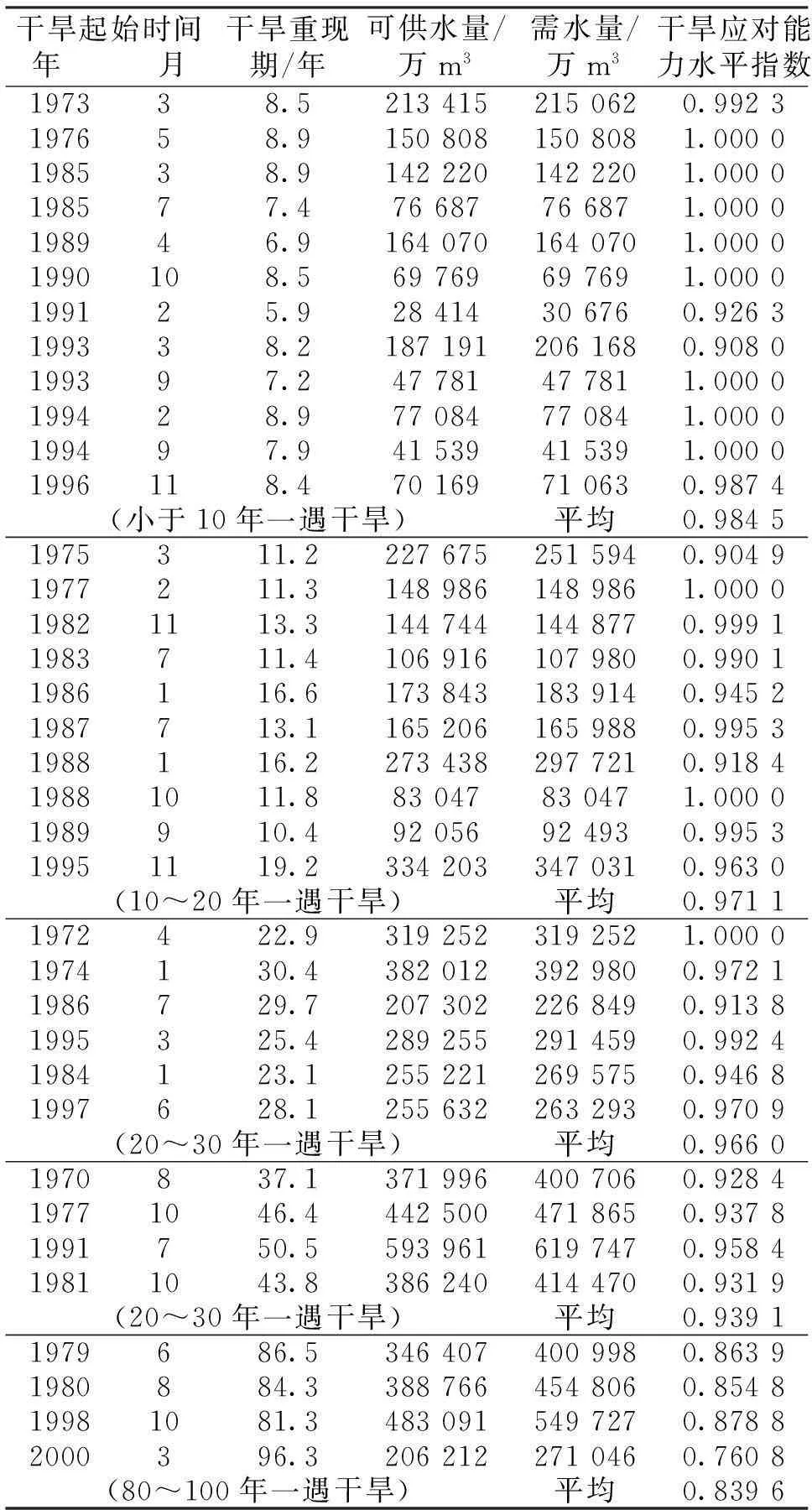
表3　现状水平年漳卫河流域1970-2000年间历次

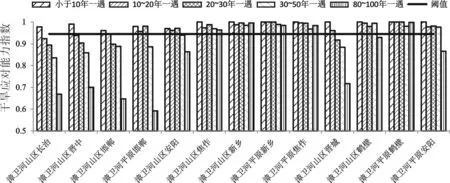
图6　现状年漳卫河流域各评价单元应对不同程度干旱能力对比

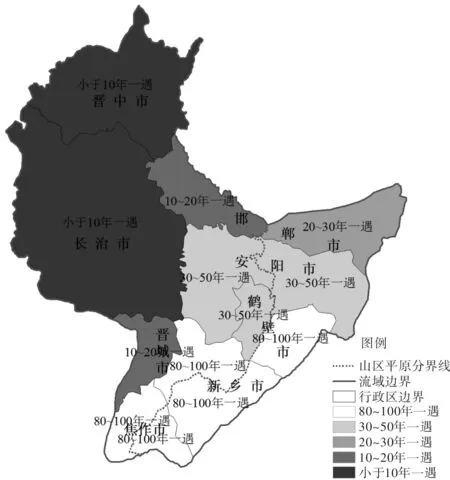
图7　现状年漳卫河流域各评价单元应对干旱能力对比

6结论

水利工程群应对干旱能力评价与调控研究是应对极端水文水资源事件的核心内容之一，也是流域抗旱规划和干旱风险管理的重要基础性工作之一。本文以流域水资源系统为研究对象，以干旱时段水利工程群的供水能力和水资源供需特征为着力点，定义了水利工程群应对干旱能力水平指数(HEGdca)。基于游程理论定义干旱特征并采用比较成熟的多维联合分布理论进行干旱频率计算，以解决采用典型干旱年的来水频率代替干旱频率的不足。通过不同干旱程度下的HEGdca与干旱频率之间的对应关系以及它们所反映出的水资源供需平衡的变化，对水利工程群最大应对干旱能力进行定量表达。该方法物理意义明确，计算过程简便，可为客观评价区域水利工程体系应对干旱的能力、制定防旱抗旱规划提供技术支撑。

以漳卫河流域为例，开展水利工程群应对干旱能力定量评价实证研究。漳卫河流域水利工程群应对小于10年一遇、10～20年一遇、20～30年一遇、30～50年一遇以及80～100年一遇干旱的能力水平指数分别为0.984 5、0.971 1、0.966 0、0.939 1、0.839 6。以流域多年平均缺水率为衡量标准，漳卫河流域现状水利工程体系(2010水平年)整体可以应对30年一遇以下的气象干旱事件，对于30～50年一遇的重度干旱以及80～100年一遇的特大干旱事件则不能有效应对。在流域13个评价单元中，有8个单元可以应对30～50年一遇及以上干旱，其中5个评价单元可以应对80～100年一遇干旱；其余5个评价单元中，能够应对20～30年一遇的评价单元有1个，能够应对10～20年一遇和10年一遇以下干旱的评价单元分别有2个。总体而言，漳卫河上游山区应对干旱能力较弱，卫河流域应对干旱能力强于漳河流域，这与流域内大型灌区分布、当前流域外调水工程供水范围有关。定量评价结果与综合评价结果比较一致，且基本能反映流域的实际情况，可以为流域抗旱规划和干旱风险管理提供支撑。

本文研究还存在一些不足，比如在需水量计算中，重点关注农业，而未考虑工业、生活用水及生态系统用水在不同干旱情景下可能发生的变化；相关模型还需进一步完善；未涉及水质对供水的影响等。

参考文献:

[1]程晓陶. 加强水旱灾害管理的战略需求与治水方略的探讨[J]. 水利学报, 2008, 39(10): 1197-1203.

[2]亚行技援中国干旱管理战略研究课题组. 中国干旱灾害风险管理战略研究[M]. 北京: 中国水利水电出版社, 2011.

[3]杨敏, 毕志国. 浅谈六盘水市水利工程在2010年大旱中发挥的作用[J]. 中国水利, 2010(14): 42-43.

[4]Watts G, Von Christierson B, Hannaford J, et al. Testing the resilience of water supply systems to long droughts[J]. Journal of Hydrology, 2012(414/415): 255-267.

[5]Wang G, Yan D H, Yang Z Y, et al. drought-coping capacity assessment of water resources projects and regulation: A technological framework and key issues for research[J]. Advanced Materials Research, 2014, 864: 2268-2277.

[6]费振宇, 周玉良, 金菊良, 等. 区域抗旱能力评价指标体系和评价模型的构建[J]. 灾害学, 2013, 28(4): 197-204.

[7]顾颖, 张东, 郦建强, 等. 区域抗旱能力评价技术开发与应用[J]. 水利水电技术, 2014, 45(4): 145-148.

[8]康蕾, 张红旗. 中国五大粮食主产区农业抗旱能力综合评价[J]. 资源科学, 2014, 36(3): 481-489.

[9]王刚, 严登华, 吴楠, 等. 水利工程群应对干旱能力评价方法及应用[J]. 灾害学, 2015,30(1)：39-44.

[10]金菊良, 费振宇, 郦建强, 等. 基于不同来水频率水量供需平衡分析的区域抗旱能力评价方法[J]. 水利学报, 2013, 44(6): 687-693.

[11]屈艳萍, 郦建强, 吕娟, 等. 旱灾风险定量评估总体框架及其关键技术[J]. 水科学进展, 2014, 25(2): 297-304.

[12]金菊良, 原晨阳, 蒋尚明, 等. 基于水量供需平衡分析的江淮丘陵区塘坝灌区抗旱能力评价[J]. 水利学报, 2013, 44(5): 534-541.

[13]梁忠民, 郦建强, 常文娟, 等. 抗旱能力研究理论框架[J]. 南水北调与水利科技, 2013, 11(1): 13-18.

[14]Lee S, Abdul-Talib S, Park H. Lessons from water scarcity of the 2008-2009 Gwangdong reservoir: needs to address drought management with the adaptiveness concept[J]. Aquatic Sciences, 2012, 74: 213-227.

[15]叶守泽. 水文水利计算[M]. 北京: 水利水电出版社, 1992.

[16]McKee T B, Doesken N J, Kleist J. The relationship of drought frequency and duration to time scales[C]//Preprints, Eighth Conference on Applied Climatology. Anaheim: American Meteorological Society,1993:174-184.

[17]Yevjevich V. An objective approach to definitions and investigations of continental hydrologic droughts[M]. Fort Collins: Colorado State University, 1967.

[18]Dracup J A, Lee K S, Paulson E G. On the definition of droughts[J]. Water Resources Research, 1980, 16(2): 297-302.

[19]Rouault M, Richard Y. Intensity and spatial extent of droughts in southern Africa[J]. Geophysical Research Letters, 2005, 32(15).

[21]Moreira E E, Coelho C A, Paulo A A, et al. SPI-based drought category prediction using loglinear models[J]. Journal of Hydrology, 2008, 354(1): 116-130.

[22]田术存. 漳卫南运河水资源合理配置研究[D]. 南京: 河海大学, 2007: 22-24.

[23]王刚, 严登华, 申丽霞, 等. 近55年以来漳卫河流域干旱演变特征分析[J]. 南水北调与水利科技, 2014, 12(4): 1-5.

[24]水利部海河水利委员会. 海河流域水旱灾害[M]. 天津: 天津科学技术出版社, 2009.

[25]陆桂华, 闫桂霞, 吴志勇, 等. 基于copula函数的区域干旱分析方法[J]. 水科学进展, 2010, 21(2): 188-193.

[26]Mirabbasi R, Fakheri-Fard A, Dinpashoh Y. Bivariate drought frequency analysis using the copula method[J]. Theoretical and Applied Climatology, 2012, 108(1/2): 191-206.

[27]Shiau J T. Fitting drought duration and severity with two-dimensional copulas[J]. Water Resources Management, 2006, 20(5): 795-815.

[28]孙景生, 康绍忠, 张寄阳, 等. 霍泉灌区冬小麦夏玉米高产节水灌溉制度[J]. 农业工程学报, 2000, 16(4): 50-53.

[29]水利部海委漳河上游管理局. 漳卫河上游年度水量调度方案编制与实施[R]. 邯郸：水利部海委漳河上游管理局，2012.

[30]严登华, 袁喆, 杨志勇, 等. 1961 年以来海河流域干旱时空变化特征分析[J]. 水科学进展, 2013, 24(1): 34-41.

[31]水利部海河水利委员会. 海河流域水资源综合规划[R]. 天津：水利部海河水利委员会，2008.

[32]王刚. 水利工程群应对干旱能力评价及调控研究——以漳卫河流域为例[D]. 北京: 中国水利水电科学研究院, 2014: 78-86.

裴欢，王晓妍，房世峰. 基于DEA的中国农业旱灾脆弱性评价及时空演变分析[J].灾害学, 2015,30(2):64-69. [Pei Huan, Wang Xiaoyan and Fang Shifeng. Study on temporal-spatial evolution of agricultural drought vulnerability of China based on DEA model[J].Journal of Catastrophology, 2015,30(2)：64-69.]

Study on Drought Coping Ability Assessment of Hydraulic EngineeringProjects：Quantitative Evaluation Method and a Case Study on Zhangwei River Basin

Wang Gang1, 2, Pan Tao1, Yan Denghua3, Qi Jun1, Liu Shaohua3, Zhao Ji-wei4

(1.BeijingMunicipalResearchInstituteofEnvironmentalProtection,Beijing100037,China; 2.College

ofEnvironmentalScienceandEngineering,DonghuaUniversity,Shanghai201620,China;

3.WaterResourcesDepartment,ChinaInstituteofWaterResourcesandHydropowerResearch,Beijing

100038,China; 4.SchoolofWaterConservancyEngineering,NorthChinaUniversityofWaterResources

andElectricPower,Zhengzhou450045,China)

Abstract:Hydraulic engineering group refers to a complex water supply system, consisting of water conservancy projects, water diversion projects, water lifting projects, inter-basin water transfer projects as well as sluice and dam projects. It has been accepted to be a key support to deal with regional droughts. Given that the expression of drought coping ability is not uniform and the current quantitative evaluation methods need to be improved, the connotation of drought coping ability of hydraulic engineering projects has been defined firstly. Then the drought coping ability index of hydraulic engineering group (HEGdca) was defined from the perspective of both essence of drought and the forming mechanism of drought disaster. Finally, a quantitative evaluation method of drought coping ability of hydraulic engineering projects has been put forward based on the HEGdca. Taking 2010 as the level year for evaluation, the HEGdcaunder given project condition has been calculated for different drought scenarios in the study area. The result shows that when taking the average water deficient ratio as the criteria for evaluation, the current (2010) hydraulic engineering projects in the Zhangwei River basin can effectively resist a meteorological drought event with less than 30-year return period on the whole. The result of quantitative evaluation is generally consistent with the actual situation of the study area, which can offer a technological support for drought planning and the risk management of drought disaster.

Key words:hydraulic engineering projects; drought coping ability index; quantitative evaluation; run theory; water resources optimal allocation model; Zhangwei River basin

doi:10.3969/j.issn.1000-811X.2015.02.011

中图分类号：X4

文献标志码：A

文章编号：1000-811X(2015)02-0056-08

作者简介：王刚(1985-)，男，河南平顶山人，博士，主要从事气候变化下水资源综合应对研究. E-mail: Gangwnan@163.com通讯作者：严登华(1976-)，男，安徽太湖人，博士，教授级高工，主要从事气候变化下水资源综合应对、生态水文学及地理信息技术应用等研究. E-mail: yandh@iwhr.com

基金项目：国家重点基础研究发展计划(973计划)项目“气候变化对黄淮海地区水循环的影响机理和水资源安全评估”(2010CB951102)；国家自然科学基金面上项目“基于水资源系统的广义干旱风险评价与风险区划研究”(51279207)

收稿日期：2014-09-01修回日期：2014-10-22