三维空间下的证据权建模方法与资源预测应用

潘诗辰， 毛先成

(1.中南大学有色金属成矿预测教育部重点实验室，湖南长沙410083； 2.中南大学地球科学与信息物理学院，湖南长沙410083)

三维空间下的证据权建模方法与资源预测应用

潘诗辰1,2， 毛先成1,2

(1.中南大学有色金属成矿预测教育部重点实验室，湖南长沙410083； 2.中南大学地球科学与信息物理学院，湖南长沙410083)

摘要：为了探索证据权法在三维空间下成矿预测的实际应用，在传统证据权的基础上，探讨了适用于三维空间下成矿预测的证据权建模思路和方法。并以Visual Studio 2010为开发平台，在Access 2003中建立多元地学空间数据库，开发可进行证据因子选择、因子权重计算及后验概率计算的证据权软件WofE3DSys，其输出结果可在Voxler中进行三维可视化呈现。经分析，WofE3DSys计算结果与Arc-WofE输出结果在异常圈定方面基本一致，验证了WofE3DSys的准确性。最后，以招平断裂带大尹格庄金矿为实例，选取成矿信息作为证据图层，进行成矿预测。该研究是对三维空间下证据权法的一次探索，为将来该证据权法在其他矿区的成矿预测提供了现实依据。

关键词：三维建模；证据权法；后验概率；成矿预测；山东

doi:10.3969/j.issn.1674-3636.2015.03.373

中图分类号：P628

文献标识码：A

文章编号：1674-3636(2015)03-0373-10

收稿日期：2015-06-12；修回日期：2015-06-19；编辑：陆李萍

基金项目：国家自然科学基金项目(41472301，41172297)，国家“十二五”科技支撑计划项目(2011BAB04B10)

作者简介：潘诗辰(1992—)，女，硕士研究生，研究方向为GIS、地学三维建模和隐伏矿三维预测，E-mail: shichenpan@126.com

0引言

矿产资源预测方法有回归分析法、判别分析法、聚类分析法、证据权重法等。证据权法以贝叶斯条件概率为基础，通过将多个成矿信息的二值图像进行叠加得到后验概率来圈定成矿有利区。每一种成矿信息都作为1个证据因子，每一个证据因子对成矿预测的贡献程度由其权重值决定。证据权法自提出以来，已在矿产资源潜力评价中获得广泛应用，国内外均有许多应用实例(胡光道等，1998；肖克炎等，1999；丁清峰等，2006；李卫东等，2009；胡官兵等，2010；赵增玉等，2010；刘岳等，2011；张宝一等，2012；Harris et al，2000；Asadi et al，2001；Chen，2004；Porwal et al，2010)。针对证据权法中存在的二值化信息损失和条件独立性检验问题，有学者提出了模糊证据权法、加权证据权和A-C检验模型等改进模型(张生元等，2009；Cheng et al，1999；Agterberg et al，2002；Jounel，2002；Cheng，2008)。

传统的成矿预测方法已随着三维地质建模、三维空间分析等三维地质技术的飞速发展进入新的阶段。国内外已有许多学者对三维空间下的资源预测评价方法开展了研究，如赵鹏大等(1992)运用统计分析方法建立矿床值与控矿因素之间定量联系的三维空间定位预测模型；Fallara等(2006)研究三维地质集成建模方法并应用于加拿大Joutel VMS矿床和Duparquet金矿的矿床勘探；毛先成(2006)通过三维成矿信息定量提取开展隐伏矿体立体定量预测；陈建平等(2007)采用三维可视化技术和信息量法开展隐伏矿体三维预测；Wang等(2011)利用神经网络和分形方法对国内栾川矿区进行三维成矿预测；肖克炎等(2012)通过立方体预测模型的建立进行三维矿产预测与资源评估。由传统中小比例尺的区域成矿远景区预测转为大比例尺的矿区深边部立体预测，成为近年来找矿工作的主要趋势之一。

以往利用证据权法进行成矿预测往往基于中小比例尺的二维地表展开研究，并以矿区作为预测对象。因此，本次研究将传统二维证据权的建模方法改进为适用于三维空间下隐伏矿体立体预测的建模方法，并分别探讨了普通证据权和模糊证据权法建模的思路和方法。以Visual Studio 2010为开发平台，在Access 2003中建立多元地学空间数据库，开发可进行证据因子选择、因子权重计算及后验概率计算的证据权软件WofE3DSys。经分析，WofE3DSys计算结果与Arc-WofE输出结果在异常圈定方面基本一致，验证了WofE3DSys的准确性。最后以招平断裂带大尹格庄金矿为实例，选取成矿信息作为证据图层，进行成矿预测。实现了对三维空间下证据权法的一次探索，为将来该证据权法在其他矿区的成矿预测提供了现实依据。

1建模方法

1.1　证据权重法原理

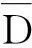
每个证据层拥有正、负权值W+和W-。W+、W-分别为证据因子存在单元和不存在单元的权重值，数据缺失单元权重值为0。正、负权值之差C值(C=W+-W-)表示证据层与矿(床)点的相关程度，若C=0，表示该因子对矿(床)点出现与否无指导意义；若C>0，表示该因子有利于成矿；若C<0，表示该因子不利于成矿。一般采用最大C值(刘世翔等，2007)或标准C值(Asadi et al，2001)来确定最优切值。

(1)

式(1)中，

(2)

任一单元格的后验概率表示该单元含矿的概率大小。计算后验概率前，各证据因子间需要相对于矿点分布满足条件独立。对于n个证据因子，研究区任一单元k为矿点的可能性(后验几率O后验)的对数表示：

(j=1,2,3,…,n)

(3)

式(2)中，O(D)为先验优劣比，即：

(4)

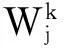
(5)

最后得到后验概率P为：

(6)

1.2　基于普通证据权的建模方法

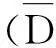
图1　研究区单元格划分图Fig.1　Cell division in the study area

图2　矿化信息图层二值化示意图Fig.2　Sketch showing layer binarization of mineralization layer

表1　普通证据权法数据库表结构

1.3　基于模糊证据权的建模方法

模糊证据权法单元划分方法与普通证据权法相同。划分出的每个立方体均拥有含矿信息和成矿信息，将这些数据储存在Microsoft Access 2003中(表2)。

表2　模糊证据权法数据库表结构

普通证据权法是将证据因子二值化，证据图层只含有证据因子“存在”与“不存在”2种状态，对于连续数据会存在信息损失的问题。针对这一问题，有学者提出了“模糊证据权法”(Cheng et al，1999)，通过用“模糊度”概念来定量确定多分类证据因子对成矿的相关程度。“模糊度”则通过隶属度(0≤μA(x)≤1)来确定，使证据图层成为一个模糊集合，而不是简单的二值分类。

假设共有n个证据因子，先将证据因子Aj(j=1,2,3,…,n)的属性值分为mj个区间类，体元k的后验概率计算如下。

计算正、负权重值及差值C。根据式(1)计算证据因子Aj每个属性类的正、负权重值和差值C。

计算隶属度。设Aj1和Aj2(Aj1∪Aj2⊂T,Aj1∩Aj2=0)的定义如下：

Aj1={x|μjt(x)=1},Aj2={x|μjt(x)=0}

(j=1,2,3,…,n;t=1,2,…,mj)

(7)

式(7)中，隶属度μjt根据如下线性关系计算：

(j=1,2,3,…,n;t=1,2,…,mj)

(8)

(j=1,2,3,…,n;t=1,2,3,…m)

(9)

后验概率计算。对于n个证据因子，研究区任一体元k为含矿单元的可能性优劣比的对数表示：

k=1,2,3,…,T)

(10)

式(10)中，O(D)为D的先验优劣比，即：

(11)

最后得到单元k的后验概率P为：

(12)

2软件设计与开发

2.1　WofE3DSys软件模块

证据权法软件WofE3DSys由2个模块构成：普通证据权法和模糊证据权法。普通证据权法与模糊证据权法模块(图3、图4)计算流程类似(图5)：(1) 输入样本数据库，选择含矿指标；(2) 在证据因子选择框中选择要参与计算的证据因子，模糊证据权则还需输入各证据因子的区间个数；(3) 进行权重计算，计算结果可以导出为文本文件；(4) 最后输入预测数据库，进行后验概率计算。

图3　普通证据权法模块界面Fig.3　Module interface of the common weights of evidence modeling

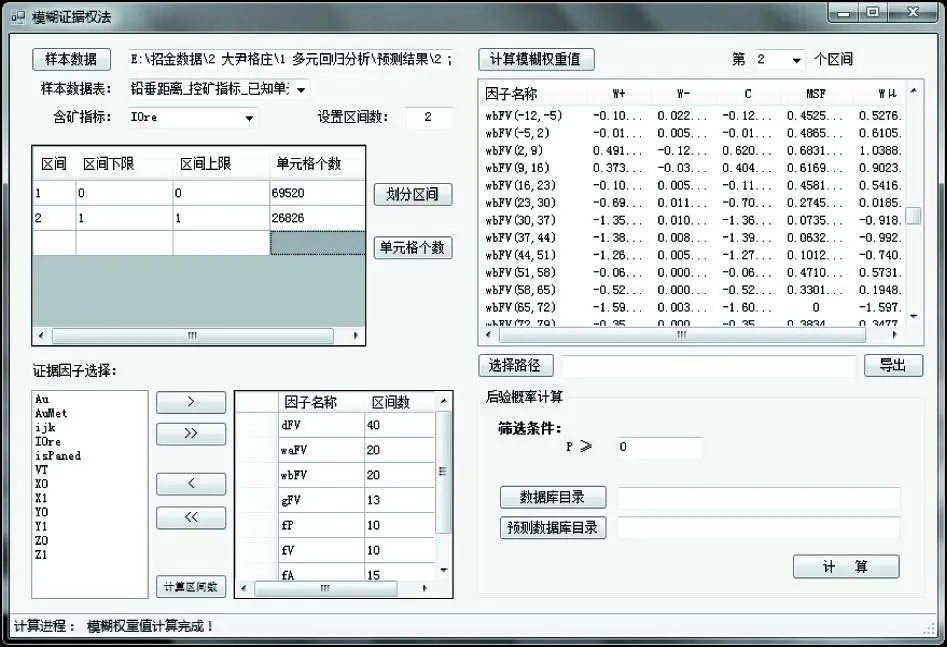
图4　模糊证据权法模块界面Fig.4　Module interface of the fuzzy weights of evidence modeling

图5　证据权法程序流程图Fig.5　Flow chart showing procedure of the weights of evidence modeling

2.2　WofE3DSys软件结果准确性分析

ArcGIS软件中含有证据权法的扩展模块Arc-WofE。通过利用Arc-WofE模块进行成矿预测，将预测结果与WofE3DSys软件计算所得结果进行比较，分析WofE3DSys的准确性。选取招平断裂带中段及其周围区域为研究对象，研究区内存在15个已知矿点，单元划分精度为50 m×50 m，证据因子为单元格到主断裂的最短距离、单元格投影到主断裂点走向、单元格投影到主断裂点破碎带宽度3个因子(图6)。从图6可以看出，采用Arc-WofE计算得到的招平断裂区域金矿预测后验概率的异常划分与采用WofE3DSys软件得到的异常划分结果一致。假定图6中的6级分区按概率从高到底标记为1—6级异常区，则(a)、(b)图中15个已知矿点中均有11个点落在1、2级异常区中。因此相对于Arc-WofE扩展模块的异常划分结果而言，WofE3DSys软件所得结果是准确的。

图6　采用2种途径的普通证据权成矿预测后验概率图(a) 基于Arc-WofE的普通证据权；(b) 基于WofE3DSys软件的普通证据权Fig.6　Posterior probability maps for metallogenic prediction using two ways of the common weights of evidence modeling(a) common weights of evidence modeling based on Arc-WofE; (b) common weights of evidence modeling based on WofE3DSys software

普通证据权法和模糊证据权法计算得到的后验概率图分别见图7的(a)和(b)。将2种方法的后验概率结果统一分成5类区间：后验概率值范围第1类为0.001 000～0.005 000,第2类为0.000 300～0.001 000,第3类为0.000 100～0.000 300,第4类为0.000 050～0.000 100,第5类为0～0.000 050，统计落入每个区间内的已知矿点个数，由此得到后验概率结果分类区间与累积矿点对比曲线图(图8)。图中当后验概率分类为第1类时，由于模糊证据权法计算得到的后验概率最高值较普通证据权法高，因此普通证据权法没有已知矿点落在该区间，累积矿点数为0，而模糊证据权法有5个已知矿点落入该区间，累积矿点数为5；当后验概率分类为第5类时，2种方法的所有已知矿点均落入5个分类区间内，故2种方法的第5类区间累积矿点数相等，均为15。并且因2种方法计算结果均为高后验概率区间包含的已知矿点数高于低概率区间，所以图中曲线表现为高概率区2种方法的差异大于低概率区，即2条曲线的差异呈减小趋势。由图可知在同一后验概率区间，模糊证据权法计算得到的累积矿点数比普通证据权法高，这表示对于同一高概率值范围，模糊证据权法比普通证据权法包含更多的已知矿点，且在相同累积矿点数的情况下，模糊证据权法的后验概率较高。因此，模糊证据权法的准确性较普通证据权法高。

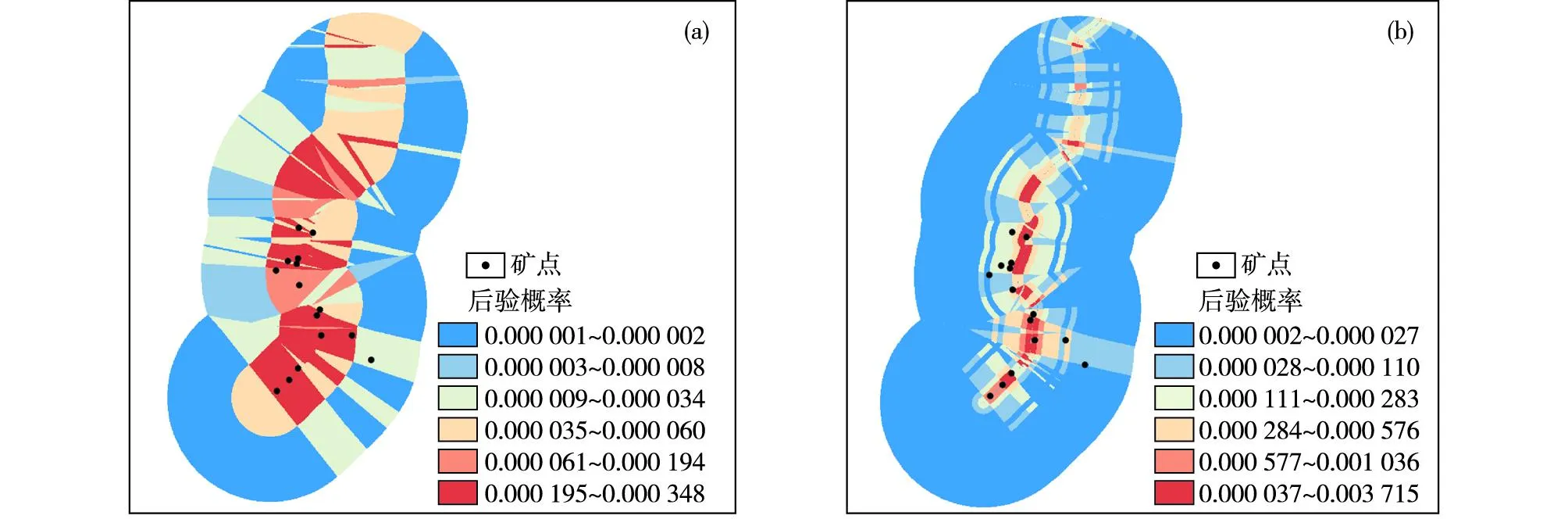
图7　普通证据权和模糊证据权成矿预测后验概率图(a) 基于WofE3DSys软件的普通证据权；(b) 基于WofE3DSys软件的模糊证据权Fig.7　Posterior probability maps for metallogenic prediction by the common and fuzzy weights of evidence modeling(a) common weights of evidence modeling based on WofE3DSys software; (b) fuzzy weights of evidence modeling based on WofE3DSys software

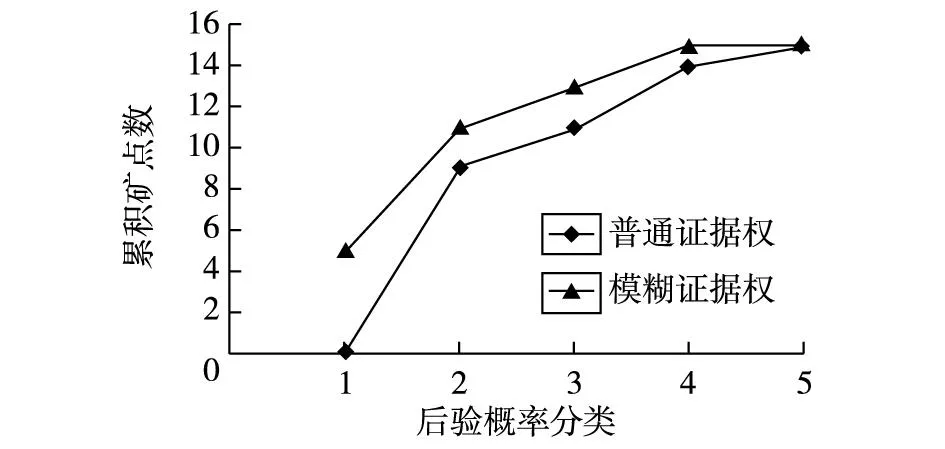
图8　 普通证据权法和模糊证据权法后验概率　　结果分类与累积矿点对比曲线Fig.8　Posterior probability versus cumulative occurrences by the common and fuzzy weights of evidence modeling

3成矿预测应用研究

以大尹格庄金矿床隐伏矿体预测空间为研究对象，采用10 m精度(即体元尺寸为10 m×10 m×10 m)来划分地质空间，利用已知区共96 346个立体单元(其中26 826个含矿单元)作为样本数据，选取断裂面距离场因素(dFV)、断裂面趋势-起伏因素(waF、wbF)、断裂面坡度因素(gF)、断裂面陡缓转换部位综合场因素(fP、fV)和蚀变带场强因素(fA)作为证据图层，对未知区进行成矿预测研究。

3.1　研究区地质概况

大尹格庄金矿是胶东地区蚀变岩型金矿床的典型代表之一，位于招平断裂带的中段，区内地层以太古宇胶东岩群变质岩为主，其次为广泛分布的第四系。矿区西部大面积出露玲珑花岗岩，其中分布有大量不同类型的脉岩。以韧性变形及脆性断裂等为主的多期构造发育，规模大、强度高，变形变质作用复杂。大尹格庄金矿床包含①、②号2个矿体群，以大尹格庄断裂为界，北部为②号矿体群，南部为①号矿体群，它们呈隐伏状态分布于招平断裂带的下盘，矿体的形态、产状及分布严格受招平断裂带的控制。

①号矿体群的主要矿体均赋存在招平断裂带下盘的黄铁绢英岩化花岗质碎裂岩或黄铁绢英岩化碎裂岩蚀变带中，并与主裂面的距离较近，部分紧靠主裂面形成。在蚀变带之外，偶见有零星小矿化体出现。矿体群平面上总体呈较规则的脉状或似层状，沿走向呈舒缓波状起伏变化，在-140 m和-175 m中段以及-380 m中段矿体形态完整、简单，较为稳定，数量少，规模大，反映矿化相对集中。而在-200～-300 m之间，矿体数量增多，规模变小，分布较为分散，单个矿体的形态也变得不规则，以透镜状或不规则状为主。部分地段形成较厚大的矿柱。

②号矿体群位于大尹格庄断裂的北侧，其矿体的变化性比①号矿体大。同时其规模也远比①号矿体群大得多。单个矿体以不规则脉状为主，少数呈透镜体状，沿走向和倾向均呈波状延伸，局部膨缩和分支复合现象明显，在矿体中部形成多个矿体密集区，构成厚大矿体。与①号矿体不同的是，在Ⅱ号矿体分解的高度(-200～-320 m之间)范围内，矿体呈合并趋势，矿化范围变小(走向延伸变短)，但整体厚度却有增大趋势。

3.2　证据图层的选择

大尹格庄金矿床赋存于招平断裂带下盘的绢英岩化花岗岩、绢英岩化花岗质碎裂岩中，区内以大尹格庄断裂为界共控制2个矿体群。两矿体均严格受控于招平断裂带，其产状与招平断裂带一致。招平断裂带是在早期断裂带的基础上，由右行压扭性断裂转化为左行张扭性断裂，使早期的紧闭断裂发展成为张启性断裂，从而为矿液的上移提供了通道，并为金矿的富集、沉淀提供了最佳场所(李子英等，2010)。金矿床分布于招平断裂带内及其下盘的次级断裂构造或裂隙带内，说明招平断裂带既是金矿的导矿构造，也是容矿构造。

根据招平断裂带矿床矿体的空间分布特征和成矿地质条件的分析与归纳，得出下列矿体定位规律：(1) 矿化蚀变带均受韧性剪切带或断裂构造的严格控制。早期的韧性剪切有晚期脆性叠加的构造有利于金矿化。(2) 断裂带蚀变较强且分带明显，一般由内向外依次为黄铁绢英岩-黄铁绢英岩化碎裂岩-绢英岩化花岗质碎裂岩-花岗质碎裂岩-碎裂状花岗岩，其蚀变越强、厚度越大、分带越明显，矿化越好；(3) 断裂面产状及形态起伏变化对矿体的控制。主断裂面由缓变陡处矿体变厚、变富，而断裂面起伏不明显时矿化变弱，矿体厚度变薄；(4) 断层泥对矿液起明显的屏障作用。断层泥沿主断裂面发育且稳定，一般呈灰黑色，断层泥的难渗透性和可塑性，成为含矿热液很难渗透的屏障，使含矿热液在断层泥下盘沉淀聚集成矿；(5) 矿体侧伏规律。矿体侧伏现象是指矿体沿倾向延伸很大，延深远远大于延长。矿体的侧伏主要受断裂构造两盘相对运动过程中产生的启张空间的侧伏制约，而启张空间的侧伏与断裂的性质及运动方式有关，矿体的侧伏反映了成矿流体运移的方向。因此，在矿体的侧伏方向具有良好成矿空间的潜力。

根据上述矿体定位规律，选择如下成矿信息作为证据图层。

(1) 断裂面距离场因素(dFV)。大尹格庄金矿床在成矿过程严格受招平主断裂控制，这种控制直接体现在矿床与主裂面之间的距离上。通过计算垂直方向上矿化单元与主裂面的距离，得到距离场因素，该因素能模拟反映矿化分带的结果，即距离主裂面的矿化强度分布。

(2) 断裂面趋势-起伏因素(waFV、wbFV)。断裂面一般呈舒缓波状，其形态变化地段有利于矿液的富集、矿化的叠加。断裂面的形态尤其是隆起和凹陷形态往往控制着矿体的产出及分布。断裂面趋势-起伏因素主要是揭示断裂面起伏对断裂面周围地质空间的控矿作用影响。经过反复试验，并结合矿化空间分析的结果，选择180 m和360 m作为一级滤波和二级滤波的插值搜索范围半径，对断裂面原始TIN模型进行一级形态滤波和二级形态滤波，对应得到断裂面的一级起伏程度(waFV)、二级起伏程度(wbFV)。

(3) 断裂面坡度因素(gF)。控矿断层的三维形态影响着矿体的空间定位。断裂面的坡度属于断裂面的产状，能够更局部地体现断裂面的产状变化，以及产状变化给成矿提供的微观物理化学环境。通过计算单元到主裂面上最近距离的三角网面片的坡度，得到坡度因素，该因素能模拟反映矿体侧伏的规律。

(4) 断裂面陡缓转换部位综合场因素(fP、fV)。断裂面在倾向方向上的陡缓转换对成矿具有显著作用。陡缓转换的部位也是成矿热液运移异常的地段。矿化富集部位多位于主断裂面由缓变陡的部位，这些部位实际就是破裂加宽地段，矿液汇集于此时流速降低，从而使矿质易于沉淀。

(5) 蚀变带场强因素(fA)。蚀变岩型金矿体一般产出于蚀变带内部，因此矿化场实际是蚀变场的一个子集。对于任意一个矿化单元，其受周围所有蚀变单元的影响，这种影响的强弱受二者距离的约束，因此在一定的球形范围内，采用按距离加权的场来描述矿化单元的蚀变场指标。

3.3　基于普通证据权法的应用

对于证据图层的二值化，采用统计直方图可以比较直观地分析有利于成矿的证据因子。从图9中可以看出：(1) 断裂面距离场因子(dFV)。含矿体元基本处于断裂的下盘，且主要分布于-150～0 m距离范围内，故选择该距离范围作为有利证据因子；(2) 断裂面趋势一级起伏因子(waFV)。含矿体元附近断裂面的局部起伏程度(即一级起伏程度)较小，大部分处于-10～10 m范围内，故选择该起伏范围作为有利证据因子；(3) 断裂面趋势二级起伏因子(wbFV)。含矿体元附近断裂面的整体起伏程度(即二级起伏程度)较小，大部分处于-10～10 m范围内，故选择该起伏范围作为有利证据因子；(4) 断裂面坡度因子(gFV)。含矿体元附近断裂面的坡度较缓，主要分布于24°～48°范围内，故选择该坡度范围为有利证据因子；(5) 断裂面由缓变陡转换场因子(fP)。主要含矿体元分布于断裂面由缓变陡部位场强值为3～7的空间范围内，故选择该场强范围作为有利证据因子；(6) 断裂面由陡变缓转换场因子(fV)。主要含矿体元分布于断裂面由陡变缓部位场强值为-7～-3的空间范围内，故选择该场强范围作为有利证据因子；(7) 蚀变带蚀变场因子(fA)。主要含矿体元分布于蚀变带蚀变场强值为40～100和160～200的空间范围内，故选择该场强范围作为有利证据因子。建立证据因子数据库，将各证据图层二值化，属于有利因子范围的体元赋值为1，不属于该范围的赋值为0。

图9　成矿信息统计直方图Fig.9　Statistical histograms of ore-forming information

利用以上数据库，通过WofE3DSys计算(图3)，将后验概率计算结果导入Voxler中。由图10可见，体元中后验概率最高的为0.544，即该体元含矿的概率为54.4%。经统计，研究区成矿后验概率范围为0.005～0.544，平均值为0.112 1，标准差为0.111 8。26 826个已知含矿体元中的56.7%落在高概率区(P>0.35)。

图10　普通证据权后验概率可视化图Fig.10　Visualization map of posterior probability by the common weights of evidence modeling

3.4　基于模糊证据权法的应用

经WofE3DSys计算(图4)，将后验概率计算结果导入Voxler中，结果如图11。由图11可见，单元格中后验概率最高为0.996，即该单元含矿的概率为99.6%。经统计，研究区成矿后验概率范围为0～0.996，平均值为0.315 3，标准差为0.382 6。26 826个已知含矿体元中的92.9%落在高概率区(P>0.8)。据此，模糊证据权的后验概率比普通证据权高，且准确性也较高。

图11　模糊证据权后验概率可视化图Fig.11　Visualization map of posterior probability by the fuzzy weights of evidence modeling

3.5　成矿远景区圈定

根据上述应用结果，采用模糊证据权方法计算所得到的后验概率图作为成矿远景区圈定的依据。

由大尹格庄矿区已知含矿体元的分布情况(图12)和后验概率图综合分析，共圈定了4个成矿远景区Ⅰ—Ⅳ(图13)：(1) 该远景区位于②号矿体群深部矿体的深部，②号矿体群受招平断裂带控制，该断裂总体走向东北，倾向南东，可能为②号矿体群深部矿体沿招平断裂带倾向方向的深部延伸，含矿概率较大；(2) 该远景区位于②号矿体群深部矿体附近，含矿概率较大；(3) 该远景区位于②号矿体群的东北部，可能为②号矿体群向东北部的延伸；(4) 该远景区位于②号矿体群的北部，可能为②号矿体群向北部的延伸。

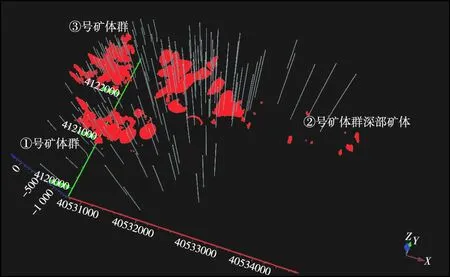
图12　大尹格庄矿区已知含矿体元Fig.12　Elements of the known ore-bearing bodies in the Dayin’gezhuang ore district

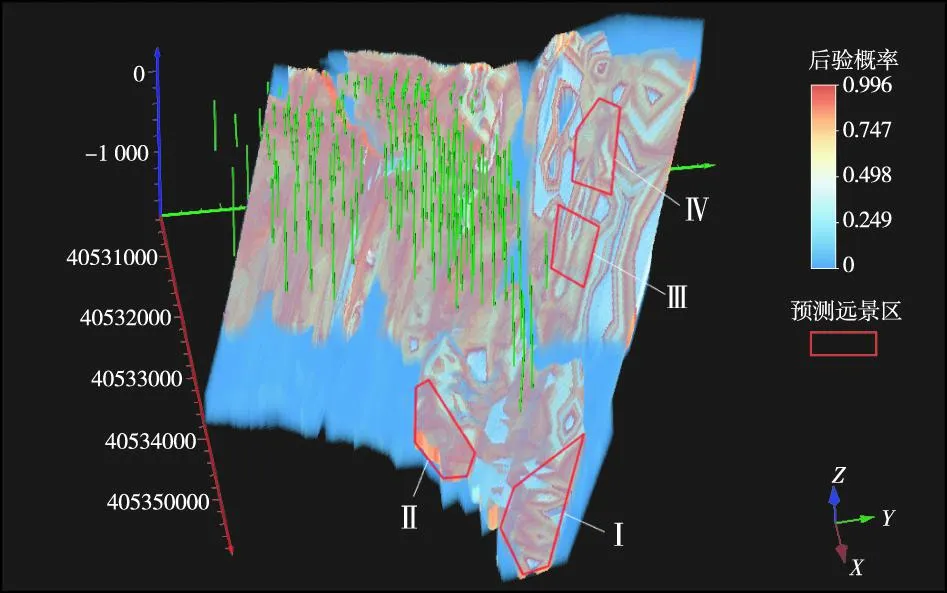
图13　基于模糊证据权圈定的成矿远景区Fig.13　Metallogenic prospects delineated by the fuzzy weights of evidence modeling

4结论

(1) 将传统二维证据权的建模方法改进为适用于三维空间下隐伏矿体立体预测的建模方法，并分别探讨了普通证据权和模糊证据权法建模的思路和方法。以Visual Studio 2010为开发平台，在Access 2003中建立多元地学空间数据库，设计并开发可进行证据因子选择、因子权重计算及后验概率计算的证据权软件WofE3DSys。其输出结果可在Voxler中进行三维可视化展现。

(2) 为验证WofE3DSys的准确性，通过利用ArcGIS软件中的Arc-WofE模块进行成矿预测，以招平断裂带中段及其周围区域为研究对象，将该预测结果与本次研究中WofE3DSys软件计算所得到的普通证据权法结果进行比较，2种结果相一致，说明WofE3DSys准确性较高。

(3) 以招平断裂带大尹格庄金矿为实例，选取对成矿有利的成矿信息为证据图层，计算后验概率，最终得到成矿预测结果，共圈定4个成矿远景区。实现了对三维空间下证据权法的一次探索，为将来该证据权法在其他矿区的成矿预测提供了现实依据。

虽然得出了上述结论，但还存在下列局限性：(1) 证据因子的选择。三维空间下的成矿预测在证据因子的选择方面与二维空间相比较局限。证据因子数量的多少与质量的好坏，在一定程度上会影响最终后验概率的可靠性与准确性，还需加强对矿区成矿信息提取的研究；(2) 成矿预测结果。所得到的预测结果只是以概率的形式呈现，可以考虑改进方法，进而可以定量地预测出未知区体元的品位和金属量。

参考文献：

陈建平,吕鹏,吴文,等.2007.基于三维可视化技术的隐伏矿体预测[J].地学前缘,14(5):54-61.

丁清峰,孙丰月.2006.基于专家证据权重法的成矿远景区划与评价：以东昆仑地区金矿为例[J].地质科技情报,25(1):41-46.

胡光道,陈建国.1998.金属矿产资源评价分析系统设计[J].地质科技情报,17(1):45-49.

胡官兵,刘祥旭,韩天成.2010.证据权法在个旧锡多金属矿床综合信息成矿预测中的应用[J].矿业工程,8(3):9-11.

刘世翔,薛林福,郄瑞卿,等.2007.基于GIS的证据权重法在黑龙江省西北部金矿成矿预测中的应用[J].吉林大学学报:地球科学版,37(5):889-894.

李卫东,余志伟,单新建,等.2009.基于GIS和证据权模型的矿产勘探信息系统[J].辽宁工程技术大学学报:自然科学版,28(3):382-385.

李子英,张瑞忠,周春生,等.2010.胶东大尹格庄金矿床控矿构造系统[J].金属矿山,62(3):86-90.

刘岳,陈翠华,何彬彬.2011.基于证据权模型的东昆仑五龙沟金矿潜力预测[J].中国矿业大学学报,40(2):298-304.

毛先成.2006.三维数字矿床与隐伏矿体立体定量预测研究[D].湖南长沙:中南大学.

肖克炎,葛艳.1999.成矿预测中证据权重法与信息量法及其比较[J].物探化探计算技术,21(3):223-226.

肖克炎,李楠,孙莉,等.2012.基于三维信息技术大比例尺三维立体矿产预测方法及途径[J].地质学刊,36(3):229-236.

赵鹏大,李紫金,胡光道.1992.重点成矿区三维立体矿床统计预测：以安徽月山地区为例[M].湖北武汉:中国地质大学出版社.

张生元,成秋明,张素萍,等.2009.加权证据权模型和逐步证据权模型及其在个旧锡铜矿产资源预测中的应用[J].地球科学:中国地质大学学报,34(2):281-286.

赵增玉,潘懋,梁河.2010.二值证据权(WofE)模型岩溶塌陷区划研究[J].北京大学学报:自然科学版,46(4):594-600.

张宝一,毛先成,周尚国,等.2012.基于GIS的证据权重法在桂西南地区优质锰矿成矿预测中的应用[J].地质找矿论丛,26(4):359-366.

ASADI H H,HALE M. 2001. A predictive GIS model for mapping potential gold and base metal mineralization in Takab area,Iran[J]. Computers & Geosciences,27(8):901-902.

AGTERBERG F P,CHENG QIUMING.2002.Conditional independence test for weights-of-evidence modeling[J].Natural Resources Research,11(4):249-255.

BONHAM-CARTER G F,AGTERBERG F P,WRIGHT D F.1990.Weight of evidence modelling: a new approach to mapping mineral potential[C]//Statistical Applications in the Earth Science.Vancouver, CAN: Geological Survey of Canada,171-183.

CHENG QIUMING,AGTERBERG F P.1999.Fuzzy weights of evidence method and its application in mineral potential mapping [J].Natural Resources Research,8(1):27-35.

CHEN YONGLIANG.2004.MRPM: three visual basic programs for mineral resource potential mapping [J].Computers & Geosciences,30(9):969-983.

CHENG QIUMING.2008.Non-linear theory and power-law models for information integration and mineral resources quantitative assessments [J].Mathematical Geosciences,40(5):503-532.

FALLARA F,LEGAULT M,RABEAU O.2006.3-D integrated geological modeling in the Abitibi Subprovince (Quebec, Canada): techniques and applications[J].Exploration and Mining Geology,15(1/2):27-43.

FELTRIN L.2008.Predictive modelling of prospectivity for Pb-Zn deposits in the Lawn Hill Region,Queensland, Australia[J].Ore Geology Reviews,34(3):399-427.

HARRIS J R,WILKINSON L,GRUNSKY E C.2000.Effective use and interpretation of lithogeochemical data in regional mineral exploration programs: application of Geographic Information Systems (GIS) technology[J]. Ore Geology Reviews,16(3/4):107-143.

JOUNEL A G.2002.Combining knowledge from diverse sources: An alternative to traditional data independence hypotheses [J].Mathematical Geology,34(5):573-596.

PORWAL A,GONZALEZ-ALVAREZ I,MARKWITZ V,et al.2010.Weights-of-evidence and logistic regression modeling of magmatic nickel sulfide prospectivity in the Yilgarn Craton, Western Australia[J].Ore Geology Reviews,38(3):184-196.

WANG GONGWEN,ZHANG SHOUTING,YAN CHANGHAI,et al.2011.Mineral potential targeting and resource assessment based on 3D geological modeling in Luanchuan region, China [J].Computers & Geosciences,37(12):1976-1988.

Modeling method of weights of evidence in three-dimensional space and its application to resource prediction

PAN Shi-chen1,2, MAO Xian-cheng1,2

(1.Key Laboratory of Metallogenic Prediction of Nonferrous Metals, Ministry of Education, Central South University, Changsha 410083, Hunan, China; 2.School of Geosciences and Info-Physics, Central South University, Changsha 410083, Hunan, China)

Abstract：This study discussed the modeling idea and methods suitable for mineral potential prediction in 3D space based on the common weights of evidence modeling, in order to study the practical metallogenic prognosis application of weights of evidence in 3D space. In addition, this study established a multi-geological spatial database in Access 2003 with the Visual Studio 2010 as the develop platform, and then used the software WofE3DSys, which can select the factors and calculate the weights and posterior probability. The output of this software can realize 3D visualization visible in Voxler. The result calculated by WofE3DSys reconciled with the output of Arc-WofE in the context of anomaly delineation, which proves the accuracy of WofE3DSys. Finally, taken the Dayin’gezhuang gold deposit as example, this study selected ore-controlling factors as evidence layers to do metallogenic prognosis. This research can be regarded as an exploration of weight of evidence modeling in 3-dimensional space, which has provided practical evidence for metallogenic prediction in other mining areas.

Keywords：3D modeling; weights-of-evidence; posterior probability; metallogenic prognosis; Shandong