常利率下的双险种的再保险风险模型*



常利率下的双险种的再保险风险模型*

沈焰焰

(福建船政交通职业学院，福建 福州 350007)

摘要:〗文章引入一类常利率因素下的双险种的再保险风险模型，讨论了初始准备金为μ、利率为δ、双险种的再保险的破产概率，并给出破产概率的表达式和Lundberg上界．

关键词:利率；双险种；再保险；破产概率

本文在文献[1-3]的基础上建立了常利率因素下双险种的再保险风险模型，并得到初始准备金为u时破产概率ψ(u)的明确表达式和Lundberg上界．这不仅加强了模型的现实描述能力，而且对保险公司的安全经营及其监督也具有非常重要的意义．

1模型的建立

设保险公司的盈余过程为

U(t)=

u(1+δ)+(c1t-c1R1t+c2t-c2R2t)(1+δ)-

其中，U(t)为保险公司在时刻t的盈余；u=U(0)>0为保险公司在经营初期的准备金；ci>0(i=1,2)为保险公司第i种险种单位时间内收取的保费，即保费率；ciRi(i=1,2)为原保险人单位时间支付第i种险种给再保险人保费；Xki(i=1,2)表示保险公司第i种险种第k次的索赔额；Rki(i=1,2)表示再保险公司第i种险种第k次的补偿给原保险人的赔偿额；Ni(t)(i=1,2)则表示时刻t为止保险公司第i险种所发生的理赔总次数.

我们作如下的假设：

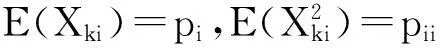
假设2{N1(t):t≥0}是以λ1为参数的possion过程．{N2(t):t≥0}是以λ2为参数的possion过程．{N1(t):t≥0}与{N2(t):t≥0}相互独立．

假设3为保证保险公司稳定经营要求：令

H(t)=(c1+c2-c1R1-c2R2)·(1+δ)t-

称{H(t),t≥0}为盈利过程．通常要求E(H(t))>0由独立性可知

由于

本研究拟采用LC-MS/MS法对原发性高脂血症人群的血浆中9种胆汁酸的分布情况进行分析，并通过与健康人群相关胆汁酸进行比较，了解人体的血脂水平与其血浆胆汁酸分布情况的相关性，对比分析原发性高脂血症人群与健康人群血浆中胆汁酸的组成与含量差异，以期为原发性高脂血症人群的治疗和饮食结构调整提供有力的客观性依据。

E(H(t))=E{(c1+c2-c1R1-c2R2)·(1+δ)t-

(c1+c2-c1R1-c2R2)·(1+δ)t-

E(Xk1-Rk1)E(N1(t))-E(Xk2-Rk2)E(N2(t))=

(c1+c2-c1R1-c2R2)·(1+δ)t-

(λ1(p1-q1)+λ2(p2-q2))t>0

从而

(c1+c2-c1R1-c2R2)·(1+δ)>

λ1(p1-q1)+λ2(p2-q2)

定义1T=inf{t|t≥0,Uδ(t)<0}称T为破产发生时刻．

定义2ψ(u)=P{Tδ<∞|Uδ(0)=u}称ψ(u)为初始准备金为u时的破产概率．

2主要结果

{H(t),t≥0}盈利过程的性质

性质1{H(t),t≥0}具有平稳的独立增量

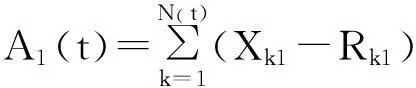
H(ti)-H(ti-1)=

(c1+c2-c1R1-c2R2)·(1+δ)(ti-ti-1)-

[A1(ti)-A1(ti-1)]-[A2(ti)-A2(ti-1)]

由于(ti-ti-1),A1(ti)-A1(ti-1),A2(ti)-A2(ti-1)是相互独立的，所以{H(t),t≥0}具有独立的增量．又因为

H(t+j)-H(t)=(c1+c2-c1R1-c2R2)·(1+δ)(t+j-t)-[A1(t+j)-A1(t)]-[A2(t+j)-A2(t)]对于一切的t≥0，(t+j-t)=j,且A1(t+j)-A1(t),A2(t+j)-A2(t)分别具有相同的分布，所以对于一切的t≥0，H(t+j)-H(t)也具有相同的分布．{H(t),t≥0}具有平稳的增量．因此{H(t),t≥0}具有平稳的独立增量．

性质2E(H(t))=(c1+c2-c1R1-c2R2)·(1+δ)t-(λ1(p1-p11)+λ2(p2-p21))

Var(H(t))=λ1t(p11+q11)+λ2t(p22+q22)

Var(H(t))=

Var((c1+c2-c1R1-c2R2)·(1+δ)t)+

性质3存在正数r，使得E(e-rH(t))<∞

定理1存在函数g(r)使得E(e-rH(t))=etg(r)证明

e-r(c1+c2-c1R1-c2R2)·(1+δ)t·eλ1t(MXk1-Rk1(r)-1)·eλ2t(MXk2-R2(r)-1)=

e-r(c1+c2-c1R1-c2R2)·(1+δ)t+λ1t(MXk1-Rk1(r)-1)+λ2t(MXk2-R2(r)-1)

令

g(r)=-r(c1+c2-c1R1-c2R2)·(1+δ)+

λ1(MXk1-Rk1(r)-1)+λ2(MXk2-Rk2(r)-1)

则E(e-rH(t))=etg(x)，其中MXk1-Rk1(r)，MXk2-Rk2(r)分别是Xk1-Rk1，Xk2-Rk2的矩母函数．

定理2方程g(r)=0存在唯一的正解R，称R为调节系数．

证明

g(r)=-r(c1+c2-c1R1-c2R2)·(1+δ)+

λ1(MXk1-Rk1(r)-1)+λ2(MXk2-Rk2(r)-1)

g′(r)=-r(c1+c2-c1R1-c2R2)·(1+δ)+

g″(r)=λ1M″Xk1-Rk1(r)+λ2M″Xk2-Rk2(r)

MXk1-Rk1(0)=MXk2-Rk2(0)=1,

g(0)=0,

g′(0)=-(c1+c2-c1R1-c2R2)·(1+δ)+

λ1(p1-q1)+λ2(p2-q2)<0,

由Cauchy-Schwarz不等式知g″(0)>0，故g(r)为凸函数，g(r)=0有两个解，除去r=0，另外存在唯一的正解R.

定理3设X(t)=e-RU(t),则{X(t),t≥0}是秧，其中R为定理2中的调节系数．

证明

X(t)=e-RU(t)=

e-R((1+δ)u+H(t))=e-R(1+δ)u·e-RH(t)

X(0)=e-R(1+δ)u·e-RH(0)=e-R(1+δ)u是一个常数，即X(t)=X(0) ·e-RH(t)

令Y(t)=-RH(t)，由性质1可知{Y(t),t≥0}是一初值为零的，且具有齐次独立增量的随机过程．所以MH(t)(r)=E(erH(t))=(MH(1)(r))t,t≥0而

MH(1)(r)=

er(c1+c2-c1R1-c2R2)·(1+δ)+λ1(MXk1-Rk1(r)-1)+λ2(MXk2-R2(r)-1)

由定理2可知，MH(1)(-R)=e0=1，即E[e(-RH(1))]=e0=1，

E[|X(t)|]=|X(0)|E[e-RH(t)]=

|X(0)|E[e-RH(1)]t=|X(0)|<∞

E[X(t)|X(r):r≤s]=

E[X(s)e-RH(t)+RH(s)|X(r):r≤s]=

X(s)E[e-RH(t)+RH(s)|X(r):r≤s]=

X(s)E[e-RH(t-s)|X(r):r≤s]=X(s)

所以{X(t),t≥0}是秧．

其中MH(t)(r)是H(t)的矩母函数．

上述不等式称为Lundberg不等式，e-R(1+δ)u称为ψ(u)的Lundberg上界．

E[X(t∧T)]=E[X(0)]=e-R(1+δ)u

根据全期望公式

e-R(1+δ)u=E[X(t∧T)]=

E[X(t∧T)|T≤t]P(T≤t)+

E[X(t∧T)|T>t]P(T>t)=

E[X(t)|T≤t]P(T≤t)+

E[X(T)|T>t]P(T>t)

e-R(1+δ)u=E[X(t∧T)]=

E[X(t∧T)|T≤t]P(T≤t)+

E[X(t∧T)|T>t]P(T>t)=

E[X(t)|T<∞]P(T<∞)+

E[X(∞)|T=∞]P(T=∞)=

E[X(T)|T<∞]P(T<∞)

即上式可变为ψ(u)

参考文献：

[1]刘丹,王志福.常利率下带干扰的双险种风险模型的破产概率[J].商丘师范学院学报,2013(6):22-24.

[2]李静霞,王永茂.常利率因素下的双险种风险模型[J].数学理论与应用,2008(3):101-106.

[3]陈丽.常利率下的再保险风险模型的破产概率[J].重庆理工大学学报,2012(3):114-119.

[4]蔡秋娥,廖基定.复合Poisson-Geometric过程的性质及简单应用[J].湖南工业大学学报,2010(1):40-42.

[5]熊双平.带干扰的索赔次数为复合Poisson-Geometric过程的负风险和模型[J].经济数学,2007(3):37-41.

(责任编辑:陈衍峰)

A Risk Model of Double-type-reinsurance with Costant Interest

SHEN Yan-yan

(FujianchuanzhengcommunicationCollege,Fuzhou,Fujian350007,China)

Abstract:A double-type of the reinsurance of the insurance risk model with constant interest is introduced . Initial reserve u, interest rate δ and ruin probability are discussed. Meanwhile, the explicit expression for the ruin probability and its Lundberg upper bound are proposed.

keywords:interest; double line; reinsurance; ruin probability

中图分类号：O212

文献标志码：A

文章编号：1008-7974(2015)06-0024-03

作者简介：沈焰焰,福建莆田人,讲师．

基金项目：2010年福建省交通科技发展项目“基于物联网的物流系统中关键问题的GRASP算法研究”(201011)；2014年省教育厅社科类项目“海西经济区贸易结构对经济增长的影响路径的研究”(JAS14585)；2015年省教育厅社科类项目“风险理论在保险公司经营中的应用”(JAS150868)

收稿日期：*2015-06-12

DOI:10.13877/j.cnki.cn22-1284.2015.12.008