LTE系统咬尾卷积码的概率-代数联合译码算法

李婉，李建平

(中国传媒大学信息工程学院，北京 100024)



LTE系统咬尾卷积码的概率-代数联合译码算法

李婉，李建平

(中国传媒大学信息工程学院，北京 100024)

摘要：充分利用咬尾卷积码编码器的线性信息，将WAVA这种概率译码同代数译码算法进行级联，得出一种新的复杂度较低的概率-代数联合译码算法，经仿真得出，该算法使得咬尾卷积码的纠错性能较单一概率译码获得进一步提升。

关键词：咬尾卷积码；环绕维特比算法；概率代数联合译码

1引言

随着移动通信技术的不断发展及其用户需求的逐年增加，移动通信系统必须满足更大的系统容量，更低的成本以及更广泛的覆盖，支持多天线的系统要求。为此，3GPP提出了3GPP空中技术的长期演进(LTE)。在信道编码技术上，LTE系统采用了咬尾卷积码和Turbo码[1]。

咬尾卷积码是一种特殊的卷积码。咬尾编码就是用信息序列的最后几个比特来初始化编码器的寄存器。这样在编码结束的时候，编码器的寄存器状态和初始编码时的状态一样，这就是所谓的咬尾[2]。咬尾编码所能提供的优势主要是能够消除用已知比特来初始编码器所导致的码率损失。由于其编码器和译码器结构相对简单，处理延时小，主要应用于小码块控制信息和对时延敏感的数据传输，如LTE系统中的广播信道和控制信道等低数据率信道[3]。

卷积码的译码技术可以大致分为两类：代数译码和概率译码。代数译码是利用编码本身的代数结构进行译码，不考虑信道的特性。概率译码主要是基于信道统计特性进行译码，没有充分考虑到卷积码作为线性码的代数结构关系。从信息论的角度分析，条件信息的不充分利用必然导致结论出现偏差。上述两类译码算法对于卷积码线性性质和信道特性信息的不充分利用也必然导致译码算法性能的降低[4]。

由于咬尾卷积码的最优译码——最大似然(ML)译码的复杂度较高，实际应用中，通常采用一些次优译码算法。本文基于一种次优译码环绕维特比算法(WAVA)和代数译码中的反馈译码，参考文献[4]中的概率-代数联合译码方案，得出一种针对LTE系统的咬尾卷积码的优化译码算法。该算法将传统的分组码的代数译码算法同WAVA这种概率译码算法结合起来，充分利用咬尾卷积码的线性性质和信道统计信息，使其纠错能力得到进一步提升，并通过仿真验证了这一点。

2咬尾卷积码的译码算法

2.1　环绕维特比算法

咬尾卷积码的译码算法有很多，比如较早的Bar-David算法和最大似然算法，以及后续的循环维特比算法(CVA)。本文采用的是基于CVA算法的低复杂度改进算法环绕维特比算法[5](WAVA)。其译码流程图如图1所示：

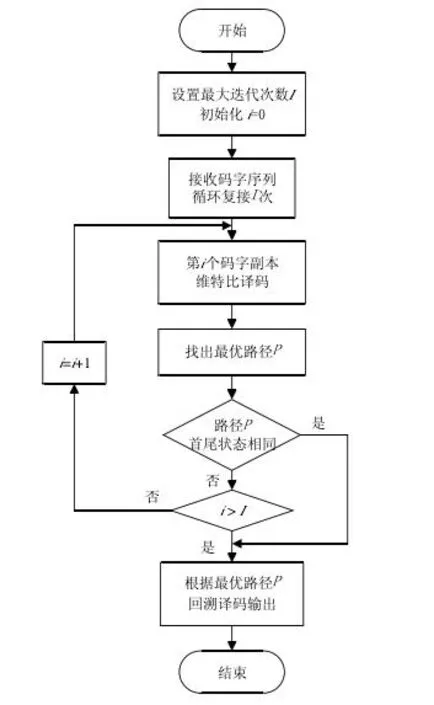
图1　WAVA算法流程图　

循环维特比算法(CVA)输出的总是具有最大度量路径的码字，但是当码字的首尾比特受到噪声的破坏比较严重时，具有最大度量的路径首尾状态将不再相等[6]-[8]。WAVA 方法有效地克服了这一情况。WAVA的译码过程如下：

1.设所有初始状态SI的分支度量si=0(si∈SI)；

2.对码块进行Viterbi译码，找出具有最大度量的路径并检测它的首尾状态是否相等，即SI=SF是否成立；

4.在第i(i>1)次迭代开始时，用上次迭代结束时的状态度量信息初始化第i-1次迭代的初始状态度量，并对码块Viterbi译码，如果具有最大度量路径的首尾状态相同，则停止译码，否则，继续步骤 5；

5.重复步骤4 直到找到具有相同首尾状态的最优路径，或是达到了最大迭代次数I；

6.如果最优路径的首尾状态不相等，则判断其他路径是否首尾状态相等，如果找到这一路径，则输出对应的码字，否则输出具有最大度量的路径。

2.2　代数译码算法

代数译码是一类利用编码本身的代数结构进行译码的算法。它利用卷积码的线性特征，通过伴随式指明接收码组中的错码位置，从而纠正错码。这里首先介绍伴随式的概念。(n0，k0，m)卷积码的伴随式S定义为

S=R*HT=(C+E)*HT=E*HT

(1)

其中C为发送的码序列，E为信道的错误图样，R为接收到的码序列，HT为卷积码的校验矩阵H的转置。

当S全为0，说明此时间单位收到的子组(第0子组)前的第m子组内无错，但不能说明第m-1子组至第0子组内无错误，因为第m-1至第0子组还与以后各子组间存在约束关系。因此，在to时刻求得的S，只能用于纠正其前m个时间单位的第m子组个错误。因而，卷积码的伴随式计算和译码是以子组为单位进行的，每一个时间单位，仅完成一个子组的译码。

卷积码的代数译码就是从收到的序列R=C+E中，确定发送的序列C或是相应的信息序列M。这就要求译码器首先计算出伴随式S，并由S计算出错误图样E。最后有C=R-E，对于二进制码而言，即相当于C=R+E。

图2中显示了代数译码的一般工作原理[9]。

图2　代数译码的一般工作原理　

其工作过程大致如下：

1.由收到的序列R中分成两个序列，信息序列M与校验序列P。M序列送入信息缓存器中寄存，并送入伴随式计算电路，通过一个与发端相同的编码器，重新生成校验元。将新的校验元与收到的校验序列进行比较，得到的结果送入伴随式寄存器中。

2.当接收完第m+1段子组后，伴随式寄存器中的伴随式送入错误图样检测器中，以确定此时刻前第m个时间单位内收到的子组(第0子组)的信息位内错误图样E。将错误图样E与之前寄存的信息序列M相减，即得到译码后的信息序列M’=M-E。

3.由于卷积码的编码过程中，第0子组的信息元会对其后m段子组的校验元产生影响。为了消除错误码元对其后译码产生的影响，需要将错误信息反馈给伴随式进行修正。这种反馈修正的译码方式称为反馈译码。若译码后不对伴随式进行修正，则称为定译码。

4.第0子组的信息元译出后，其后的信息元也以同样的方法依次译码。每接收n0个码元，译出k0个信息元。

5.若为非系统码，则得到已纠过错的码段C后，再将其与生成矩阵的逆G-1相乘，得到信息组M。

2.3　概率代数联合译码

咬尾卷积码的概率代数联合译码基本思路即是将概率译码——环绕维特比算法(WAVA)同代数译码结合起来形成新的级联译码的形式。联合译码算法的编码器如图3所示。其中m为输入的信息序列，经过编码器E1编码得到d1，d2，d3三个校验序列。同时另d3进入编码器E2继续编码，输出的码字序列经过选择器MUX，输出新的校验序列d4，此处，选择器MUX起到了增信删余的作用。由图可以看出，经编码后的码字其码率R=1/4。

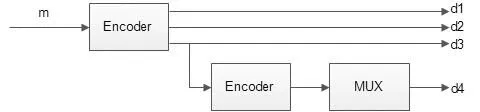
图3　联合译码算法的编码器结构　

联合译码算法的译码流程如图4所示。收到的序列R首先经过环绕维特比译码，得到纠错序列C’和信息序列M’，在经由代数译码得到最终的信息序列M。

图4　联合译码算法的译码器结构　

这之中，WAVA算法主要利用信道统计信息，通过网格图进行译码。这种译码方式比较充分地利用了信道统计信息，即概率信息，却没有对咬尾卷积码编码结构中的线性结构进行充分利用。为了弥补这一部分信息的不完全利用，进一步增大译码增益，需要在WAVA译码器后级联一个代数译码器。代数译码器的译码原理即是通过码字间的线性约束结构进行译码。由于卷积码本身的编码特性，当前译码的信息不仅对当前，还会对其后的m(m为卷积码的约束长度)段码字产生影响。故而在当前码段译出的同时，要添加一条反馈路径，纠正后续码组的伴随式，来消除当前错误对后续译码的影响。

这种译码方式对于系统和非系统咬尾卷积码同样适用，且不会因为非系统码没有独立信息位，而在代数译码的过程中增加对生成矩阵求逆的步骤。从而使代数译码部分较之经典的代数译码过程减少了时延。

值得一提的是，由于代数译码模块的输入是经环绕维特比译码后的纠错序列，因而具有相对较低的误码率，即纠错序列C’和信息序列M’中的错误比特可以认定为呈现零散分布状态，在代数译码的纠错能力之内。所以本联合算法中采用反馈译码的形式，比之没有反馈的定译码方式，进一步提升了纠错性能。

3仿真实验与结果分析

仿真在MATLAB平台下进行，仿真所采用的咬尾卷积码为LTE系统中所采用的咬尾卷积码，码率R为1/3，生成多项式g=(133，171，165)[10]其编码器结构图5所示。

图5　咬尾卷积码编码器结构图　

仿真信道采用加性高斯白噪声(AWGN)信道，调制方式为LTE系统中广播信道(BCH)规定的QPSK调制。LTE系统中咬尾卷积码作为低数据率编码方案，其数据块长度在20~60bit之间，仿真选取20和60bit的两种数据块，在信噪比为0~9db范围内进行仿真。将接收端译码后的信息序列同发送的信息序列相比较，得到误比特率。以传统的环绕维特比译码结果为参照，将联合译码结果同其对比，可得到仿真结果如图6，7.由图可以看出，随着信噪比逐渐升高，联合译码所带来的增益也随之变大，但在低信噪比条件下，联合译码的纠错性能低于传统的WAVA译码。这是由于卷积码本身的纠错性能是有限的，它只能纠正有限个独立随机错误，当信噪比过低时，差错可能会成串出现[9]，卷积码就无法保持其编码增益，甚至出现“越纠越错”的情况。但当信噪比大于3dB，即WAVA译码的输出序列具有足够低的误码率时，联合译码的增益则呈现出逐渐增大的趋势。同时，对比图6和图7可以看出，当数据块增大时，联合译码算法会获得更大的增益。

图6　WAVA和联合译码的BER性能比较，N=20　

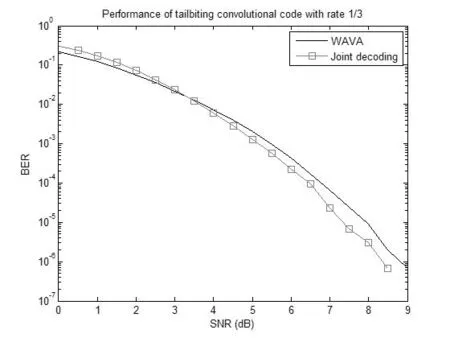
图7　WAVA和联合译码的BER性能比较，N=60　

4结论

本文的LTE系统咬尾卷积码概率-代数联合译码在咬尾卷积码的环绕维特比算法基础上，利用了卷积码编码器的线性结构，级联了反馈译码的代数译码模式，提升了译码性能。从仿真结果图6，7中可以看出，在信道中信噪比增加时(误比特率降低)或数据块N变大时，联合译码算法带来的增益更大。本联合译码算法相比于传统的概率译码算法带来了较为明显的译码增益，可以适用于LTE系统的各类低数据率信道，同时本算法以卷积码的译码算法为基础，可以扩展到以卷积码为基础的Turbo码等各类级联码译码算法中，实现更加广泛的应用。

参考文献

[1]3GPP TS 36.212 v8.8.0，multiplexing and channel coding [S]. Geneva：3GPP，2009.

[2] Shao R Y. Decoding of linear block codes based on their tailbiting trellises and efficient stopping criteria for turbo decoding[D].Univ of Hawaii at Manoa，Honolulu，HI，1999.

[3]陈发堂.LTE系统中咬尾卷积码的编译码算法仿真及性能分析[J].计算机应用研究，2010，27(09)：3338-3340.

[4]李建平.Turbo码概率-代数联合译码算法[J].电子学报，2003，31(12)：1847-1850.

[5]Shao R Y，Shu Lin，Marc P C.Two decoding algorithms for tailbiting codes[J].IEEE Trans on Communications，2003，51(10)：1658-1665.

[6]Wang Q，Bhargava V K. An efficient maximum likelihood decoding algorithm for generalized tail biting convolutional codes including quasi-cyclic [J]. IEEE Trans on Communications，1989，37(8)：875-879.

[7]Ma H H，Wolf J K.On tailbiting convolutional codes[J]. IEEE Trans Commun，1986，34：104-111.

[8]Cox R V，Sundberg C E. An efficient adaptive circular Viterbi algorithm for decoding generalized tailbiting convolutional codes[J].IEEE Trans Veh Technol，1994，(43)：57-68.

[9]王新梅.纠错码——原理和方法[M].西安：电子科技大学出版社，2001：394-398.

[10]3GPP TS 36.212-3rd-2009，Generation Partnership Project；Technical Specification Group Radio Access(E-UTRA)；Multiplexing and Channel Coding(Release 8)[S]. Sophia Antipolis Valbonne：3GPP，2013：11-13.

(责任编辑：王谦)

Joint Probability-algebraic Decoding for Tail-biting Codes Uused in LTE System

LI Wan，LI Jian-ping

(Information Engineering School，Communication University of China，Beijing 100024，China)

Abstract：To fully make use of the information on the algebra structure of the tail-biting codes，we combined the WAVA algorithm with the algebraic decoding，and propose a new joint probability-algebraic decoding algorithm. Simulation results show that，compared with the single probability decoding，the new algorithm has better performance on the error correction.

Keywords：tail-biting codes；WAVA；joint probability-algebraic decoding

作者简介：李婉(1990-)，女(汉族)，辽宁省葫芦岛人，中国传媒大学硕士研究生.E-mail：liwancuc@163.com

收稿日期：2015-09-09

中图分类号：TN911.22

文献标识码：A

文章编号：1673-4793(2015)05-0035-05