自适应差分进化算法优化BP神经网络的时间序列预测*
2016-01-26王林,彭璐,夏德等
自适应差分进化算法优化BP神经网络的时间序列预测*
通信地址:430074 湖北省武汉市华中科技大学管理学院Address:School of Management,Huazhong University of Science and Technology,Wuhan 430074,Hubei,P.R.China
王林1,彭璐1,夏德2,曾奕1
(1.华中科技大学管理学院,湖北 武汉 430074; 2.武汉理工大学管理学院,湖北 武汉 430070)
摘要:针对BP神经网络学习算法随机初始化连接权值和阈值易使模型陷入局部极小点的缺点,设计了一种自适应差分进化算法优化BP神经网络的混合算法。该混合算法中,差分进化算法采用自适应变异和交叉因子优化BP神经网络的初始权值和阈值,再用预寻优得到的初始权值和阈值训练BP神经网络得到最优的权值和阈值。首先对改进的自适应差分进化算法运用测试函数进行性能测试,然后用一个经典时间序列问题对提出的混合算法进行了检验,并与一般的神经网络、ARIMA预测模型及其它混合预测模型进行了对比,实验结果表明,本文提出的混合算法有效并且明显提高了预测精度。
关键词:时间序列预测;BP神经网络;差分进化算法
1引言
时间序列预测是预测系统中很重要的一个领域,应用最广泛的一种时间序列模型是ARIMA(AutoregressiveIntegratedMovingAverage),此模型预先假设待研究的时间序列是线性的,但是现实世界中的系统通常是非线性的,很难假设模型的形式。近年来,神经网络模型因其灵活的非线性建模能力、较强的自适应性、学习能力和大规模并行计算能力,被广泛地应用于时间序列预测研究中,其中,前向型神经网络是应用最多的时间序列预测模型,BP神经网络BPNN(BackPropagationNeuralNetwork)又是前向型神经网络中应用最多的一种[1]。BP神经网络又名误差反向传播网络,它是一种通过信息前向进行传递而误差反向进行传播来修正误差的多层映射网络。通常,单隐含层的BP神经网络能够以任意精度逼近任何非线性函数[2],这一优势使其在复杂的非线性系统预测中备受青睐。
传统BP神经网络学习算法是一个梯度下降或其变形的有导师学习算法[1],先随机初始化网络的权值和阈值,利用训练样本,通过网络输出值与实际值的均方误差反向传播来调节网络的权值和阈值,使得均方误差梯度下降,当误差达到设定的目标时,BP神经网络的权值和阈值得到确定,即网络的训练过程结束。这种学习算法的缺点是初始的权值和阈值对最终的训练结果影响很大,导致训练结果极易陷入局部极小点而不是全局最优,进而使得网络的预测精度不能达到很高的程度。为了克服传统BP神经网络易陷入局部极小点的缺点,众多学者提出了不同的改进方法来优化传统BP神经网络的初始权值和阈值。YamJYF等[3]在线性代数的基础上设计了一种优化前向神经网络初始权值的算法,采用优化后的初始权值可使初始的培训误差极大程度地减小,从而使达到设定误差所需的培训次数也得到减少。IraniR等[4]用遗传算法对BP神经网络初始权值和阈值进行了优化。李松等[5]用改进粒子群算法优化BP神经网络进行短时交通流预测。
差分进化DE(DifferentialEvolution)算法是一种随机启发式搜索算法,其基于差分的简单变异和交叉操作产生新的个体,然后将新产生个体与原来个体的适应值进行比较,适应值较优的个体将保存下来,且能利用个体局部信息和群体全局信息协同搜索,以其实用性、鲁棒性和强大的全局寻优能力在许多领域都有很好的应用[6,7]。邓华等[8]用DE结合BPNN对多因素影响的产品成本进行了预测。本文设计了嵌入自适应SDE(Self-adaptiveDE)算法的BP神经网络预测模型(SDE-BPNN),为了克服基本DE算法早熟和后期搜索迟钝等缺点,采用了自适应DE变异和交叉因子。本文用被广为采用的检验非线性预测模型效果的时间序列问题[9]对SDE-BPNN进行了检验,与ZhangGP[10]、KhasheiM[11]和WangL[12]提出的预测模型相比,SDE-BPNN的预测结果比这三个模型都要优。
2BP神经网络预测基本原理
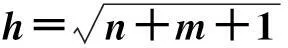
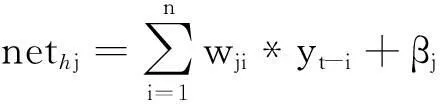
(1)
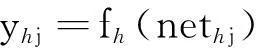
(2)
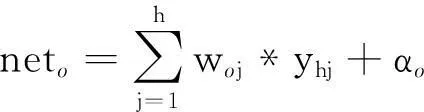
(3)
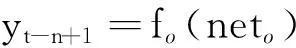
(4)
其中,n为输入层神经元数,h为隐含层神经元数,wji和woj分别为输入层与隐含层神经元之间、隐含层与输出层之间的连接权值,βj和αo分别为隐含层与输出层神经元的阈值,fh和fo分别为隐含层与输出层的转移函数。本文隐含层转移函数选取tansig函数:f(x)=2/(1+e-2x)-1;输出层转移函数选取purelin函数:f(x)=x。
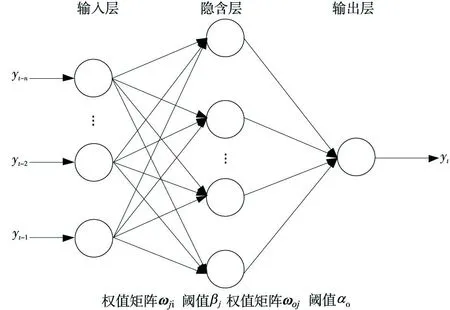
Figure 1 BPNN structure with single hidden layer图1 单隐含层BPNN结构图
3差分进化算法流程分析
3.1 标准DE算法
标准DE算法包括初始化、变异、交叉和选择操作。
(1)初始化:DE算法采用实数编码方法,先设定种群规模Np和基因维数D,以及每个基因的变化范围[Umin,Umax],然后用式(5)随机初始化种群,产生种群个体xij:
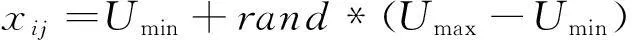
(5)

(6)
其中,G为进化代数,个体序号r1、r2和r3随机选择产生且互不相同,且r1、r2和r3与目标向量序号i也不一样。因此,一般种群规模NP≥4。F为变异因子,众多文献中建议的取值范围为[0,2],用以控制差分矢量的缩放。
(3) 交叉操作:交叉操作按照式(7)产生:

(7)
其中,rand(j)∈[0,1]为均匀分布的随机产生的数;j表示第j个基因,CR为交叉因子;randn(i)∈[1,2,…,D],为随机选择生成的参数,以保证实验矢量至少能够从变异矢量中获得一维变量。
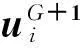
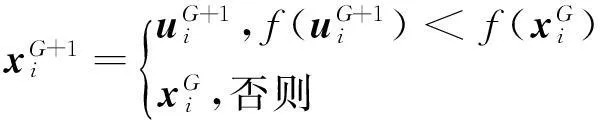
(8)
3.2 两种自适应DE算法及其性能测试
3.2.1 两种自适应DE算法
(1)ADE(AdaptiveDE):仅采用自适应变异因子。
变异因子决定了偏差向量的放大比例,变异因子太大,算法搜索效率会很低,求解全局最优解的精度低;如果变异因子过小,又不能保证种群的多样性,很容易出现早熟的现象[12]。因此,将引入自适应的变异因子,变异因子随着迭代次数的增加,变异率将逐渐减小,初期较大的变异因子能够保证种群多样性,后期较小的变异因子则能保留优良个体,自适应变异因子按照式(9)产生:
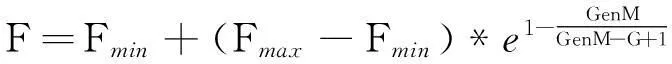
(9)
其中,Fmin表示变异因子的最小值,Fmax表示变异因子的最大值,GenM表示最大的迭代代数,G则为当前进化的代数。
(2)SDE(Self-adaptiveDE):采用自适应交叉和变异因子。
在ADE基础上,引入自适应交叉因子。交叉因子随着迭代次数的增加,交叉率也动态变化,初期较大的交叉因子保证全局范围的变异情况,后期较小的交叉率更关注局部的收敛情况。自适应交叉因子的设计如式(10)所示:
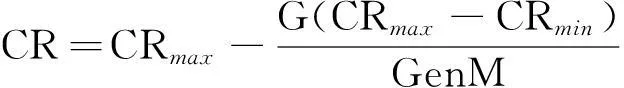
(10)
其中,CRmin表示交叉参数的最小值,CRmax表示交叉参数的最大值。
3.2.2 性能测试
(1) 函数介绍。
为了比较SDE、ADE和DE的性能,选择四个常用的多峰函数进行测试,函数细节如下:
F1∶Rastrigin函数:

F2∶Griewangk 函数:

其中,xi∈[-600,600],n=30。该函数为多峰函数,在xi=0处取得全局最小值0。
F3∶Ackley’s Path 函数:


其中,xi∈[-1,1],n=30。该函数为多峰函数,在xi=0处取得全局最小值0。
F4∶Weierstrass 函数:

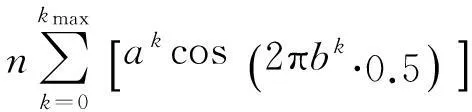
其中,a=0.5,b=0.3,kmax=30,xi∈[-0.5,0.5],n=10。该函数为多峰函数,在xi=0处取得全局最小值0。
(2) 测试结果。
用SDE、ADE和DE三种算法对以上四个函数进行优化计算。具体参数设置为:Np=100,DE中F=0.6,CR=0.6;ADE中Fmin=0.2,Fmax=0.9,CR=0.6;SDE中Fmin=0.2,Fmax=0.9,CRmin=0.1,CRmax=0.6;最大迭代次数均设为1 000,每次运行20次。由表1知,SDE算法的平均值和方差均比DE和ADE算法的值好,这显示了SDE算法具有较好的性能。

Table 1 Result comparison of the three algorithms
4SDE优化BP神经网络的预测模型(SDE-BPNN)


(11)
其中,yt是BPNN的目标输出。
SDE-BPNN混合算法的流程为:
Step 1初始化。对种群规模、最大迭代次数、变异因子和交叉因子进行初始化,另根据式(5)初始化种群。
Step 2判断是否达到迭代结束条件(全局极小值达到设定的精度要求或者达到设定的最大迭代次数),如果是则停止迭代并且输出最优个体;否则,转到下一步。
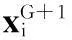
Step 4重复Step 3,直到得到下一代种群。
Step 5评价下一代种群的适应度值,最小适应度值即为全局极小值,对应的个体即为全局最优个体。
Step 6G=G+1,返回Step 2。
Step 7将自适应DE优化输出的最优个体作为BPNN的初始权值和阈值,用训练集训练网络。
Step 8输入测试集,用训练后的网络进行预测。
5对比算例与分析
5.1 实验条件
(1)实验数据:选取文献[9]中自1821~1934年在加拿大马更些河被捕获的猞猁时间序列数据。最先是Elton 和 Nicholson详细描述了200多年前在加拿大各地区捕获的猞猁数量的波动情况,表明猞猁数量变化的平均周期为9.6年[13]。如图2所示,这组数据多次被用于检验非线性预测模型的有效性,这里同样对数据进行预处理,方法是对原数据取以10为底的对数,取预处理后的前100个数据为训练集,用于SDE预寻优和BPNN训练,后14个数据为测试集验证混合预测模型的有效性。预测结果与Zhang G P[10]、Khashei M[11]和Wang L[12]提出的预测模型的预测结果进行比较。
Figure 2 Canadian lynx series (1821~1934)图2 加拿大猞猁数据时间序列(1821~1934)
参照文献[12],预测性能指标选取平均误差平方和MSE和平均绝对值误差MAE,如式(12)所示:
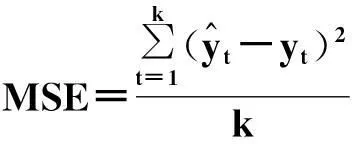
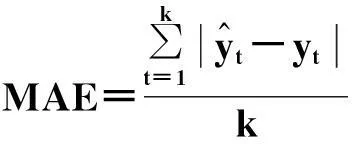
(12)

(2)实验参数设置。

5.2 实验结果分析
SDE-BPNN预测结果如图3所示,图中数据是预处理后的实际测试数据与预测结果的比较。其与ARIMA模型、ANNs及其他混合模型的预测效果比较如表2、表3所示。

Figure 3 Comparison between pratical test data and the SDE-BPNN predict results(logarithmic test sample data set)图3 SDE-BPNN预测猞猁数据结果(测试集)

模型MSEMAEARIMA0.0204860.112255ANNs0.0204660.112109ARIMA-ANNs[10]0.0172330.103972ARIMA-ANNs[11]0.0136090.089625ADE-BPNN[12]0.0103920.070623SDE-BPNN0.0068330.066110
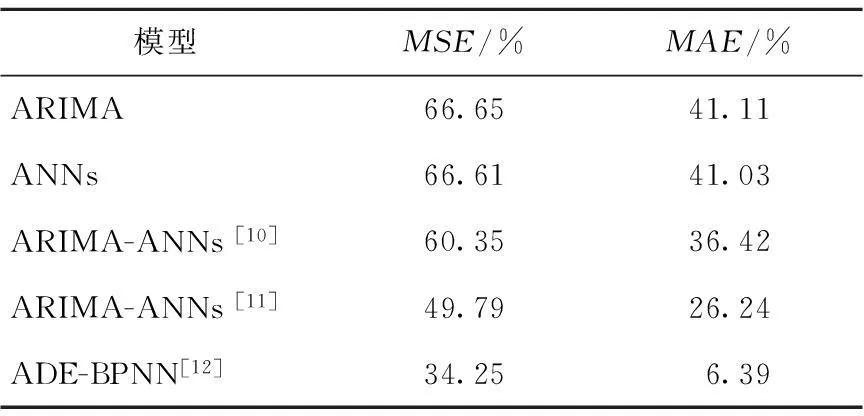
Table 3 Improvement comparison of
从表3可以看出,对于MSE指标,SDE-BPNN算法的预测效果比ARIMA、ANNs模型提高了将近67%,比文献[10]提出的模型要高出60.35%,比文献[11]提出的模型要高出49.79%,比文献[12]提出的模型要高出34.25%;对于MAE指标,SDE-BPNN混合算法比其他五种模型分别提高了41.11%、41.03%、36.42%、26.24%和6.39%。
6结束语
本文将DE算法与BP神经网络结合,用于时间序列预测,主要工作和贡献如下:为了克服传统BP学习算法易使训练过程陷入局部极值点的缺点,改善其预测精度。本文先用具有强大全局寻优能力的自适应DE算法进行全局预寻优,然后用传统学习算法进行深度寻优,训练BP神经网络。测试函数表明了自适应DE算法的有效性,并通过一个具有明显非线性特点的时间序列样本验证了SDE-BPNN混合算法的有效性,预测精度得到了明显提高。
本研究将两种新颖的智能算法相结合应用于时间序列预测,理论上拓展了非线性时间序列预测理论,扩大了DE算法的应用范围。本文提出的混合预测方法可用于帮助企业进行销售预测等,具有广泛的适用性和较强的应用价值。以后将把本文提出的预测方法和ARIMA模型结合,用来满足其他方面的预测需求,如旅游需求和零售业销售预测等。
参考文献:附中文
[1]Zhang G,Patuwo B E,Hu M Y. Forecasting with artificial neural networks:The state of the art [J]. International Journal of Forecasting,1998,14(1):35-62.
[2]Aslanargun A,Mammadov M,Yazici B,et al. Comparison of ARIMA,neural networks and hybrid models in time series:Tourist arrival forecasting [J]. Journal of Statistical Computation and Simulation,2007,77(1):29-53.
[3]Yam J Y F,Chow T W S. A weight initialization method for improving training speed in feedforward neural network [J]. Neurocomputing,2000,30(1):219-232.
[4]Irani R,Nasimi R. Evolving neural network using real coded genetic algorithm for permeability estimation of the reservoir [J].Expert Systems with Applications,2011,38(8):9862-9866.
[5]Li Song,Liu Li-jun,Zhai Man. Prediction for short-term traffic flow based on modified PSO optimized BP neural network[J].Systems Engineering-Theory & Practice,2012,32(9):2045-2049. (in Chinese)
[6]Onwubolu G,Davendra D. Scheduling flow shops using differential evolution algorithm [J]. European Journal of Operational Research,2006,171(2):674-692.
[7]Qu H,Wang L,Zeng Y R. Modeling and optimization for the joint replenishment and delivery problem with heterogeneous items[J]. Knowledge-Based Systems,2013,54:207-215.
[8]Deng Hua, Zhao Hui. Prediction of product cost based on DE-BP algorithm[J]. Computer Engineering and Applications,2009,45(3):233-234. (in Chinese)
[9]Campbell M J,Walker A M. A survey of statistical work on the Mackenzie River series of annual Canadian lynx trappings for the years 1821-1934 and a new analysis [J].Journal of the Royal Statistical Society (Series A),1977,140:411-431.
[10]Zhang G P. Time series forecasting using a hybrid ARIMA and neural network model[J]. Neurocomputing,2003,50:159-175.
[11]Khashei M,Bijari M. An artificial neural network (p,d,q) model for timeseries forecasting [J]. Expert Systems with Applications,2010,37(1):479-489.
[12]Wang L,Zeng Y,Chen T. Back propagation neural network with adaptive differential evolution algorithm for time series forecasting [J]. Expert Systems with Applications,2015,42(2):855-863.
[13]Elton C,Nicholson M. The ten-year cycle in numbers of the lynx in Canada [J]. The Journal of Animal Ecology,1942,11:215-244.
[5]李松,刘力军,翟曼. 改进粒子群算法优化BP 神经网络的短
时交通流预测[J]. 系统工程理论与实践,2012,32(9):2045-2049.
[8]邓华,赵辉. DE-BP 神经网络对产品成本预测的研究[J].计算机工程与应用,2009,45(3):233-234.

王林(1974-),男,湖北枣阳人,博士,教授,研究方向为智能优化算法。E-mail:wanglin982@163.com
WANG Lin,born in 1974,PhD,professor,his research interest includes intelligent optimization algorithms.

彭璐(1991-),女,湖北荆州人,硕士生,研究方向为物流工程。E-mail:pengluhust@163.com
PENG Lu,born in 1991,MS candidate,her research interest includes logistics engineering.

夏德(1974-),男,湖北红安人,博士,教授,研究方向为管理科学与工程。E-mail:xiadetiger@126.com
XIA De,born in 1974,PhD,professor,his research interest includes management science and engineering.

曾奕(1990-),女,湖南益阳人,硕士生,研究方向为供应链管理。E-mail:zengy200810@126.com
ZENG Yi,born in 1990,MS candidate,her research interest includes supply chain management.
BPneuralnetworkincorporatingself-adaptivedifferentialevolutionalgorithmfortimeseriesforecasting
WANGLin1,PENG Lu1,XIA De2,ZENG Yi1
(1.SchoolofManagement,HuazhongUniversityofScienceandTechnology,Wuhan430074;
2.SchoolofManagement,WuhanUniversityofTechnology,Wuhan430070,China)
Abstract:It is easy for a BP neural network (BP-NN) to be trapped into a local minimum point for the time series forecasting problem. To improve the forecasting accuracy, we design a hybrid algorithm which combines the self-adaptive differential evolution algorithm (SDE) with the BP-NN. We adopt the SDE algorithm to search for global initial weights and thresholds of the BP-NN. These values are then employed to further search for the optimal weights and thresholds. The performance of the proposed SDE algorithm is verified through benchmark functions and a well-known real data set is used to verify the effectiveness of the hybrid algorithm. Compared with general neural network, ARIMA and other hybrid models,experimental results indicate that the proposed algorithm can be an effective way to improve forecasting accuracy.
Key words:time series forecasting;BP neural network;differential evolution algorithm
作者简介:
doi:10.3969/j.issn.1007-130X.2015.12.012
中图分类号:TP301
文献标志码:A
基金项目:中央高校基本科研业务费资助项目(HUST:2014QN201)
收稿日期:修回日期:2015-03-10
文章编号:1007-130X(2015)12-2270-06
