无源侦察中高速目标轨迹跟踪研究
2016-01-23项利萍中国电子科技集团公司第三十八研究所合肥230088
徐 伟,谢 梦,项利萍(中国电子科技集团公司第三十八研究所,合肥230088)
无源侦察中高速目标轨迹跟踪研究
徐伟,谢梦,项利萍
(中国电子科技集团公司第三十八研究所,合肥230088)
摘要:导弹和卫星等高速目标的跟踪是反导雷达系统中的核心问题。传统的轨迹跟踪方法不能很好适应无源侦察设备对于高速目标的跟踪。本文提出了一种高速目标纯角度轨迹跟踪方法。该方法在初始跟踪段使用平均加权方式,并在一定迭代次数后采用Singer滤波,有效地降低了整个跟踪阶段的均方根误差,取得较好效果。
关键词:高速目标的跟踪;角度跟踪;平均加权; Singer滤波
0 引言
导弹和卫星轨迹的跟踪包括导弹和卫星飞行状态的估计、导弹和卫星飞行速度和高度的测量、导弹的落点的判断等。导弹和卫星的轨迹跟踪程序算法复杂,是整个反导雷达系统的关键所在[1]。
目标跟踪时滤波模型的选择对跟踪的效果起着十分重要的作用。运动模型的不匹配,如使用匀速模型跟踪机动目标,往往会导致滤波收敛速度较慢、滤波发散等后果[2]。Singer模型将目标加速度视为时间相关的随机过程,并通过设置机动时间常数和目标加速度方差等先验参数,可以适用于各种机动类型的目标跟踪问题[3-4]。文献[5]提出一种纯方位观测的航迹不变量目标跟踪算法。但是,该方法需要预知目标的运动方式,对于导弹跟踪并不适合。文献[6]提出了一种基于无源定位系统的航迹处理方法,利用了Singer滤波进行航迹跟踪,但在航迹起始区域并不能保证均方根误差较低。
导弹进行试验发射时通常会在弹体上安装通讯传输天线,在导弹运行过程中实时将各种信息发送到地面站进行分析。通过对导弹上的传输天线发射的无线电信号进行稳定跟踪,可将无线电信号进行完整地截获,得出该导弹的运动参数等信息,达到无线电侦察的作战任务。无线电侦察设备着重于对目标发射的无线电信号进行接收,所以对无线电信号的轨迹跟踪主要涉及到方位角和俯仰角的跟踪。无源侦察设备在发现目标后转入窄带数字波束形成,进行无线电信号的测向任务。窄带波束通常覆盖的空域有限,常常仅有1°~2°的方位角和俯仰角范围,而导弹等目标飞行速度很快,飞出窄带波束覆盖的空域范围的时间仅有0.5 ~1.5 s。若没有进行稳定的轨迹跟踪,及时调整窄带波束指向,将导致跟踪的无线电信号丢失,进而可能导致整个侦察任务的失败。特别是在刚刚发现目标时,常常在Kalman滤波器还没完成收敛观测目标就飞出了窄带波束的覆盖空域。为了完成对高速目标的跟踪,要求无源侦察设备的轨迹跟踪具有目标轨迹起始迅速、跟踪稳定、全过程跟踪误差小的特点。
综合上述因素,本文提出了一种无源设备高速目标轨迹跟踪方法。该方法可以有效解决高速目标跟踪的要求。与传统的轨迹跟踪算法相比,本文的方法可以较好地解决轨迹跟踪的目标起始不稳定问题,具有一定的鲁棒性,便于工程实现。
1 Kalman Singer模型滤波
线性离散系统的状态空间方程:
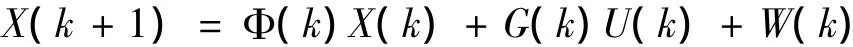
其中目标状态方程为
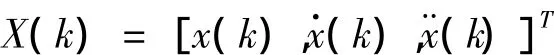
其中,x(k)为当前滤波位置,x·(k)为当前滤波速度,x¨(k)为当前的滤波加速度。
状态转移矩阵
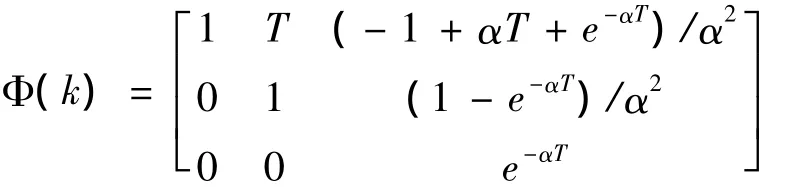
其中,T为两次观测之间间隔时间,参数α=1/τm是机动时间常数τm的倒数,参数σ2= E[a(t)2]是目标加速度的方差。按照Singer的建议,对飞机慢速转弯,τm=60 s;对于逃避机动,τm=20 s;对大气扰动,τm=1 s。Singer还对机动加速度a(t)的分布作以下假定: a(t)为0的概率为P0,a(t)为最大加速度±amax的概率为Pmax,且服从均匀分布,按此假设,可以得到
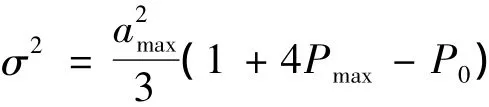
输入控制加权矩阵G(k)和过程噪声分布矩阵W(k)在实际运算中常均取为0矩阵。观测噪声矩阵和过程噪声的协方差阵需要根据实际情况进行调整。本方法中选取观测噪声矩阵R = rms2,其中rms表示均方根(Root Mean Square)。连续时间离散化的过程噪声w(k)的协方差阵(过程噪声的协方差阵):
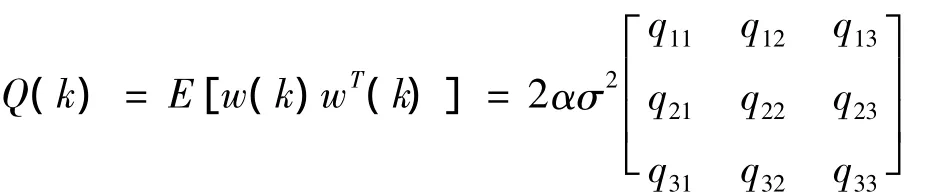
其中

2 平均加权的误差估计
若输入的测向信号的测向噪声服从均值为0、方差为σ2I的正态分布,即Noise~N(0,σ2I)。
采用滑窗方式,每次滑窗向后滑动一个测向信号,再进行加权平均。滑窗的大小为M时,将M个原始测向信号取平均后形成凝聚测向信号,则凝聚测向信号噪声应服从均值为0、方差为σ2I/M的正态分布,即Noise~N(0,σ2I/M)。
当给出平均加权的误差范围W时,若要求99.73%的凝聚点迹噪声误差在W之内(即3σI范围内),即3σI/槡M<W,可推出M>9σ2I/W2。
在理想情况下,可将输入的均方根误差近似当作标准差,即当输入的rms = 0.6≈σI,若需要达到的精度为W =0.3,则凝聚点个数M =36。即当参与凝聚的点个数大于36个时,可将输出的均方根误差降低为rms =0.1,并达到预期误差范围。
3 高速目标轨迹跟踪算法与实验
本文提出的高速目标轨迹跟踪算法如下:
(1)在发现目标初跟阶段,分别对方位角和俯仰角的测向信息利用平均加权方式进行轨迹跟踪。
(2)对方位向和俯仰向分别利用Singer滤波,再根据设置,在一定迭代步骤K之后使用Singer进行轨迹跟踪。
当平均加权时,由于对最初的M个测向点未完成加权过程,此时轨迹处理不输出轨迹滤波结果,不向波束调度软件发送波束调度信息。
本文的仿真实验环境如下:设置试验导弹速度约为4 km/s,距离无源侦察设备大约为300 km,方向为近似切向飞行,无源设备的测向数据率为每秒1000次,方位向的测向误差均方根(RMS)为0.1°,俯仰向的测向误差均方根(RMS)为0.5°。无源侦察设备要求跟踪的方位向的误差范围控制在0.05,俯仰向的误差范围控制在0.25,则选定平均加权的滑窗大小M = 36。将Singer滤波中参数α取为0.05,σ2取为0.6125。
基于经验值,本文算法在2000步前采用平均加权方法,在2000步后直接采用Singer滤波方法。
图1为方位向残差比较,其中图1(a)为平均加权的残差,通过计算可以得到方位向的平均加权误差的均方根(RMS)为0.0168,比0.1°降低了约5.95倍,与公式理论值相符合,同时可以发现平均加权的误差较为稳定。图1(b)为Singer滤波的残差,可以发现在刚开始运行时,残差误差较大,大约在1300步以后,算法才能收敛结束,Singer滤波残差均方根(RMS)为0.0179,收敛后为0.0093。图1(c)为本文方法的残差,在初始运行时,采用平均加权方法作为轨迹滤波结果,并以此进行波束调度。本文方法整个阶段的残差均方根(RMS)为0.0099,降低了整个阶段的RMS值。
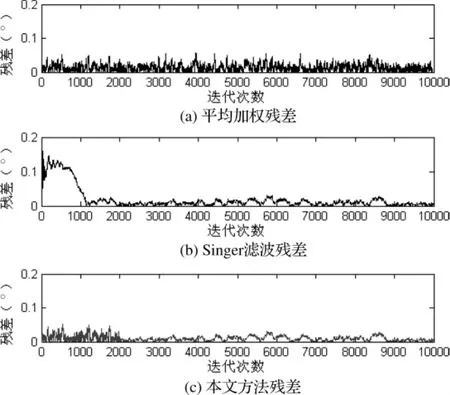
图1 方位向残差比较
图2为俯仰向残差比较,其中图2(a)为平均加权的残差,通过计算可以得到方位向的平均加权误差的均方根(RMS)为0.084,比0.5°降低了约5.95倍,与公式理论值相符合。图2(b)为Singer滤波的残差,可以发现在刚开始运行时残差误差较大,大约在2000步以后算法才能收敛结束,Singer滤波残差均方根(RMS)为0.0478,收敛后为0.0347。图2(c)为本文方法的残差,在初始运行时采用平均加权方法作为轨迹滤波结果,并以此进行波束调度,本文方法整个阶段的残差均方根(RMS)为0.0387,降低了整个阶段的RMS值。
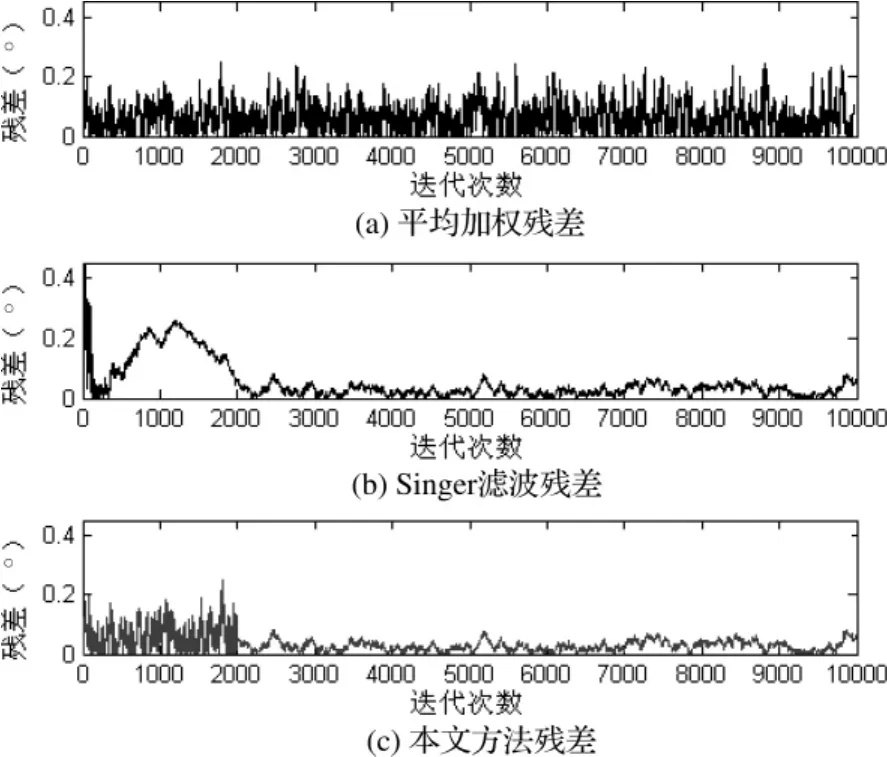
图2 俯仰向残差比较
图3为对仿真弹道的二维跟踪结果,其中图3(a)为输入的原始测向值,图3(b)为平均加权的结果,图3(c)为Singer滤波结果,图3(d)为本文方法结果,从图中可以看出,本文方法有效降低了对于高速运动目标起始段的误差,同时在跟踪段里基于Singer滤波进行了平滑的跟踪。通过实验可以发现,平均加权的rms误差较为恒定,Singer滤波的初始段rms误差较大,收敛后rms误差较低;本文方法在初始段使用平均加权方式,并在一定迭代次数后,采用Singer滤波,有效地降低了整个跟踪阶段的rms误差,取得较好效果。
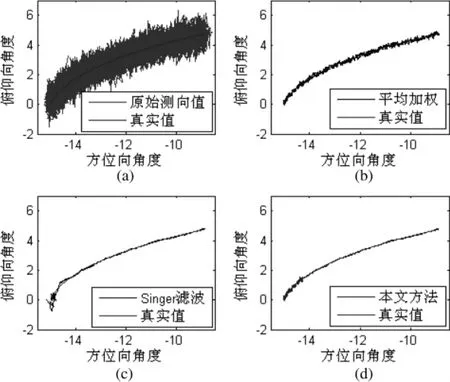
图3 仿真弹道二维滤波结果比较
4 结束语
本文研究了无源侦察中高速目标纯角度轨迹跟踪问题,分析了平均加权方法的误差范围推到;结合Singer滤波方法,提出了一种高速目标轨迹跟踪算法,并进行了算法的实验性能评估。实验结果表明,该方法关于平均加权误差范围的推导有效,并可以稳定跟踪高速目标;与使用单一参数的Singer模型相比,该算法的跟踪精度更高,具有良好的实验性能,适合工程实现。
参考文献:
[1]钮俊清,单奇,任清安,等.跟踪弹道导弹全阶段的可变多模型方法[J].雷达科学与技术,2011,9(3):224-231.
[2]何友,修建娟,张晶炜,等.雷达数据处理[M].2版.北京:电子工业出版社,2009.
[3]Singer R A.Estimating optimal tracking filter performance for manned maneuvering targets[J].IEEE Transactions on Aerospace and Electronic Systems,1970,6(4):473-483.
[4]X Rong Li,Vesselin P.Survey of Maneuvering Target Tracking.Part I: Dynamic Models[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(4):1333-1364.
[5]刘进忙,姬红兵,左涛.纯方位观测的航迹不变量目标跟踪算法[J].西安电子科技大学学报(自然科学版),2008,35(1):49-53.
[6]贾铁燕,杜宇峰,吴素丽.基于无源定位系统的航迹处理[J].舰船电子对抗,2007,30(6): 8-15.
Research on high-speed target tracking in a passive reconnaissance system
XU Wei,XIE Meng,XIANG Li-ping
(No.38 Research Institute of CETC,Hefei 230088)
Abstract:Tracking high-speed targets such as missiles and satellites is the core issue in the antimissile radar system.The conventional methods cannot satisfy the requirements of the passive reconnaissance system for the high-speed target tracking.A high-speed angle-only target tracking method is presented.The average weighting method is adopted in the initial period,and then the Singer filter is used after some iterative steps,which can effectively reduce the RMS error of the whole tracking process and obtain good results.
Keywords:high-speed target tracking; angle tracking; average weighting; Singer filter
作者简介:徐伟(1984-),男,工程师,博士,研究方向:雷达数据处理及雷达软件设计;谢梦(1986-),女,助理工程师,硕士,研究方向:雷达软件设计与软件测试;项利萍(1985-),女,工程师,博士,研究方向:雷达软件设计。
收稿日期:2015-01-03
文章编号:1009-0401(2015)01-0061-04
文献标志码:A
中图分类号:TN958.97
