一种唯相位加权降低天线副瓣技术研究

丛友记，卞美琴，简　玲(中国船舶重工集团公司第七二四研究所，南京211153)



一种唯相位加权降低天线副瓣技术研究

丛友记，卞美琴，简玲
(中国船舶重工集团公司第七二四研究所，南京211153)

摘要:通过分析几种优化阵列副瓣算法的特点，提出将差分进化算法与模拟退火方法相结合的方法，实现了唯相位加权降低阵列天线副瓣。采用快速傅里叶变换法提高计算阵列天线方向图的效率。为了证明该方法的有效性，给出了40×40均匀阵列的唯相位加权低副瓣优化结果，阵列天线副瓣唯相位加权优化后达到了-22.13 dB。

关键词:唯相位加权;低副瓣;阵列天线

0　引言

低副瓣是雷达天线的重要技术指标之一。这种特性不仅可以克服杂波干扰，而且可以降低被敌方发现的概率。如果对阵列天线的激励不作任何加权处理，其第一副瓣电平理论值大约为－13.4 dB，达不到相控阵雷达对副瓣电平的要求。经典降低副瓣的方法有幅度加权法，如切比雪夫综合方法、泰勒综合方法等［1］。这些方法可以较好地降低天线副瓣，但在工程应用中会增加馈电网络的复杂性，降低天线主波束的增益。降低天线副瓣常用的方法还有密度加权法，相比单纯的幅度加权该方法可以减少能量损失，但增加了布阵设计与馈电网络的复杂性。

唯相位加权法是指仅通过控制阵元的激励相位就能得到目标方向图的方法。该方法通过移相就可以实现加权，便于计算机控制且可以减小馈电网络设计难度从而降低成本，工程实现比较简单。然而，由于唯相位加权实现低副瓣问题在数学上属于非线性优化问题，目前还未取得相应的解析解，这给研究工作带来了很大的困难。文献［2］采用相位扰动的方法来降低阵列副瓣，这种方法收敛缓慢且容易收敛停滞。本文比较总结了模拟退火算法与差分进化算法在解决降低阵列天线副瓣问题的特点，综合两种算法提出了一种唯相位加权降低副瓣的优化方法，算例表明了该方法的有效性。

1　算法介绍

1.1问题背景

假定阵列天线辐射单元方向图完全相同时的情况下(当阵列规模较大时，该假定与工程实际类似)，如图1所示的x－y平面上K×L个辐射单元组成的矩形栅格平面阵列，设第(k，l)个辐射单元的激励电流值I(k，l)，天线方向图可以表示为

FF(u，v)= EP(u，v)·AF(u，v)

式中，AF(u，v)为阵列的阵因子，EP(u，v)为天线阵列中的天线单元方向图，且

式中

其中，dx和dy分别表示沿x和y方向上的单元间距，λ为自由空间波长。而I(k，l)= A(k，l)exp(jφ(k，l))，A(k，l)、φ(k，l)分别是阵列单元的幅度、相位。唯相位加权实现低副瓣问题的实质就是寻找一组最优的设计参数φ(k，l)，使式(1)计算出来的方向图副瓣电平最低。

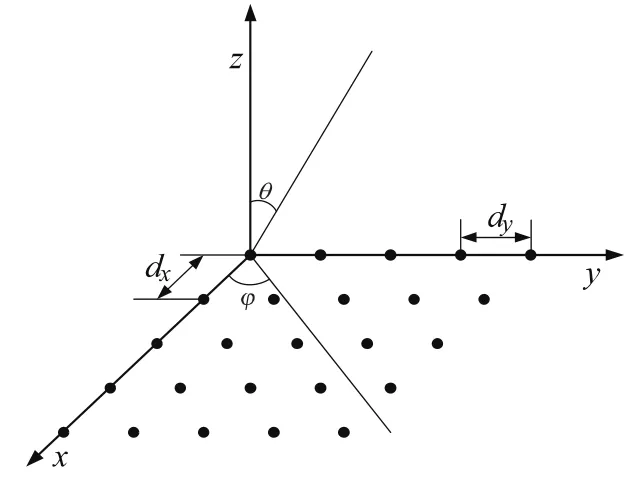
图1　平面阵列天线结构示意图

由于该问题没有解析解，因此本文将重点放在优化算法的研究上。在数学上针对优化问题有多种解决方法，如梯度算法、牛顿迭代法、线性规划法等等。这些算法往往由于实际条件限制或者容易陷入局部最优解的缺陷，不适合多参数非线性问题的优化。为了解决不连续、非线性优化问题，基于模拟自然界现象的人工智能型优化算法——遗传算法、粒子群算法、模拟退火算法等陆续被提出来［3-5］。这些算法在解决非线性优化问题方面具有简单通用、适应性强等特点。

1.2差分进化算法(DE)

差分进化算法起源于Ken Price求解切比雪夫多项式拟合问题时提出的矢量差分思想。经过Storn和Price的修改、完善最终形成差分进化算法。经典的差分进化算法流程如下［6］:

(1)种群初始化，产生N个初始种群V;

(2)使用差分变异算子将初始种群变异操作，对每一个优化向量生成一个新的变异向量。该变异算子具有如下形式:其中V(n)，opt为父代种群中最佳个体，变异因子β是用于控制差分放大率的常数;

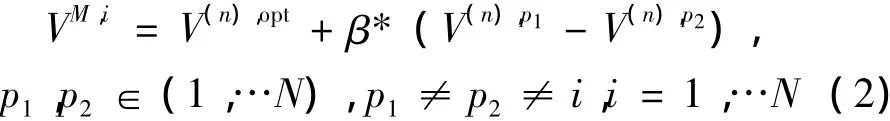
(3)交叉操作，将V(n)，i与其对应的变异个体按一定概率进行交叉操作，生成子代个体VC，i:其中γ为区间［0，1］中的随机数，pcross为确定变异个体取代父代个体的概率;

(4)选择操作。将交叉操作产生的子代个体与父代个体进行比较。如果子代个体适应值小于父代个体，则子代个体取代父代个体，否则父代个体在下一代中保留;

(5)终止操作。如果子代种群中的最佳个体已经达到优化目标，或当前迭代次数达到最大迭代次数，则算法终止，否则返回第(2)步继续迭代优化。

1.3模拟退火算法(SA)

模拟退火算法的核心思想是模拟热力学的原理，在高温下的流体慢慢冷却下来，热能便会逐渐消失形成晶体。对于此系统来说，晶体状态是能量的最低状态。模拟退火算法将最低能量状态类比成问题的最优解，从初始解开始迭代，随着迭代过程解的能量不断减小(降温过程)，最后达到最终的“结晶”状态——问题的解。算法由初始解开始，在当前解的邻域内搜解，并以一定概率接收比当前适应度差的解，其接收概率随着温度的降低而降低，具体的算法流程如图2所示。

图2　模拟退火算法流程图

采用模拟退火算法优化天线副瓣时，首先随机产生一组阵列天线激励相位向量，在此向量基础上扰动得到一组新的激励向量，利用评价函数判定是否接受新解，最终若优化副瓣满足预设指标或者迭代次数达到预设值时迭代停止优化完成。

1.4算法描述

为了比较两种优化算法的特点，本文对30单元规模、间距0.6λ的一维线阵进行唯相位加权副瓣优化仿真试验。这里优化适应度函数设置为

Fitness = W*(SLL－SLL0)

其中，SLL0为副瓣优化目标，SLL为当前优化副瓣，W为放大系数。仿真试验中取W =100，SLL0=－25 dB，差分进化算法种群数设为100，迭代900次，模拟退火算法迭代900次。图3给出了两种算法收敛曲线的对比。

图3　模拟退火与差分进化算法收敛比较

通过两组曲线可以看出，差分进化算法收敛速度快，但很容易收敛停滞，而模拟退火算法搜解能力较强，但收敛缓慢。为了将两种优化方法的优点结合，取长补短，本文提出将差分进化(DE)与模拟退火(SA)算法相结合的混合优化算法，提高了优化算法的优化效率。该混合优化算法步骤如下:

(1)随机产生多组初始的相位激励分布向量(Y0，Y1，…，YN);

(2)将(Y0，Y1，…，YN)采用差分进化算法优化后得到当前的最优相位激励分布Y*best;

(3)将Y*best利用模拟退火算法优化得到此次优化的最优相位激励Zbest。

按照上述步骤针对该实例，其中差分进化算法中种群数设为100，迭代100次，模拟退火算法迭代600次，共迭代700次。混合算法优化试验收敛曲线如图4所示。

图4　差分进化与模拟退火结合算法收敛曲线

从图4可以看出，该算法在优化初期收敛速度极快，但是很快陷入收敛停滞，而优化后期搜解能力较强，利用更少的迭代次数就得到了比单纯模拟退火或者差分进化算法更好的优化结果。因此，该混合算法比差分进化与模拟退火算法的优化效率要高。

2　算法应用

本文采用该混合优化算法对一40×40的平面均匀阵列进行低副瓣优化设计。阵列单元呈矩形栅格排列，其中行间距dx=0.52 λ，列间距dy=0.52 λ，要求采用唯相位加权将副瓣优化到－20 dB以下。本文为更好地模拟实际阵列工作情况，取阵列单元方向图为cos(θ)，采用1.4节介绍的算法优化阵列副瓣。优化的方位面与俯仰面副瓣如图5所示。

图5　低副瓣优化方向图

从图5可以看出，经本文方法优化后阵列天线的方位面与俯仰面副瓣均达到了－22.13 dB，满足了设计目标。算例证明了该优化方法的有效性。

3　结束语

本文对唯相位加权实现天线低副瓣的问题进行了分析，通过总结差分进化算法与模拟退火算法的优化特点提出一种将两种算法结合起来的混合优化方法。计算结果表明，该算法在优化初期可以加快收敛速度，在优化后期可以增强搜解能力，从而使优化效率提高。采用该算法优化了40×40平面均匀阵列的副瓣，取得了较满意的结果。

参考文献:

［1］罗群，朱和平.相控阵天线手册［M］.北京:电子工业出版社，2007.

［2］闫秋飞，范国平，徐朝阳.一维唯相位低副瓣技术研究［J］.舰船电子对抗，2009，32(5):53-55.

［3］Yan K K，Lu Y.Sidelobe reduction in array-pattern synthesis using genetic algorithm［J］.IEEE Trans.on Antennas Propagat.，1997，45(7):1117-1122.

［4］Recioui A.Sidelobe level reduction in linear array pattern synthesis using particle swarm optimization ［J］.Jour.of Optimization Theory and Applic.，2012，15(3):497-512.

［5］Trucco A.Thinning and weighting of large planar arrays by simulated annealing［J］.IEEE Trans.on Ultrason.，Ferroelect.，Freq.Control，1999，46(2):347-355.

［6］Yikai Chen，ShiwenYang，Zaiping Nie.The application of a modified differential evolution strategy to some array pattern synthesis problems［J］.IEEE Trans.on Antennas Propagat.，2008，56(7): 1919-1927.

An antenna sidelobe reduction technology with phase-only weighting

CONG You-ji，BIAN Mei-qin，JIAN Lin
(No.724 Research Institute of CSIC，Nanjing 211153)

Abstract:With the analysis of the characteristics of some optimized array sidelobe algorithms，a phase-only weighting method combining the differential evolution(DE)algorithm and the simulated annealing(SA)algorithm is proposed and used to lower the array antenna sidelobe.Besides，in the process of optimization，the FFT is used to improve the efficiency of calculating the array antenna patterns.The array antenna sidelobe is up to－22.13 dB after the optimization of the phase-only weighting for 40×40 uniform arrays to prove the method to be effective.

Keywords:phase-only weighting; low sidelobe; array antenna

作者简介:丛友记(1986-)，男，工程师，硕士，研究方向:微波天线技术;卞美琴(1981-)，女，工程师，工程硕士，研究方向:雷达系统工程;简玲(1980-)，女，高级工程师，硕士，研究方向:微波技术。

收稿日期:2015-03-15;修回日期:2015-04-12

文章编号:1009－0401(2015)02－0045－04

文献标识码:A

中图分类号:TN820.13