型钢混凝土空间中节点受力性能有限元分析

王秋维，张月坤，张海镇

（西安建筑科技大学土木工程学院，陕西 西安 710055）

型钢混凝土结构具有承载能力高、抗震性能好和施工方便等优点，其在我国得到日益广泛的应用[1]．目前实际工程主要采用 I字型钢或核心十字型钢SRC柱，而此种传统配钢形式对核心混凝土的约束效果有限，SRC柱的抗震性能较普通钢筋混凝土柱提高不多[2-3]．在此背景下，作者在文献[4]中提出两种新型截面型钢混凝土柱，即正向布置和对角线布置扩大十字型钢SRC柱，试验研究表明，这两种新型柱的滞回曲线饱满，在高轴压比下具有比普通SRC柱更好的抗震性能[4]．

节点是连接梁和柱的关键部位，为保证节点的安全可靠，国内外对型钢混凝土梁柱平面节点进行了一些试验研究，如：薛建阳通过 15个框架节点的低周反复荷载试验，研究了混凝土异形柱框架节点的力学性能[5]；孙岩波对4个装配式框架节点进行低周反复加载试验，分析了节点的抗震性能[6]；Atsunori KITANO等通过偏心梁柱节点的低周往复荷载试验，发现偏心对SRC节点抗剪承载力的影响较小[7]．然而地震作用下，空间节点承受十字正交梁传来的双向弯矩、剪力和轴力的作用，节点内将产生复杂的受力状态和空间耦合作用，针对此情况，学者们开始对SRC空间节点的力学性能进行研究，例如：樊健生等通过方钢管混凝土柱-组合梁空间节点的抗震性能试验，研究加载路径对空间组合节点抗震性能的影响[8]；张士前等对型钢混凝土空间节点进行低周反复荷载试验，提出在斜向荷载作用下节点抗裂及抗剪承载力计算公式[9]．

与普通 SRC空间节点相比，当文献[4]中的新型SRC柱与SRC梁连接形成空间节点时，其受力机理和抗震性能尚不明确．因此，本文建立与平面节点对应的空间中节点有限元模型，研究SRC空间中节点在不同加载路径下的滞回性能、骨架曲线和延性性能，并进一步分析了楼板宽度、节点类型和轴压比等因素对中节点力学性能的影响．为该类节点的设计提供参考．

1 有限元模型建立

1.1 模型的构造方案

试件模型选取课题组已完成的5个SRC平面节点试件[10]：2个布置扩大十字型钢SRC柱-SRC梁节点试件(编号SSRCJ2和SSRCJ3)、2个对角线布置十字型钢SRC柱-SRC梁节点试件(编号SSRCJ4和SSRCJ5)和1个普通十字型钢SRC柱-SRC梁节点试件(编号SSRCJ1)，除试件SSRCJ3的梁与柱成斜交外，其它试件的梁与柱均为正交，梁柱型钢骨架连接构造如图1所示．

试验试件轴压比为0.40，型钢采用Q235钢，纵筋采用 4■20，箍筋采用 φ8@60(40)，试件外形尺寸、梁柱截面尺寸及配筋情况如图2所示，试件设计参数如表1所示．

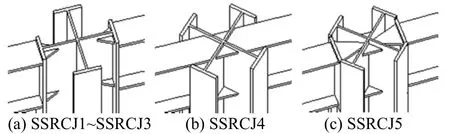
图1 型钢骨架连接示意图Fig.1 Connection diagram of steel skeleton

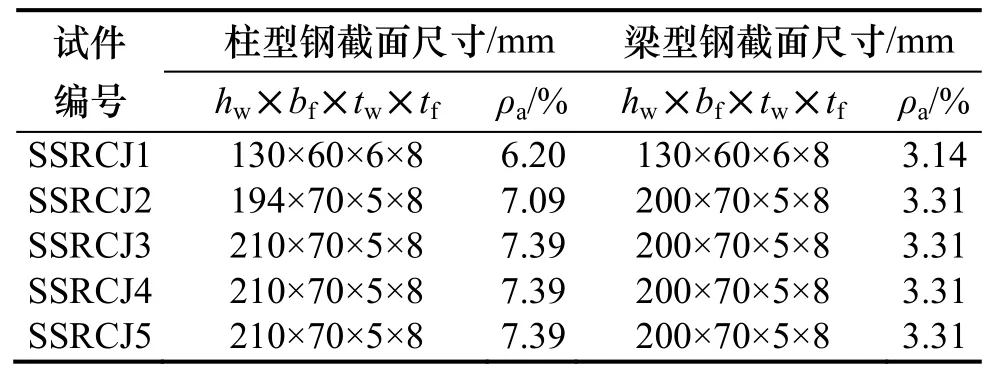
表1 试件设计参数Tab.1 Design parameters of specimens

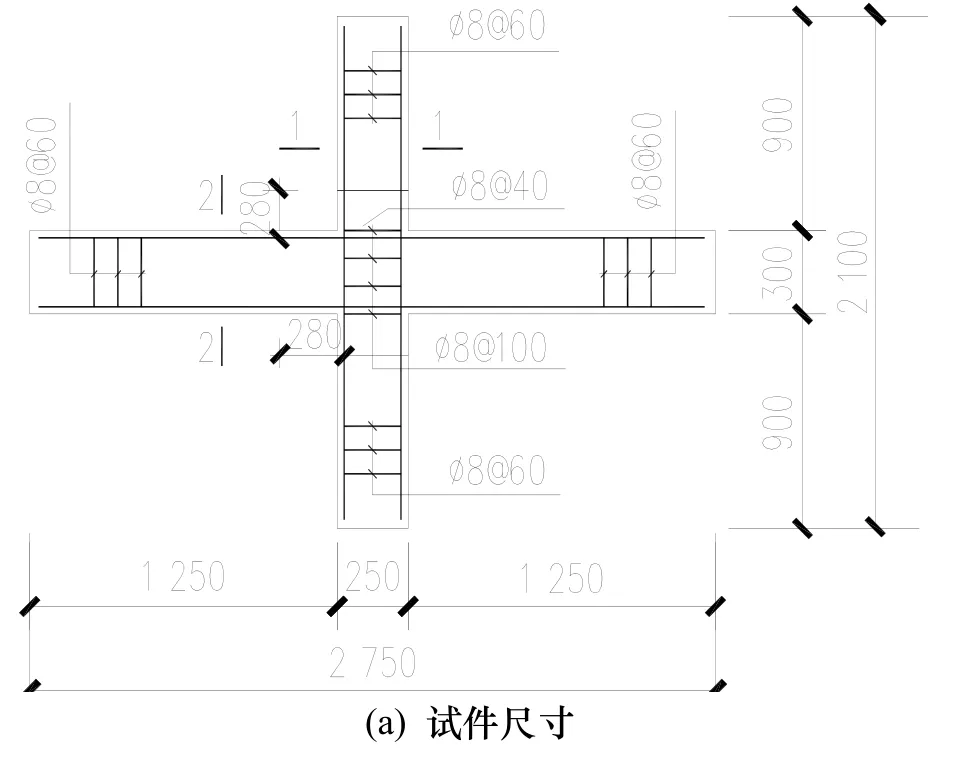
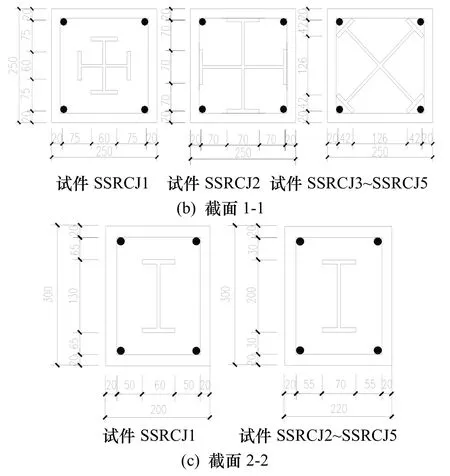
图2 试件截面形状及配筋Fig.2 Reinforcement arrangement and section shape of specimens

依据国家标准GB/T228.1-2010《金属材料拉伸试验第1部分：室温试验方法》[11]对钢材进行拉伸试验，测得其屈服强度和极限强度，实测数值均大于钢材的强度标准值．混凝土强度等级C50，保护层厚度20 mm，对试验前预留的6个边长为150 mm标准立方体试块进行强度测试，测得混凝土立方体抗压强度平均值为51.2 MPa．

1.2 材料本构模型

在 ABAQUS/Standard模块中，混凝土选用塑性损伤本构模型，要准确定义混凝土的塑性损伤本构模型，需要确定混凝土的屈服条件、混凝土应力-应变关系和损伤因子d：

(1) 屈服条件：膨胀角取30度，塑性流动势偏移值取 0.1，双轴极限抗压强度与单轴极限抗压强度的比值取1.16，拉压子午面上第二不变量取2/3，粘性系数0.005，混凝土受压恢复系数取0.8，混凝土受拉恢复系数取0.2．

(2) 混凝土的应力-应变关系：SRC空间中节点包含两种混凝土，型钢内的约束混凝土和型钢外的普通混凝土．约束混凝土采用韩林海教授提出的压应力-应变关系模型[12]，拉应力-应变关系和普通混凝土应力-应变关系按GB50010-2010《混凝土结构设计规范》[13]的规定选取．

(3) 模型通过引入损伤因子d，来模拟混凝土在往复荷载作用下的刚度退化，受压和受拉损伤因子dc、dt均采用文献[14]中的表达式．

1.3 单元类型及边界条件

混凝土和型钢均采用实体单元C3D8R，即8节点六面体线性减缩积分单元，原因是线性减缩积分单元对位移的求解结果较精确；钢筋采用T3D2单元，即2节点线性三维桁架单元．型钢与混凝土之间通过线性弹簧(springs)连接，钢筋和混凝土之间的相互作用设置为内置区域(embedded region)．同时在受力边界处和施加荷载处放置钢垫板，混凝土与垫板之间的相互作用设置为绑定(tie)．

为保证计算精度和合理的计算时间，经过试算网格单元划分为50 mm；模型中柱沿Z轴方向，梁沿Y轴方向，试件的柱底铰接，采用柱端往复位移加载来模拟试验中的加载方案．

2 有限元分析与试验结果对比

2.1 破坏形态

所有有限元分析试件均发生了核心区剪切破坏，与试验试件的破坏形态一致，如图3所示．以试件SSRCJ2为例说明，由图3(b)可知：加载初期，混凝土等效塑性应变的最大值出现在梁上，这与试验中裂缝首先出现在梁端的现象一致；随着水平位移的增大，混凝土等效塑性应变的最大值逐渐转移至节点核心区，试验中表现为节点核心区逐渐出现微裂缝；在破坏阶段，节点核心区混凝土等效塑性应变过大导致混凝土外鼓，而梁柱的等效塑性应变均较小，试验中表现为节点核心区混凝土已被压碎，而梁柱仅出现裂缝．

图3 试件破坏形态Fig.3 Failure mode of specimens

2.2 滞回曲线

通过有限元软件对新型 SRC梁柱平面节点的低周往复荷载试验进行模拟，并将模拟与试验的荷载(P)−位移(Δ)滞回曲线进行对比，如图4所示．由图可知：模拟所得滞回曲线与试验曲线吻合较好，两者的滞回环面积和循环次数基本一致，模拟中的不理想之处表现为滞回曲线的捏拢程度较差，分析原因是：模拟中型钢和混凝土之间通过线性弹簧连接，这不能很好地反映试验中它们之间的粘结滑移．有限元为单循环加载的原因：通过设置合理的损伤因子和粘结系数，来减小有限元与试验的误差，在保证精度的情况下，可以显著地减少模型的计算时间．

从上述分析可知，对于SRC梁柱平面节点而言，有限元模拟与试验结果较为一致，从而验证了有限元模型的有效性．

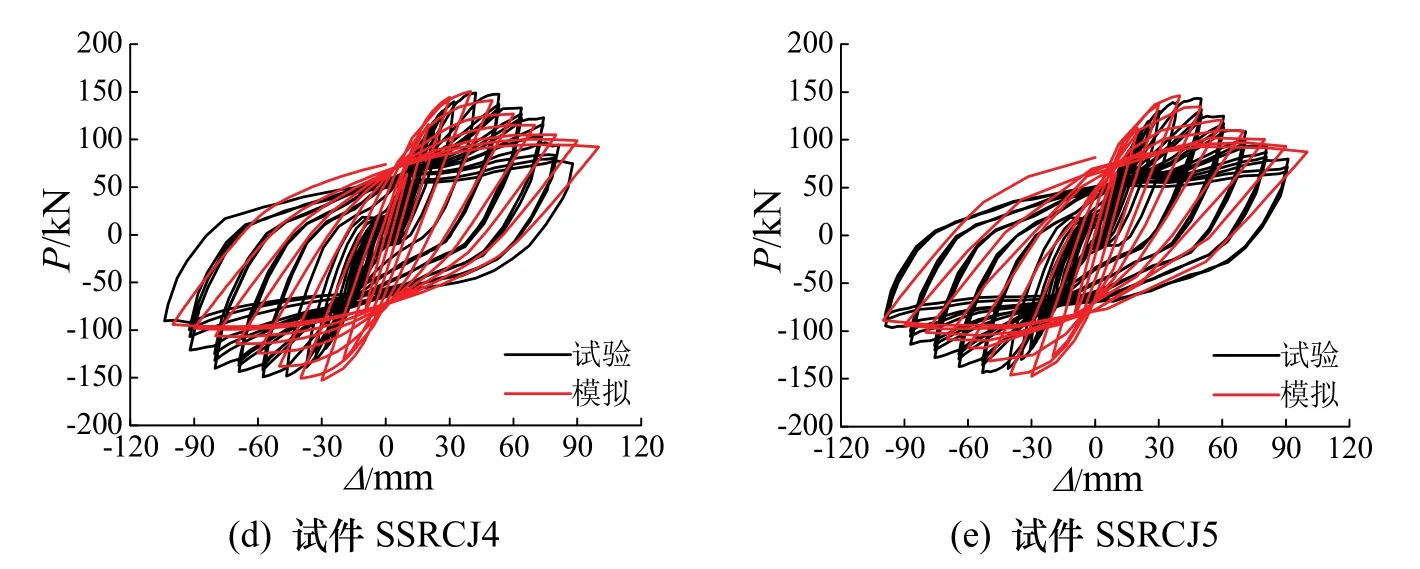
图4 模拟与试验滞回曲线对比Fig.4 Comparison between calculation and test results of hysteretic curves

3 加载路径对空间中节点力学性能的影响

在地震作用下，SRC空间节点将承受十字正交梁传来的双向弯矩、剪力和轴力的作用，节点内将产生复杂的受力状态和空间耦合作用，可见加载路径对节点的力学性能影响较大．在上述有限元验证的基础上设计SRC空间中节点，研究平面和两种空间加载路径对其力学性能的影响．

3.1 空间模型和加载路径设计

以1.1节SRC梁柱平面节点为基础，针对典型试件 SSRCJ1(代表柱内含普通十字型钢)、SSRCJ2(代表柱内含正向扩大十字型钢)和SSRCJ4(代表柱内对角线布置扩大十字型钢)设计空间中节点，对应的中节点编号分别为SSRCJ1-1、SSRCJ2-1和SSRCJ4-1，试件截面尺寸及配筋情况与平面节点相同(见表1和图2)，试件空间中节点模型如图5所示．

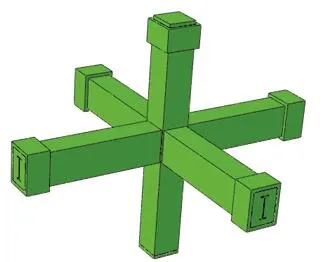
图5 空间中节点模型图Fig.5 Model of spacial interior joints

与SRC梁柱平面节点加载方式一样，SRC空间中节点也采用柱端加载方式，在此基础上设计 3种加载路径，分别为：

(1) 平面路径：首先在柱顶施加恒定轴向力，之后在柱端Y向施加往复位移直到试件承载力下降到极限荷载的80%～85%，位移增量取10 mm；(2) 空间路径 1：首先在柱顶施加恒定轴向力，之后在柱端X和Y向同时施加往复位移直到试件承载力下降到极限荷载的80%～85%，位移增量取10 mm；(3) 空间路径 2：首先在柱顶施加恒定轴向力，然后在柱端X向施加往复位移，位移增量取5 mm，之后在柱端Y向施加往复位移直到试件承载力下降到极限荷载的80%～85%，位移增量取10 mm．三种加载路径如图6所示．

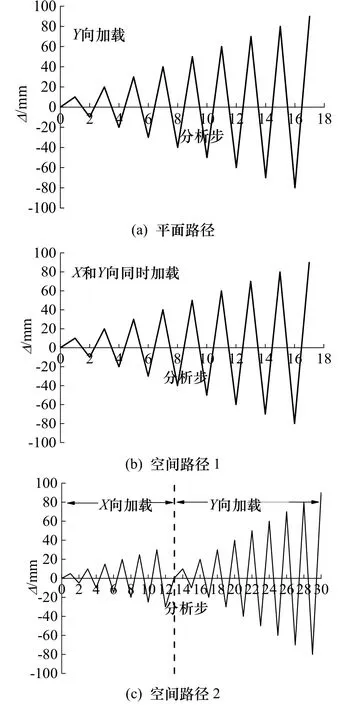
图6 加载路径Fig.6 Loading paths

3.2 破坏模式及受力机理分析

所有有限元试件均发生了核心区剪切破坏，将垂直X向的一根梁切除以显示中节点的核心区，如图7所示．以试件SSRCJ2-1为例，由图7(b)可知，加载初期，混凝土等效塑性应变的最大值出现在梁柱交汇处；随着水平位移的增大，混凝土等效塑性应变的最大值逐渐转移至节点核心区，柱型钢腹板逐渐屈服；在破坏阶段，节点的核心区均是灰色的，梁柱的等效塑性应变都很小，表明节点核心区混凝土已被压碎，柱型钢腹板全部屈服．

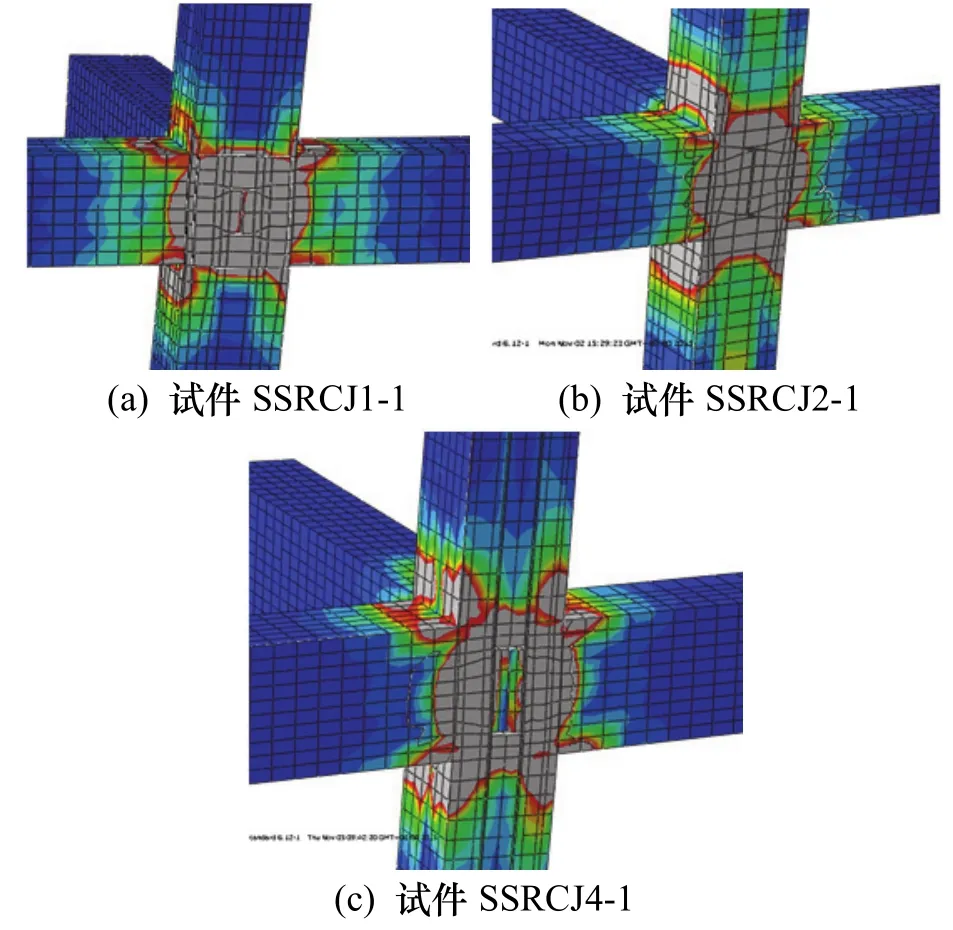
图7 试件破坏形态Fig.7 Failure mode of specimens

根据其受力过程及破坏形态，采用钢“框架-剪力墙”机理分析其抗剪承载力较为合理，即钢筋混凝土部分的抗剪可看作混凝土斜压杆加桁架来承担，型钢部分的抗剪可看作柱型钢翼缘构成的钢框架和柱型钢腹板作为剪力墙而组成的钢“框架-剪力墙”来承担．

3.3 滞回曲线

在不同的加载路径下，试件的滞回曲线如图 8所示，由图可知：

(1) 加载初期，滞回曲线呈线性增长，试件处于弹性状态；随着荷载的增加，试件进入弹塑性状态，加载曲线的斜率逐渐减小，表明试件出现累积损伤；峰值荷载后，曲线下降段平缓，表现出试件良好的变形能力．

(2) 与平面加载路径相比，节点在空间加载路径下的滞回曲线饱满程度较差，初始刚度和极限荷载较小，表明空间加载路径使节点核心区内产生双向耦合效应．

(3) 与试件SSRCJ1-1相比，试件SSRCJ2-1和SSRCJ4-1的滞回曲线更加饱满，且峰值荷载后曲线下降段更加平缓，表明柱内正向或对角线布置扩大十字型钢时，SRC空间中节点具有更好的承载能力和延性性能，分析原因是试件 SSRCJ2-1和SSRCJ4-1的核心区型钢约束的混凝土面积有所增大，进而提高了试件的力学性能．

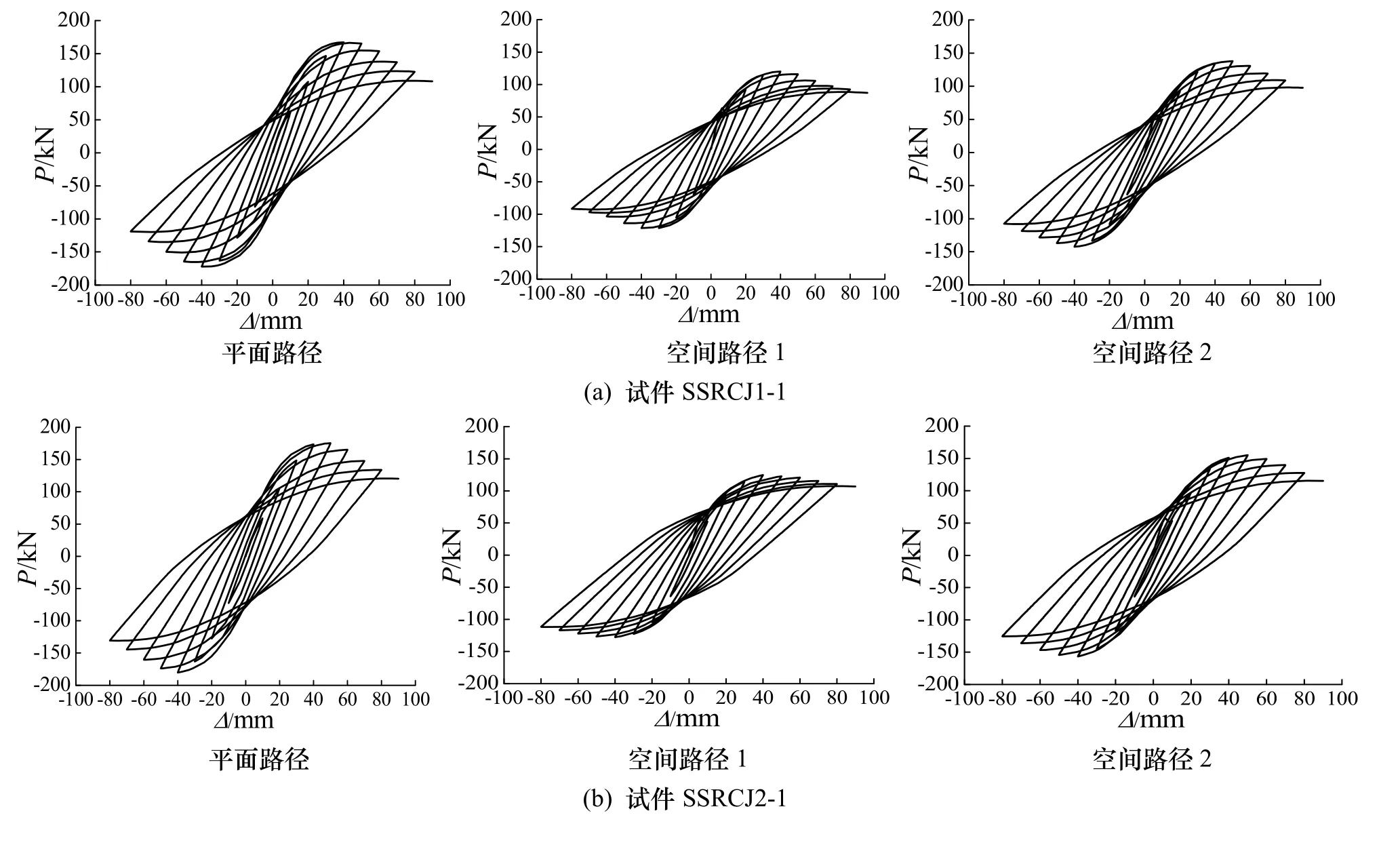
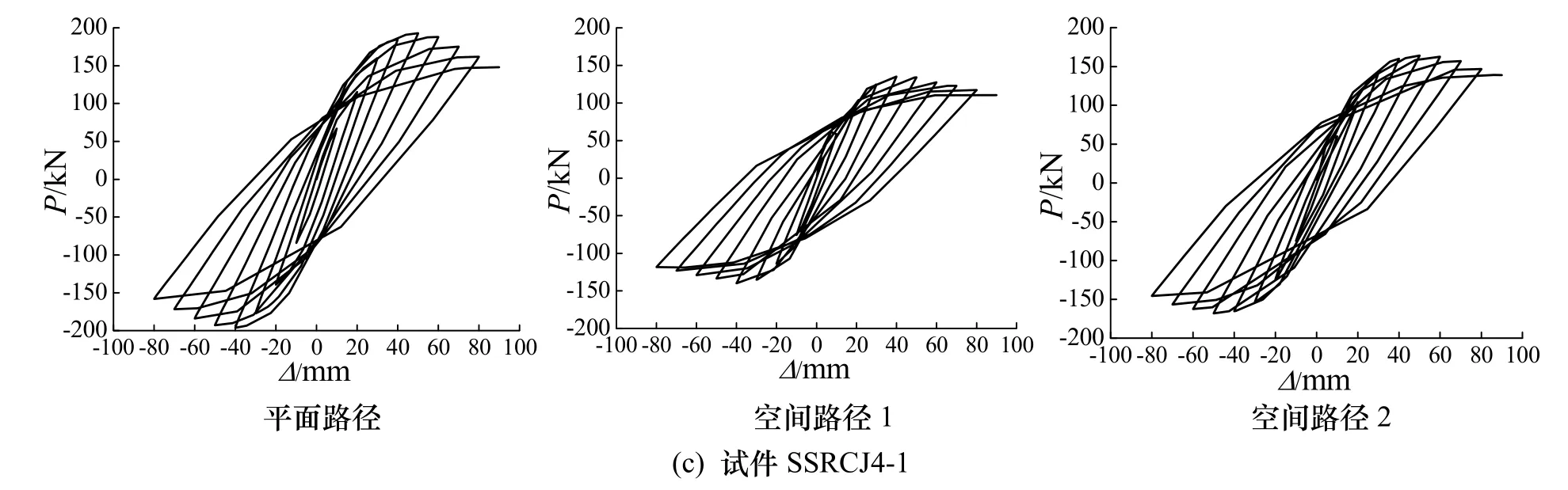
图8 不同加载路径下试件的滞回曲线Fig.8 Hysteretic performance of specimens under different loading paths

3.4 骨架曲线

试件的骨架曲线如图9所示．

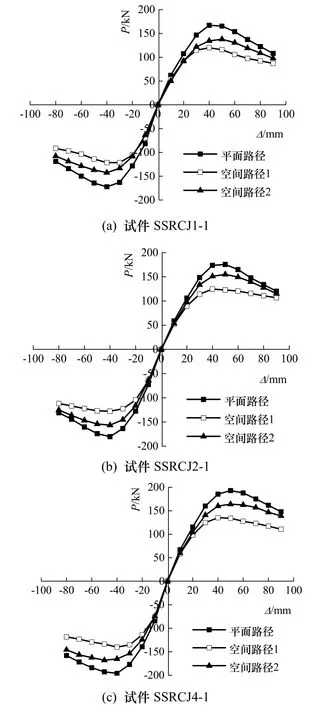
图9 试件的骨架曲线Fig.9 Skeleton curves of specimens

由图可知：(1) SRC空间中节点从开始加载到破坏经历了弹性阶段、弹塑性阶段和破坏阶段三个阶段．加载初期，骨架曲线基本为直线，试件处于弹性状态；随着荷载的增大，骨架曲线没有出现明显的拐点，试件的刚度逐渐退化，这是由于节点核心区的型钢和约束混凝土是逐渐屈服的；峰值荷载过后，试件的承载力缓慢下降，表现出良好的延性性能．(2) 加载路径对试件骨架曲线的弹性段影响较小，但对其屈服后的力学性能影响较大．与平面路径相比，SRC空间中节点在空间路径下的屈服荷载和极限荷载有所降低，其中在空间路径1作用下，节点的屈服荷载和极限荷载最小．可见，SRC空间中节点在空间路径下存在双向耦合效应；与空间路径2相比，空间路径1使节点内的双向耦合效应更加严重，这是因为X向加载引起节点核心区的损伤退化，导致Y向承载能力降低．

3.5 承载能力和延性性能

模拟所得试件的峰值荷载、屈服位移、极限位移和位移延性系数如表2所示，由表2可知：

(1) 与平面路径相比，在空间路径 1作用下，试件极限荷载和延性系数分别降低 30%和提高25%，在空间路径2作用下，变化程度分别为降低20%和提高15%，可见，空间加载路径导致节点核心区内产生双向耦合效应，从而降低了节点的承载能力，但其延性性能有一定的提高；在空间路径 1的作用下，节点内的双向耦合效应更加严重．

(2) 与试件SSRCJ1-1相比，试件SSRCJ2-1的极限荷载和延性性能分别提高 5%和 8%，试件SSRCJ4-1的提高程度则分别为13%和15%，可见，柱内正向或对角线布置扩大十字型钢时，空间节点的承载能力和延性性能较好，且对角线布置扩大十字型钢是一种更加优良的配钢形式．

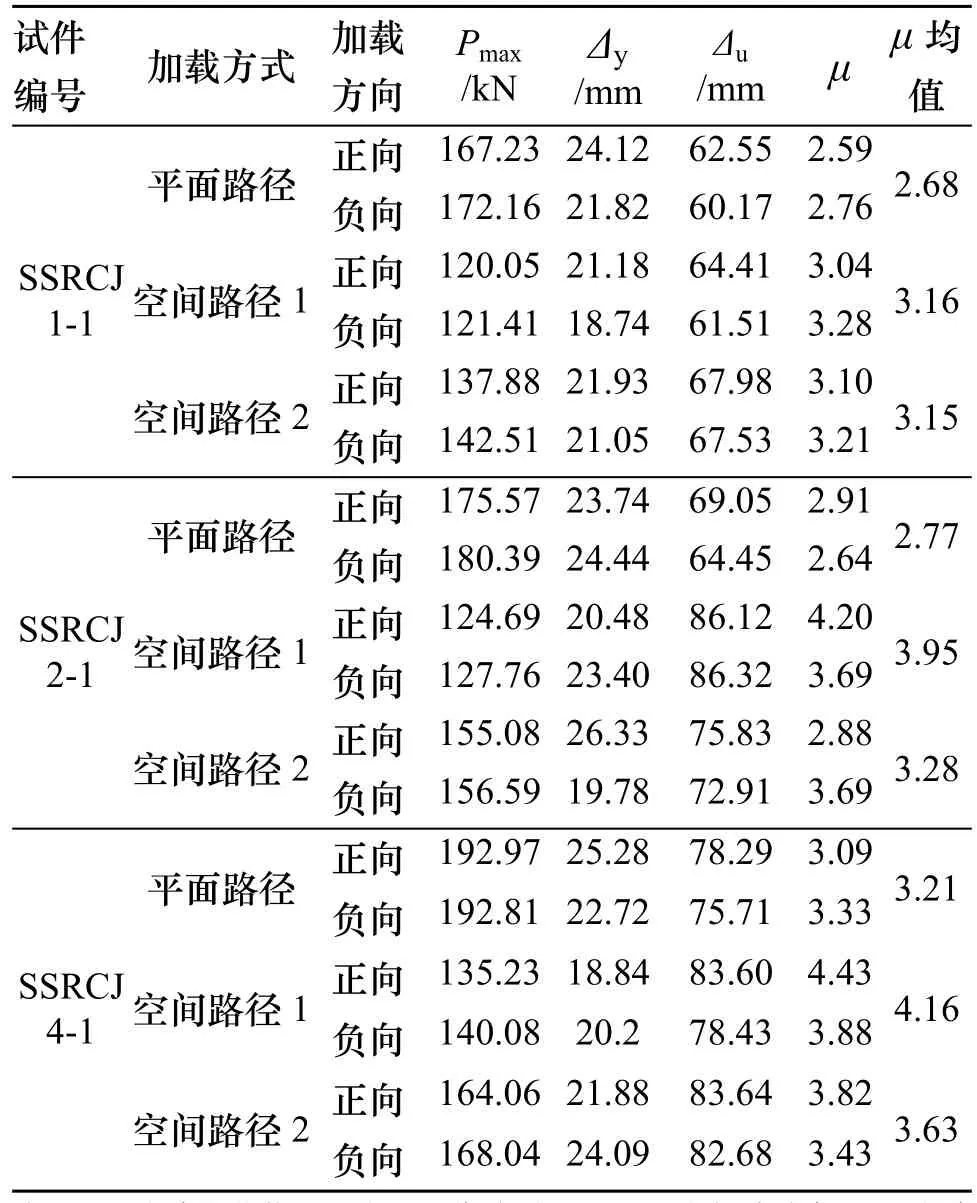
表2 试件承载力和延性Tab.2 Bearing capacity and ductility of specimens

4 不同因素对力学性能的影响

4.1 楼板

楼板有效翼缘宽度的取值方法主要有两种：GB50010-2010《混凝土结构设计规范》[13]中提出梁受压区有效翼缘宽度的取值方法和聂建国等提出梁负弯矩区有效翼缘宽度的计算公式[15]．

其它条件不变时，取SRC空间中节点的楼板板厚为60 mm(试验中采用1/2缩尺模型)，其中的分布钢筋为φ8@120，楼板宽度按上述两种方法计算并取整数，分别为900 mm、600 mm和无楼板．模拟计算所得的骨架曲线如图10所示．

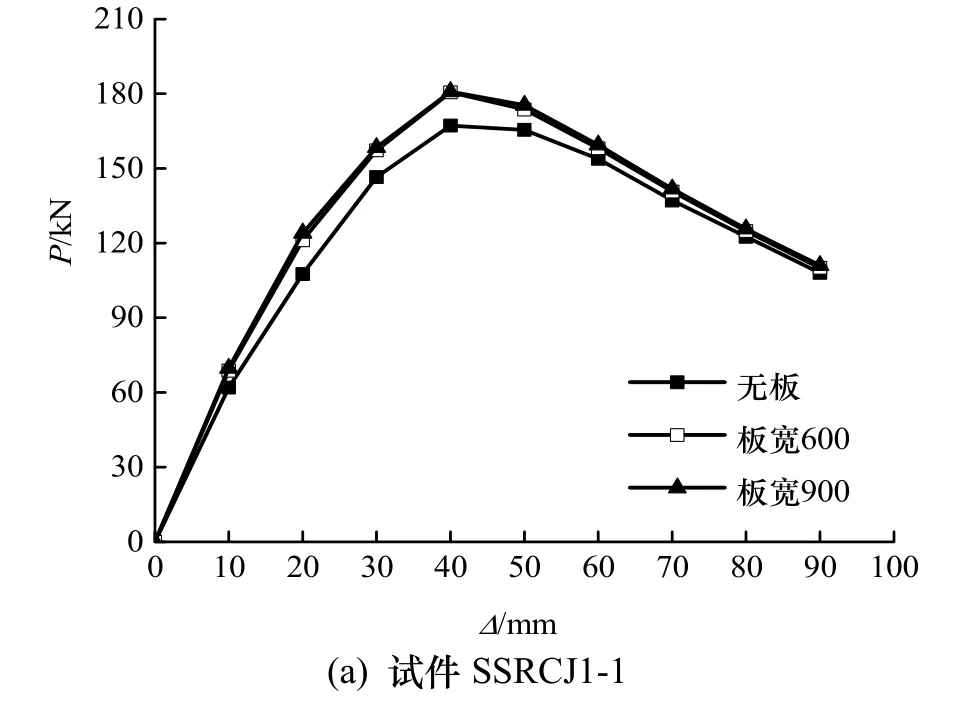
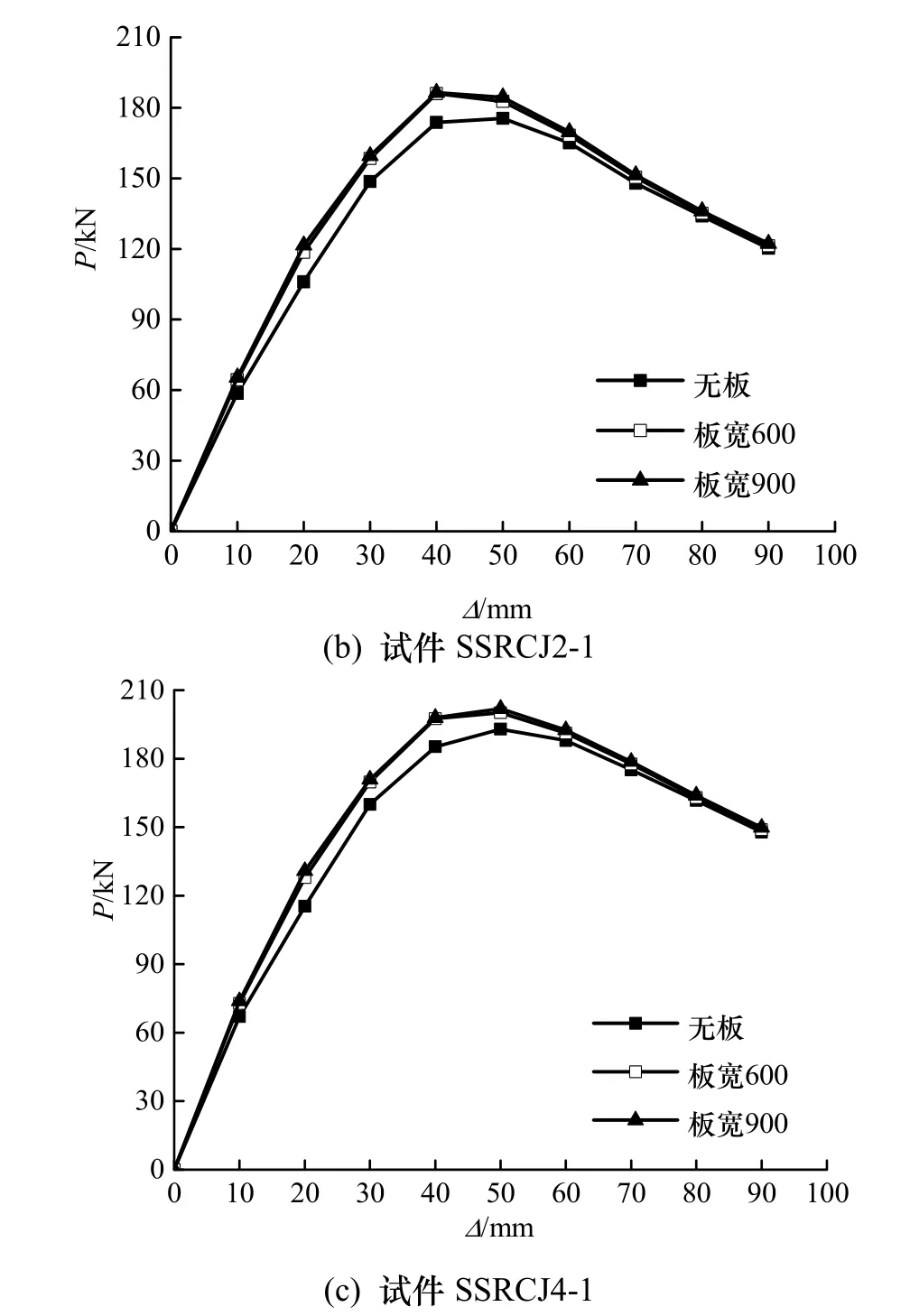
图10 楼板对节点骨架曲线的影响Fig.10 The effect of slabs on skeleton curves

由图可知：当楼板宽度取900 mm和600 mm时，试件的骨架曲线基本重合；与无楼板相比，楼板的存在使节点的初始刚度、屈服荷载和极限荷载稍有提高；楼板对试件骨架曲线的下降段影响较小．分析原因：(1) 对于强节点一般发生梁端弯曲破坏，此时楼板的存在增大了受压区面积，其极限荷载有较大提高，而对于本文设计的发生节点区剪切破坏的弱节点，楼板的存在对其极限荷载的影响很小；(2) 加载后期，楼板已经产生很大的裂缝，其对节点的约束效果变弱．可见，当SRC空间中节点发生剪切破坏时，楼板宽度对其承载能力和变形能力的影响较小．

4.2 节点类型

设计与 SRC空间中节点对应的空间边节点和角节点，其它条件相同时，模拟计算可得不同类型的SRC空间节点骨架曲线，如图11所示．

由图可知：(1) 加载初期，空间中节点和边节点的骨架曲线基本重合，表明在弹性状态，节点类型对试件骨架曲线的影响较小；(2) 与空间边节点相比，空间中节点的极限荷载有较大提高，这是因为空间中节点对核心区混凝土的约束效果更好；(3)与空间中节点和边节点相比，空间角节点的初始刚度、极限荷载和极限位移降低较多，分析原因是柱顶的水平位移在梁端产生的竖向力由原来两根梁承担变为由一根梁承担．

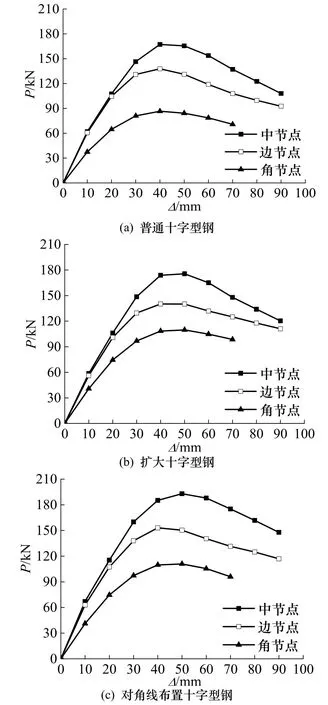
图11 节点类型对节点骨架曲线的影响Fig.11 The effect of joint types on skeleton curves

4.3 轴压比

其他条件相同时，模拟计算可得不同轴压比下(0.3、0.4和0.5)SRC空间中节点的骨架曲线，如图12所示．由图可知：(1) 在加载初期，三条骨架曲线基本重合，表明轴压比对骨架曲线的弹性阶段影响较小；(2) 随着轴压比的提高，峰值荷载变化较小，骨架曲线的下降段降幅逐渐增大，刚度退化加快，可见，随着轴压比的提高，SRC空间中节点的变形性能有所降低．

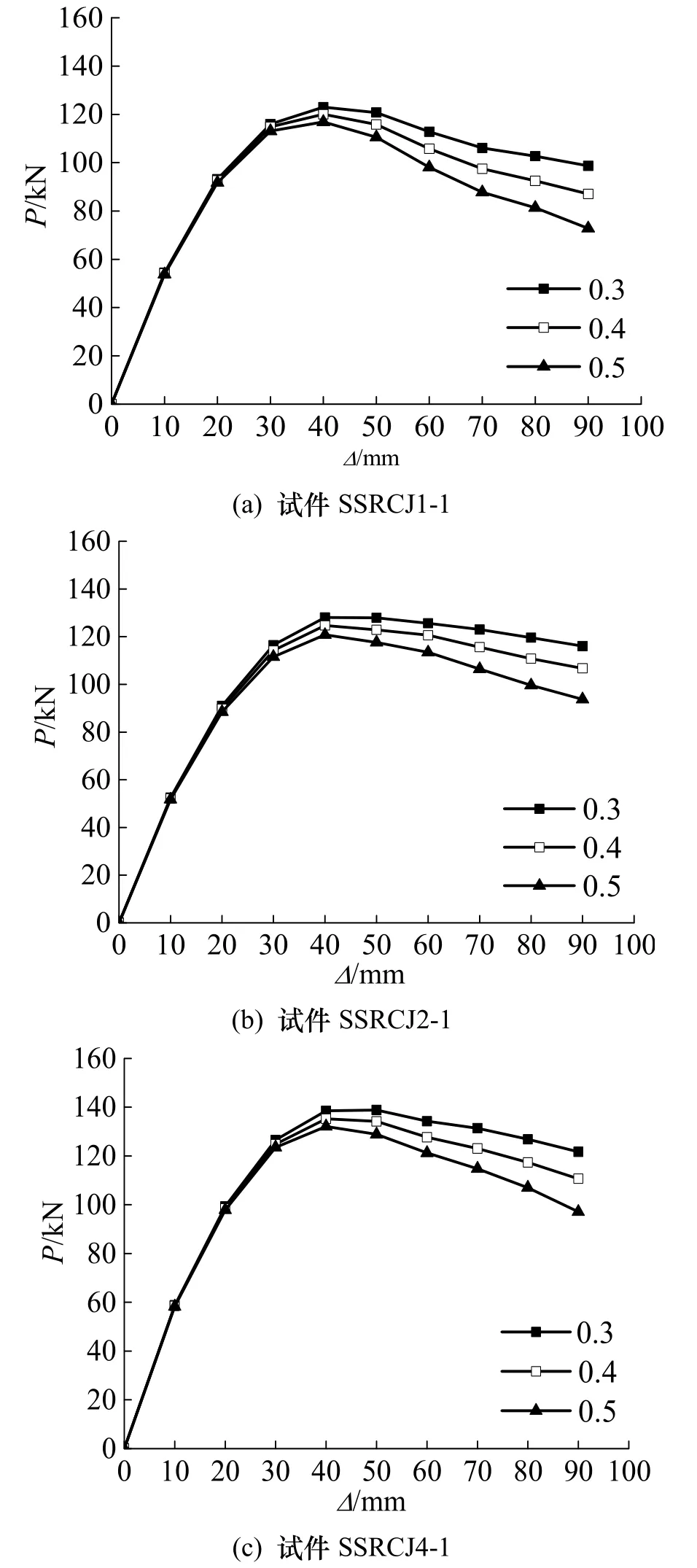
图12 轴压比对节点骨架曲线的影响Fig.12 The effect of axial compression radio on skeleton curves

5 结论

(1) 有限元模拟计算所得SRC梁柱平面节点的破坏形态、滞回曲线、骨架曲线和试验结果比较接近，因此，有限元程序 ABAQUS能够较好地模拟SRC梁柱平面节点在低周反复荷载作用下的力学性能．

(2) 加载路径对SRC空间中节点的力学性能影响较大，由于空间加载路径导致节点核心区内产生双向耦合效应，从而降低了节点的承载能力，但其延性性能有一定的提高；与空间路径2相比，空间路径1使节点内的双向耦合效应更加严重；与柱内配置普通十字型钢相比，柱内正向或对角线布置扩大十字型钢的承载能力和延性性能较好，且对角线布置扩大十字型钢是一种更加优良的配钢形式．

(3) SRC空间中节点发生剪切破坏时，楼板宽度对其承载能力和变形能力的影响较小；与空间中节点和边节点相比，空间角节点的初始刚度、极限荷载和极限位移降低较多；随着轴压比的提高，SRC空间中节点的变形性能有所降低．

References

[1] 韩林海, 陶忠, 王文达. 现代组合结构和混合结构[M].北京: 科学出版社, 2009.HAN Linhai, TAO Zhong, WANG Wenda. Modern composite structures and mixed structures [M]. Beijing:Science Press, 2009.

[2] 陈小刚, 牟在根, 张举兵, 等. 型钢混凝土柱抗震性能实验研究[J].北京科技大学学报,2009,31(12):1516-1524.CHEN Xiaogang, MU Zaigen, ZHANG Jubing, et al.Experimental study on the seismic behavior of steel reinforced concrete columns [J]. Journal of University of Science and Technology Beijing, 2009, 31(12):1516-1524.

[3] 刘阳, 郭子雄, 叶勇. 核心型钢混凝土柱抗震性能试验及数值模拟[J]. 华侨大学学报(自然科学版),2011,32(1): 72-76.LIU Yang, GUO Zixiong, YE Yong. Experimental investigation and nummerical simulation of seismic behavior of CSRC columns [J]. Journal of Huaqiao University(Natural Science), 2011, 32(1): 72-76.

[4] 王秋维, 史庆轩, 姜维山, 等. 新型截面型钢混凝土柱抗震性能试验研究[J].建筑结构学报,2013,34(11):123-129.WANG Qiuwei, SHI Qingxuan, JIANG Weishan, et al.Experimental study on seismic behavior of steel reinforced concrete columns with new-type cross sections [J].Journal of Building Structures, 2013, 34(11): 123-129.

[5] 薛建阳, 刘义, 赵鸿铁, 等. 型钢混凝土异形柱框架节点抗震性能试验研究[J].建筑结构学报,2009,30(4):69-77.XUE Jianyang, LIU Yi, ZHAO Hongtie, et al. Experimental study on seismic behavior of steel reinforced concrete special-shaped column-beam joints [J]. Journal of Building Structures, 2009, 30(4): 69-77.

[6] 孙岩波. 装配式型钢混凝土框架节点抗震性能试验研究[D]. 北京: 北京建筑大学, 2012.SUN Yanbo. Experimental Research on Precast Steel Reinforced Concrete Frame Joints [D]. Beijing: Beijing University of Civil Engineering and Architecture, 2012.

[7] KITANO Atsunori, GOTO Yasuaki, JOH Osamu. Experimental study on ultimate shear strength of interior beam-column joints of steel and reinforced concrete structure [C]//Proceedings of the 13thWorld Conference on Earthquake Engineering, Canada, 2004:626.

[8] 樊健生, 周慧, 聂建国, 等. 双向荷载作用下方钢管混凝土柱-组合梁空间节点抗震性能试验研究[J]. 建筑结构学报,2012,33(6): 50-58.FAN Jiansheng, ZHOU Hui, NIE Jianguo, et al. Research on seismic responses of 3D joints with CFT column and composite beam under bi-directional loading [J]. Journal of Building Structures, 2012, 33(6): 50-58.

[9] 张士前, 陈宗平, 王妮, 等. 型钢混凝土十形柱空间节点受剪机理及抗剪强度研究[J]. 土木工程学报, 2014,47(9): 84-93.ZHANG Shiqian, CHEN Zongping, WANG Ni, et al.Shear mechanism and shear strength of steel reinforced concrete(SRC) cross-shape 3D column-beam joints [J].China Civil Engineering Journal, 2014, 47(9): 84-93.

[10] 王秋维, 田贺贺, 史庆轩, 等. 扩大十字形截面型钢混凝土柱-SRC梁节点抗震承载力试验研究[J]. 建筑结构学报, 2015, 36(10): 96-104.WANG Qiuwei, TIAN Hehe, SHI Qingxuan, et al. Experimental study on seismic bearing capacity of steel reinforced concrete beam-column joints with enlarging cross-shaped section steel [J]. Journal of Building Structures, 2015, 36(10): 96-104.

[11] 中国国家标准化管理委员会. 金属材料拉伸试验第 1部分: 室温试验方法: GB/T228.1-2010 [S]. 北京: 中国标准出版社, 2010.Standardization Administration of the People's Republic of China. Metallic materials-tensile testing-Part 1: Method of test at room temperature: GB/T228.1-2010. [S].Beijing: Standards Press of China, 2010.

[12] 韩林海. 钢管混凝土结构-理论与实践 [M]. (第二版)北京: 科学出版社, 2007.HAN Linhai. Concrete filled steel tubular structure- theory and practice[M]. 2nd ed. Beijing: Science Press,2007.

[13] 中华人民共和国住房和城乡建设部. 混凝土结构设计规范: GB50010-2010[S]. 北京: 中国建筑工业出版社,2010.Ministry of Housing and Urban-Rural Construction of the People's Republic of China. Code for design of concrete structures: GB50010-2010[S]. Beijing: China Architecture＆Building Press, 2010.

[14] 李威. 圆钢管混凝土柱-钢梁外环板式框架节点抗震性能研究[D]. 北京: 清华大学, 2011.LI Wei. Study on the seismic performance of circular concrete-filled steel tubular column to steel beam joint with external diaphragm [D]. Beijing: Tsinghua University, 2011.

[15] 黄远, 聂建国, 易伟建. 钢-混凝土组合框架梁变形计算的有效翼缘宽度[J]. 土木工程学报, 2012,45(8):33-40.HUANG Yuan, NIE Jianguo, YI Weijian. Effective flange width for calculation of the deformation of steel-concrete composite frame beams[J]. China Civil Engineering Journal, 2012, 45(8): 33-40.