基于交叉亲和度评价的多种群遗传算法

王　东,归伟夏

(广西大学计算机与电子信息学院, 广西南宁530004)



基于交叉亲和度评价的多种群遗传算法

王东,归伟夏

(广西大学计算机与电子信息学院, 广西南宁530004)

摘要：为进一步解决传统多种群遗传算法进化过程中迅速丧失种群多样性，导致的易早熟、收敛到局部最优解等问题，提出一种基于交叉亲和度评价的多种群遗传算法，采用多种群并行搜索的思想，结合模拟退火算法提高算法的搜索能力，种群之间通过交叉推优选出的交流个体,进行亲和度评价替换目标种群个体来完成交流。通过对TSP问题的求解表明，算法得到的解都接近最优解，性能优于传统多种群遗传算法。

关键词:遗传算法；交叉亲和度评价；模拟退火；多种群

0引言

遗传算法(genetic algorithm，GA)是模拟达尔文的遗传选择和自然淘汰的生物进化过程的一种随机方法，由美国学者Holland教授[1-2]于1975年首次提出。由于GA在解决连续变量的函数优化问题中表现出来很好的鲁棒性、自适应性和隐含并行性，因此应用十分广泛[3-4]。然而遗传算法也存在很多问题，如计算代价太高，收敛速度缓慢，种群不能很好的覆盖搜索区域以及易陷入局部最优解等问题。

多种群并行遗传[5]是近年来所提出的改进遗传算法中性能较好的一种方法。其基本思想是用多个子种群代替原单一种群，使种群很好地覆盖搜索区域并使算法的搜索效率得到质的提高，每个子种群按不同的进化策略、遗传算子并行进化，并通过子种群间交换信息(一般为最优个体)来增加基因模式数，这样处理可以选取和保留每个子种群的优秀个体，在保持优秀个体进化稳定性的同时，加快进化速度，避免未成熟收敛。

目前关于多种群进化研究众多，如在搜索区域进行改进[6-7]，在遗传算子上做出改进[8]，还可以与其他搜索算法相结合，如王银年等[9]提出的改进模拟退火遗传算法，通过与模拟退火算法相结合，很好地提高算法的局部搜索能力。然而大多数学者在种群之间的交流上没有太多改进，通常的做法是将本种群中的最优个体直接替换其他种群中最差的个体，当种群规模不是很大时，由于外来优秀个体的进入，经过遗传操作迅速成为本种群的主导，使种群的多样性迅速下降，对于许多函数通常难以跳出局部最优解。本文针对此问题，提出一种交叉亲和度评价的交流算子，即选出种群之间要交流的个体后，通过交叉操作选出优秀子代，再进行亲和度评价替换目标种群中的个体，使种群在中后期仍然具有很好的多样性，避免陷入局部最优[10]。最后，通过对TSP问题的求解并与传统多种群遗传算法对比证明算法的有效性。

1基于交叉亲和度评价的多种群遗传算法

本文提出了一种基于交叉亲和度评价的多种群遗传算法，即AEMPGA，不仅在遗传算子方面做了改进，而且在种群的创建以及交流算子进行了优化。算法采用N加1种群模式，即N个子种群和一个最优保留种群，在每个子种群中，采用近邻法生成初始种群，并结合模拟退火算法构成近邻模拟退火遗传算法(NNSAGA)提高算法的局部搜索能力，在子种群之间交流采用交叉推优方式，进行亲和度评价操作，使种群的多样性得以提高。具体流程如图1所示。

图1　AEMPGA算法流程图

1.1　巡回旅行商问题

巡回旅行商问题[11](traveling salesman problem,TSP)，也称货郎担问题。简单来说就是给定n个城市和两两城市之间的距离，要求确定一条经过各城市当且仅当一次的最短路线。其图论描述为：给定图G(E，A)，其中E为顶点集,A为各顶点相互连接组成的边集，已知各顶点间的连接距离，要求确定一条长度最短的Hamilton回路，即遍历所有顶点当且仅当一次的最短回路。

以n=4为例，假设有四个城市A,B,C,D，四个城市连成一条回路的最短距离为B→A→D→C→B，则所走的距离为d=d(BA)+d(AD)+d(DC)+d(CB)。

1.2　近邻法

算法采用近邻法生成初始种群，以第一个城市为初始结点找出与其最近的城市作为后缀结点，第二个城市为初始结点找出与其最近的城市作为后缀结点，依照这样的做法找出每个城市的后缀结点，之后随机组合生成初始种群，这样做的好处是初始种群中的个体已经做了一定的优化，在寻优的开始就向好的方向发展，经过遗传操作可以迅速接近最优解。

1.3　模拟退火算法

模拟退火算法[12]( simulated annealing algorithm, SAA)于1983年成功地应用在组合优化的问题上。其思想是通过模拟高温物体退火过程的方法来找到优化问题最优或近似最优解的一种很强的局部搜索算法。模拟退火算法在搜索过程中具有概率突跳的能力，能够有效地避免搜索过程陷入局部极小解。模拟退火算法在退火过程中不但接受好的解，而且还以一定的概率接受差的解，同时这种概率受到温度参数的控制，其大小随温度的下降而减小。

求解过程如下：

①初始化退火温度Tk(令k=0)，产生随机初始解X0。

②在温度Tk下重复执行如下操作，直至达到温度Tk的平衡状态：

在解x的领域中产生新的可行解xo；

计算新解的评价函数f(xo)和旧解的评价函数f(x)的差值df；

依照概率min{1,exp(-df/Tk)}>random[0,1]接收新解，其中random[0,1]是[0,1]区间内的随机数。

③令Tk+1=ATk，k←k+1，其中A∈(0,1)。

若满足收敛判据，则退火过程结束；否则, 转②。

1.4　交叉推优选择交流个体

多种群中各子种群是相互独立的，种群间通过个体的交流来相互协调，交流个体是发挥多种群并行结构作用的关键因素，如果没有个体的交流，各种群间失去了联系则算法将等同于将多个不同控制参数标准遗传算法进行多次计算，从而失去了多种群的特色。传统的交流方式有两种：一种是将本种群中的最优个体直接替换其他种群中最差的个体，这种方式的优点是种群收敛速度快，缺点是当种群规模不是很大时，由于外来优秀个体的进入，经过遗传操作迅速成为本种群的主导，使种群的多样性迅速下降，对于许多函数通常难以跳出局部最优解；另一种方式是相邻种群之间随机挑出几个个体进行交叉，交叉后的子代替换原来两种群中最差的个体[13]。这种方法随机性较强，虽然使种群的多样性得以保持却没有将外来优秀基因带到本种群，这样对于全局的收敛性没起到很好的作用。

本文提出的算法将对此进行改进，采用单向环状拓扑，即将第i个种群的最优个体经交叉推优选出的子代迁到第i+1的种群中，第N个种群的最优个体经交叉推优选出的子代迁移到第1个种群中，其中i=1,2,…,N-1，N为种群个数。具体来说，首先找到本种群的最优解，之后找到目标种群的最差解，两个个体进行交叉操作，交叉后找出两个个体中较优的个体进行亲和度评价操作替换目标种群中的个体，这样做的好处是每次交流既带来外来优秀个体的部分基因又保留了目标种群个体的部分基因，使得外来优秀个体不会迅速成为主导，这样不仅带来了外来的优秀基因，而且使种群的多样性得以保持。

1.5　亲和度评价

经过交叉推优选出的交流个体携带源种群的信息进入到目标种群，增加了目标种群基因的模式数，在一定程度上补充了目标种群有可能缺失的有效基因。如果交流的个体与目标种群内已有的个体亲和度极大，即基因的相似度极大，则交流将毫无意义，有可能引起所有个体都趋向于同一状态，使得算法急剧收敛，丧失种群的多样性，因此进行一定的亲和度判断是有必要的，所以本文算法在个体交流过程中引入亲和度评价操作，在一定程度上避免这种情况。

1.5.1个体间亲和度计算

在遗传算法中，计算两个个体之间的亲和度时，可以认为每个基因就是一个特征分量，一条染色体就是其特征向量。所以个体间的亲和度可以用个体间的距离来计算[14],距离越大亲和度越小。

例如，某两个个体的染色体分别为X(x1,x2,…,xL)，Y(y1,y2,…,yL)，其中x，y表示组成该染色体的基因值，其中L表示个体染色体的长度。个体之间的差异为两个个体各个基因的距离求和，则第i个分量的距离计算方法如式(1)。

(1)

式中xi与yi为两个个体在第i位的基因值；maxi和mini分别代表第i位的最大基因值和最小基因值。对于二进制编码maxi=1；mini=0。如果xi=yi，dist(xi,yi)=0；否则，dist(xi,yi) = 1。

X、Y的亲和度计算如式(2)。

(2)

1.5.2替换操作

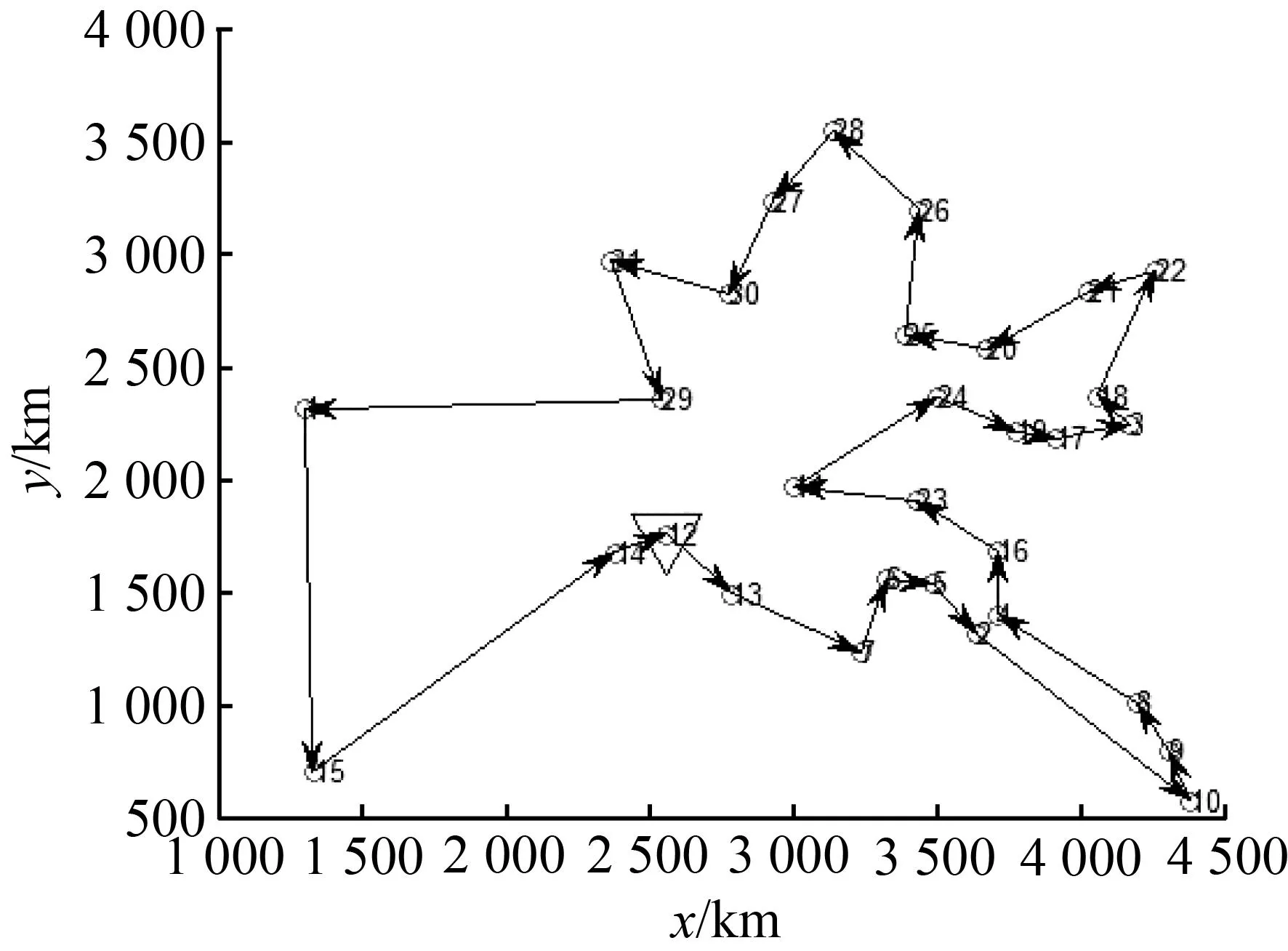
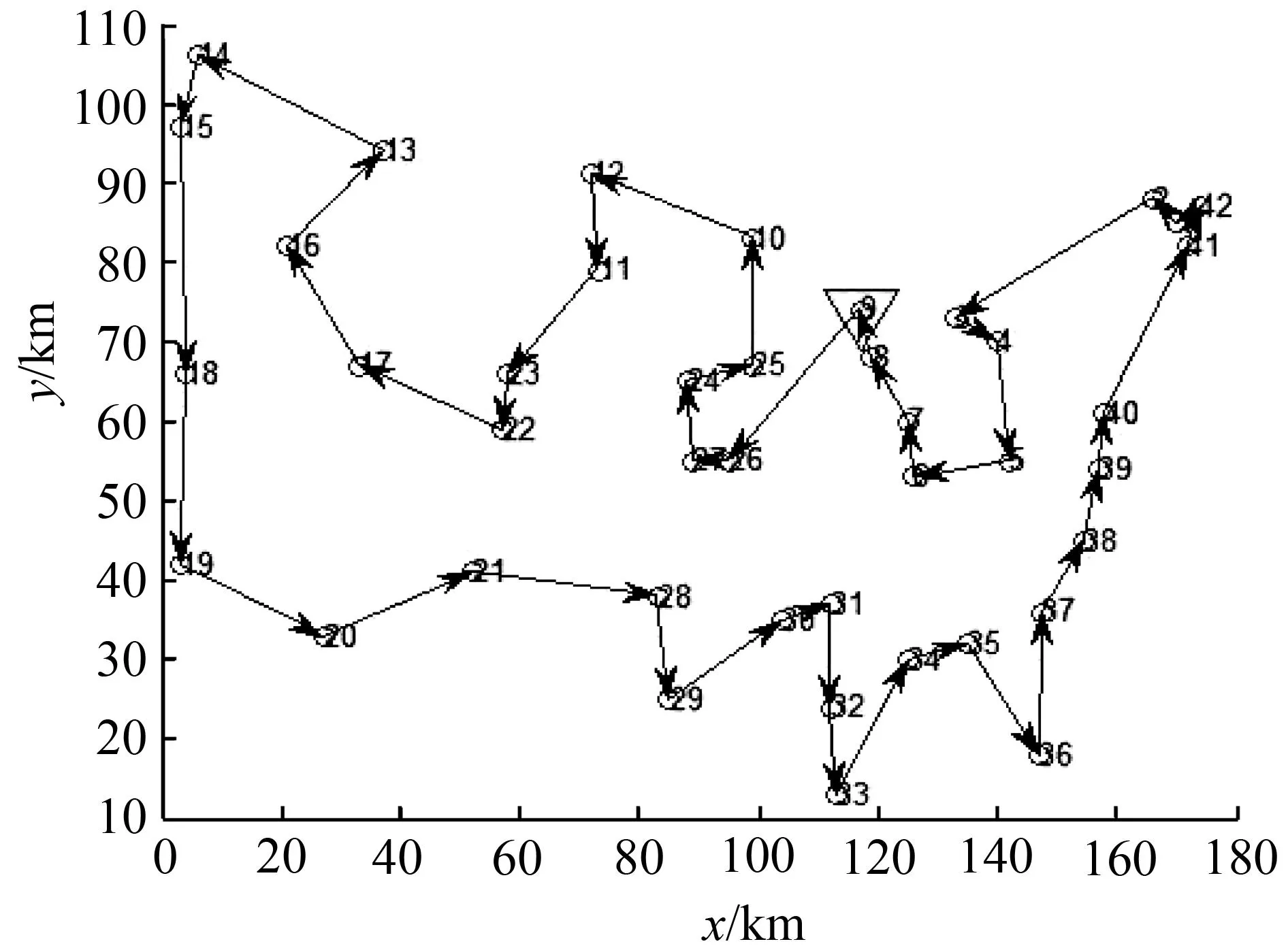
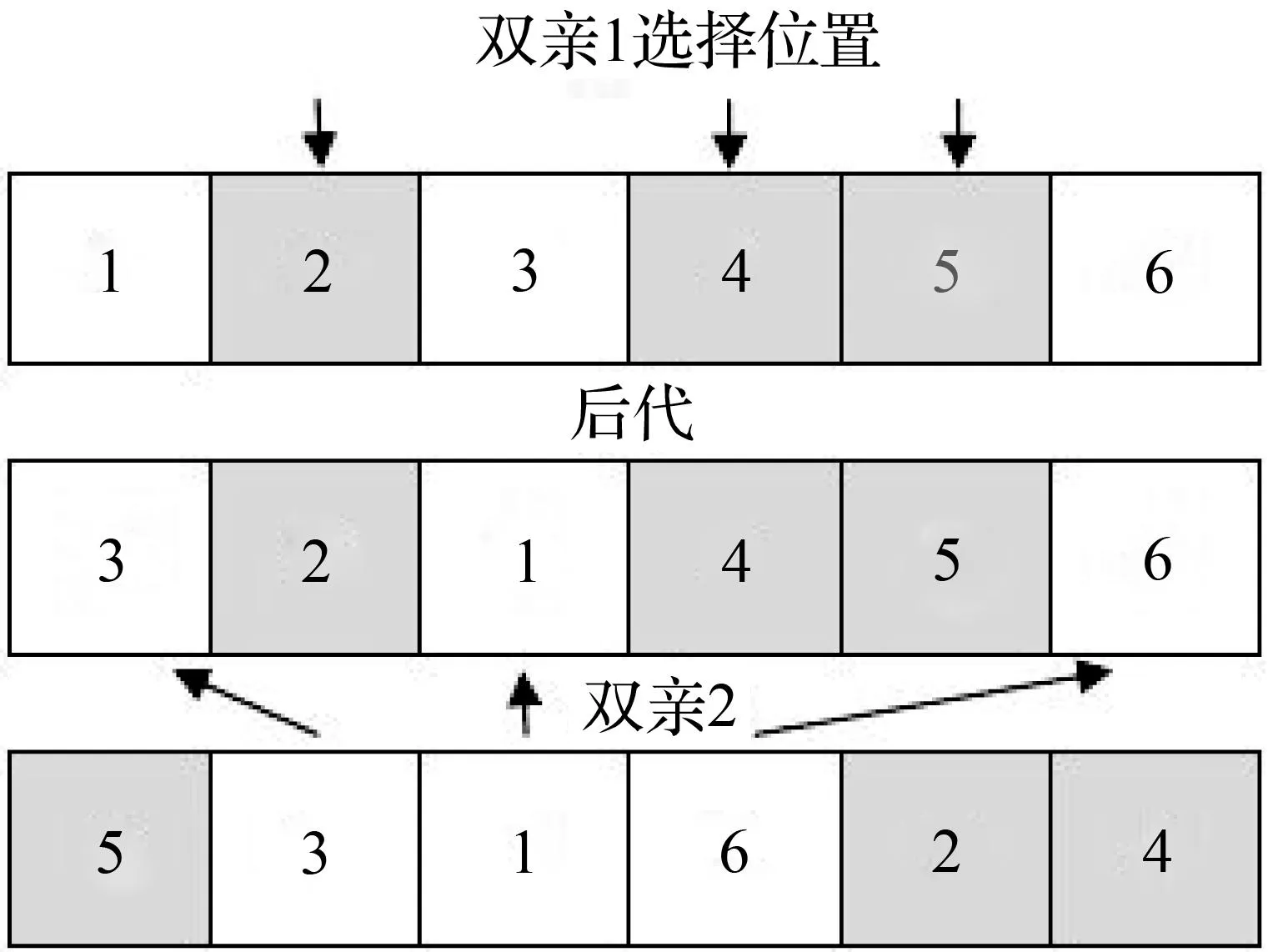
经过交叉推优选择出的交流个体与目标种群中的每一个个体进行亲和度评价，计算它们之间的acev(X,Y)，设置一个l，若两个个体的acev(X,Y)>=l，则认定这两个个体亲和度高，记录所有与交流个体亲和度高的个体，找出与交流个体亲和度最高的个体，如果交流个体的适应值大于与其亲和度最高的个体，则用交流个体替换与其亲和度最高的个体，否则用交流个体替换目标种群中适应值最小的个体。如果交流个体与任一评判成员的acev(X,Y)

2算法设计

2.1　编码(表达)

染色体通常采用简单的二进制串，但这种简单的表达方法不能较好地适用于TSP和其他组合优化问题。过去几年里，许多学者为TSP提出了几种染色体表达方法，其中，换位表达和随机键表达比较适用于TSP。本文算法采用换位表达。其中城市是按访问的顺序排列的，这种表达的搜索空间是城市顺序换位的集合，因此这种表达也称为路径表达或顺序表达。例如对于一个5城市的TSP：

5-2-1-3-4 可简单表示为[5 2 1 3 4]。

2.2　适应度函数

在TSP问题中，对于任意两个城市之间的距离D(i,j)已知，每个染色体(即n个城市的随机排列)可计算出总距离，因此本文算法将一个随机全排列的总距离的倒数作为适应度函数，即距离越短，适应度函数越高，因此满足TSP要求。

2.3　选择算子

传统的基本遗传算法中个体的选择概率与个体的适应值直接相关。一旦某个个体的适应值接近于0，则其选择概率将接近于0，这个个体产生后代的可能性就极低，这是基本遗传算法一个很大的缺点。因此本文算法采用顺序选择方法，顺序选择策略将选择概率固定化，其具体步骤为：

①按适应值大小对个体进行排序。

②定义最好个体的选择概率为q(根据实际问题设定)，这样每个个体都有可能被选中从而产生后代。

③根据轮盘赌策略确定用于交叉的双亲个体。

2.4　交叉算子

本文算法采用基于位置的交叉，它基本上是一种换位表达的均匀交叉加一个修复程序。

基于位置交叉的步骤：

①从一个双亲上随机地选一组位置；

②将这些位置复制到一个空字串的相应位置，产生一个原始后代；

③删去第二双亲上该组中已有的城市。剩下的城市构成了原始后代需要的顺序；

④按照这个城市顺序，从左到右将这些城市定位到后代空缺的位置上。

该步骤可用图2来说明。

图2　交叉操作步骤图Fig.2　Crossover operation steps

同理依据双亲1和双亲2可以确定出另一个后代[5 1 3 6 2 4]。

2.5　变异算子

本文算法的变异算子采用插入变异与反转变异相结合的混合变异算子。插入变异是随机选择一个城市，并将它插入到一个随机的位置中，反转变异是在染色体上随机地选择两点，将两点间的子串反转。

首先进行插入变异，之后进行反转变异，该步骤可用图3来说明。

图3　变异操作步骤图Fig.3　Mutation steps

2.6　最优保存

本文算法设有一个最优保留种群，用于存储记录最优个体，子种群每经过一代遗传操作就向最优保存种群提交找到的最优个体，最优种群将子种群提交的个体与历史存储记录作对比，如果优于历史记录的个体则予以替换，当所有子种群进行完以上操作后，从最优保留种群中选择出一个最优的个体作为全局最优解。

3算法步骤与仿真实验

3.1　算法步骤

Step 1: 确定种群规模NIND，种群个数MP，进化代数MAXGEN，交叉概率Pc，变异概率Pm,给定城市的坐标位置及个数X(i,j),模拟退火参数初始温度T0,终止温度Tend、退火参数k以及保存当前最优染色体Tmax。

Step 2: 依据“2.2”所述确定目标函数及其数学描述形式或量化方法。

Step 3: 采用近邻法产生具有代表性的初始种群，个体数目一定，每个个体表示染色体的基因编码。

Step 4: 计算个体的适应度，并判断是否符合优化准则，若符合，输出最佳个体及其代表的最优解，否则转向step 5。

Step 5: 采用顺序选择方法，依据“2.3”所述进行选择，确定出要进行交叉的个体。

Step 6: 交叉操作，采用基于位置的交换，依据“2.4”所述进行交叉操作。

Step 7: 变异操作，传统遗传算法采用单变异位算法，多变异位是选择多个位置进行变异操作每次选择都按照“2.5”所述选择。本文算法采用多变异位算法进行变异操作，这样做大大增加了种群的多样性。

通过自适应方法产生变异概率[15]：

(3)

式中，fmax为群体中最大的适应度值，favg为每代群体的平均适应度值，f为要变异的个体的适应度值。其中本文取Pm1=0.1，Pm2=0.01。如果群体最大适应值等于最小适应值，则只产生一个变异位，否则随机产生变异位的个数，再随机产生每次变异的位置，然后对选中个体进行变异。

Step 8: 模拟退火操作由经过遗传操作产生的新一代种群作为模拟退火的初始种群，依照“1.3”中第二点所述接受新解，温度下降。

Step 9: 交叉推优选择交流个体进行迁移操作，选择出每一个种群中的最优个体按照“1.4”中所述进行交叉推优操作并按“1.5”所述进行亲和度评价，选择交流个体进行迁移操作。

Step 10: 最优保存。按照“2.6”中所述进行最优保存。

Step 11: 终止判断。判断算法是否满足退火终止条件即低于最低温度，若满足，则终止算法并输出当前最优记录，否则令T=k×T，转step 4继续执行算法。

3.2　仿真实验

本文采用标准数据库Tsplib数据库中的5个数据集ulysses16、ulysses22、oliver30、chn31和dantzig42进行了算法的验证。(实验环境CPU Intel Core 2.67 GHZ，操作系统windows 7.0，编程工具matlabR2014a)

实验选取传统多种群遗传算法(MPGA)和模拟退火多种群遗传算法(SAMPGA)与本文算法进行对比，每个实验每个算法的平均值均进行100次求均值所得，Tbest为标准数据库给出的最优解，实验中模拟退火终止温度Tend都设为1。

实验1：ulysses16。

实验1参数设置如表1所示。

表1　实验1参数

1.此处无参数。

实验1结果对比如表2所示。

表2　实验1结果对比

实验2：ulysses22。

实验2参数设置如表3所示。

表3　实验2参数

1.此处无参数。

实验2结果对比如表4所示。

表4　实验2结果对比

实验3：oliver30。

实验3参数设置如表5所示。

表5　实验3参数

1.此处无参数。

实验3结果对比如表6所示。

表6　实验3结果对比

实验4：chn31。

实验4参数设置如表7所示。

表7　实验4参数

1.此处无参数。

实验4结果对比如表8所示，所得最优值路径如图4所示。

表8　实验4结果对比

实验5：dantzig42。

实验5参数设置如表9所示，所得最优值路径如图5所示。

表9　实验5参数

1.此处无参数。

实验5结果对比如表10所示。

表10　实验5结果对比

图4实验4所得最优值路径图

Fig.4The optimum path of experiment 4

图5实验5所得最优值路径图

Fig.5The optimum path of experiment 5

从以上实验结果可以看出，本文算法得到的解集中最优解与最差解之间的距离较小，即得到的解较为集中，且明显优于传统多种群遗传算法和模拟退火多种群遗传算法得到的解集，所得最优解都接近标准数据库给出的最优解，有些甚至等于或优于最优解。如实验4 chn31数据集，本文算法得到的最优解等于标准数据库给出的最优解15 377；实验5 dantzig42数据集，本文算法得到的最优解比标准数据库给出的最优解699低13.484 3，优于标准数据库给出的最优解。在城市数较少的时候，本文算法和传统多种群遗传算法都可以找到相同的最优解，而当城市数扩大时，本文算法找到的最优解都优于传统多种群遗传算法。从实验的参数设计可以看出，随着城市数的扩大，种群规模、种群数量、模拟退火的初始温度以及最大遗传代数都在同步提高。这是由于数据集增大导致数据量增大，增加种群的数量可以提高搜索的并行性以此提高算法的搜索效率，而种群规模、模拟退火的初始温度提高则扩大了搜索的范围。

4结语

本文通过分析传统多种群遗传算法存在易于早熟收敛的不足，设计出了一种改进的遗传算法AEMPGA，通过对TSP问题进行求解证明算法的有效性。与模拟退火算法相结合提高了算法的局部搜索能力，在种群的建立、遗传算子方面也做了许多改进，尤其是设计了新的基于交叉亲和度评价的交流方式，使交流更为有效，提高了种群的多样性。通过与其他多种群遗传算法对比，实验证明了本文算法的有效性。然而实验选取的数据量均为小型数据集，城市数较少，对于大规模数据，算法的效果不是很好，容易出现寻优时间过长等缺陷。因此在今后的研究中要针对大规模数据的问题设计更为理想的算法。

参考文献：

[1]ELANSARY A M, ELDAMATTY A A, NASSEF A O.A coupled finite element genetic algorithm technique for optimum design of steel conical tanks [J]. Thin-Walled Structures,2010,48(3):260-273.

[2]DEB K.An efficient constraint handing method for genetic algorithms[J]. Comput.Methods Appl.Mech.Engrg, 2000，186(24):311-338.

[3]李孝忠,任吉栋.改进的DNA遗传算法在指派问题中的应用[J]. 天津科技大学学报,2011,26(2):61-64.

[4]孙月峰,张胜红,王晓玲,等.基于混合遗传算法的区域大系统多目标水资源优化配置模型[J]. 系统工程理论与实践,2009,29(1):139-144.

[5]吕卉,周聪,邹娟,等.基于多种群进化的遗传算法[J]. 计算机工程与应用,2010,46 (28):57-60.

[6]刘守生,于盛林,丁勇,等.基于均匀分割的多种群并行遗传算法[J]. 数据采集与处理,2003,18(2):142-144.

[7]巩敦卫,孙晓燕.变搜索区域多种群遗传算法[J]. 控制理论与应用,2006,23(2):257-260.

[8]李鑫.改进变异操作的多种群遗传算法[J]. 信息系统工程,2012,20(9):136-140.

[9]王银年,葛洪伟.求解TSP问题的改进模拟退火遗传算法[J]. 计算机工程与应用,2010,46(5):44-47.

[10]CHANG W A, RAMAKRISHNA R S.A genetic algorithm for shortest path routing problem and the sizing of populations[J]. IEEE Trans on Evolutionary Computation,2002,6(6):566-579.

[11]马良.旅行推销员问题的算法综述[J]. 数学的实践与认识,2000,30(2):156-165.

[12]杨理云.用模拟退火算法求解旅行商问题[J]. 微电子学与计算机,2007,24(5):193-196.

[13]周松儒,归伟夏.一种基于免疫原理的多种群DNA遗传算法[J]. 广西大学学报:自然科学版,2013,38(5):1135-1139.

[14]李军华,黎明,袁丽华.遗传算法求解TSP的种群多样性研究[J]. 小型微型计算机机系统,2008,29(3):544-547.

[15]SCINVIVAS M, PATNAIK L M.Adaptive probabilities of crossover and mutation in genetic algorithms[J]. IEEE Trans SMC, 1994, 24(4):656-666.

(责任编辑梁碧芬)

A multi-population genetic algorithm based on cross accessibility evaluation

WANG Dong， GUI Wei-xia

(College of Computer, Electronics and Information, Guangxi University, Nanning 530004, China)

Abstract:To solve traditional multiple population genetic algorithm for rapid loss of species diversity in the process of evolution, which may result in easy premature convergence to local optimal solution, a multiple population genetic algorithm based on cross accessibility evaluation is put forward. By adopting the idea of parallel search multiple species, it combines with the simulated annealing algorithm to improve the search ability.The individualis elected by crossover excellent recommendation among multiple populations and the target population is replaced through evaluating accessibility to complete communication. Finally, the algorithm is used to solve the TSP problem. The results show that the solution is close to the optimal solution and the performance is superior to traditional multiple population genetic algorithm.

Key words:genetic algorithms; cross accessibility evaluation; simulated annealing; multi-population

中图分类号：TP18

文献标识码：A

文章编号：1001-7445(2015)06-1508-09

doi:10.13624/j.cnki.issn.1001-7445.2015.1508

通讯作者：归伟夏(1974—),女,广西南宁人,广西大学副教授,博士;E-mail:740473@qq.com。

基金项目：国家自然科学基金资助项目(61363002);广西教育厅科研基金资助项目(LX2014002)

收稿日期：2015-09-01；

修订日期：2015-10-01