基于几何法的动力学定轨方法研究

2016-01-20孙江艳

全球定位系统 2015年2期

关键词：动力学

周　田,张　辉,孙江艳,李　博

(北京卫星导航中心,北京 100094)

基于几何法的动力学定轨方法研究

周田,张辉,孙江艳,李博

(北京卫星导航中心,北京 100094)

摘要：几何定轨方法不受力学模型误差的影响,过程简单,但是定轨精度不高,轨道外推精度也得不到保证。动力法定轨精度较高,但是在完成观测数据积累之前无法定轨,并且受到力学模型精度的影响。本文结合几何法和动力法的优点,研究了基于几何法的动力学定轨方法,仿真结果表明：该方法可以得到优于几何法的定轨结果,并且结果比较稳定。

关键词：几何法;动力学;定轨

doi:10.13442/j.gnss.1008-9268.2015.02.013

中图分类号：P228.4

文献标志码：A

文章编号：： 1008-9268(2015)02-0058-04

收稿日期：2014-09-03

作者简介

Abstract:Geometric orbit determination method is not a mechanical model error, the process is simple, but the orbit determination accuracy is not high, the track extrapolation accuracy can not be guaranteed. Dynamic orbit determination accuracy is high, but unable to orbit determination, and before the completion of the observational data accumulated by the mechanical accuracy of the model. In this paper, the advantages of the geometric method and dynamic method to study the orbit determination based on the geometric method of dynamics simulation results show that this method can be better than the geometric method of orbit determination results, and the results are relatively stable.

0引言

几何法定轨不受力学模型误差的影响,定轨过程相对简单,可以实时确定卫星位置,但是定轨精度不高,由于不涉及卫星的动力学性质,轨道外推的精度也不能保证。几何法定轨得到的轨道是一组离散的点,连续的轨道必须通过拟合方法给出,影响几何法定轨精度的主要因素是观测量的精度、参考站分布的几何构形;动力法定轨精度较高,能够得到卫星位置和速度信息,但是在完成观测数据积累之前,无法提供定轨结果,动力法定轨精度易受力学模型精度的影响[1-2]。在轨道恢复期间,可以采用几何法提供可靠的轨道,但是几何法精度不高,观测中断情况下不能得到轨道信息。在轨道回复期动力学模型已经稳定,结合动力平滑的思想,综合几何法和动力法的优点,采用基于几何法的动力学方法,该方法是以几何法定轨结果作为观测量的动力学定轨方法,实际上是一种几何动力学法,利用动力学方程约束几何法轨迹,对几何法结果进行平滑,减少了随机误差,获得了精度高于几何法的实时定轨结果,结果更加稳定[3-4]。

1基本原理

基于几何法的动力学定轨其核心算法是采用带轨道动力学模型的卡尔曼滤波器,对观测数据进行序贯分析[5]。其主要特点是不需要积累大量的观测数据,而是通过轨道动力学模型对卡尔曼滤波器的状态量进行时间更新和导航系统的测量数据对状态量进行测量更新,从而实现对状态量的不断修正,使定轨结果不断收敛直到稳定,这里的观测量指的是几何法定轨的结果。

卡尔曼滤波是一种基于物体运动状态参数的变化描述物体运动的参数估计方法。在确定了系统的初始状态后,应用卡尔曼滤波对状态向量进行估计时,不需要存储大量的历史观测数据,只需要根据滤波方程及新的观测向量即可求得新的状态向量滤波值,大大减少了信息的存储量及计算量,所以卡尔曼滤波被广泛应用于动态测量系统中[6-7]。

采用卡尔曼滤波对观测数据的噪声进行参数估计,在先验的模型误差矩阵辅助下,有效的滤除了高斯白噪声,提高了定轨的精度;引入了轨道动力学模型,当状态参数收敛到稳定状态后,其短时间的外推,能够保证较高的精度,实现了定轨结果的连续性;通过对观测数据中的粗差检测与剔除机制,避免了粗差对状态量的干扰,实现了定轨结果的稳定性。

2动力模型

主要介绍基于几何法的动力学定轨中考虑的摄动力、相应的运动方程及积分方法。

为了提高定轨的精度,动力学信息考虑的越全面越好。但是,为了保证处理的速度,考虑的摄动力又不能太过复杂。同时考虑定轨的精度和处理的速度,在基于几何法的动力学定轨中,考虑了如下的力模型:10×10阶地球引力、月球引力和太阳引力。在这样的力模型条件下,不会引入其他的待估力学参数,可以保证处理的实时性,并能够满足处理过程对力学模型精度的要求。

联系人：周田 E-mail: yuxiaoyanzhoutian@163.com

在考虑以上摄动力条件下,卫星的加速度为

(1)

式中: r(t)表示t时刻卫星在惯性系下的加速度矢量; re表示10×10阶地球引力加速度,其计算方法见相关参考文献; rs,rm表示日月引力加速度,计算方法见相关参考文献。

3观测模型

将在t时刻通过几何法得到的卫星位置作为观测向量(卫星在地固系下的位置)转换到惯性坐标系中,用Y(t)表示,观测方程可以表示为

Y(t)=h(X(t),t)+v(t),

(2)

式中: X(t)为t时刻卫星在惯性系下的状态向量,为待估量;h(X(t),t)为t时刻状态向量X(t)对应的真值; v(t)为t时刻的观测误差。对观测方程线性化得

Y(t)=HX(t)+v(t)，

(3)

式中: H为观测向量与待估向量之间的关系矩阵,

4参数估计

参数估计的方法有两种,一种是批处理算法,另一种是序贯处理算法。与批处理的算法相比,序贯处理算法具有以下两个特点[8]。

1) 接收到一个新的观测数据后,马上可以处理以得到观测时刻的新的状态估值。它的实时性强。

2) 序贯处理算法可以避免大维数矩阵的求逆运算。

采用的扩展卡尔曼滤波(EKF)就是一种序贯处理方法。扩展卡尔曼滤波在对非线性模型应用泰勒公式进行线性化,选用滤波估值作为标称值,这样就可以克服模型线性化引起的误差[9-10]。

EKF处理过程主要包括时间更新和量测更新两部分。给定先验协方差矩阵Pk-1以及初始轨道Xk-1,读取tk时刻的观测向量Yk,以及观测误差协方差阵Rk.式(4)和式(5)为时间更新部分,式(6)、式(7)和式(8)为量测更新部分。

(4)

(5)

(6)

(7)

Pk=(1-KkH)Pk/k-1.

(8)

使用卡尔曼滤波的一个基本前提条件是给定初始状态向量的估值X0和协方差阵P0.卫星位置直接从几何法定轨中得到,卫星速度可由两个历元的位置计算得到,协方差阵根据几何法定轨精度给定。

为了保证数据的稳定性,选择3倍观测中误差(即几何法定轨获得的卫星位置中误差)作为限值,若几何法得到的卫星位置与该时刻卫星的状态预报值的残差大于3倍观测中误差,则不进行量测更新,即剔除这个值。

扩展卡尔曼滤波算法的计算流程如图1所示。

图1　扩展卡尔曼滤波算法流程

5基于几何法的动力学定轨结果分析

为了便于分析,选取PRN23卫星6个站的情况、2011年1月27日 16:25:00-16:55:00共30分钟1s采样间隔的数据,进行基于几何法的动力学定轨,对定轨的结果与几何法进行对比。其中离散点表示几何法定轨的结果,红线表示基于几何法的动力学定轨的结果。图2(a)中纵坐标dR、dT、dN和dP分别表示R方向、T方向、N方向和三维位置的误差,图2(b)中纵坐标dVx、dVy、dVz和dV分别表位X方向、Y方向、Z方向和三维速度的误差。

从图2可以看出,基于几何法的动力学结果较几何法有了较大的改进,而且可以获得卫星的速度。在处理一段时间以后,滤波逐渐收敛,精度也趋于稳定。

表1和表2示出了收敛后的卫星位置和速度误差情况。

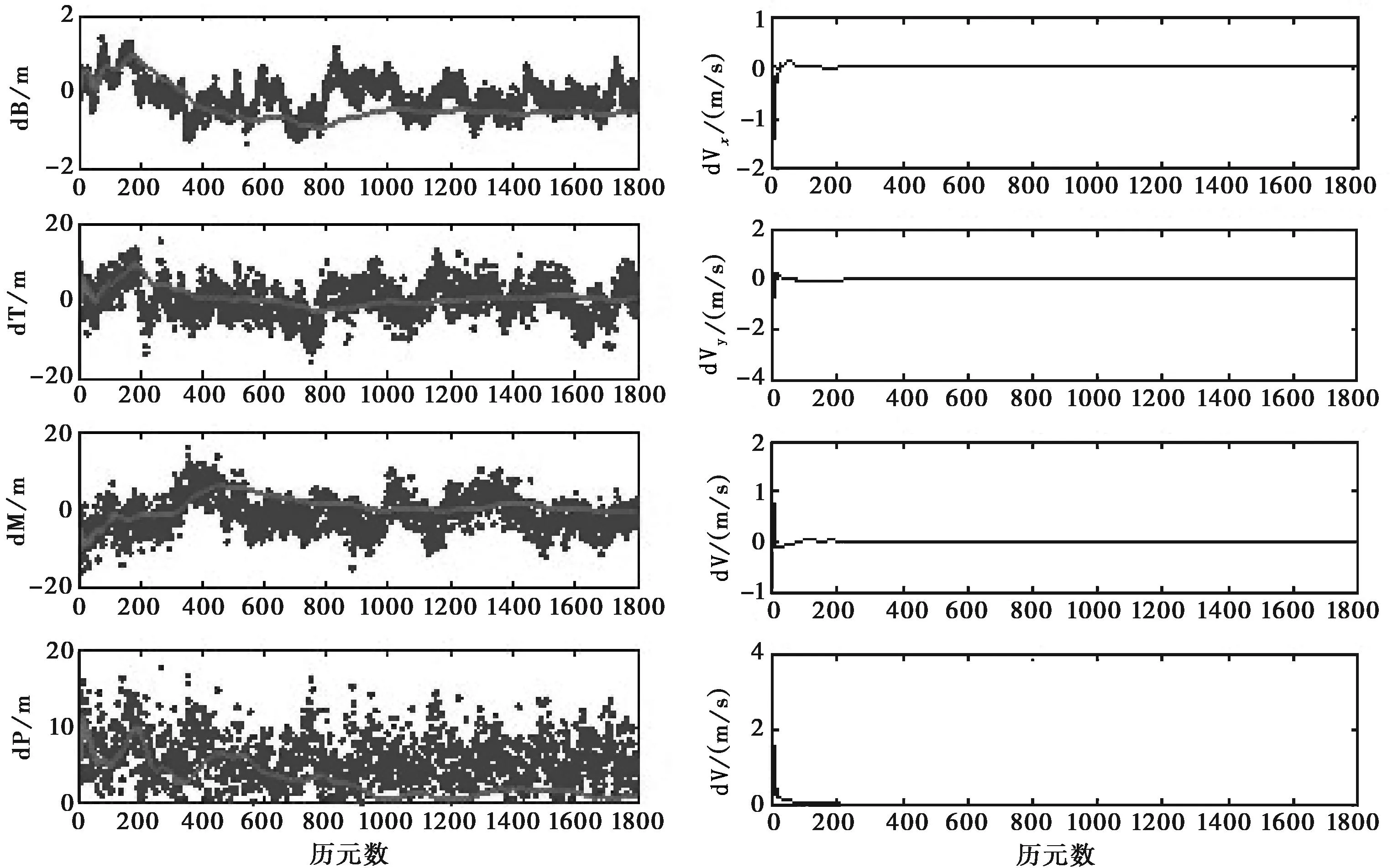
图2　基于几何法的动力学定轨结果

表1　收敛后卫星位置误差统计表 (单位：m)

表2　收敛后卫星速度误差统计表 (单位：cm/s)

从表1和表2可以看出,基于几何法的动力学定轨收敛后,卫星三维位置误差的平均值为1.647 m,标准差为0.953 m,而几何法定轨三维位置误差的平均值为5.546 m,标准差为2.872 m.三维速度误差的平均值为0.492 cm/s,标准差为0.344 cm/s.基于几何法的动力学收敛后的精度明显高于几何法定轨,而且可以实时得到卫星的速度。

6结束语

本文结合几何法和动力法的优点,从基本原理出发,在理论上给出了动力模型和观测模型,基于扩展卡尔曼滤波方法详细推导了基于几何法的动力学定轨方法。根据实际定位结果,基于几何法的动力学定轨方法与常规几何法定轨方法相比,卫星轨道三维位置误差更小,定轨误差波动也较小,结果相对稳定。因此,基于几何法的动力学定轨方法要优于常规的几何法定轨结果。

参考文献

[1] VETTER J R.Fifty years of orbit determination:Development of modern astrodynamics methods[J].Johns Hopkins APL Technical Digest,2007,27(3):176-189.

[2] COLOMBO O L. The dynamics of global positioning orbits and the determination of precise ephemerides[J].Journal of Geophysical,1989(94):9167-9182.

[3] 韩保民. 基于星载GPS双频观测值的简化动力学定轨方法[J]. 南京航空航天大学学报,2007,39(2):149-153.

[4] 韩保民. 动力学模型对简化动力学定轨精度影响仿真[J]. 系统仿真学报,2006,18(10):2722-2724.

[5] YUNCK T P. Orbital determination, global positioning system: Theory and applications[J]. American Institute of Aeronautics and Astronautics, 1996(2):559-592.

[6] 韩保民,欧吉坤,曲国庆. 一种新的综合Kalman滤波及其在星载GPS低轨卫星定轨中的应用[J]. 武汉大学学报·信息科学版,2005,30(6):493-496.

[7] 贾沛璋. 卡尔曼滤波定轨算法的研究进展[J]. 飞行器测控学报,2001,20(3):45-50.

[8] 余江林, 柳东升.卡尔曼滤波在利用GPS对GEO星定轨中的应用[J].全球定位系统,2000,26(3):26-29.

[9] KALMAN R E.A new application to linear and prediction theory[J].Journal of Basic Engineering, 1960:35-46.

[10]KAIMAN R E, BUCY R S.New results in linear filtering and prediction theory[J].Journal of Basic Engineering,1961:95-108.

周田(1988-),男,助理工程师,主要研究方向为卫星导航。

张辉(1985-),男,硕士,助理工程师,主要研究方向为卫星导航。

孙江艳(1986-),女,硕士,助理工程师,主要研究方向为卫星导航。

李博(1981-),男,工程师,主要研究方向为卫星导航。

Based on the Geometric Method and the Dynamics of the

Orbit Determination Method Research

ZHOU Tian,ZHANG Hui,SUN Jiangyan,LI Bo