面向方形节点拓扑地图下的移动机器人路径规划算法研究

，，

(哈尔滨工业大学机器人技术与系统国家重点实验室，哈尔滨 150001)

Research on Path Planning Algorithm for Mobile RobotBased on Square Nodes in Topological Map

LI Minglei，ZHAO Jie，LI Ge

(State Key Laboratory of Robotics and System，Harbin Institute of Technology，Harbin 150001，China)

面向方形节点拓扑地图下的移动机器人路径规划算法研究

李明磊，赵杰，李戈

(哈尔滨工业大学机器人技术与系统国家重点实验室，哈尔滨 150001)

ResearchonPathPlanningAlgorithmforMobileRobotBasedonSquareNodesinTopologicalMap

LIMinglei，ZHAOJie，LIGe

(StateKeyLaboratoryofRoboticsandSystem，HarbinInstituteofTechnology，Harbin150001，China)

摘要：针对方形节点拓扑地图下的移动机器人的特性，采用了A*算法来实现路径规划，并对传统的A*算法进行改进，一是在启发函数中引入了位移和角度2个因素，提高了函数的启发性；二是引入堆的方法优化了数据结构，提高了列表中代价最小节点的搜索速度。仿真实验结果表明，改进后的A*算法节点的最短路径节点相对减少，算法效率明显提高，具有良好的可行性和有效性。

关键词：移动机器人；拓扑地图；轨迹规划；A*算法

中图分类号：TP301.6

文献标识码：A

文章编号：1001-2257(2015)10-0067-04

收稿日期：2015-05-28

Abstract：In order to achieve the goal，according to the characteristics of the mobile robot based on square nodes in topological map，the paper improved the A* algorithm as follow. First，the new heuristic function took consideration of two factors：Distance and angle，improved the heuristic ability of A*；Then，the slowest part of the A* pathfinding algorithm is finding the node in the list with the lowest F score，the paper used the binary heaps to make it faster. Simulation results showed that the improved A* decreased the number of result nodes and took less time，demonstrated the feasibility and validity of the algorithm.

作者简介：李明磊(1990-)，男，山东潍坊人，硕士研究生，研究方向为机器人技术。

Keywords：mobilerobot；topologicalmap；pathplanning；A* algorithm

0引言

在移动机器人技术相关的研究中，路径规划算法是一个重要的领域，其核心是按照某一性能指标(如距离、时间等)，快速高效地在有障碍的工作环境中找到两个或者多个节点之间的最优或次优路径。现有的路径规划算法有很多，例如Dijkstra算法、遗传算法等。Dijkstra算法不考虑目标信息，需要遍历计算所有节点，虽然可以找到最短路径，但求解时间长，效率非常低。遗传算法也存在求解效率低，难以解决大计算量，容易陷入“早熟”等问题。

A*算法是一种典型的启发式搜索算法，一般适用于环境信息已知的全局路径规划中。该算法的核心在于引入了估价函数，从而避免了大量的无效搜索，提高了算法的效率。针对方形节点拓扑地图下移动机器人的特性，对A*算法进行了改进，在启发函数中引入了位移和角度2个参数，让规划轨迹更加合理；另外，还采用堆排序的方法优化了算法的数据结构，提高了算法的搜索效率。

1问题描述

方形节点拓扑地图下移动机器人的工作环境可以看作是二维平面上以正方形或者三角形方式阵列分布的圆形管孔，在环境中存在固定管、堵管等映射成不能通过的障碍区域。记移动机器人c在任意形状的二维平面区域a上运动，在区域U上随机的分布着不可达的有限数量的障碍物O{o1，o2，…，on}。为了便于规划，将任意形状的a区域补全为最小覆盖规整长方形区域，记为b，将补全的区域设置为障碍区域。

如图1所示，将区域b进行栅格化处理，将栅格地图映射到平面坐标系xOy上，定义原点O位于左上角，左上角的第1个栅格的坐标为(1，1)，记栅格地图的行列分别为m，n。记p为任意栅格，则栅格序号集{M，N}={(m1，n1)…(mi，nj)} 与P的坐标集{X，Y}={(x1，y1)…(xi，yj)}构成映射关系。

图1　栅格化的拓扑环境

栅格地图上的轨迹规划可以描述为在区域b上移动机器人c从既定起点s找到一条最优或者次优路径安全无碰撞的到达目标点t。

2基于传统A*算法的路径规划

2.1　算法的基本原理和符号定义

传统的A*算法的基本原理和Dijkstra算法相似，也是通过试探某个节点到目标节点的所有可能路径，最后找到最优解，但是由于A*算法引入了估价函数来估价每一步的代价，从而能更好的找到合适的搜索方向。A*算法是一种可采纳的最好优先算法，也就是说，如果待解决的问题存在最优解且引入的估价函数满足相容性条件，那么利用该算法就一定能够找到最优解。A*算法的估价函数可表示为：

(1)

g′(n)是起始点n到当前节点的路径代价；h′(n)是节点n到目标最低耗散路径的估计耗散值。节点之间距离的计算方式有很多种，采用了曼哈顿(Manhattan)距离为：

(2)

此外，还需要注意h′(n)启发函数的信息性。h′(n)的信息性通俗点说其实就是在估计一个节点的值时的约束条件，如果信息越多或约束条件越多则排除的节点就越多，启发函数越好或说这个算法越好。但在工程开发中由于实时性的问题，h′(n)的信息越多，它的计算量就越大，耗费的时间就越多，就必须适当的减小h′(n)的信息，即减小约束条件，从而导致算法的准确性就差了，这里就有一个平衡的问题。对A*算法具体符号定义如表1所示。

表1符号定义

符号意义p拓展过程中栅格地图上的节点n完成拓展的某一节点Ω节点p的八邻域节点构成的状态空间g(n)起点s到节点n的实际路径代价h(n)启发函数,n到目标节点t的估计代价f(n)估价函数,g(n)+h(n)Exp节点拓展函数Add节点插入函数Openlist待拓展节点集合Closelist已经拓展过的节点集合

2.2　算法流程图

基于A*算法，给出移动机器人轨迹规划流程如图2所示。通过计算可以得到规划路径Path。

图2　A*算法路径规划流程

3改进的A*算法

3.1　A*算法的估价函数

A*算法作为一种启发式搜索算法，其核心就在于设计一个合适的启发函数。图3为拓扑地图下移动机器人的二维示意图，机器人共包括基座、足部和脚趾。在其工作的过程中，基座和足部可以进行平动和转动，二者都需要耗费时间，因此在进行轨迹规划的过程中，不仅要考虑移动，还要考虑转动因素。

在启发函数的构造中引入了位移和角度2个要素，即

(3)

L为当前节点和目标点的曼哈顿距离；α是起点到当前节点的向量和当前点到目标点向量的夹角。w1，w2分别是位移和角度的加权值，其取值范围分别是0.55～0.65和0.35～0.45。具体加权值要根据地图类型和机器人参数进行调整。

(4)

n为可拓展节点数量。

通过归一化处理后，启发函数可以表示为：

(5)

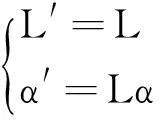
(6)

通过这种方式，可以解决位移容易产生压倒性作用的问题，二因素具体加权值还要根据具体工程要求进行调整。

3.2　利用二叉堆优化Openlist列表

A*算法中，最耗时的部分就是如何从Openlist中查找到估计函数值最小的节点，其影响程度随着节点数的增多越来越严重。在一般的A*算法中为了优化搜索时间，一般将节点排序存储，例如冒泡法，在搜索过程中需要遍历整个Openlist，其时间复杂度是O(n2)，整个搜索速度比较慢。

为了优化Openlist中最小F值的查找速度，采用二叉堆来优化数据结构。A*算法并不需要整个Openlist完全有序，只需要能够找到整个列表中F值最小的即可，这也为我们使用二叉堆提供了条件。

二叉堆法分为最小二叉堆和最大二叉堆2种。采用的是最小二叉堆，其父节点的值总是小于其子节点，整个数列中最小的值在堆稳定后总是在堆的最顶端。用一维数组来表示二叉堆时，编号为n(n>=1) 的节点，其子节点的编号为2n和2n+1，其父节点的编号为n/2，具体如图4所示。

图4　最小二叉堆数组

显然堆的第1个节点就是F值最小的点，从Openlist中取出堆顶节点后，为了使堆结构保持稳定，需要将最后一个节点移动到顶点，并和其子节点比较，如果父节点比子节点大，就交换二者位置，直到父节点比俩个子节点都小。当向堆中增加节点时，将新节点添加到堆的最后，然后与父节点比较，按照最小堆的特性进行比较，直到新节点大于其父节点或到达堆顶点。

使用最小二叉堆的方式从Openlist中找到F值最小的节点，算法的时间复杂度就可以近似地认为是O(logn)，从理论分析，可以有效地优化搜索效率。

4试验及分析

实验环境为：CPU Intel i5 3230，内存8 G，编译环境为Eclipse 3.2，对不同规模的障碍孔随机分布的栅格地图进行轨迹规划，并给出试验结果。

为了比较传统A*算法和改进后A*算法的效率，设计了2种类型的试验方案。

试验1。增大搜索空间，栅格地图采用16×16(如图5)，32×32……。具体试验结果如表2所示。

图5地图16×16

试验2。在相同的搜索空间下，改变障碍孔的复杂程度。采用改进后的A*算法，搜索空间为128×128，具体实验结果如表3所示。

表2不同规模栅格地图算法性能参数比较

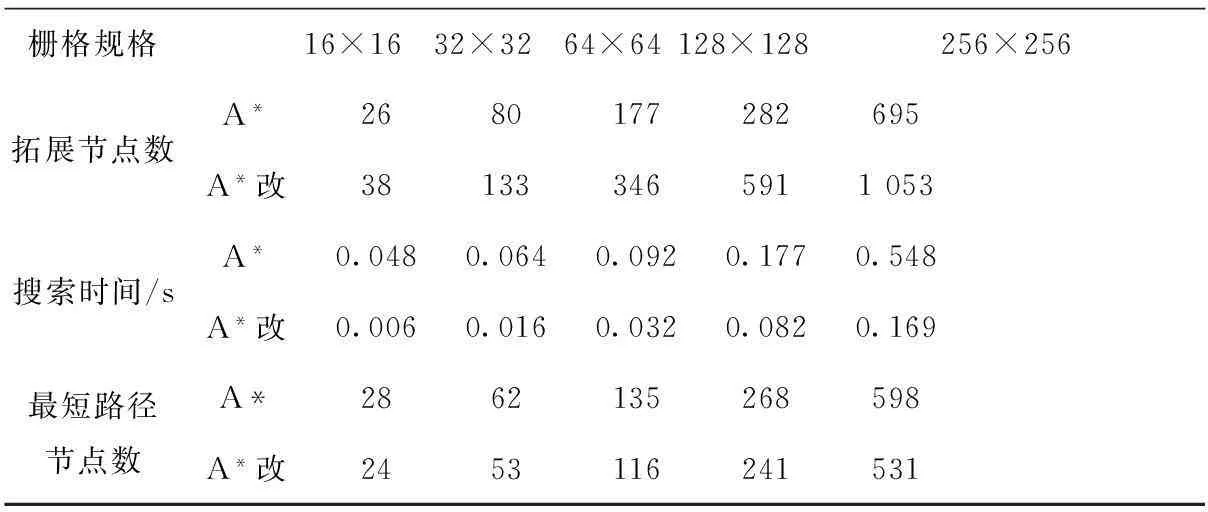
栅格规格16×1632×3264×64128×128256×256拓展节点数A*2680177282695A*改381333465911053搜索时间/sA*0.0480.0640.0920.1770.548A*改0.0060.0160.0320.0820.169最短路径节点数A*2862135268598A*改2453116241531

表3不同复杂度算法性能比较

障碍孔复杂度拓展节点数搜索时间/s最短路径节点数10%4190.08416320%4680.09618233%5190.10523150%6110.104310

①改进A*算法极大的提高了搜索的效率，如表2所示，改进后A*算法比传统A*算法搜索时间大大减少，并且随着搜索空间的增大，效果越来越明显，如图6所示；②改进A*算法由于改进了启发函数，可以通过更短的节点路径找到目标点；③改进A*算法在搜索过程中拓展的节点数明显增多，需要占用更多的系统空间，但在可接受范围内；④当障碍孔复杂度改变时，算法的拓展节点和最短路径节点数都有所增加，搜索时间的变化趋势不太明显并且在多次试验过程中都能找到解，说明在当前环境中，当障碍孔随机分布时对搜索效率影响不大。

图6　算法效率对比

5结束语

针对拓扑地图下移动机器人的轨迹规划，在传统A*算法的基础上，启发函数中引入了位移和角度2个因素，增加了函数的启发性，并对存储数据结构利用堆原理进行了改进，提高了算法的搜索效率。仿真试验结果证明了改进后算法的合理性和有效性，搜索效率和最短路径都得到了优化。

参考文献：

蔡自兴，谢斌.机器人学.北京：清华大学出版社，2015.

Anthony Stentz. A real-time resolution optimal re-planner for globally constrained problems// The 18th National Conf on Artificial Intelligence. Cambridge，MA：MIT Press，2002：1088-1096.

Latombe J C. Robot motion planning . Kluwer Academic Publishing，Norwell，MA，1991.

Begum M，Mann G K I，Gosine R G. Integrated fuzzy logic and genetic algorithmic approach for simultaneous localization and mapping of mobile robots . Applied Soft Computing，2008，8(1)：150-165.

Stuart Russell，Peter Norvig. Artificial Intelligence：A Modern Approach . Pearson，3 edition，2009.

Hans W Guesgen，Debasis Mitra. A multiple-platform decentralized route finding system .IEA/AIE99，LNAI 1611，2001，707-713.

Andre LaMotte. Windows游戏编程大师技巧.北京：人民邮电出版社，2004.

Taeg-Keun Whangbo.Efficient Bidirectional A*algorithm for optimal route-finding . IEA/AIE2007，LNAI 4570，344-353，2007.

Thomas H Cormen，Charles E Leiserson，Ronald L.算法导论 .北京：机械工业出版社，2013.