飞翼布局无人机二阶滑模姿态跟踪鲁棒控制

(1．西北工业大学无人机特种技术重点实验室，陕西西安　710072) 2．西北工业大学无人机研究所，陕西西安　710072



飞翼布局无人机二阶滑模姿态跟踪鲁棒控制

谭健1，周洲1，祝小平2，许晓平1

(1．西北工业大学无人机特种技术重点实验室，陕西西安710072) 2．西北工业大学无人机研究所，陕西西安710072

摘要:针对飞翼布局无人机受扰姿态控制问题，提出一种二阶滑模姿态跟踪鲁棒控制方案。基于时标分离特性，将飞翼布局无人机姿态控制系统分为内外回路进行设计。外回路采用自适应二阶终端滑模控制器，利用自适应算法调节切换增益抑制复合干扰对系统性能的影响，同时二阶终端滑模将不连续的符号函数加在控制量的导数上，通过积分得到连续的滑模控制律，从而有效地消除了常规滑模控制器的抖振。内回路采用基于自适应super twisting滑模观测器的积分滑模控制器，设计自适应super twisting滑模观测器以实现对内回路复合干扰的估计和补偿。最后通过控制分配环节将控制力矩分配到舵面上，仿真结果验证了所提方案的有效性。

关键词:飞翼布局无人机;二阶滑模;自适应;终端滑模; super twisting;观测器;控制分配

飞翼布局无人机出于气动效率及隐身特性的考虑，取消了平尾和垂尾等部件，具有纵向稳定性弱、航向中性稳定、横航向运动耦合强等一些问题，需要采用具有良好鲁棒性的非线性控制器以克服复合干扰的影响。滑模变结构控制具有设计简单、鲁棒性强以及在滑模运动阶段对干扰具有不变性等优点，近年来在航空器的控制系统设计中有诸多应用［1-2］。与自适应控制技术相结合，确定变结构控制切换增益无须知道无人机复合干扰的上界，自适应滑模变结构的切换增益值采用自适应算法获得。尽管采用自适应算法，切换增益值有所减小，然而，不连续符号函数依然会引起系统的抖振，抖振现象的存在限制了自适应滑模变结构控制的应用。采用准滑动模态的控制方法，将控制律不连续的符号函数替换为连续的饱和函数的方法可以有效抑制抖振，但是在抑制抖振的同时，会牺牲系统的鲁棒性［3］。近年来高阶滑模［4-5］得到了许多学者的重视，不连续符号函数施加在控制律的一阶或高阶导数上，在积分的作用下，得到连续的滑模控制律，有效地削弱了控制器的抖振。

为保证飞行控制的性能，采用干扰观测器估计与补偿干扰，也是抑制复合干扰影响的良好方法。文献［6］对super twisting算法进行了改进，提出了自适应super twisting二阶滑模控制算法，对于未知有界的连续干扰，可保证受扰系统的状态有限时间内收敛到滑模流形s==0上，基于此二阶滑模算法设计的自适应super twisting二阶滑模干扰观测器，将符号函数隐藏在积分项里，得到连续的干扰补偿值，避免了抖振造成控制系统的不稳定。

基于以上分析，本文提出一种二阶滑模姿态跟踪鲁棒控制方案，外回路采用自适应二阶终端滑模控制器，利用自适应算法调节切换增益抑制复合干扰对系统性能的影响，通过二阶终端滑模将符号函数隐藏在积分项中得到连续的控制输入。内回路采用基于自适应super twisting二阶滑模干扰观测器的积分滑模控制器，利用二阶滑模观测器得到连续的干扰补偿值抑制内回路复合干扰的影响。考虑到飞翼布局无人机的多舵面布局和存在舵效非线性、舵面附加力的问题，采用非线性控制分配，按照阻力最小的优化目标将控制力矩分配到舵面上。最后，仿真结果验证了所提出的方法具有良好的控制性能。

1　飞翼布局无人机姿态模型

飞翼布局无人机的舵面配置如图1所示，为4 组8个舵面。从内到外分别布置了升降舵舵1、升降副翼舵2和舵3以及开裂式方向舵舵4。

图1　飞翼布局无人机舵面配置

考虑到未建模动态与外界扰动，无人机的姿态模型为包含不确定项的非线性方程组:

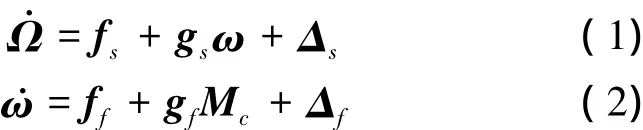
式中，Ω=［α β μ］T分别为无人机的迎角、侧滑角和滚转角，ω=［p q r］T分别为滚转角速率、俯仰角速率和偏航角速率，fs，ff为姿态模型精确建模部分，gs为与状态变量相关的矩阵，gf为与惯量矩相关的矩阵，具体表达式参见文献［7］。Mc为舵面产生的滚转、俯仰和偏航控制力矩，与舵面偏角的关系式为

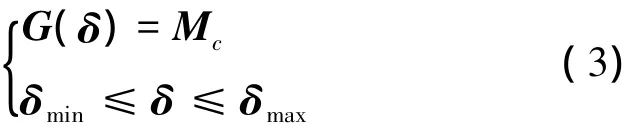
式中，δ，δmin，δmax都为8×1维向量，δ为无人机8个舵面的舵面偏角，δmin，δmax分别为舵面偏角位置约束的最小和最大值，G(δ)是与舵面偏角δ有关的非线性函数。Δs，Δf是未建模动态与外界干扰等产生的姿态模型复合干扰，有如下表达式

式中，Δfs，Δff，Δgs，Δgf为系统的未建模动态，ds，df为外界干扰。基于时间尺度将无人机姿态控制系统分为外回路和内回路分别设计，其中外回路为姿态角回路(1)，内回路为姿态角速率回路(2)。

2　外回路自适应二阶终端滑模控制器

飞翼布局无人机姿态模型的外回路为一阶系统，由高阶滑模的特性可知，对外回路采用二阶滑模控制，将符号函数隐藏在积分项中得到连续的控制输入，可以有效的抑制控制律的抖振。同时，为了提高外回路控制精度，设计了如下的积分滑模面:

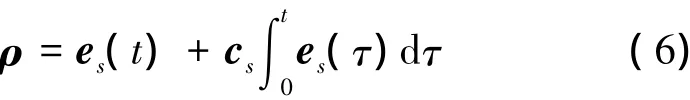
式中，Ωc为姿态跟踪目标指令，es=Ω－Ωc，cs= diag(cs，1，cs，2，cs，3)为积分参数且各分量大于零，ρ= ［ρ1ρ2ρ3］T。

设计如下的非奇异终端滑模用以实现姿态控制系统外回路的二阶滑模控制:

式中，参数η= diag(η1，η2，η3)且各分量大于零，=［］T，p，q为奇数，且满足1＜p/q＜2，滑模面Ss=［Ss，1Ss，2Ss，3］T。

定理1对于无人机姿态控制系统外回路

如果复合干扰Δs=［Δs，1Δs，2Δs，3］T连续可微且一阶导数有界，即||＜θi(i = 1，2，3)。采用控制律(8)式与自适应律(9)式所示的自适应二阶终端滑模控制器时，外回路闭环是渐近稳定的。

式中，λ= diag(λ1，λ2，λ3)，ξ= diag(ξ1，ξ2，ξ3)且各分量大于0，

证明:取Lyapunov函数为

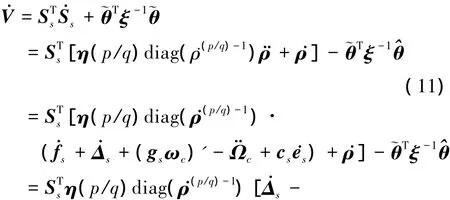
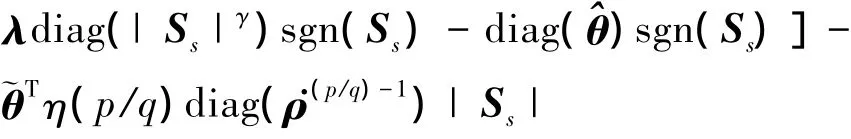
当滑模面Ss≠0，由文献［8］可知，若= 0，ρi≠0，则系统处于不稳定状态。p，q为奇数且满足1＜p/q＜2，当≠0时，则存在＞0。外回路复合干扰连续可微且一阶导数有界，即有||＜θi(i = 1，2，3)，由(11)式可得

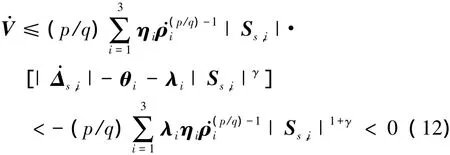
设在tr时间内系统收敛到滑模面Ss= 0，由终端滑模的性质可知，ρi将在tr时间后的有限时间内收敛到零，当ρi= 0，由积分滑模的性质可知，外回路稳态误差es=Ω－Ωc将渐近收敛到零，外回路闭环是渐近稳定的，定理1得证。

3　内回路二阶滑模控制器设计

3. 1自适应super twisting二阶滑模干扰观测器

考虑到飞翼布局无人机的内回路存在复合干扰，设计如下的自适应super twisting二阶滑模干扰观测器对复合干扰进行估计与补偿。

定理2对于无人机姿态控制系统内回路，若复合干扰Δf=［Δf，1，Δf，2，Δf，3］T连续且有界，设计如下自适应super twisting二阶滑模干扰观测器:

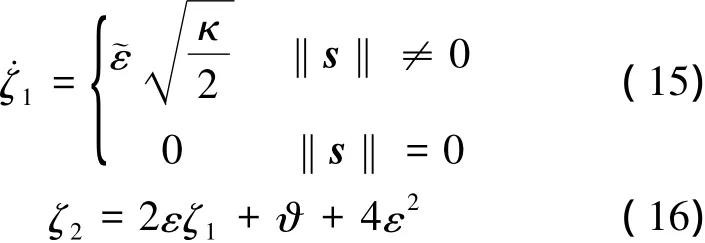
为证明定理2，首先给出引理:

引理1若干扰Δ连续可微且有界，对于受扰自适应super twisting二阶滑模控制算法［6］

若参数φ1，φ2采用如下自适应律，则系统状态有限时间收敛到σ(t) =(t) = 0。

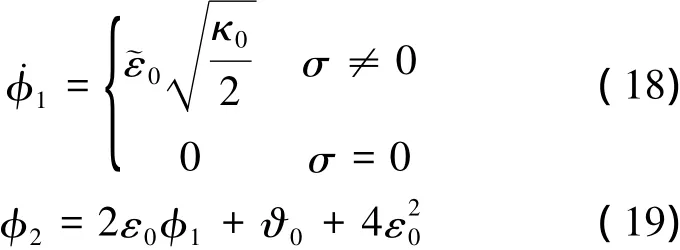
证明:式(1)减去式(13)得

可知，在有限时间内，内回路复合干扰Δf可由(14)式的估计，由(14)式可以看出，自适应super twisting二阶滑模观测器将不连续符号函数sign隐藏积分项里，抑制了常规滑模观测器的抖振现象。

3. 2滑模干扰观测器补偿复合干扰

积分滑模面可有效提高控制器的精度与鲁棒性，为内回路设计如下的积分滑模面:

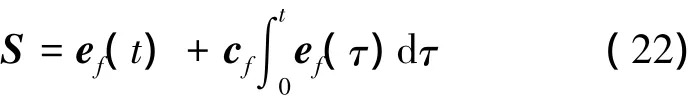
式中，ef=ω－ωc，cf= diag(cf，1，cf，2，cf，3)为积分项参数且各分量大于0，S =［S1，S2，S3］T。

定理3对于无人机姿态控制系统内回路，若复合干扰Δf=［Δf，1，Δf，2，Δf，3］T连续且有界，采用如(23)式所示基于自适应super twisting二阶滑模观测器的积分滑模控制器时，内回路闭环是渐近稳定的。

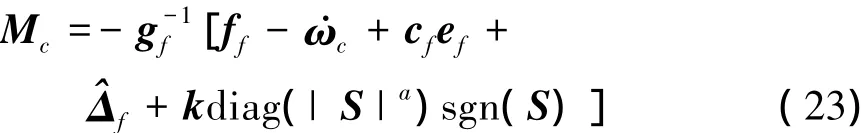
式中，sgn(S) =［sgn(S1)sgn(S2)sgn(S3)］T，滑模控制器参数k = diag(k1，k2，k3)且各分量大于0，diag(| S|a) =diag(| S1|a，| S2|a，| S3|a)，指数a∈(0，1)。

证明:选取Lyapunov函数为

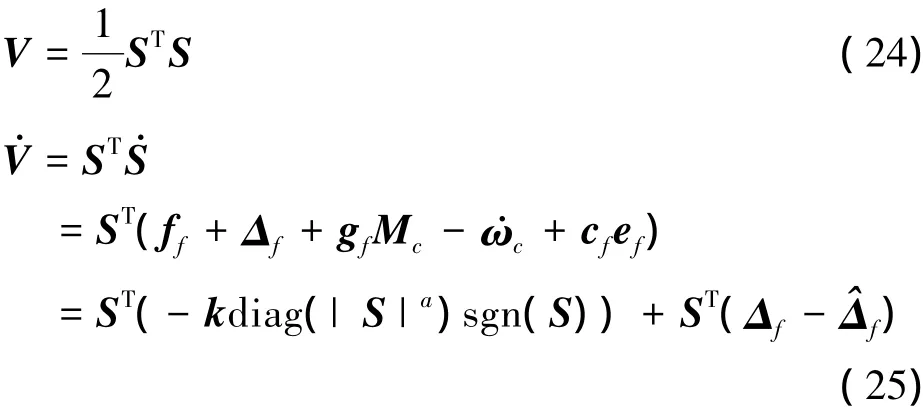
自适应super twisting二阶滑模干扰观测器可在有限时间内实现Δf－^Δf= 0。滑模控制律已经实现了内回路各通道间的解耦，对于内回路单个通道有

在有限时间内系统轨迹会到达每一个通道的滑模面Si= 0(i = 1，2，3)，即S = 0，此后开始进行滑模运动，积分滑模面可保证内回路稳态误差渐近收敛到零，定理3得证。

内回路控制律设计得到的是三轴方向上的舵面控制力矩。为充分利用冗余舵面与解决非线性舵效、舵面附加阻力等问题，采用非线性控制分配求解舵面偏角，控制分配以姿态控制时舵面附加阻力最小为优化目标。

式中，J为优化目标，CDδ为控制分配舵面附加的阻力系数，非线性控制分配采用非线性规划方法进行求解。

4　数值仿真

4. 1仿真参数设定

飞翼布局无人机的初始状态为V = 0. 6Ma，α0= 1. 8°，β0= 0°，μ0= 0°，p0= q0= r0= 0 rad/s。

外回路和内回路复合干扰分别为

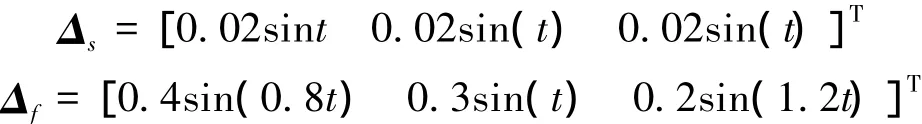
姿态跟踪目标指令为

αc= 5°，βc= 4°，μc= 3°

控制器参数为

p = 7q = 5η= diag(1，1，1)γ= 0. 5

cs= diag(0. 01，0. 01，0. 01)

λ= diag(0. 5，0. 5，0. 5)

ξ= diag(2，2，2)

cf= diag(0. 01，0. 01，0. 01)

k = diag(2，2，2)，a = 0. 5

自适应super twisting二阶滑模观测器参数

ζ1(0) = 0，珘ε= 1，κ= 1，ε= 0. 5，= 1

为了说明本文所提方法的有效性，现对以下2种控制方案进行比较。

控制方案1:外回路采用自适应二阶终端滑模控制器，内回路采用基于super twisting二阶滑模干扰观测器的积分滑模控制器。

控制方案2:去除控制方案1外回路的自适应律和内回路的自适应super twisting二阶滑模干扰观测器，其他与控制方案1相同。

4. 2仿真结果对比与分析

图2～图4为2种控制方案下飞翼布局无人机迎角、侧滑角和速度滚转角响应曲线，在系统具有复合干扰的情况下，控制方案1很好跟踪了控制指令，控制无超调，收敛速度快，稳态精度高，有效抑制了复合干扰的影响，鲁棒性好。控制方案2没有跟踪上控制指令，迎角、侧滑角和速度滚转角都围绕着控制指令振荡，动态特性很差。

图2　迎角响应曲线

图3　侧滑角响应曲线

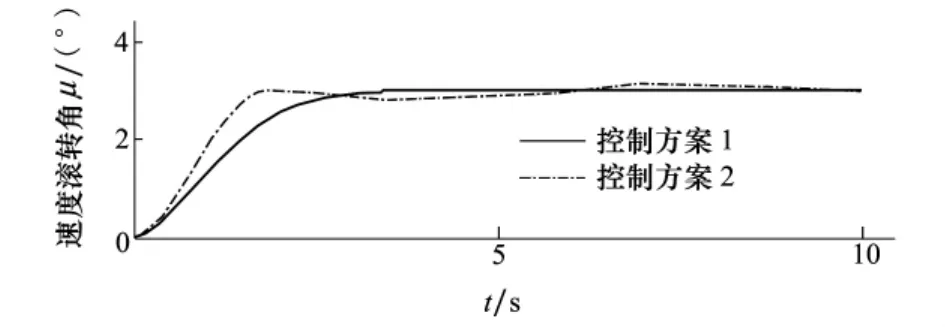
图4　速度滚转角响应曲线

滑模干扰观测器用来实现对复合干扰的估计与补偿，控制方案1对内回路各通道复合干扰的估计如图5所示，观测器的干扰估计曲线与复合干扰曲线基本重合，很快实现了对复合干扰的估计，因此从姿态控制的鲁棒性、跟踪精确、收敛速度，控制方案1都具有较好的效果。

控制方案1的舵面偏角如图6所示。由于本文控制方案1外回路采用自适应二阶终端滑模控制器，通过二阶终端滑模将符号函数隐藏在积分项中得到连续的控制输入。内回路采用自适应super twisting二阶滑模干扰观测器得到连续的干扰补偿值，同时采用具有二阶滑模特性的幂次趋近律，抑制了姿态控制系统的抖振，因此，舵面偏角曲线平滑无抖振。从图7可以看出，右开裂式阻力方向舵δr4和左开裂式阻力方向舵δl4始终单侧偏转，与非线性控制分配的优化目标附加阻力最小一致。

图5　内回路各通道干扰与干扰估计

图6　控制方案1舵面偏角

5　结论

针对飞翼布局无人机受扰姿态控制问题，提出了二阶滑模姿态跟踪鲁棒控制方案，分别利用自适应控制与自适应super twisting二阶滑模干扰观测器抑制外回路、内回路复合干扰的影响，由于二阶滑模的采用，有效的减小了常规滑模控制器的抖振现象，本文所提方法更适于工程实践应用，仿真结果也验证了其有效性。

参考文献:

［1］Besnard L，Shtessel Y B，Landrum B．Quadrotor Vehicle Control Via Sliding Mode Controller Driven by Sliding Mode Disturbance Observer［J］．Journal of the Franklin Institute，2012，349(2) : 658-684

［2］Khatri A K，Singh J，Sinha N K．Aircraft Maneuver Design Using Bifurcation Analysis and Sliding Mode Control Techniques ［J］．Journal of Guidance，Control，and Dynamics，2012，35(5) : 1435-1449

［3］曾宪法，王洁瑶，王小虎，等．基于SMDO的滑模控制器设计及其在导弹上的应［J］．航空学报，2011，32(5) : 873-880 Zeng Xianfa，Wang Jieyao，Wang Xiaohu，et al．Design of Sliding Mode Controller Based on SMDO and Its Application to Missile Control［J］．Acta Aeronautica et Astronautica Sinica，2011，32(5) : 873-880 (in Chinese)

［4］Levant A．Homogeneity Approach to High-Order Sliding Mode Design［J］．Automatica，2005，41(5) : 823-830

［5］Shtessel Y B，Shkolnikov I A，Levant A．Smooth Second-Order Sliding Modes: Missile Guidance Application［J］．Automatica，2007，43(8) : 1470-1476

［6］Yuri B S，Jaime A M，Franck Plestan，et al．Super-Twisting Adaptive Sliding Mode Control: a Lyapunov Design［C］∥49th IEEE Conference on Decision and Control，Atlanta，GA，USA，2010: 15-17

［7］张强，吴庆宪，姜长生，等．考虑执行器动态和输入受限的近空间飞行器鲁棒可重构跟踪控制［J］．控制理论与应用，2012，29(10) : 1263-1271 Zhang Qiang，Wu Qingxian，Jiang Changsheng，et al．Robust Reconfigurable Tracking Control of Near Space Vehicle with Actuator Dynamic and Input Constraints［J］．Control Theory＆Application，2012，29(10) : 1263-1271 (in Chinese)

［8］Feng Y，Yu X Y，Man Z H．Non-Singular Adaptive Termi-nal Sliding Mode Control of Rigid Manipulators．Automatica，2002，38(12) : 2159-2167

Second Order Sliding Mode Attitude Tracking and Robust Control of Flying-Wing UAV

Tan Jian1，Zhou Zhou1，Zhu Xiaoping2，Xu Xiaoping1

(1．State Key Laboratory of UAV Special Technology at Northwestern Polytechnical University，Xi'an 710072 China 2．Research institute of unmanned Aerial Vehicle，Northwestern polytechnical University，Xi'an 710072，China)

Abstract:We propose a second order sliding mode attitude tracking and robust control strategy for the flying-wing unmanned aerial vehicle(UAV) with unknown external interferences．We take into account its timescale separation property and design its attitude control system into outer loop and inner loop．The outer loop uses the adaptive second order sliding mode controller and the adaptive algorithm to adjust the switch gains and suppress the influence of compound interference on the performance of the flying－wing UAV．The second order sliding mode controller adds the discontinuous sign function to the derivative of the control volume and obtains through integration the continuous sliding mode law，thus effectively eliminating the chattering of the conventional sliding mode controller．The inner loop uses the integral sliding mode controller based on the adaptive super twisting sliding mode observer．The adaptive super twisting sliding mode observer is for estimating and compensating for the compound interference of the inner loop．Finally，we use control allocation to allocate control moment to the rudder surface of the control system．The simulation results show preliminarily that our strategy is effective．

Key words:adaptive algorithms，angle of attack，angular velocity，attitude control，computer software，computer simulation，control，controllers，convergence of numerical methods，design，drag coefficient，flight control systems，Lyapunov functions，matrix algebra，robust control，sliding mode control，unmanned aerial vehicles(UAV) ; flying-wing UAV，second order sliding mode，super twisting，observer，power approximation，control allocation

作者简介:谭健(1989—)，西北工业大学博士研究生，主要从事无人机飞行控制研究。

收稿日期:2014-09-28基金项目:国家自然科学基金(11302178)资助

文章编号:1000-2758(2015) 02-0185-06

文献标志码:A

中图分类号:TP273