基于高斯阈值法的水电机组状态评估方法研究

许红义

（北京十三陵蓄能电厂，北京市 102200）

1 概述

常规的水电机组故障诊断与推理系统需要足够的故障知识来支撑，而水电机组系统复杂、电站参数各异、机组型式也各不相同，有些故障机理目前也尚不清楚。因此现阶段要建立全面的水电机组故障诊断知识库非常困难。而故障样本的缺失，导致基于知识的水电机组故障诊断和专家系统很难在实际应用中起到应有的作用，也严重制约了诊断理论方法在水电工程中的应用与发展。

针对现阶段水电机组故障样本少，但电站已经安装了大量机组状态监测设备的实际情况，如何利用其长期的监测数据，预测和避免故障的发生，并指导机组检修，是水电行业状态监测与故障诊断技术研究与应用面临的一个重大挑战。而基于统计学的新异类检测（Novelty Detection）方法，可以充分利用机组监测数据，通过检验新的数据对已知样本的偏离程度，来判断机组是否发生了异常，从而使得小故障样本的水电机组故障诊断与寿命预估成为可能。

水电机组“故障”表现可能多种多样，但其“正常”状态却是有限的，健康样本也易于采集收集和健全。这一诊断理念侧重于设备运行状态的实时健康诊断，重点在于监测异常和预测异常，而不是过多的去查找和分析发生故障的原因，与现有的故障诊断方法有很大的差异。根据机组状态监测信息，判定机组运行状态是否正常，一旦出现异常，可启动系统智能诊断，对于系统无法诊断的故障，可采用人工辅助诊断、专家协同会诊，甚至停机检查、拆卸检查、专项试验等手段来完成故障分析。鉴于水电机组实际运行中，出现的故障概率较小，基于该诊断理念开发的诊断系统工程实用性很强，且系统具备实时健康诊断和量化的性能退化趋势预测功能，既能实时监测异常，又能预测异常，可满足现阶段的工程应用需求。

因此，本文通过新异类检测方法中的健康样本模型与机组状态监测系统的结合，提出一套健全的基于水电机组健康模型的监测诊断方法来实现机组的健康诊断。该诊断方法侧重于设备运行状态的实时评估，而不过多的关注故障原因和机理等因素，通过监测设备状态是否存在异常及其严重程度，再结合故障推理或其他辅助手段来完成故障分析。

2 高斯阈值法

高斯阈值法属于密度估计方法的一种，其基本原理是估计出样本集的概率分布函数P(x)，并设定一个密度阈值，当测试样本的所在区域的密度高于该阈值时，判定其为正常，否则判定为异常。设x为水轮机状态监测系统的某振动信号（上机架Y向振动）的统计特征，显然他是随机变量，故样本x的特征值x服从高斯分布，x的均值为μ，标准差为δ，根据切比雪夫不等式，对于任意实数e＞0，有式（1）成立：

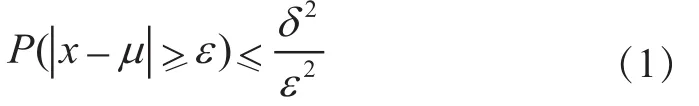
定义其带宽系数k＞0，并令e=kδ，则式（1）可以表示为：

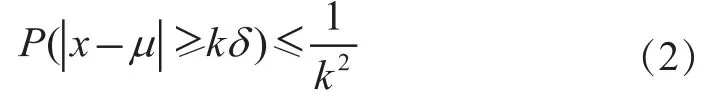
图1 高斯分布对应不同的标准差的范围

对状态监测系统而言，其状态数据一直处于实时更新中，而根据系统相关性，近期的状态数据更能反映机组真实的健康状态，因此，为了保证健康样本的有效性和自学习能力，这里采用滑动计算的自适应高斯阈值法。

对于特征序列xi，训练样本集将在xi中滑动，假设训练样本集时间长度定为T，在t-1时刻，训练样本集xi为当前的xi-1到前推T时间长度的样本xt-T，即训练样本集为：{xi,i=t-T,…,t-1}。这时高斯分布的均值μ、标准差δ和高斯密度阈值C分别为[1]：

而在t时刻，原训练样本中的xt-T删除，同时加入当前时刻t的样本xt，更新样本集为{xi,i=t-T+1,…,t}，其高斯分布的均值μ、标准差δ和高斯密度阈值C分别为：

3 状态评估方法研究

在水电站安装实施的水电机组状态监测系统中，实时保存了机组运行的大量监测数据，而在机组安装初期，或过去一段机组运行状态正常的区间内（可以在机组检修或历史数据分析中得到验证），可以认为这些历史数据，能够表征机组的健康状态，换言之，可以认为这些数据是机组健康运行时的状态信息。那么通过设定不同的阈值和统计限值，则可以对机组发生状态突变或超出预设限值时进行预警，起到异常检测的效果。

在水电机组运行状态中，有功功率和工作水头是非常重要的两个工况信息，因此本文将综合机组工况参数的变化（这里的有功功率也可换成转速、导叶开度等工况参数），建立机组运行状态的全工况网格，每一网格中对应该特定工况下采集的某测量信号的大量历史数据，采用高斯阈值法得到其高斯密度阈值，作为特征参数，从而建立水电机组健康状态样本模型。而自适应高斯阈值法的引入，则使得该健康样本模型具有自学习能力，能够随着时间的发展而不偏离真实的健康样本特征。其具体步骤如下：

（1）确定机组运行健康状态，选取健康运行区间的数据。制定选取机组运行状态历史数据的依据，选取机组无信号报警和数据超限的运行时间段，提取某信号的历史特征值，以及对应的水头、工况值，作为机组健康状态的特征序列。

这里采用某大型混流式水电机组（额度功率70万kW）正常运行一年的实际监测数据（按每10分钟取均值，每测点约5.2万特征值），选用在稳态工况下其上机架X向垂直振动峰峰值，建立健康样本模型，并验证机组的异常检测有效性。图2为机组振动、有功数据趋势图。

（2）划分机组工况网格。根据有功功率的范围，结合数据采集和落在相应工况点的密度，确定样本模型的最小工况网格。如果最小工况网格划分过密，机组在部分过渡过程工况下运行时间较短，则有可能该工况网格内测点的样本值较少，无法计算有效的高斯密度阈值；如果最小工况网格划分过大，则无法准确反映机组该某工况下的运行健康特征。图3为机组360天有功值分布直方图。

（3）计算每个网格内的测量信号特征值的高斯密度，建立机组健康样本模型。对落在网格内部的大量特征序列值，进行高斯密度阈值计算，得到阈值范围通过对大量网格的统计计算，得到机组健康样本模型Ct［包括上下阈值

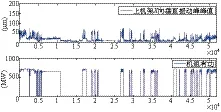
图2 机组振动、有功数据趋势图（360天5万数据点）

图3 360天有功值分布直方图

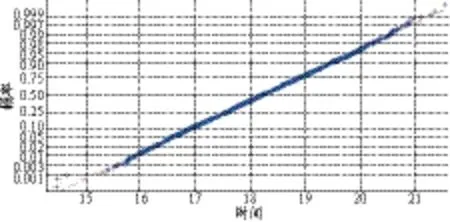
图4 概率分布检验图

通过选取稳态工况网格内[696.89，702.21]MW的数据，进行直方图检验，并通过matlab jbtest函数得到分布概率检验图，且得到测点均值18.2um，上下阈值采用3δ即99.87%置信度区间值为[15.4，21.0]。图4为概率分布检验图。

（4）引入自适应高斯阈值法，使样本模型具备自学习能力。在同一工况网格中，如果有新的实时监测数据出现，则采用滑动训练该网格内样本集的方法，实现样本模型Ct随数据的更新，从而更接近机组真实的运行状态。

4 结论

本文对某电站机组进行了长期的监测数据统计分析，确认了其振动特征值存在的正态分布规律，并利用自适应高斯阈值法进行滑动更新，能够实现报警限值之外的异常判断与分析。由于采用了99.87%的置信度区间报警阈值，可以保证绝对大部分情况下的异常识别和报警。另外，由于采用了网格划分，能够以网格形式进行报警统计阈值划分，能够为机组状态监测和故障诊断提供数据依据和有效的保障。

[1] 胡雷. 面向飞行器健康管理的新异类检测方法研究[D].国防科技大学.2010:56-57.

[2] 刘晓亭，冯辅周.水电机组运行设备监测诊断技术及应用[M].北京:中国水利水电出版社.2010.

[3] 陆春月，王俊元.机械故障诊断的现状与发展趋势[J].机械管理开发，2004.12（6）.

[4] 马宏忠. 电机状态监测与故障诊断[M].北京:机械工业出版社.2008.