基于 ObjectARX的复杂图形拆分及其实现

陈旭东++刘伯颖

在数控机床的操作过程中，编程工作是枯燥而乏味的，指令测试往往伴随着工件的浪费。以 Visual C++为开发工具，使用 ObjectARX开发接口，可直接读出 AutoCAD数据库中的设计图形数据。由设计图形数据出发，实现数控机床指令的自动编码与仿真，将大大提高工作的效率和准确性。本文提出的算法用可以将复杂的图形数据拆分为简单图形序列，从而提高自动编码系统的准确性，使系统自动编制出的数控机床机器指令达到最优。

一、引言

冲裁成型技术是工业中应用广泛的板材加工技术，一般是使用数控机床进行加工，数控机床使用特定的语句指令进行编程。这种编程一般使用数控系统高级语言FAGOR，通常称为G代码，如：G00 G90 X400 Y300，表示快速定位，G90表示绝对坐标。数控机床工作的过程就是执行 G代码的过程。使用 G代码不仅要控制加工位置，还要控制模具的切换，代码量较大。例如冲压 100个间隔相等的孔，通常需要编制至少200条指令。编写G代码的过程往往是繁琐枯燥的，正确性难以保证，进行指令的测试往往伴随着原材料的浪费。使用计算机辅助设计系统可以实现数控机床所需 G代码的自动化编程。

AutoCAD是美国 Autodesk公司推出的计算机辅助设计软件，广泛用于二维绘图、设计文档和基本的三维设计。其开放的体系结构，允许用户进行二次开发，根据自己的需要扩充新的功能。ObjectARX（Object AutoCAD Runtime eXtension）是 AutoCAD系统配套的面向对象的 C++应用程序开发接口，使用 ObjectARX可以在运行状态下直接访问 AutoCAD的内部数据库，图形系统及几何造型核心。使用 VC++开发基于 ObjectARX的应用，还可充分利用Windows系统资源，包括MFC基本类库和Visual C++开发环境。可以在运行时从 AutoCAD中读取设计图形数据。通过分析这些图形数据，可以实现冲床指令的自动编程与仿真，从而可以大大提高工作效率，降低甚至杜绝板材的测试浪费，提高经济效益。

二、问题的提出

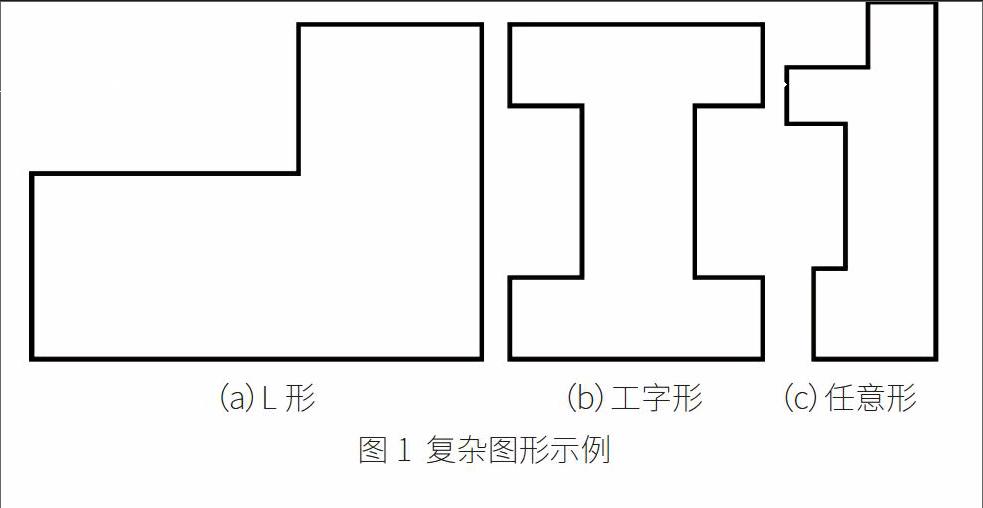
数控机床对于简单的图形，如三角形、矩形、圆形及长圆孔等（以下称为基本图形），都有成熟的加工指令或指令序列。而工业中需要加工的形状要复杂得多，包括凸多边形，凹多边形，甚至可能包括曲线边在内（以下称之为复杂图形），如图 1所示为典型的复杂图形示意图。这些图形在机床上无法简单的加工出来，需要编写机床控制程序。如果能将这些图形做一定的拆分，将其分解为多个矩形，就可以使用矩形的加工指令组成复杂多边形的加工指令。

通过 ObjectARX接口，可以读出 AutoCAD中的设计图形数据，并进行分析处理。本文提出的拆分算法的目的就是将各种各样的复杂形状拆分为较简单的基本图形，即把复杂图形看成是由基本图形拼成的，为复杂图形找到一组合理的基本图形序列，从而可以使用基本图形的加工指令进行复杂图形的加工。

三、复杂图形拆分算法描述

图形拆分算法的程序流程如图2所示。简要叙述如下。

（1）读取 AutoCAD中的设计图形数据，数据的顺序和设计图绘制过程有关，在数据排序链接模块中，需要对读出的数据进行预处理，按顺序依次排列组成封闭图形。因为工件上一般需要加工多处孔，所以此处得到的是一个封闭图形的序列。

（2）对序列中的图形依次进行处理，每次取出一个封闭图形。检测图形数据的转向，确保封闭图形数据按逆时针转向排列。否则对图形数据进行翻转处理。

（3）在图形数据逆时针转向的基础上，可以确定各顶点的内角。对凹多边形来讲，内角值有可能会大于 180°，确定图形内角对图形拆分模块有重要意义。

（4）图形拆分模块。这一部分将综合使用图形数据的各种信息进行图形的拆分，拆分的结果是形成一个基本图形的序列。

（5）最后输出拆分后的基本几何图形序列。

四、算法的实现

下面以L形图形的拆分为例，介绍复杂图形拆分的执行过程。本文的介绍是针对由直线段组成的多边形，在实际的应用中，可以根据具体的需要对算法进行扩展。

1.图形边框的数据定义

通过 ObjectARX接口，从 AutoCAD中读出数据后，将边框用以下数据结构来表示： b（x1，y1，x2，y2，angle）

式中， x1，y1表示边 b的起点坐标； x2，y2表示边 b的终点坐标；angle表示其与下一条边的内夹角。

设 L形的坐标数据如图 3所示。

以图 1中L形的分析为例，假设坐标如图 3所示，边框依次定义为 b1、b2、b3、b4、b5和 b6，数据自 AutoCAD中读出后，按点坐标检测数据是否组成封闭图形。经过处理后，边框数据表示如下：

2.封闭图形转向检测

由于在进行图形数据封闭连接的运算中，无法确定图形数据的顺序是按逆时针排序，还是顺时针排序。进行数据转向检测可以使用向量法，选取任一顶点，计算其指向其他各顶点的向量，如图 4所示。

计算各向量的向量角——即各向量与x轴的夹角。角度取值范围为 0～360°。向量角计算如下： v1：（370-120）+i（100-100）=250 向量角：arctan（0/250）=0° v2：（370-120）+i（300-100）=250+i200 向量角：arctan（200/250）]=38.70° v3：（270-120）+i（300-100）=150+i200 向量角：arctan（200/150）=53.1° v4：（270-120）+i（200-100）=150+i100 向量角：arctan（100/150）=33.69° v5：（120-120）+i（200-100）=i100 向量角：90°

由此可见，向量角从 0°增大到 90°，则可以确定封闭图形的旋转方向为逆时针方向，符合数据处理的要求。如果向量角检测的结果为减小，则说明数据的顺序为顺时针方向，需要对图形边框数据进行反向处理。

3.计算顶点对应的内角值

在封闭图形数据转向确定的情况下，无论是凸多边形，还是凹多边形，都很容易确定图形每个顶点所对应的内角大小。如图5所示。

4.图形拆分处理

将复杂图形拆分为基本图形是本算法的核心内容，前面的处理都是为这一步做准备。首先应该确定拆分的最终结果有几种基本图形。然后才能确定图形分割的具体过程如何。在此假设图形分割的最终目的是得到一个三角形和矩形的序列。该过程是一个循环，步骤简述如下。

（1）首先检测剩余边数，如果等于0，表示已没有剩余边框数据需要处理，转（8）；如果剩余边数小于 3且不等于0，则输出错误信息。

（2）如果等于三，则得到一个三角形。将三角形加入到基本图形列表，转（8）。

（3）查找内角值最大的边，取其下一条边作为起始边。检测其与末端顶点的内角，如果大于 180°，则继续选取下一条边。

（4）检测当前边与下一条边的夹角，如果为 90°，则继续读取下一条边。

（5）查看已读取到的边数，如果已读取到4条边，则转6，否则转（4）继续读取。

（6）检测读取到的四条边是否组成封闭矩形。如果是则将矩形合并到数据序列，转（1）开始下一次循环，否则转（7）进行图形运算。

（7）已读取的四条边，因为自第一条边起，到第四条边都是 90度，而图形现在没有封闭。必然是第一条边的起点和第四边的终点没有重合。可以将第一条边和第四条边转化为直线方程，求其交点。求出的矩形输出到基本图形列表。然后转（1）继续执行。

（8）得到基本图形序列后，按一定的规则进行优化，对于不符合最终要求的基本图形进行优化运算。

（9）最后输出优化后的所有矩形。

仍以 L形为例。首先查找到内夹角最大的点为p5，对应内角值为 270°；然后逆时针读取到b5、b6、b1和 b2共 4条边；进行图形封闭检测，可发现起点和终点不重合。以第一条边 b5和第四条边 b2为直线接方程，可求得交点p7，其坐标为（250，100）。

以点 p7为分割点，将原有线段 p2-p3分割为两个线段，将线段 p2-p7插入到输出矩形中，p7-p3插入到原始数据；线段p5-p7插入到原始数据组成新的封闭图形；插入p7-p5到输出矩形数据，由于 p7-p5和 p5-p6直线方程完全相同，可以合并为线段 p7-p6。继续循环，可得 p1-p7-p3-p4为一个矩形，输出到基本图形列表。 然后可按照一定的规则进行优化，使最终的分割结果近似最优，程序成功退出。至此一个图形拆分完成，如图 6所示。

同理，对图 1中的（b）的工字型执行该算法，可得拆分结果如图 7所示。对图1中的（c）执行该算法，可得拆分结果如图8所示。对于该任意形的拆分，由于拆分后所得矩形 4的宽度太小，不符合加工的最小宽度要求。可以将其与并列的矩形 2进行优化运算，得矩形 5和矩形6，如图8（b）所示。

五、结语

使用 VC++程序开发语言，通过 ObjectARX接口对AutoCAD系统进行二次开发，是扩展 AutoCAD系统功能的重要手段。本文所提供的算法是在进行转塔冲床辅助设计制造系统的基础上总结出来的图形分析处理方法。在本文的叙述中，针对的是由线段组成的多边形，一般可拆分为矩形和三角形。如果出现更复杂的图形情况，如包含任意内角值的顶点，有圆弧或任意曲线的边，则需要对该算法进行扩展。可首先对特殊边进行处理，再对其两侧的直线段延长，求其交点，便可得到曲线图形和直线段组成的复杂多边形。本算法的目的不是提供万能的算法，而是提供一种解决问题的思路，在实际应用中，还需根据实际情况做相应的处理。IM